基于模糊变系数策略的迎击拦截变结构制导律设计
熊俊辉,唐胜景,郭杰,朱大林
(北京理工大学飞行器动力学与控制教育部重点实验室,北京 100081)
基于模糊变系数策略的迎击拦截变结构制导律设计
熊俊辉,唐胜景,郭杰,朱大林
(北京理工大学飞行器动力学与控制教育部重点实验室,北京 100081)
迎击拦截是拦截问题中常见的一种制导方式。为提高拦截器的末制导精度,基于变结构控制设计零化视线角速率的变结构制导律是一种典型方法。对高速目标的迎击拦截出现相对速度过大,目标机动能力引起的导引初段需用过载过大的问题,应用模糊控制设计制导律的导航项及变结构项系数随剩余导引时间变化的策略以延长系统进入滑模面的时间,使系统进入滑模面的同时有效减小末制导初段的控制量。建模及仿真结果显示,该制导律在使视线角速率收敛的同时显著地减小了导引初段的需用过载,验证了该方法的有效性及对传统比例导引律的优越性。
飞行器控制、导航技术;变结构制导律;模糊控制;迎击拦截;变系数;速度比
0 引言
随着目标飞行器的速度不断增大,拦截器与目标的速度比逐渐减小,甚至出现速度比小于1的情况,如空间轨道飞行器、高超声速再入飞行器的拦截问题,此时传统的尾追式方法已经不能胜任,而迎击拦截成为常见的拦截方法[1-2]。迎击拦截方法虽然对小速度比拦截有理论上的可行性,但其相对速度较大引起的末段视线角速率过早发散及需用过载过大的缺点限制了传统的比例导引律的应用[3],有必要设计新型的制导律。
近年来,基于变结构控制的滑模制导律因其对系统干扰具有较强的鲁棒性获得关注与研究,并在提高末制导精度、消除滑模系统的抖动问题上取得了部分成果[4]。文献[5]提出将变结构制导律应用到拦截问题中,取得很好的效果;文献[6-7]针对空间拦截问题,系统地研究了新型的自寻的导引律,基于变结构控制、最优控制与模糊控制原理设计并改进了末制导导引律,获得一些有益的结论;Moon等[8]设计了基于给定目标机动加速度边界的变结构制导律,无需精确测量目标机动时的加速度,对目标机动及干扰具有较强的鲁棒性;文献[9-11]系统研究了滑模变结构制导律在空间拦截中的应用,并针对轨道飞行器提出前向拦截方法;郭建国等针对大机动目标设计了一种零脱靶量的变结构制导律[12]。Lin等针对速度极高的飞行器研究了分段制导方法,基于显示制导律设计了模糊控制器以使拦截器提前进入目标飞行轨道,并以理想的迎头方式拦截目标[13]。
为实现较小的脱靶量,零化视线角速率的变结构制导律是一种有效方法[4,12]。变结构制导律可视为广义的导航项与变结构项的组合而成,导航项系数类似于比例导引系数,而变结构项系数可以根据目标与系统干扰由自适应规则给出,以满足系统的稳定性要求[6]。如此,在导引初段,视线角速率收敛至0以前的短时间内,较大的导航项与变结构项的控制量叠加会引起需用过载较大的问题,对制导系统不利。针对这个问题,本文在已有研究的基础上,提出模糊变系数策略对其进行改进,以降低导引初段的需用过载。
1 数学模型与问题描述
空间拦截是一个三维目标交会问题,为简化模型方便研究,作以下假设:
1)三维控制问题可以解耦为纵向及侧向平面,本文以纵向平面为例进行研究;
2)将拦截器与目标视为质点;
3)忽略其他系统参数对拦截器与目标的干扰。
迎击拦截(也称迎面拦截),指交会过程中,在视线上拦截器与目标速度具有方向相反的速度分量,直至与目标相遇,如图1所示。
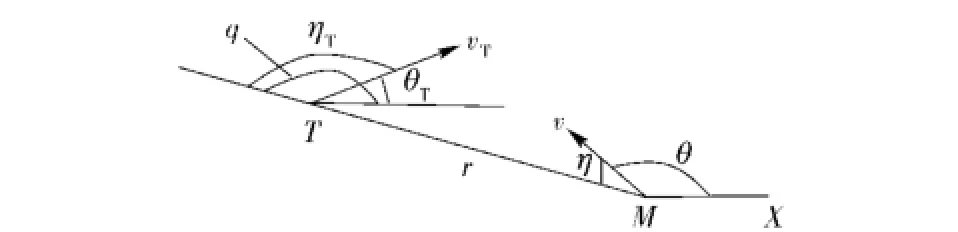
图1 迎击拦截运动关系Fig.1 Sketch of head-on interception
图1中MX为水平基准线,r为拦截器与目标距离,vT、v分别为目标与拦截器的速度,q是目标视线角,η、ηT分别为拦截器与目标速度矢量前置角,θ、θT分别为弹道角及目标航向角。迎击拦截的拦截器、目相对运动方程[14]为

(3)式中:wq、uq物理意义分别为目标加速度和拦截器加速度在视线法向上的分量。
(2)式实质是一个一阶线性时变微分方程。对于直接碰撞的空间拦截问题,要求视线角速率在导引末段接近于0.迎击拦截变结构制导律的设计实际设计uq以零化视线角速率,保证r·<0使拦截器逼近目标的同时降低拦截器的需用过载。
2 制导律设计
2.1 零化视线角速率制导律
根据零化视线角速率设计制导律的思想,选取滑动模态[4]

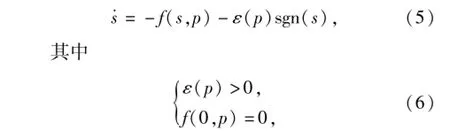
线性时变系统自适应滑模趋近律的一般型表达式可写作(5)式中:f(s,p)是关于s与系统参数p的函数;ε (p)是变结构项系数;sgn(s)是变结构控制的开关函数。
一种常见的趋近律[4]是式中:k、ε为正常数。

文献[4]分析了这样选取的好处:将拦截器与目标的初始距离考虑到趋近速率的设计中,当初始距离较大时可以减小趋近速率;而当接近目标时使趋近迅速增大,使q·收敛,如此可以实现较高的制导精度。
实际中目标机动加速度不可知,设计中把干扰项wq忽略,将(2)式、(4)式代入(7)式得到变结构控制律[2]为若忽略短时间内末段拦截器的速率变化,则由(3)式,可以得到
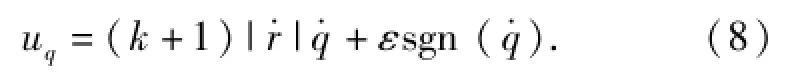

由uq拦截器加速度在视线法向上的分量,又,所以,拦截器的需用过载可近似为

显然,影响拦截器需用过载的参数为uq与η,实际交会过程中η变化较小,且对于高速/高超声速的机动目标,η的初始值并不容易控制。因此,主要通过调节控制量uq值以实现过载分配。
2.2 模糊变系数策略
为了解决上述问题,提出变导航项系数与变结构项系数的策略以改进变结构制导律,取控制律为

式中:k(p)、ε(p)随系统参数变化。该方法的实质是让导引初段的导航项与变结构项的控制量较小,使导引初段拦截器的轨迹较平直以降低需用过载,随着视线角速率逐渐收敛,导引末段的需用过载也较小。令k(p)、ε(p)随导引时间t变化,设计为形如图2所示的线性变化规律,之后达到固定值,即

式中:ts、tf分别为导引开始时刻和结束时刻;δt1、δt2为小的时间段使各系数从初值χ按线性规律变化至ε、k.
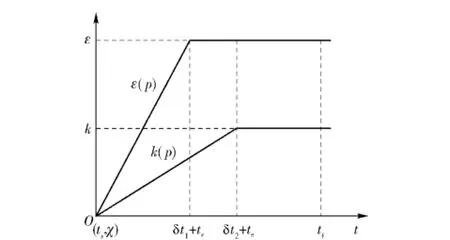
图2 k(p)、ε(p)值变化示意图Fig.2 The variation of k(p)and ε(p)
实现该变系数策略的关键在于,如何获取线性变化时间δt1与δt2.若δt1与δt2取值过小,延缓的效果不佳,不能达到显著降低初段需用过载的目的;若δt1与δt2取值过大,甚至超过剩余导引时间tf-ts值,则会使系统不能到达滑模平面,降低制导精度。
考虑到末制导时间较短,拦截器与目标接近速率变化不大,而且只需要获得大致tf-ts值,所以tf-ts可以用导引初始时刻的距离r(0)与初始相对速度(0)近似得到
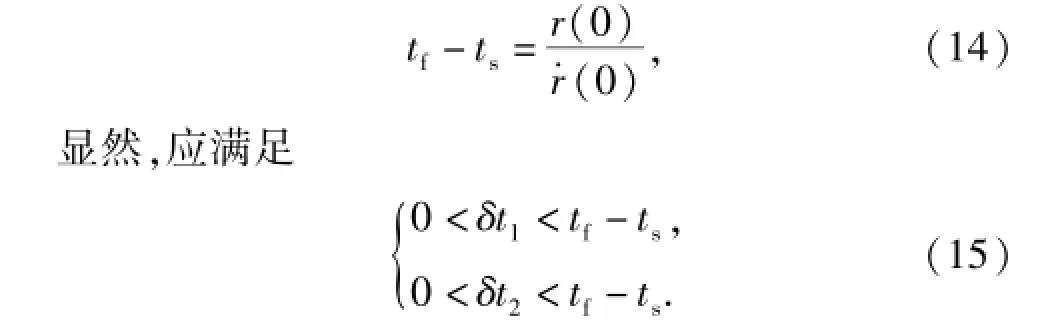
考虑到变系数策略具有一定的主观性,而本文旨在探索这一策略的效果,所以引进模糊控制来实现。为了获得模糊控制规则,先对固定系数的自适应制导律进行大量仿真,得出以下经验:
1)导航项系数与变结构项系数越大,趋近速率越大,q·收敛到0的时间越短;
2)对于高速飞行器的迎击拦截问题(通常Ma数大于3),(8)式制导律收敛至滑模状态约需1~4 s,主要取决于相对速率、趋近率系数等;
3)δt1与δt2取值越大,延缓效果越明显,但q·从初始值到收敛的过渡时间越长。一般情况下δt1与δt2取值为5时具有足够的延缓效果使初段过载减小,根据tf-ts,其范围可为0~5 s.
根据以上经验,应用模糊控制设计δt1与δt2值[14]。把tf-ts作为输入变量,将其乘以量化因子得到模糊化输入变量,模糊子集定义为{0 1 2 3 4 5 6},定义语言输入变量为,论域为{ST MS ME ML LO},其中ST代表短,依次增加,LO代表长。设计中,考虑tf-ts≤18 s,量化因子为1/3,当tf-ts>18 s时可以直接给定δt1与δt2为固定值5.δt1(δt2)为输出变量,语言输出变量为(),论域为{ST MS ME ML},量化因子为1.模糊化输入量与输出量的隶属函数如图3所示。

将(12)式、(13)式、(16)式代入(11)式得到模糊变系数变结构制导律(FASMG)为
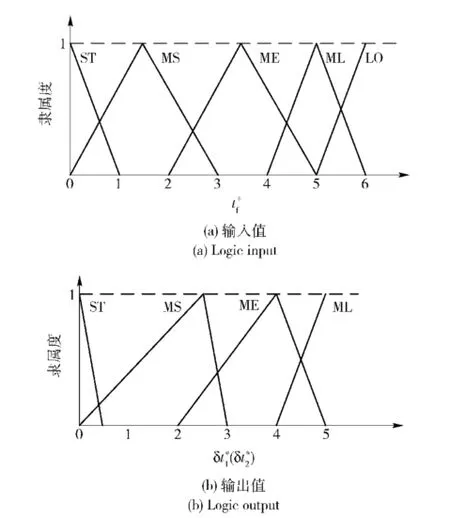
图3 模糊化输入量与输出量隶属函数Fig.3 Membership functions of logic input and logic output

图4 模糊化输入量与输出量关系曲线Fig.4 Graph of logic input and logic output
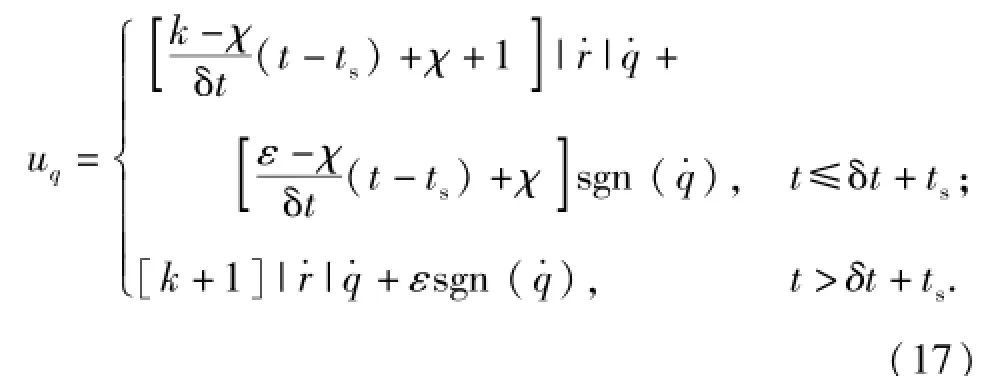
3 仿真及分析
考虑该变结构制导律对迎击拦截的有效性,考虑速度比小于1的高超声速拦截,3种制导律的仿真中给定目标与拦截器的初始条件相同。假定拦截器与目标分别以v=1 360 m/s、vT=1 700 m/s作等速运动,此时速度比为0.8.进入导引段时目标以最大过载10 g作频率为0.25 Hz的正弦机动。设定拦截器、目标运动初始值:r(0)=15 000 m,q(0)= 170°,σT(0)=0°,q(0)=170°,σ(0)=165°.取k= 2,ε=150,χ=0.
基于以上参数,记ts为0,分别采用传统的比例导引律[14](PN)、文献[6]设计的(8)式变结构制导律(ASMG)与本文提出的FASMG进行仿真。
从图5可以看出,3种制导律均能实现与目标的交会,相比于PN,FASMG的末段轨迹更趋于平直;相比ASMG,FASMG初始段更平直。由图6可知,PN的视线角速率受目标机动影响大,且末段趋于发散;ASMG的视线角速率快速进入滑模平面,末段收敛于 0;FASMG在导引初始段有类似于PN的视线角速率,随后类似ASMG迅速进入滑模平面,使末段视线角速率收敛0.
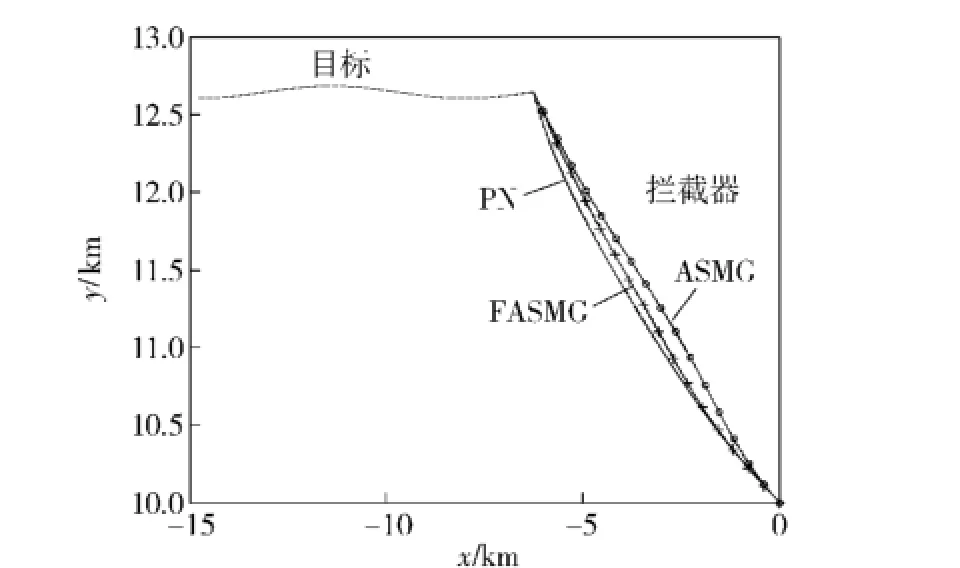
图5 迎击拦截轨迹曲线Fig.5 The trajectory of head-on interception
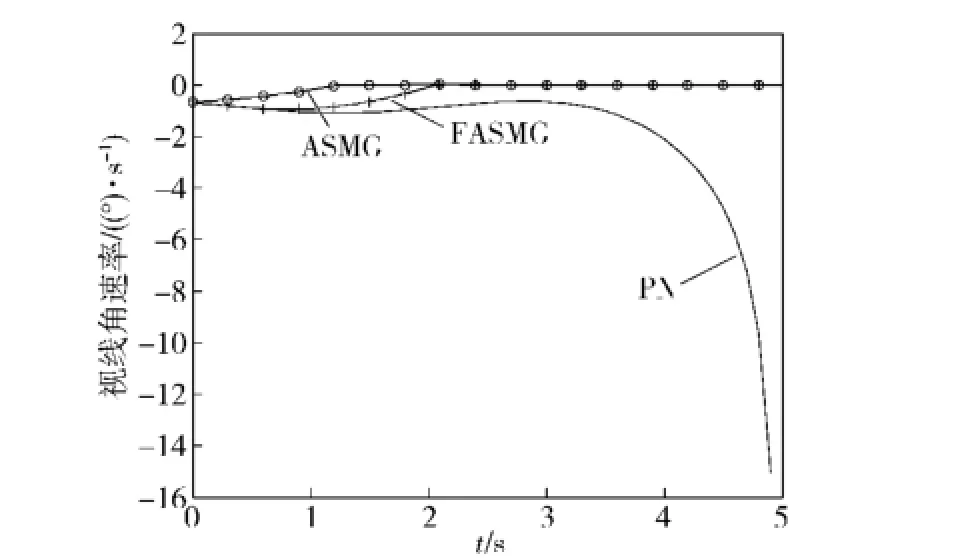
图6 视线角速率比较Fig.6 The comparison of LOS angular rates
从图7所示的过载曲线看出,PN的需用过载初始段较为平均,但末段急剧增加并过早发散,不利于直接碰撞进行拦截;ASMG末段需用过载较小,但初始段过载较大。本文改进的模糊变系数策略除了具有ASMG末段视线角速率收敛的优点外,还明显地减小了导引初始段的需用过载。

图7 需用过载比较Fig.7 The comparison of required overload
4 结论
针对高速飞行器的小速度比的迎击拦截问题,在自适应零化视线角速率变结构制导律的基础上,设计一种模糊控制器实现制导律系数随导引时间变化的规律,延缓系统进入滑模状态的时间以减小导引初段的控制量。通过仿真验证,该制导律的末段视线角速率收敛的同时有效地减小了迎击拦截的导引初始段的需用过载,整个导引段过载分布较均匀。
References)
[1] Prasanna H M,Ghose D.Retro-proportional-navigation:a new guidance law for interception of high-speed targets[J].Journal of Guidance,Control,and Dynamics,2012,35(2):377-386.
[2] 熊俊辉,唐胜景,郭杰.高超声速巡航飞行器防御方案探讨[J].飞航导弹,2012(1):13-15.
XIONG Jun-hui,TANG Sheng-jing,GUO Jie.Discussion on defense methods of hypersonic cruise vehicle[J].Winged Missiles Journal,2012(1):13-15.(in Chinese)
[3] 肖增博,雷虎民,滕江川,等.目标飞行器反拦截协同制导策略[J].兵工学报,2011,32(12):1486-1492.
XIAO Zeng-bo,LEI Hu-min,TENG Jiang-chuan,et al.Cooperative guidance strategy in anti-interception for target aircrafts[J]. Acta Armamentarii,2012,32(12):1486-1492.(in Chinese)
[4] 周荻.寻的导弹新型导引规律[M].北京:国防工业出版社, 2002.
ZHOU Di.New guidance laws for homing missiles[M].Beijing: National Defense Industry Press,2002.(in Chinese)
[5] Brierly S D,Longchamo R.Application of sliding mode control to air-air interception problem[C].IEEE Transactions on Aerospace and Electronic System,1990,26(2):306-324.
[6] Zhou D,Mu C D,Xu W L.Adaptive sliding mode guidance of a homing missile[J].Journal of Guidance,Control,and Dynamics, 1999,22(4):589-594.
[7] Zhou D,Mu C D,Xu W L.Fuzzy adaptive variable structure guidance for space interception[J].Tsinghua Science and Technology,1999,4(4):1610-1614.
[8] Moon J,Kim K,Kim Y.Design of missile guidance law via variable structure control[J].Journal of Guidance,Control,and Dynamics,2001,24(4):659-664.
[9] Shima T,Golan O M.Head pursuit guidance[J].Jounal of Guidance,Control,and Dynamics,2007,30(5):1437-1444.
[10] Golan O M,Shima T.Head pursuit guidance for hypervelocity interception[C]∥AIAA Guidance,Navigation,and Control Conference and Exhibit.Providence,Rhode Island:AIAA, 2004:16-19.
[11] Golan O M,Shima T.Precursor interceptor guidance using the sliding mode approach[C]∥AIAA Guidance,Navigation,and Conference and Exhibit.San Francisco,California:AIAA, 2005:15-18.
[12] 郭建国,周凤岐,周军.基于零脱靶量设计的变结构末制导律[J].宇航学报,2005,26(2):152-156.
GUO Jian-guo,ZHOU Feng-qi,ZHOU Jun.Variable structure terminal guidance law based on zero miss-distance[J].Journal of Astronautics,2005,26(2):152-156.(in Chinese)
[13] Lin C L,Chen Y Y.Design of fuzzy logic guidance law against high-speed target[J].Journal of Guidance,Control,and Dynamics,2000,23(1):17-24.
[14] 钱杏芳,林瑞雄,赵亚男.导弹飞行力学[M].北京:北京理工大学出版社,2006.
QIAN Xing-fang,LIN Rui-xiong,ZHAO Ya-nan.Flight dynamics of missiles[M].Beijing:Beijing Institute of Technology Press,2006.(in Chinese)
[15] 石辛民,郝整清.模糊控制及其MATLAB仿真[M].北京:清华大学出版社,2008.
SHI Xin-min,HAO Zheng-qing.Fuzzy control and MATLAB simulation[M].Beijing:Tsinghua University Press,2008.(in Chinese)
Design of Variable Structure Guidance Law for Head-on Interception Based on Variable Coefficient Strategy
XIONG Jun-hui,TANG Sheng-jing,GUO Jie,ZHU Da-lin
(Key Laboratory of Dynamics and Control of Flight Vehicle,Ministry of Education,
Beijing Institute of Technology,Beijing 100081,China)
Head-on interception is a common guidance method for interception problem.The adaptive variable structure guidance law guiding the line-of-sight angular rate to converge to zero is available to improve the guidance precision.However,the variable structure guidance law leads to large required acceleration of interceptor before the line-of-sight angular rate converges to zero,especially in a situation where the target has strong maneuverability as well as high velocity.A strategy making the coefficients of the guidance law vary according to a typical rule via fuzzy control is proposed.Smaller guidance coefficients are selected at the beginning of terminal guidance.Therefore,the guidance command is reduced and a smaller acceleration of interceptor is incurred.As the coefficients grow to the fixed and desired values, the line-of-sight angular rate converges to zero rapidly so that the stability of the guidance system is guaranteed.It is concluded that the fuzzy variable coefficients strategy is highly effective for head-on interception as shown in the simulation.
control and navigation technology of aerocraft;variable structure guidance law;fuzzy control;head-on interception;variable coefficient;velocity ratio
V448.133
:A
1000-1093(2014)01-0134-06
10.3969/j.issn.1000-1093.2014.01.020
2013-04-19
北京理工大学重大项目培育计划专项(2012CX01007)
熊俊辉(1986—),男,博士研究生。E-mail:xjhwhy@126.com;
唐胜景(1959—),男,教授、博士生导师。E-mail:tangsj@bit.edu.cn

