尾翼稳定脱壳穿甲弹脱壳动力学过程的三维数值模拟

黄振贵,陈志华,郭玉洁

(南京理工大学瞬态物理国家重点实验室,江苏南京 210094）

尾翼稳定脱壳穿甲弹脱壳动力学过程的三维数值模拟

黄振贵,陈志华,郭玉洁

(南京理工大学瞬态物理国家重点实验室,江苏南京 210094）

尾翼稳定脱壳穿甲弹(APFSDS)的脱壳过程对其飞行稳定性与效能具有非常重要的作用。为了描述脱壳过程中卡瓣与弹体之间的气动干扰以及卡瓣相对弹体分离的六自由度(6DOF)运动轨迹,基于流体力学控制方程与外弹道6DOF运动方程,利用动网格技术,对尾翼稳定脱壳穿甲弹弹托在气动力和重力作用下相对弹体分离的三维流场进行了数值模拟,得到了不同分离阶段的流场特性与各卡瓣、弹体气动系数随时间的变化曲线,揭示了弹托分离过程中,卡瓣与弹体之间的激波与气流在不同分离阶段的相互作用过程。耦合6DOF方程计算了各卡瓣的运动轨迹与相应的气动参数,计算结果与文献[15]实验结果相符,表明数值模拟空气动力学与飞行力学相互耦合的控制方程是一种研究尾翼稳定脱壳穿甲弹脱壳动力学过程的新方法。

流体力学;尾翼稳定脱壳穿甲弹;弹托分离;动网格;六自由度;激波

0 引言

尾翼稳定脱壳穿甲弹(APFSDS)通常称为杆式穿甲弹或者动能弹。自20世纪60年代原苏联在115 mm滑膛炮上装备该弹以来,迅速成为各国反坦克火炮装备的主要弹种之一,其外形主要特点是弹体细长,弹径较小,长径比可达到30以上,且具有初速高(Ma≥4.0)、飞行时间短、威力大、防弹跳性能好、后效作用理想等优点[1]。

APFSDS主要由弹体与弹托组成,其中弹体直径远小于弹丸(弹托)直径,弹托在弹丸飞出膛口后受膛内燃气与空气动力作用开始脱离。研究表明,弹托分离过程中弹托和弹体之间的气动力效应将直接影响着弹托能否顺利分离,从而进一步影响弹体的飞行稳定性、射击精度以及穿甲性能等。此外,对弹托在气动力和重力作用下的分离实验不仅成本高,危险大,且难以实现对弹托分离过程的多姿态测量。因此,展开对APFSDS弹托非稳态分离过程的数值研究具有重要的意义。

Heavey等[2]利用Fluent等多种计算流体动力学软件数值模拟了APFSDS刚离开膛口时的固定位置上的二维和三维流场,结果表明Fluent软件对APSFDS超高声速绕流流场具有较强的数值模拟能力。Guillot等[3]基于外弹道方程数值计算了多种IAT弹托分离的弹道轨迹,与采用实验、分析模型得到的弹道吻合得较好。Erengil[4]在文献[3]的基础上提出了一种新的IAT弹托分离弹道模型,该模型不再利用经验公式而是采用理论计算公式计算弹托分离的轨迹,将所得结果与实验数据进行对比,证实该模型具有更强的计算能力。Bhange等[5]基于二维理想气体假设以及6自由度(6DOF)弹道方程对弹托分离和弹体自由飞行的整个过程进行了仿真,获得弹托前端压力分布,且与实验结果基本相吻,并提出了弹托的优化设计原则。

武频等[1,6]应用有限体积TVD格式数值模拟了弹托位于某些特定位置时的二维和三维对称分离流场,表明弹托和弹体之间存在较强的激波反射、交汇。为扩大计算规模、提高计算速度和精度,代淑兰等[7]采用多台计算机并行的方法对APFSDS某特定位置的流场进行了数值模拟。沈坚平等[8]通过建立APFSDS脱壳过程中气动干扰特性的计算公式,对弹托与弹体间的气动干扰进行了分析,证实气动干扰是APFSDS脱壳干扰因素中一个不可忽视的主要因素。李鸿志等[9]用菲涅尔透镜间接阴影系统获得APFSDS弹托分离的系列照片,首次清晰地获得弹托在膛口区附近的分离轨迹。赵润祥等[10]先利用脱壳穿甲弹弹托风洞测力实验,得出了相关的气动力数据,然后根据此数据及弹托的特点,建立微分方程,对脱壳穿甲弹弹托分离轨迹进行了计算,得出的分离规律与相关文献基本吻合。

APFSDS的动态脱壳过程对其整体性能优化具有非常重要的作用,本文结合计算流体力学与外弹道学理论,对APFSDS飞出炮口后的弹托从弹体分离的整个动态过程,以及卡瓣飞行轨迹进行了数值模拟,获得了分离过程的流场特性变化以及3个卡瓣各自相对弹体的6DOF的运动轨迹,为研究APFSDS弹托分离的相关问题提供重要参考。

1 计算方法与数值模型

1.1 控制方程与计算方法

本文采用与文献[11-12]相同的控制方程和计算方法,主要涉及3个重要部分:流场求解、6DOF刚体运动求解以及动网格更新算法。通过求解关于动网格的Euler方程,得到分离过程的每一时刻的流场解,然后沿着表面对压力进行积分求得弹托所受的气动力(矩);6DOF求解算法将已求得的气动力(矩)和彻体力(矩),代入6DOF刚体运动方程,求解出下一时刻弹托的运动学物理量,最后由动网格技术中的弹簧光顺法和局部网格重构法根据新的边界值自动计算出弹托相对弹体移动后的网格节点位置。重复上述步骤,即可对弹托相对弹体的整个分离过程进行数值模拟。此外,在后处理中通过动画可清晰再现弹托的分离过程。流场与6DOF刚体运动方程的耦合求解全过程如图1所示。

图1 数值模拟流程Fig.1 Flow chat of numerical simulation

式中:U=[ρ,ρu,ρv,ρw,E]T;F=[ρu,ρu2+p,ρuv, ρuw,(E+p)u]T;G=[ρv,ρuv,ρv2+p,ρvw,(E+p) v]T;H=[ρw,ρuw,ρvw,ρw2+p,(E+p)w]T.其中ρ为气体密度,u、v、w分别为x、y、z方向的速度分量, E为单位质量气体的总能量,其表达式为

三维非定常Euler方程:

式中r为理想气体绝热指数。理想气体的状态方程为

式中R是通用气体常数。(1)式～(3)式组成封闭方程组。

采用动网格技术求解上述方程组时,需要用到动网格控制方程。对于边界发生移动的任意控制体积V,广义标量φ的通用守恒型积分形式的控制方程可写为

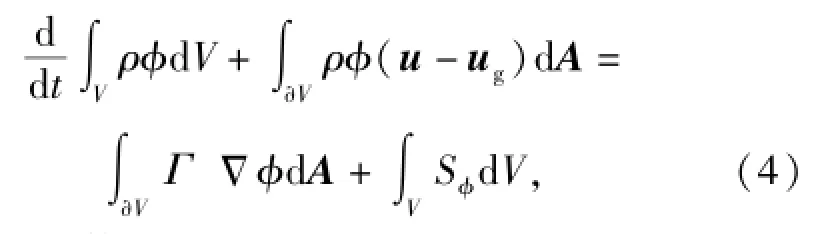
式中:u为流体的速度向量;ug为动网格移动的速度;对于欧拉方程,耗散系数Γ与源项Sφ均为 0;∂V表示控制体积V的边界;A为控制体积面单元向量。

对上述方程的离散,时间项采用基于隐式向后差分格式;空间上基于有限体积法,对流项选用能获得高精度并被广泛采用的迎风格式中二阶隐式AUSM格式,该格式克服了在高马赫数时Roe格式会出现所谓的红宝石现象。运动区域的运动在求得刚体受力(矩)的基础上,通过求解6DOF刚体运动方程来实现。事先指定刚体质心的初始位置和初始运动方向(即初始欧拉角),由动力学方程利用流场的数值模拟结果求得刚体质心运动线(角)加速度,其次根据4阶多点Adams-Moulton公式求解刚体质心的线(角)速度,最后根据运动学方程更新每个时间步长的质心位置和方向。

惯性坐标系下质心平移动力学方程:

而质心的角运动在体坐标系中求解更方便,其动力学方程为

式中:L是刚体的惯量张量;ωB表示刚体在体坐标系下的转动角速度。(6)式和(7)式中的MB、MG分别表示在体坐标系和惯性坐标系下刚体所受到的力矩。(7)式中R表示坐标转换矩阵,其中:Cχ= cos(χ);Sχ=sin(χ);φ、θ、ψ为欧拉角,分别代表以x、y、z为转轴的旋转运动。

联合(5)式～(7)式求出刚体的线(角)加速度后可利用4阶多点Adams-Moulton公式求得刚体的线(角)速度(见(8)式),从而根据刚体的运动学方程即可获得刚体位移以及在空间的姿态。

由于各卡瓣在气动力(矩)和重力(矩)的作用下进行6DOF运动,因此计算域的边界也在不停地改变,故需要采用动网格技术来更新计算域中网格节点位置,使得网格能够适应计算域的变化。本文采用弹簧光顺法和局部网格重划法相结合的动网格技术来更新计算域中的网格节点。

当运动边界的位移相对网格尺寸较小时,此时网格的扭曲率等没有发生严重的恶化,网格质量也未过多下降,可采用弹簧光顺法稍微移动部分网格节点的位置以适应计算域的变化,采用此方法网格拓扑始终不变,无需插值,可保证计算精度;当运动边界的位移相对网格尺寸过大时,变形后的网格会产生较大的倾斜变形,网格质量已恶化并有可能影响计算精度,此时,采用弹簧光顺网格后已无法从根本上改善网格质量,须采用局部网格重划技术,利用插值方法在网格质量不符合要求的计算区域内重新生成质量更好的网格,来适应计算域的较大变化。

1.2 网格生成与数值模型

APFSDS按照弹托形状,主要分为花瓣型和马鞍型两大类。其中弹托一般由2瓣或者更多瓣卡瓣组成,其形状十分复杂,对网格生成造成很大困难。为了方便,本文以3瓣卡瓣为例进行计算。根据先前的二维数值模拟结果对弹丸外形进行适当简化[14],利用三维造型软件建立弹托与弹体的几何模型,如图2所示,其中弹杆主体直径d,弹杆尾部直径1.09d,弹丸长l,弹杆尾部长0.232l,弹杆圆柱部长0.605l,弹头长度为0.163l;卡瓣长0.416l,最大径向长3.55d,卡瓣内壁面与弹杆圆柱部的初始径向距离为0.182d,卡瓣最前端距离弹尖0.291l;尾翼高2.05d,厚0.09d,底部长0.180l,顶部长0.044l.然后,建立外流场计算域并进行四面体非结构化网格划分,网格数量约为800万,并为了提高求解精度对弹丸周围部分区域加密。图3为弹丸和卡瓣表面网格分布图。通过多次试算,取计算域半径为36.36d,长为1.560l的圆柱体,弹头尖点离圆柱顶面的距离为0.096l,弹丸尾端点距离圆柱底面0.464l.

图2 APFSDS几何模型Fig.2 APFSDS geometric model

图3 弹丸和卡瓣表面网格分布图Fig.3 Surface meshes of projectile and sabot

对于边界条件的设定,物面边界采用绝热壁面;计算域外边界为压力远场边界条件,压力为一个标准大气压,温度为300 K.假设来流Ma为4.0,攻角为0°.

弹托分离受到诸多因素影响,且非常复杂,如在出膛口瞬间分离时,会受到膛口燃气流与冲击波的影响,对脱壳瞬间各卡瓣和弹体运动的初始条件与初始脱壳不对称性等有影响。为了简便,本计算对此暂不考虑,并将参考系建在弹体上,弹托在气动力和重力作用下相对于弹体从静止开始发生6DOF运动。初始欧拉角的设置如表1所示。

表1 各卡瓣的初始欧拉角Tab.1 Initial Euler angles of three sabots

2 结果与讨论

2.1 不同时刻的流场分析

图4～图6分别为用x-y剖面压力等势分布表达的弹托从弹体表面脱离的初始、中间以及弱耦合与自由飞行过程。它们分别代表了弹托在分离过程中几个具有显著特征的特定流场。

为了方便,将图4～图6中弹体上方的卡瓣命名为sabot_1,弹体右侧面即剖面背面的卡瓣为sabot_2,弹体左侧是卡瓣sabot_3.初始时刻,图中剖面恰好位于sabot_1和弹体轴对称面上,并穿过sabot_2与sabot_3之间的狭小缝隙。本小节主要以sabot_1为例讨论弹托分离过程中的流场变化及其与激波的相互作用过程(如交汇作用与反射等),故若没有特指,所说的卡瓣为sabot_1.

弹托初始分离时,由图4可知,由于为超声速运动,弹体头部有斜激波,同时弹托前缘(前腔)为高压区,且该高压区会保持较长时间(见图4与图5),因此在弹托前形成脱体激波(见图4(a))。随着各卡瓣的受力不同,它们开始与弹体产生分离,导致脱体激波变形,且沿弹体向尾部延伸并与弹体发生碰撞,造成此处弹体表面压力的急剧升高(见图4(b))。卡瓣前腔的高压不仅为卡瓣的分离提供了轴向力与径向力,而且为卡瓣的俯仰运动提供了力矩。另外,卡瓣表面其他凸起处同样会有斜激波,并在其表面产生高压区,这为其分离同样提供力(矩)。

卡瓣初始分离过程中,高速气流在绕过卡瓣过程中主要分成三部分:在卡瓣前腔下部转弯处发生膨胀的气流,会折转到与卡瓣内表面平行,并从卡瓣与弹体之间的间隙流向弹尾;在卡瓣前腔上部的部分气流在越过卡瓣上方后向卡瓣尾部流动并形成膨胀波;最后一部分气流则从各卡瓣相互之间的间隙穿过,由于此时的各间隙极小,因而极易导致壅塞的出现,并使弹体和卡瓣表面对应区域的压力增加,其最高压力值会随着间隙的增大而迅速减小。而气流在穿过此处的喉状激波后压力迅速下降(如图4(c)所示);当间隙足够大时,喉状激波将会与脱体激波融合在一起(如图5(a)所示),此时弹托将要进入中间分离过程。

图4 初始分离过程时的x-y剖面压力等势分布Fig.4 Pressure distribution of x-y section during initial separating

图5 中间分离过程时的x-y剖面压力等势分布Fig.5 Pressure distribution of x-y section during middle separating

弹托分离的中间过程中,脱体激波转变为作用在卡瓣上的斜激波,且靠近弹体一侧的斜激波与弹体碰撞强度随着弹体和卡瓣间隙增加而降低。

图5(a)中可清晰地显示到斜激波与弹体碰撞形成反射激波。一定条件下,反射激波与卡瓣内表面再次发生碰撞并反射(见图5(b)),这样导致弹体与卡瓣之间有多道反射激波,并使其对应面压力增大,从而为卡瓣的顺利分离提供了额外径向分力,并对弹体的飞行稳定性产生一定的影响。

另外,卡瓣分离过程的俯仰运动会使卡瓣尾部在某些时候与弹体的径向距离不是很大,这时一道喉状激波会出现在卡瓣尾部下方区域,但其强度要比卡瓣前腔的脱体激波弱,并随着径向距离的增大而消失(见图5(c)).

当卡瓣和弹身之间的距离足够大时,它们之间的气动干扰几乎消失,弹托分离过程进入弱耦合和自由飞行过程,此时由于卡瓣经翻转,其内表面变成迎风面(如图6(a)所示),因而其气动阻力会大大增加,在翻转的同时会迅速向弹体尾部运动,其表面所形成的激波可能会与弹体尾部进行碰撞,对弹体产生翻转力矩(如图6(a)和图6(b)所示)。

t=4.5 ms时(见图6(c)),激波已完全离开尾翼,各卡瓣和弹体之间干扰随之消失,卡瓣和弹体各自作自由飞行运动。

上述结果表明,弹托分离过程中,各卡瓣和弹体的流场结构以及激波的相互耦合作用,是卡瓣分离过程中的气动力来源,表明了卡瓣与弹体之间的流场非常复杂且存在着强气动干扰。虽然对其分离过程人为划分了3个阶段,但各个阶段相辅相成,并影响其最终分离结果。图7为实验所得的流场波系结构与弹托分离轨迹[15]。图7(a)是某时刻弹托分离的流场实验图,可清晰地看到弹托前存在斜激波,并且激波尾部刚好扫到弹体,此外在弹托表面的某些凸起处也产生了斜激波,并对后方流场产生影响。这些特征同样地展示在本文的数值模拟结果中(如图4和图5所示),这说明本文数值方法在描述流场特征上的有效性。

图6 弱耦合与自由飞行过程x-y剖面压力等势分布Fig.6 Pressure distribution of x-y section during weak coupling and free flying

2.2 卡瓣的6 DOF运动

图8为3个卡瓣分别在4个不同时刻与弹体的相对分离位置与姿态。由图8可知,sabot_1以俯仰和轴向运动为主,而其余2个卡瓣除此之外,侧向运动和翻转运动同样也很明显,导致各卡瓣姿态的变化不一样。这些姿态变化充分体现了弹托分离过程中所受空气动力作用的非对称性。图7(b)为应用图像识别和处理技术对实验正交阴影照片处理得到的卡瓣相对弹体的分离轨迹。由图7(b)可知,其与图8(a)基本相同,因此也验证了本文的数值方法对卡瓣飞离轨迹捕捉的有效性。

以各卡瓣相对于分离前的径向和轴向距离为例来讨论卡瓣在重力和气动力作用下的6DOF刚体运动。图9与图10分别为3个卡瓣重心径向与轴向距离随时间的变化趋势。由图9可知,3个卡瓣在气动力和重力作用下逐渐远离弹体,其变化趋势基本为直线,意谓着各卡瓣基本以匀速径向远离弹体。但sabot_1远离弹体的速度要比其他2个卡瓣稍慢。径向距离在卡瓣初始分离时间段内(0.3 ms左右)几乎相等。随着卡瓣的继续分离,sabot_1的径向距离逐渐表现出与其余两个卡瓣的差异性,而sabot_2与sabot_3的径向距离直到3 ms后才表现出稍微的不同。

从图10可知,各卡瓣轴向运动距离变化梯度随时间变化加大,说明卡瓣以加速度相对弹体向后运动,从而使卡瓣轴向移动速度增加。但各卡瓣轴向距离的差异性没有径向距离大,直到1.5 ms后, sa-bot_1的轴向距离逐渐小于其他2个卡瓣,但sabot_2与sabot_3的轴向距离却早于径向距离出现差异性。总的来说,3个卡瓣的径向和轴向距离均相差不大,但它们在空间中的姿态却极其不相同(如图8所示)。

2.3 气动系数的分析与讨论

图11为各卡瓣在分离过程中阻力系数Cd的变化情况。初始阶段时,3个卡瓣的阻力系数大小与变化趋势几乎相等,这表明分离开始阶段,各卡瓣相对弹体的轴向距离几乎相同,并能防止卡瓣向后移动过快而与尾翼、弹芯等发生碰撞,确保卡瓣顺利分离。阻力系数下降到一定程度后慢慢回升,并随着其姿态的变化而产生振动。sabot_1因其滚转较慢从而使其阻力系数开始时较小,直到t=2.0 ms后,迅速上升并超过其余2个卡瓣的阻力系数。在t= 4.1 ms左右,sabot_1的内表面刚好正对着来流(见图6(b)),造成阻力系数达到最高值。此后由于卡瓣继续向后翻转造成正对气流的面积逐渐减小,阻力系数随之迅速下降。sabot_2与sabot_3的阻力系数在达到第2个谷值后逐步上升,但sabot_2的阻力系数更早达到峰值,峰值也小得多,下降后也更早达到谷值,但是达到最高值却比sabot_3稍微早一些。sabot_2的阻力系数曲线先是比sabot_3平稳得多,再慢慢变得比较陡峭,这说明sabot_2姿态变换先是比sabot_3平稳,后变得陡峭。这些变化可在图8中得到验证。

图7 实验得到的流场波系结构图和弹托相对弹体的分离轨迹图[15]Fig.7 Shock wave structure of flow field and sabot discarding trajectory from experiment in Ref.[15]

图12为弹托升力系数Cl随时间的变化曲线图。由于升力系数以正Y轴为正方向,故图中的升力系数有正负之分。这里以sabot_1为例来分析升力系数,在分离的初始时刻,升力系数急剧上升,之后在较长一段时间内呈现出振幅不大的震荡,并在t=1.1 ms左右时再次出现峰值,这与在图5(b)中反射激波碰撞卡瓣内表面相符,而在t=1.7 ms时下降到谷值,这是因为卡瓣尾部的喉状激波在此时已消失。在此之后,由于卡瓣俯仰到一定角度脱体激波开始延伸到卡瓣内表面(见图6(a)),升力系数在较长时间段内保持上升的态势,而当卡瓣俯仰过大时,卡瓣内表面在Y方向的投影开始变小,从而造成升力系数逐渐减小,并在t=4.0 ms左右,变为0,升力开始改变方向,并沿着新方向逐渐增大,这说明在分离的最后阶段,重力的作用逐渐大于气动力,卡瓣在Y方向上做减速运动,若飞行时间足够长,该卡瓣最终会在重力的作用下,掉落到地面。各卡瓣升、阻力系数随着时间不断起伏,主要由卡瓣在不同时刻的姿态变化导致其受空气动力作用不同所致。而这又与它们各自的初始欧拉角相关,欧拉角表征卡瓣分离过程的姿态变化,并最终导致其气动力,分离姿态与轨迹变化。因此,sabot_2与sabot_3的升、阻力系数随时间的变化在卡瓣分离一段时间后有不同变化趋势,且其轴向速度与径向速度也因受力的不同而有不同变化趋势,最终导致轴向距离与径向距离各不相同(见图9和图10)。

图8 卡瓣分离过程图Fig.8 Discarding processes of sabots

图9 卡瓣重心的径向距离随时间的变化曲线Fig.9 Time-dependent curves of radial displacements of gravity centers of sabots

图10 卡瓣重心的轴向距离与时间的关系Fig.10 Time dependent curves of axial displacements of gravity centers of sabots

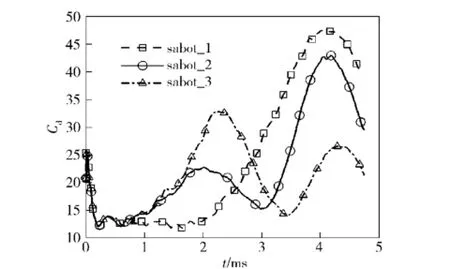
图11 弹托阻力系数随时间的变化关系Fig.11 Sabot drag coefficient vs.time

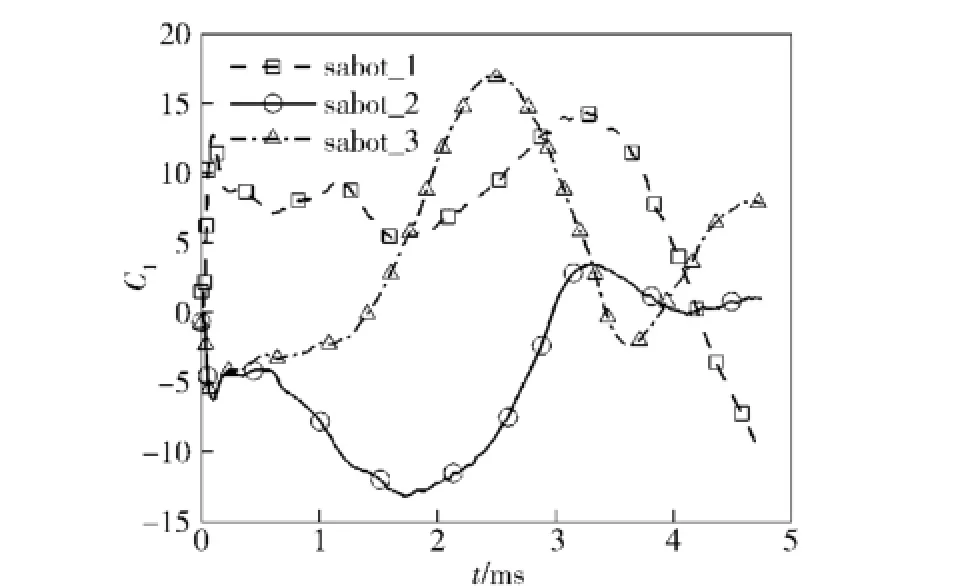
图12 弹托升力系数随时间的变化关系Fig.12 Sabots lift coefficient vs.time

图13为弹体分离过程中的气动力与力矩系数Cd、Cl、CZ、CMX、CMY、CMZ随时间的变化曲线。由图13可知,气动力系数和相应的力矩系数均在相同时刻出现极值。如升力系数从t=2.9 ms时开始出现负的极值点(见图13(b)),对照图6(a)可知,此时卡瓣sabot_1的尾部斜激波刚好与弹体尾部相碰,导致弹体尾部上表面碰撞区域的压力剧增,因而压力系数下降到极值。而由于其他2个卡瓣的斜激波对弹体的作用较小,因而此时的俯仰力矩系数主要受升力影响同样上升到极值。它们在达到极值后仍保留了一定的时间,这说明卡瓣sabot_1分离时的尾部斜激波在弹体尾部同样有停留,这同样可从图6(b)可知。而在t≤2.9 ms的各力与力矩的脉动,同样由3个卡瓣分离过程中各自的斜激波与弹体相互作用引起。而在t≥4.5 ms以后,卡瓣对弹体影响基本结束,弹体各力与力矩系数相对平稳。

图13 弹体气动系数与时间的关系曲线Fig.13 Aerodynamic coefficients of projectile vs.time

3 结论

本文基于流体动力学与外弹道学控制方程,利用计算流体力学数值计算方法与动网格技术对APFSDS的弹托动态分离过程进行了数值研究。数值模拟结果得到了各卡瓣相对弹体分离的6DOF轨迹,描述了弹托分离过程中流场与各卡瓣姿态,讨论了卡瓣与弹体的气动力(矩)系数随时间的变化,并与相应实验结果一致。

研究表明,卡瓣分离初始阶段,弹体与卡瓣之间产生强耦合作用,会形成通气道并产生壅塞与激波的多次反射。卡瓣初始扰动对其气动力变化有重要影响,并进一步影响其姿态。而卡瓣姿态反过来又影响着流场以及激波的分布,并进一步影响卡瓣气动力。

在弹托分离的后期,卡瓣与弹体之间的相互作用降低,卡瓣的轴向与径向距离增加,开始自由运动。各卡瓣的运动轨迹与姿态受其气动力影响而呈现不同运动特点。

弹托分离过程中,会受卡瓣表面的斜激波影响而出现气动力与力矩系数的脉动,特别是斜激波作用在弹尾时所产生的脉动会加剧,并极易导致弹体失稳。

References)

[1] 武频,尚伟烈,赵润祥,等.APFSDS弹托分离干扰三维流场数值模拟[J].空气动力学学报,2005,23(1):1-4.

WU Pin,SHANG Wei-lie,ZHAO Run-xiang,et al.Three dimension numerical simulation for APFSDS sabots separating and discarding flow field[J].ACTA Aerodynamica Sinica,2005, 23(1):1-4.(in Chinese)

[2] Heavey K R,Despirito J,Sahu J.Computational fluid dynamics flow field solutions for a kinetic energy(KE)projectile with sabot [R].US:US Army Research Laboratory Aberdeen Proving Ground MD,2003.

[3] Guillot M J,Reinecke W G.A numerical and experimental investigation of sabot separation dynamics[C]∥AIAA 34th Aerospce Sciences Meeting and Exhibit.Reno,NV:AIAA,1996:455.

[4] Erengil M E.Sabot discard model for conventional and electromagnetic launch packages[C]∥19th International Symposium of Ballistics.Interlaken,Switzerland May:International Ballistics Committee,2001:213-215.

[5] Bhange N P,Sen A,Ghosh A K.Technique to improve precision of kinetic energy projectiles through motion study[C]∥AIAA Atmospheric Flight Mechanics Conference.Chicago,Illinois:AIAA, 2009:5270.

[6] 武频,赵润祥,郭锡福.脱壳穿甲弹弹托分离二维数值模拟[J].弹箭与制导学报,2001,21(2):27-29.

WU Pin,ZHAO Run-xiang,GUO Xi-fu.Two dimension numerical simulation of APFSDS sabots discarding[J].Journal of Projectiles,Rockets,Missiles and Guidance,2001,21(2):27-29.(in Chinese)

[7] 代淑兰,许厚谦,王兵.并行计算在脱壳穿甲弹流场三维数值模拟中的应用[J].弹道学报,2007,19(2):85-87.

DAI Shu-lan,XU Hou-qian,WANG Bing.Three-dimensional numerical simulation of APFSDS projectile flow field using parallel computation method[J].Journal of Ballistics,2007,19(2):85 -87.(in Chinese)

[8] 沈坚平,杨启仁,徐明友,等.APFSDS脱壳过程中气动干扰分析[J].弹道学报,1996,8(2):39-43.

SHEN Jian-ping,YANG Qi-ren,XU Ming-you,et al.Analysis of dynamic interference during discarding sabot of APFSDS[J]. Journal of Ballistics,1996,8(2):39-43.(in Chinese)

[9] 李鸿志,崔东明,何正求,等.尾翼脱壳穿甲弹近炮口区飞行姿态的显示[J].兵工学报,1992,13(1):66-69.

LI Hong-zhi,CUI Dong-ming,HE Zheng-qiu,et al.Visualization of flight attitude of a fin-stabilized sabot discard projectile near the muzzle[J].Acta Armamentarii,1992,13(1):66-69.(in Chinese)

[10] 赵润祥,武频,王福华,等.弹托风洞测力试验及其分离规律计算[J].南京理工大学学报:自然科学版,2001,25(6): 579-583. ZHAO Run-xiang,WU Pin,WANG Fu-hua,et al.Force measurement experiment of sabots with wind tunnel and the calculation of its discarding rules[J].Journal of Nanjing University of Science and Technology:Natural Science,2001,25(6):579-583.(in Chinese)

[11] Snyder D O,Koutsavdis E K,Anttonen J S R.Transonic store separation using unstructured CFD with dynamic meshing[C]∥33rd AIAA Fluid Dynamics Conference and Exhibit.Orlando, Florida:AIAA,2003:2013-3919.

[12] Panagiotopoulos E E,Kyparissis S D.CFD transonic store separation trajectory predictions with comparison to wind tunnel investigations[J].International Journal of Engineering,2010,3(6): 538-553.

[13] 姜毅,郝继光,傅德彬.导弹发射过程三维非定常数值模拟[J].兵工学报,2008,29(8):911-915.

JIANG Yi,HAO Ji-guang,FU De-bin.3D unsteady numerical simulation of missile launching[J].Acta Armamentarii,2008, 29(8):911-915.(in Chinese)

[14] 钱吉胜,韩珺礼,黄振贵,等.超声速脱壳穿甲弹二维流场的数值模拟[J].四川兵工学报,2011,32(10):30-32.

QIAN Ji-sheng,HAN Jun-li,HUANG Zhen-gui,et al.Numerical simulation of two-dimension flow field for armor-piercing bullet of supersonic speed deshelling[J].Journal of Sichuan Ordnance,2011,32(10):30-32.(in Chinese)

[15] 杨启仁,徐直军.脱壳动力学[M].第4版.北京:国防工业出版社,1996:264.

YANG Qi-ren,XU Zhi-jun.Dynamic of sabot discard[M].4th ed.Beijing:National Defense Industry Press,1996:264.(in Chinese)

Numerical Simulation on Three-dimensional Dynamic Process of Sabot Discarding of APFSDS

HUANG Zhen-gui,CHEN Zhi-hua,GUO Yu-jie
(Key Laboratory of Transient Physics,Nanjing University of Science and Technology,Nanjing 210094,Jiangsu,China)

The discarding process of armour piercing fin-stabilized discarding sabot(APFSDS)is crucial for its flight stability and lethality.In order to describe the aerodynamic interferences between the projectile and the sabots and the six degree-of-freedom(6DOF)flight trajectories of three sabots with respect to the projectile,the three-dimensional flow field of APFSDS under the action of aerodynamic force and gravity is simulated with the use of the dynamic mesh technique.Based on the governing equations of fluid dynamics and rigid body motion equations of 6 DOF and the variation of flow characteristics during discarding processes and the time history of aerodynamic coefficients of all sabots and projectile are obtained.The interaction process of shock wave and flow between the sabots and the projectile is revealed. Moreover,the trajectories and aerodynamic coefficients of all sabots are also calculated with the coupling 6 DOF equations.which agree well with the corresponding experimental results.The result shows that the numerical solution of the governing equations of aerodynamics and flight mechanics is a new method to study the discarding processes of APFSDS.

fluid mechanics;armour piercing fin stabilized discarding sabot;discarding sabot;dynamic mesh;6 degree-of-freedom;shock wave

TJ413+.2

:A

1000-1093(2014)01-0009-09

10.3969/j.issn.1000-1093.2014.01.002

2013-01-28

国家重点实验室基金项目(9140C300205110C30)

黄振贵(1986—),男,博士研究生。E-mail:hzgui126@126.com;陈志华(1967—),男,教授,博士生导师。E-mail:chenzh@mail.njust.edu.cn