一种度量不确定环境中被动声纳作用距离的计算方法

程广利，张明敏

(海军工程大学 电子工程学院，湖北 武汉430033)

0 引言

被动声纳的作用距离是其重要技术性能指标，也是决定潜艇在反潜作战中能否夺取制胜权的重要要素之一。通常是基于声纳方程来估计被动声纳的作用距离［1］，如:将常见的优质因数(FOM)当成被动声纳的距离指示。实际上，海洋环境严重影响被动声纳的作用距离，因而同一部声纳在不同海洋环境中，作用距离可能相差数倍。我国近海大都是浅海，受到多种环境因素的影响，海洋环境参数具有较强的不确定性［2］，对声传播影响很大，自然影响被动声纳作用距离的预估，从而影响指挥员的战术决策［3］。因此，在不确定海洋环境中如何预报被动声纳的作用距离值得研究。

文献［4］最早考虑被动声纳作用距离的不确定性问题，该方法(简称“方法1”)从声纳方程出发，利用传播模型计算得到不同距离上的传播损失(TL)，代入检测概率方程，求得在每个距离上的检测概率，然后在整个距离上对检测概率积分，获得“探测半径”，认为它是此时被动声纳的“作用距离”。从本质上说，方法1 是对声纳作用距离的一阶原点矩估计，优点在于估计过程简便、直观，不足是由于它利用了矩估计方法，在某些情况下，如:当不确定环境参数ξ 满足Cauchy 分布时不存在原点矩［6］，此时方法失效;而且方法1 没有充分利用ξ 的概率密度函数(PDF)信息获得被动声纳作用距离的概率分布。

文献［5］在文献［4］的基础上，提出并定义了“概率D 条件下的可靠作用距离指标rD”，该方法(简称“方法2”)中，当D=1 时相当于取所有“某次实现的声纳作用距离rmax”中的最小值。从本质上说，方法2 是在方法1 的基础上，通过选用阈值D 的大小来控制“可靠作用距离rD”，优点是参数D 对rD的控制简便、易行;但D 越大，对rD的估计越保守，易产生漏报;D 越小，则rD取值越大，易产生虚警。因此，方法2 的不足是无法确定定量选取D 的准则，只能依赖经验人为决定。

值得说明的是，在不确定海洋环境中声纳的“作用距离”并非是指此时声纳的实际作用距离，只是声纳在此环境条件下对声传播距离覆盖范围的一种度量［4］。文献［4］称之为“探测半径”，文献［5］称之为“可靠作用距离”，本文统称之为“作用距离”。

针对方法1、方法2 的不足，本文在方法1 的基础上，基于极大似然准则，提出一种度量被动声纳作用距离的计算方法，推导了单个和多个(以2 个参数为例)海洋环境参数不确定情况下估计被动声纳作用距离的过程，分析了方法的特性，给出了算例。

1 基本理论

预估不确定海洋环境中被动声纳作用距离的基本方法仍是利用声纳方程，此时的被动声纳方程为

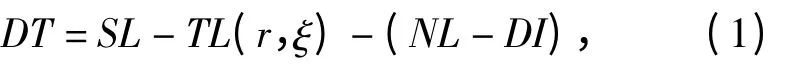
式中:DT 为检测阈;SL 为目标声源级;TL(r，ξ)为考虑不确定性时不同距离r 上的声传播损失;NL 为背景噪声级;DI 为接收阵指向性指数。

(1)式还可表示成FOM 形式，

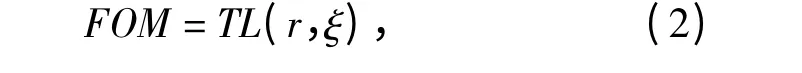
式中:FOM=SL+DI-DT-NL.

则信号余量

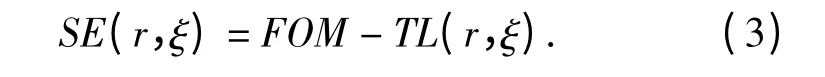
考虑声场中存在服从某种概率分布(如正态分布)的环境参数，对应的检测概率

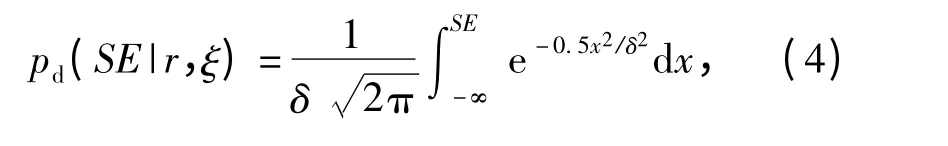
式中:δ 与给定距离r 处的信号检测性能有关，反映了检测区域和非检测区域之间过渡的快慢。

某次实现的声纳作用距离［4］

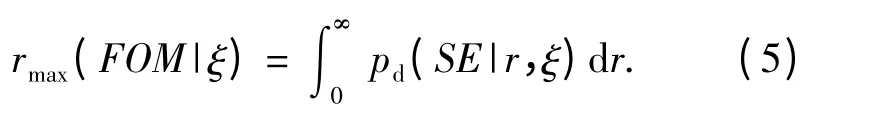
将(4)式代入到(5)式中，得

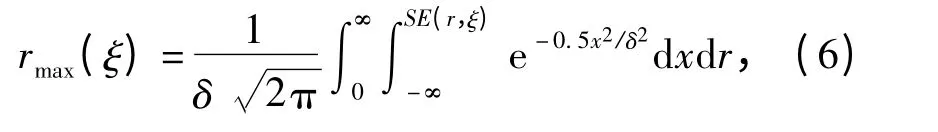
可知rmax(ξ)也是一个不确定量，一般不易直接求得其解析表达式，但可求其近似数值解。rmax在ξ 的不确定性传递作用下必然也呈现出一定的概率分布，按照极大似然准则［6］，其中最大概率密度值对应的rmax就是极大似然估计值rMLE，即为此时被动声纳作用距离的估计值。

1.1 单个海洋环境参数不确定

如果rmax(ξ)严格单调且可微分，令单参数ξ 的概率分布为p(ξ)，则rmax的概率分布为

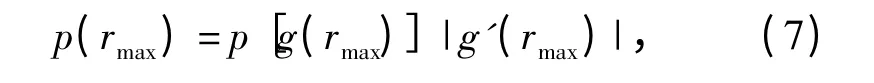
式中:g(rmax)为rmax(ξ)的反函数，即ξ = g(rmax);|·|表示取绝对值。

若rmax(ξ)并非严格单调，将rmax(ξ)分段为N个区间，在这些区间内分别满足单调可微分，则rmax的概率分布可表示为

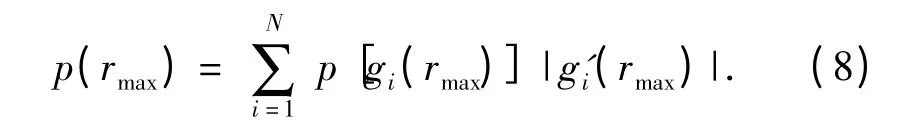
求解获得p(rmax)最大值对应的距离，即为此时被动声纳的作用距离rMLE，其数学求解式为

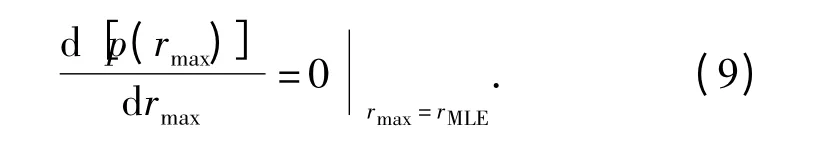
1.2 多个海洋环境参数不确定

以两个海洋环境参数不确定为例，研究度量多海洋环境参数不确定时被动声纳作用距离的极大似然估计法。

假设有两个环境参数ε、η 不确定，二维随机变量(ε，η)的联合概率密度为p(ε，η)，当两个随机变量相互独立时(海洋环境参数通常可满足)，p(ε，η)=p(ε)p(η)，其中p(ε)、p(η)分别为ε、η 的PDF.

定义(ε，η)的变换(u，v)，其表达式为

且存在逆变换

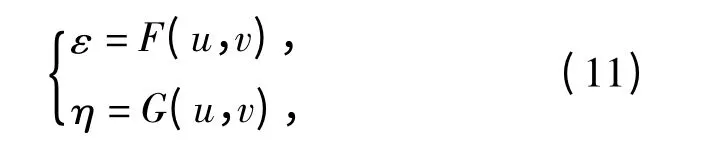
则(u，v)的PDF 可表示为

式中:|J|为Jacobi 行列式，具体表达式为

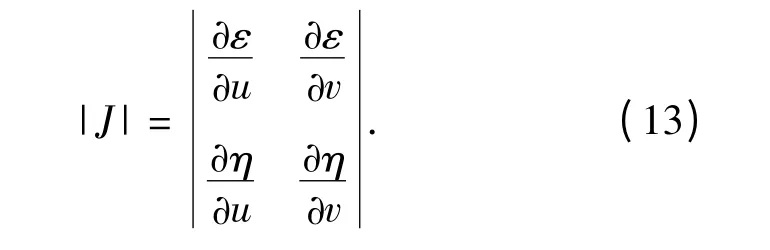
rmax与环境参数(ε，η)之间存在映射关系，因此可将二维随机变量(rmax，η)视为(ε，η)的变换，即令(10)式中u=rmax，v=η，则(rmax，η)的PDF 为

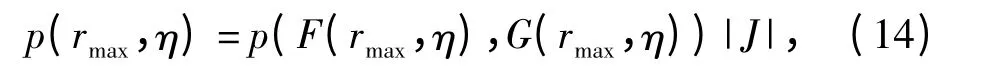
式中:

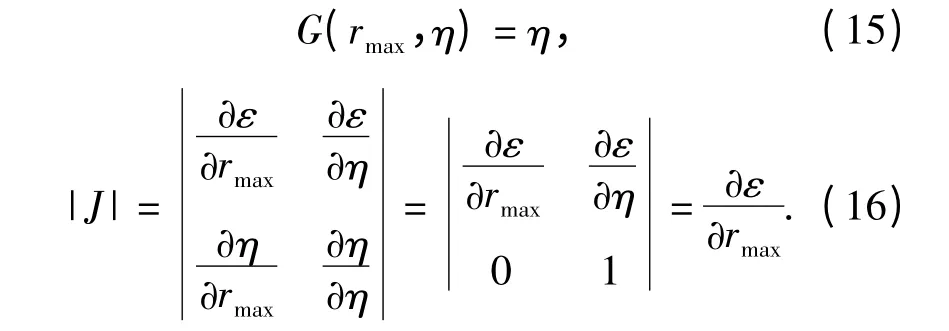
将(14)式对η 积分，得到rmax的概率分布

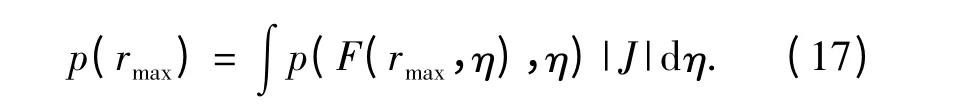
同样，求解p(rmax)取最大值时对应的rmax，即为此时被动声纳的作用距离，2 个以上海洋环境参数不确定时可参照此过程计算。

2 仿真实验与分析

2.1 单个海洋环境参数不确定

图1所示为浅海环境Benchmark 模型。仿真条件:设海面是声压自由边界，海深H =80 m，海底是半无限空间，海底参数c3=1 697 m/s，ρ3=1 866 kg/m3，α3=0.673 dB/λ;声源深度为30 m，声波频率为400 Hz;接收深度为50 m;设温跃层下限深度d2是不确定的，且服从均值为35 m、标准差为2 m的正态分布，c1=1 550 m/s，d1=20 m，c2=1 500 m/s;FOM =75 dB;声纳作用距离的搜索范围为1 ～50 km;声场计算模型为KRAKEN［7］。

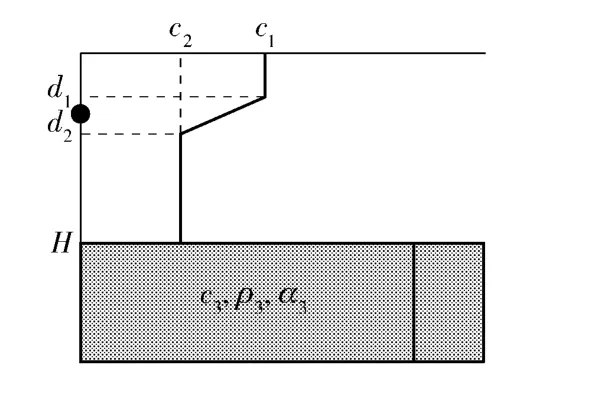
图1 浅海环境Benchmark 模型Fig.1 Benchmark model of shallow water environment

仿真产生10 000 个服从均值为35 m、标准差为2 m 的正态分布d2值，用声场计算模型计算PL，如图2所示。

当接收距离为30 km 时TL 的概率分布如图3所示，可知在浅海环境中考虑了参数的不确定性时，在某个接收距离上TL 不再是一个确定值，而是满足一定概率分布的不确定量，为声纳的作用距离估计带来不确定性，同时从图3可知此时TL 已不再服从正态分布，这也充分说明海水中的声传播是一个典型的非线性过程。

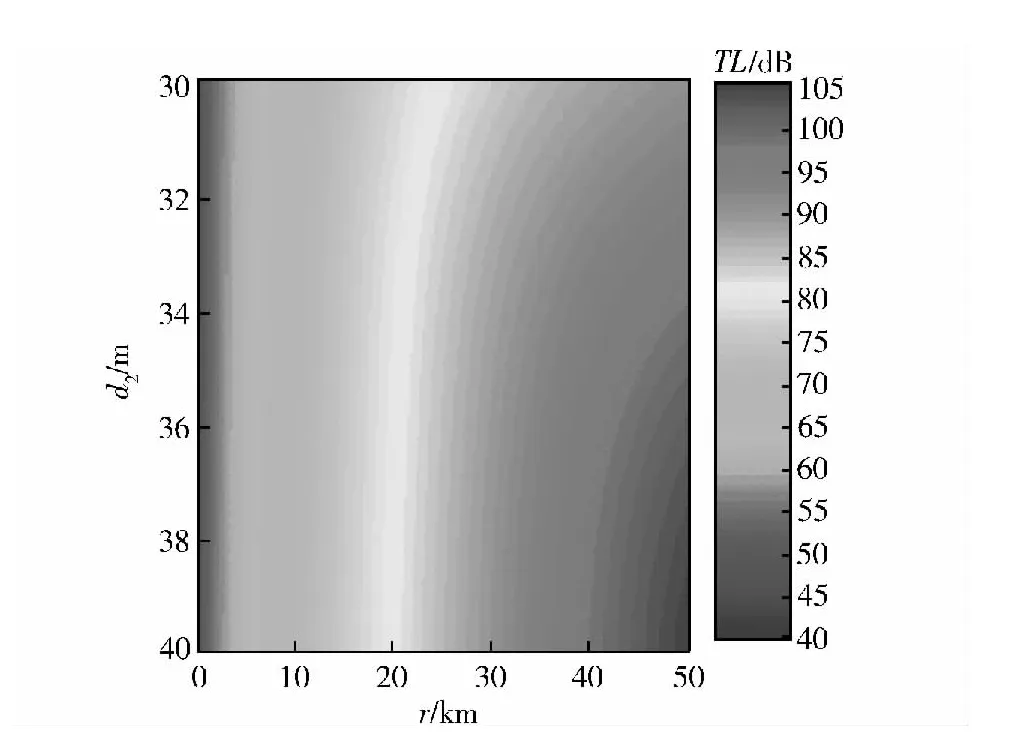
图2 d2不确定范围内的声传播损失Fig.2 Transmission loss within uncertain range of d2

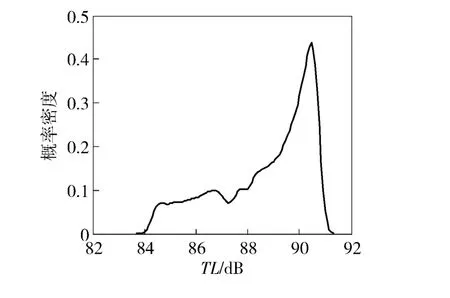
图3 接收距离为30 km 时声传播损失的概率分布Fig.3 PDF of transmission loss at the receiving range of 30 km

采用最小二乘法，拟合不确定环境参数d2与rmax之间关系表达式的曲线如图4，由图4可知二者一致性很高，拟合曲线即g(rmax)的表达式为

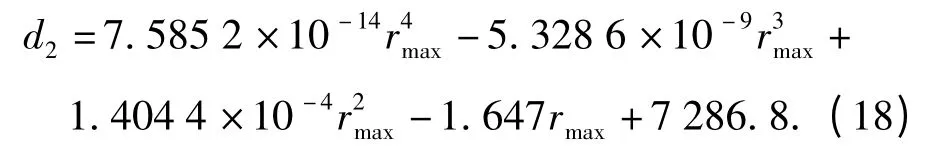
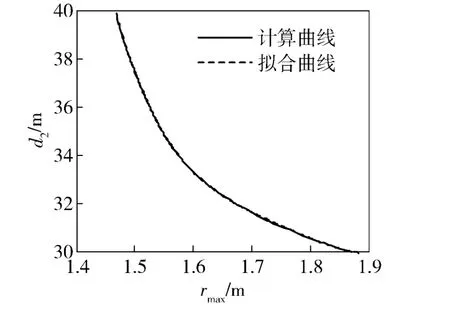
图4 d2与rmax的拟合曲线Fig.4 Fitting curve between d2 and rmax

利用(18)式求出(7)式中的p［g(rmax)］和g'(rmax)，继而利用(7)式求得rmax的概率分布p(rmax)，如图5所示。由图5可知概率密度最大时对应的距离为15.26 km，即为此时被动声纳的作用距离。

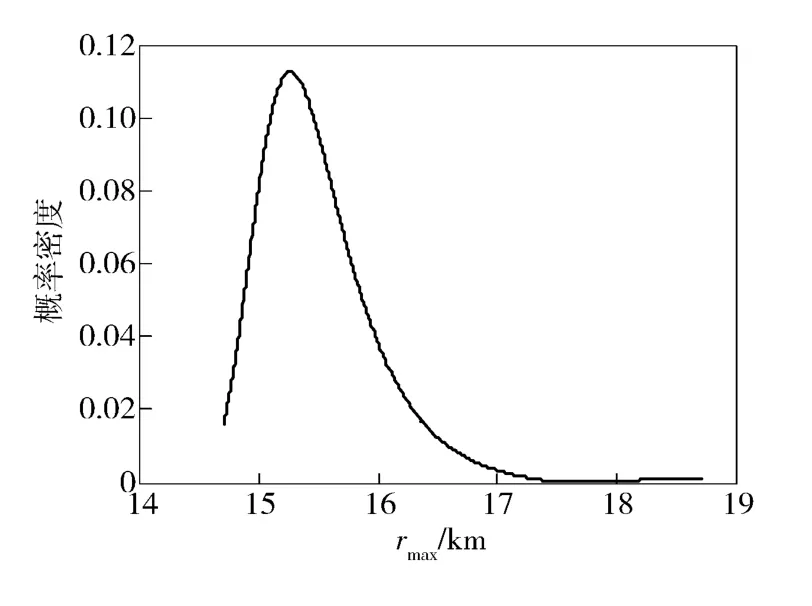
图5 单参数不确定时rmax的概率分布Fig.5 PDF of rmax with single uncertain parameter

2.2 多个海洋环境参数不确定

仿真条件:假定有2 个参数不确定，一个是温跃层下限深度d2，服从均值为35 m、标准差为2 m 的正态分布，另一个是海深H，在80 ～90 m 范围内服从均匀分布，其他条件与算例1 中的一致。

p(rmax)计算结果见图6，由图可知概率密度最大时对应的距离rMLE=15.05 km.

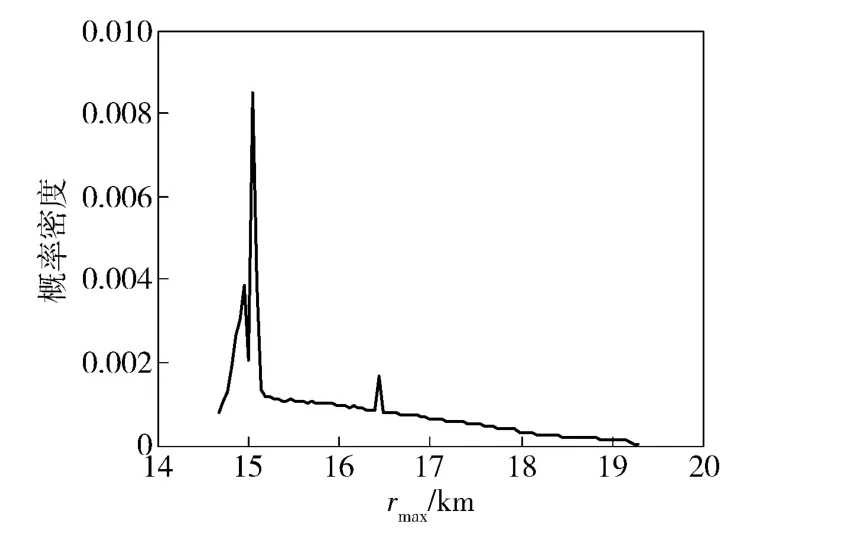
图6 两个参数不确定时rmax的概率分布Fig.6 PDF of rmax with two uncertain parameters

3 结论

针对目前预报不确定海洋环境中被动声纳作用距离方法的不足，基于极大似然准则提出了一种估计不确定海洋环境中被动声纳作用距离的计算方法，推导了当单个和多个海洋环境参数不确定时预报被动声纳作用距离的过程，并分别给出了算例。

本文方法克服了现有方法的不足，利用不确定环境参数ξ 的概率密度信息，获取rmax的概率分布，以极大似然准则确定被动声纳的作用距离rMLE. 本文方法对不确定海洋环境参数的概率分布不做特定要求，且无需设定用以确定作用距离的门限，该方法还可推广至不确定海洋环境中主动声纳作用距离的预报中，为不确定海洋环境下的水下作战提供声纳辅助决策信息。

References)

［1］Hodges R P. Underwater acoustics:analysis，design and performance of sonar［M］. Singapore:Markono Print Media Pte Ltd.，2010.

［2］程广利，张明敏. 浅海不确定声场的随机多项式展开法研究［J］. 声学学报，2013，38(3):294 -299.CHENG Guang-li，ZHANG Ming-min. On polynomial chaos expansion method for the uncertain acoustic field within shallow water［J］. Acta Acustica，2013，38(3):294 -299. (in Chinese)

［3］笪良龙. 海洋水声环境效应建模与应用［M］. 北京:科学出版社，2012.DA Liang-long. Modeling and application of underwater acoustic environmental effect［M］. Beijing:Scienc Press，2012. (in Chinese)

［4］Ferla C M，Porter M B. Receiver depth selection for passive sonar systems［J］. IEEE Journal of Oceanic Engineering，1991，16(3):267 -278.

［5］李凡，郭圣明，王鲁军，等. 一种新的声纳作用距离指标评估方法［J］. 声学技术，2009，28(3):235 -239.LI Fan，GUO Sheng-ming，WANG Lu-jun，et al. A new approach to prediction of sonar detection range index［J］. Technical Acoustics，2009，28(3):235 -239. (in Chinese)

［6］庄楚强，吴亚森. 应用数理统计基础［M］. 广州:华南理工大学出版社，2002.ZHUANG Chu-qiang，WU Ya-sen. Foundations of applied mathematical statistics［M］. Guangzhou:South China University of Technology Press，2002. (in Chinese)

［7］Jensen F B，Kuperman W A，Porter M B，et al. Computational ocean acoustics［M］. 2nd ed. New York:Springer，2011.