某导弹无依托发射场坪动态响应研究

周晓和,马大为,胡建国,仲建林

（南京理工大学机械工程学院,江苏南京 210094）

某导弹无依托发射场坪动态响应研究

周晓和,马大为,胡建国,仲建林

（南京理工大学机械工程学院,江苏南京 210094）

为得到某导弹无依托发射时场坪的动态响应,采用Hongnestad方程及改进后的Saenz单轴方程分别拟合混凝土在受压时的上升段及下降段应力-应变关系,构建了一条适用于沥青混凝土的受压应力-应变曲线；引入损伤因子并结合Sidiroff能量等价原理,建立了某导弹无依托发射场坪塑性损伤动态本构；基于含场坪的发射平台非线性结构动力学模型,分析了导弹在发射状态下场坪的动态响应。研究结果表明：在导弹垂直待发射阶段,后支腿处场坪比前支腿处场坪动态响应明显；在导弹垂直发射阶段,发射筒底部处场坪沉降较大,发射筒底部处场坪与后支腿处场坪交叉区域损伤严重。研究结果可为导弹无依托发射前场坪快速评估提供理论支撑。

兵器科学与技术；无依托发射；场坪；应力应变关系；塑性损伤；动态响应

0 引言

所谓无依托发射,就是导弹发射不再依托预准备的发射场地,而是随机选取场坪发射。该发射方式具有隐蔽性高、机动力强等特点,故无依托发射已经成为国内外陆基机动导弹的重要发展方向。我国公路修筑错综复杂,将公路作为发射场坪不仅满足了发射的随机性、隐蔽性,更提高了导弹的机动性。导弹公路发射要求在各等级的公路上均可实现安全发射,但我国公路仍存在性能较差的路面（如3级、4级公路）,在弹射载荷作用下路面将发生较大程度的下沉甚至损坏,将影响导弹发射精度及发射车整体的稳定性,故进行导弹发射时场坪与发射平台间的耦合效应研究显得尤为重要。姚晓光等[1-2]对导弹起竖阶段发射车整体响应及受力情况进行了论述,没有涉及导弹发射阶段的力学分析；张胜三[3]通过理论计算得到发射车各状态下支腿反力及稳定性计算公式,未对场坪受力情况进行研究；程洪杰等[4]将场坪划入发射平台内并通过理论计算得到导弹发射各阶段场坪受力计算公式,没有涉及具体的混凝土本构关系,无法对发射场坪动态响应进行详尽的研究。

我国3级、4级公路基本采用沥青混凝土材料进行铺设,该材料内部存在许多初始裂纹。塑性损伤本构模型可研究带微裂纹的材料在受力时损伤的扩展及演化,比较适合运用于导弹发射时沥青混凝土路面的动态响应研究。塑性损伤本构模型的建立需要混凝土材料受压、受拉应力-应变表达式,文献[5-6]中所运用的受压应力-应变表达式在混凝土轴心抗压强度较小情况下将会出现负应力的情况,并不适用于模拟沥青混凝土材料。

本文采用Hongnestad方程[7]及改进后的Saenz单轴方程[8-9],构建一条适用于沥青混凝土受压时的应力应变曲线,结合损伤理论及能量等效性假设,建立导弹无依托发射场坪面层的塑性损伤数值模型,进一步建立含发射场坪在内的发射平台非线性结构动力学模型。通过数值计算,得到在导弹发射不同阶段中前后支腿及发射筒底部处场坪的动态响应,重点研究场坪的沉降及损伤演化,并对发射平台与场坪之间的耦合作用效应进行一定的阐释。

1 沥青混凝土塑性损伤模型

1.1 塑性损伤本构模型

Lubliner等[10]、Lee等[11]提出的塑性损伤模型采用各向同性弹性损伤结合各向同性拉伸和压缩塑性理论来表征混凝土的非弹性行为,其屈服函数形式[11]为

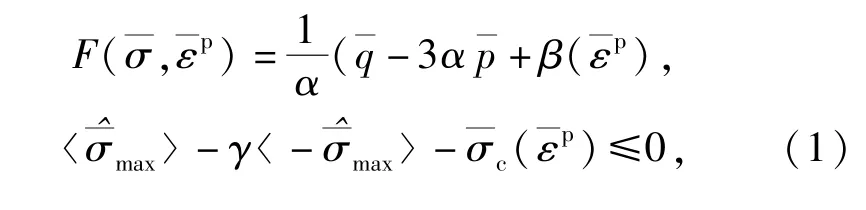
式中：λ为塑性因子；σt0为拉伸屈服应力；流动势G为Drucker-Prager双曲线函数；ψ为高围压下子午面内的剪胀角；∈为函数趋近于渐近线速率的参数。

塑性损伤模型损伤演化规律为

1.2 沥青混凝土应力-应变关系

沥青混凝土在受压时应力-应变曲线通常分为3个阶段[12]：σ≤0.3σ0时,σ0为极限应力,应力-应变曲线接近直线,应力-应变呈线性关系； 0.3σ0＜σ≤σ0,为沥青混凝土稳定裂纹扩展阶段； σ＞σ0,进入刚度退化段（下降段）。

首先采用Hongnestad方程来模拟沥青混凝土稳定裂纹扩展段,该方程将沥青混凝土稳定裂纹扩展段应力-应变关系近似为抛物线形,其表达式为

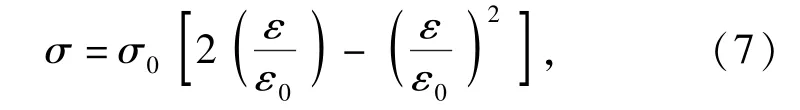
式中：σ0为沥青混凝土受压极限应力；ε0为极限应力所对应的应变。

其次,采用改进后的Saenz单轴方程来模拟沥青混凝土的下降段,其表达式为

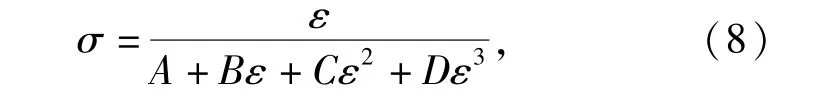
式中：A、B、C、D 4个参数可由5个控制方程确定。控制方程表达式为：ε=0时,σ=0,对应曲线原点； ε=0时,dσ/dε=E0,E0为线性段初始弹性模量,对应曲线原点；ε=ε0时,σ=σ0,对应曲线峰值点；ε=ε0时,dσ/dε=0,对应曲线峰值点；ε=εu时,σ= σu,对应曲线极限点。其中,εu为破坏极限点对应的应变,σu为破坏极限点对应的应力。沥青混凝土在开始受压时存在线性段,故控制方程第2条dσ/dε应等于E0,控制方程第1条自然满足,将余下3个条件代入（8）式中得

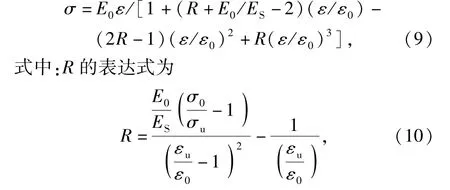
ES为曲线峰值点切线模量。由（7）式可知,E0/ES= 2.将（9）式与（10）式联立并带入σ0、ε0,得到R值大小。将R带入（9）式中便可得到沥青混凝土受压下降段应力-应变表达式。

最后将（7）式、（9）式及直线段表达式进行联立,并定义无量纲量x=ε/ε0,y=σ/σ0,得到沥青混凝土受压应力-应变曲线如图1所示,其表达式为

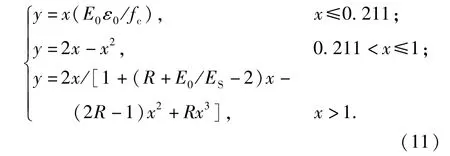
式中：fc为沥青混凝土轴心抗压强度。

沥青混凝土受拉时在到达极限应力前假设应力-应变曲线为直线,之后应力随应变的增大而非线性下降。沥青混凝土受压应力-应变曲线如图2所示,曲线表达式[13]为

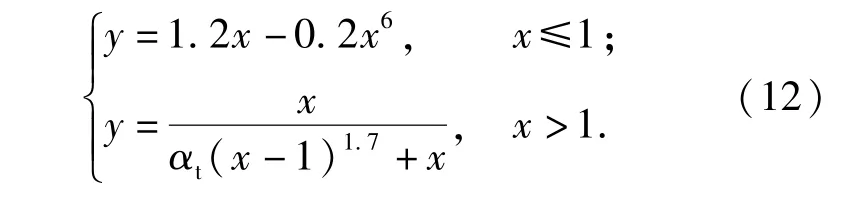
式中：αt=0.312,ft为沥青混凝土轴心抗拉强度。

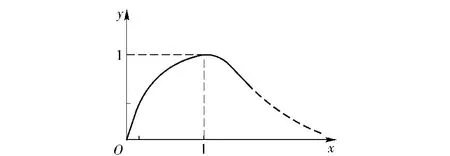
图1 混凝土受压应力-应变曲线Fig.1 Compressive stress-strain curve of concrete

图2 混凝土受拉应力-应变曲线Fig.2 Tension stress-strain curve of concrete

1.3 损伤因子d的推导

损伤演化方程的推导采用能量等效性假设,该方法可避免因使用应变等效假设而使得各向异性损伤模型中的有效弹性矩阵不对称的问题。根据Sidiroff的能量等价原理,应力作用在受损材料产生的弹性余能与作用在无损材料产生的弹性余能在形式上相同,只要将应力改为等效应力即可。

无损伤材料弹性余能

将（15）式带入到（11）式、（12）式中,即可推到出损伤因子d的计算公式。则沥青混凝土受压损伤因子计算公式为

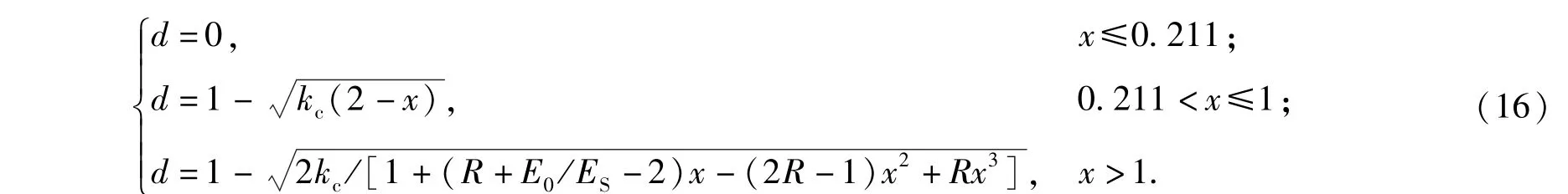
受拉损伤因子计算公式为

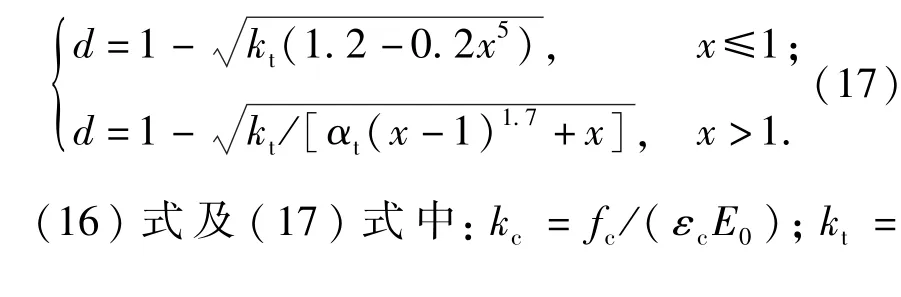
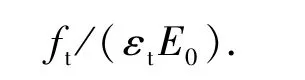
1.4 模型验证

采用有限元法数值模拟沥青混凝土非线性力学特性,并与三轴试验结果[14]进行对比,验证采用塑性损伤模型仿真方法的有效性。

仿真计算模型为直径100 mm,高为200 mm的圆柱体,模型尺寸与试样一致。沥青混凝土本构模型采用塑性损伤模型,压缩行为的屈服应力-压缩非弹性应变关系通过（11）式拟合并计算得到；拉伸行为的屈服应力-开裂应变关系通过（12）式拟合并计算得到；材料的受压、受拉非弹性应变与损伤因子的关系分别通过（16）式及（17）式计算得到。仿真过程分3步实现：首先对模型实现自重应力平衡,然后施加0.1 MPa围压,最后施加轴向载荷。仿真过程重点考查主应力差对轴向应变的影响,仿真与试验结果对比如图3所示。

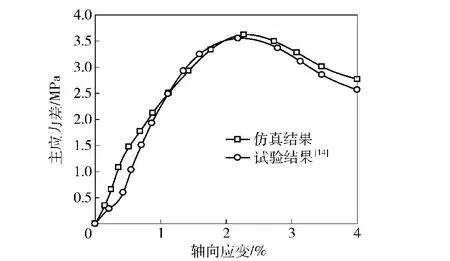
图3 主应力差-轴向应变仿真和试验结果对比Fig.3 Comparison of simulation and test results of deviator stress-axial strain

对比图3中仿真结果和试验结果可知,围压为0.1 MPa时,轴向应变在2%左右时开始屈服,屈服应力均在3.55 MPa左右。仿真和试验结果规律一致,结果数据吻合较好,验证了塑性损伤模型本构模型能较好地模拟沥青混凝土材料力学特性,仿真中材料受压时的应力-应变曲线的构建也较为合理。

2 含场坪的发射平台非线性结构动力学模型

含场坪的发射平台非线性结构动力学模型如图4所示。发射平台采用三铰点式起竖机构,在底盘对称位置设置4个液压千斤顶支腿将整车架起,轮组不再承受车体自重以及发射时作用力。发射筒底部采用自适应底座,在导弹垂直待发射阶段具有一定的离地高度。发射场坪从上至下依次为沥青混凝土面层、基层、底基层和土基,H1、H2、H3和H4分别表示各层介质厚度,M1为接触中心点处场坪,沿发射筒底部处场坪半径向前取M2、M3及M4.计算采用显式动态算法,并使用毫米-吨-秒-兆帕单位制。另外,在图中支腿及发射筒处场坪不同位置设置动态响应观测点（HL代表后左支腿处场坪、HR代表后右支腿处场坪、QL代表前左支腿处场坪、QR代表前右支腿处场坪、M代表发射筒处场坪）,便于更直观地观测场坪在导弹发射时的动态响应。定义的观察点代表该点附近一定范围内的介质。

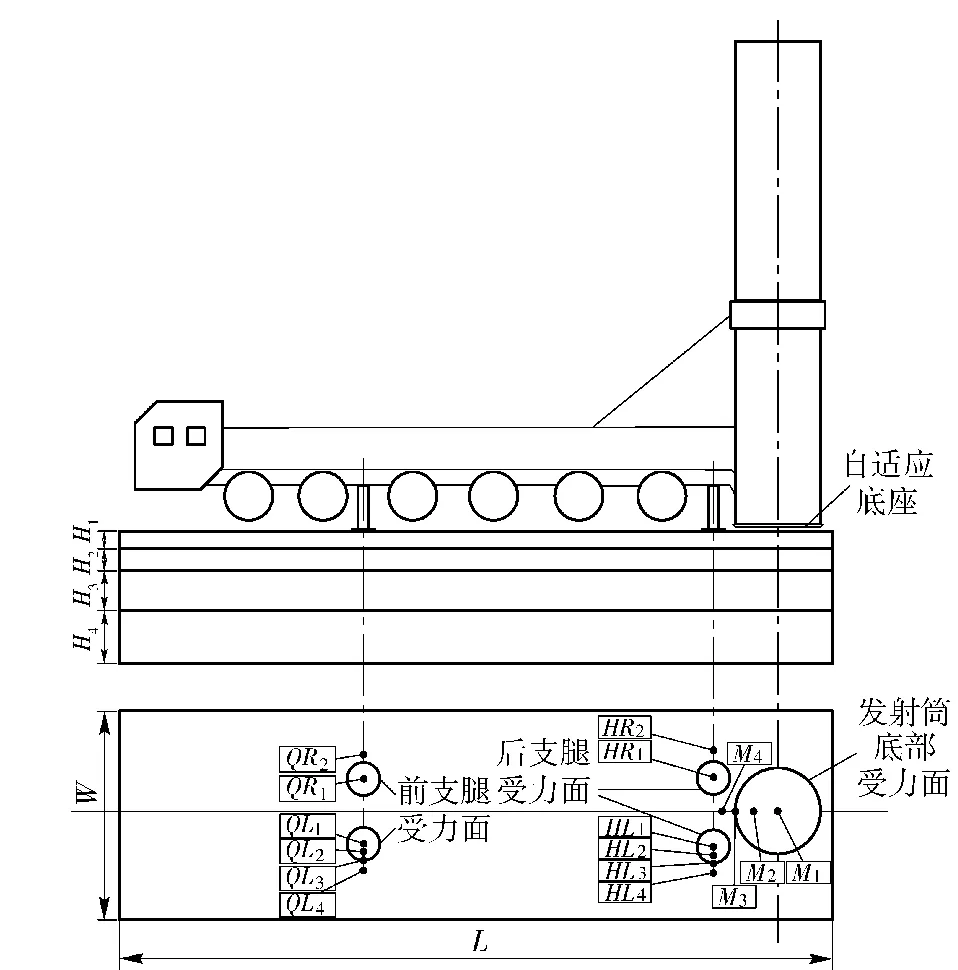
图4 含发射场坪的发射平台结构示意图Fig.4 Launching platform structure

沥青混凝土层采用塑性损伤模型对其进行有限元分析,其材料参数及结构参数如表1所示[12]。为了着重考虑沥青混凝土层在导弹发射时的动态响应,基层、底基层以及土基均设置成为线弹性材料,各层结构和材料参数见表2[15-16]所示。沥青混凝土层、基层、底基层及土基四周均设置为自由,土基底面设置为固端约束。

为重点研究无依托发射时场坪的动态响应,以某导弹无依托发射时对地载荷为输入条件,并根据载荷对称原理假定左右支腿处场坪受力相同,完成对含场坪的发射平台非线性结构动力学模型的合理简化。导弹发射时发射筒底部及液压支腿处场坪压力曲线如图5和图6所示,其中图5零时刻即为导弹待发射时支腿处场坪压力状态。

为提高计算精度,将无依托发射过程场坪动态响应过程分为两步：

第1步,为建立初始应力场平衡,只加载重力并采用静态分析技术,将计算后获得的给定边界条件和载荷相平衡应力状态作为初始条件带入动态分析中。将第1步分析计算过程称为导弹垂直待发射阶段。

表1 沥青混凝土层材料参数与结构参数Tab.1 The material parameters and structure parameters of asphalt concrete layer

表2 发射场坪材料参数与结构参数Tab.2 The material parameters and structure parameters of launching site

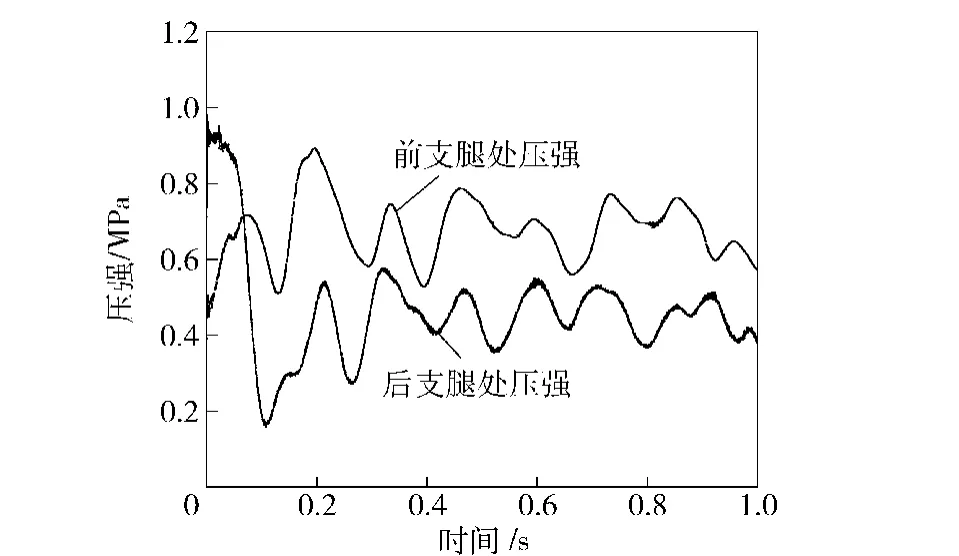
图5 导弹发射时支腿处场坪压力曲线Fig.5 Pressure curves of site during launching

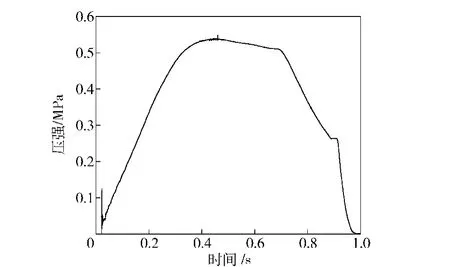
图6 发射筒底部处场坪压力曲线Fig.6 Pressure curve of site below the bottom of canister launcher

第2步导入第1步的计算结果作为路面的初始应力场,对模型施加动态载荷,以场坪各观测点处沉降和损伤情况评判沥青混凝土路面的工作状态。将第2步分析计算过程称为导弹发射阶段。

3 仿真结果与分析

3.1 液压支腿处场坪动态响应

表3为导弹发射阶段前、后支腿处各观测点场坪位移响应。由计算结果可以看出,导弹在发射零时刻支腿处场坪产生初始位移,这是因为在垂直待发射阶段由于发射平台自重导致支腿处场坪发生一定程度的沉降。后支腿处场坪初始位移大于前支腿处场坪,这将造成发射平台整体的前高后低。造成前后支腿初始位移差值的原因为：在导弹的起竖中发射平台重心后移,导致在垂直待发射阶段后支腿处场坪承受的压力大于前支腿处场坪。

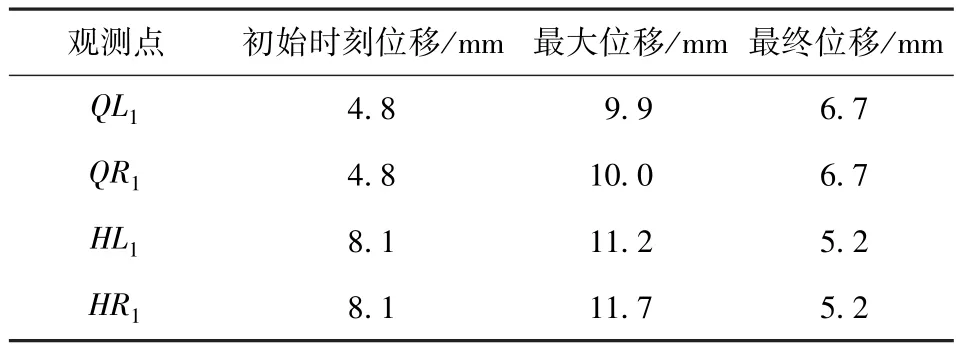
表3 发射阶段前、后支腿处场坪中心点垂向位移响应Tab.3 Vertical displacements of site middle points during launching

图7为导弹发射阶段后支腿处场坪中心点垂向位移曲线。该曲线在t=0.02 s时发生较大幅度的上升且在之后的位移响应过程中有较大幅度的振荡。产生这种现象原因为：垂直待发射阶段造成的发射平台整体的前高后低将导致导弹在发射过程中发射筒底部一定程度的倾斜,当倾斜的发射筒底部触地后与场坪发生复杂的接触,造成后支腿处场坪整体的沉降与隆起现象的出现。图7中左、右后支腿处场坪中心点垂向位移有一定差别,说明在发射载荷作用下,发射平台大梁产生了一定的扭转变形。

图8为导弹发射阶段前支腿处场坪中心点垂向位移曲线。该曲线的振荡是因为发射筒底部触地引起的发射车整体振动造成的。图8中左、右前支腿处场坪中心点垂向位移差别极小,但两曲线并不完全重合,说明发射平台大梁在前支腿处产生的扭转变形较小。

由于后支腿处场坪在导弹发射过程中受力复杂且变形较大,故取左后支腿处场坪沿半径方向不同点作为研究对象进行位移响应计算分析。表4与图9为导弹发射阶段左后支腿不同观测点处场坪垂向位移计算结果,由结果可知,离支腿作用面中心点越远,场坪位移响应越小,场坪位移曲线越平稳。

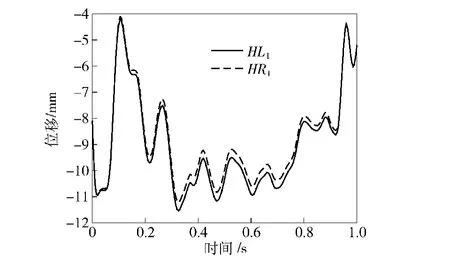
图7 发射阶段后支腿处场坪中心点垂向位移曲线Fig.7 Vertical displacement curves of site middle points below the posterior supports during launching

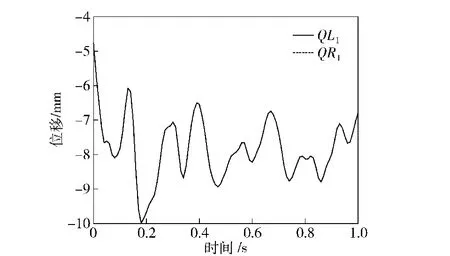
图8 发射阶段前支腿处场坪中心点垂向位移曲线Fig.8 Vertical displacement curve of site middle points below the front supports during launching

表4 发射阶段左后支腿不同观测点处场坪垂向位移响应Tab.4 Vertical displacement responses of site at different observation points below left posterior support during launching

导弹发射时支腿周围场坪介质发生损伤甚至断裂破坏将对发射平台整体稳定性造成影响,故取HL4及HR2、QL4及QL2四点处场坪进行损伤分析。表5与图10为导弹发射阶段前后支腿周边各观测点处场坪损伤计算结果。由结果可得：在导弹垂直待发射阶段,发射平台自重对支腿周边场坪造成一定程度的初始损伤；在导弹发射阶段,由于后支腿处场坪受力较大,使得该处场坪损伤始终比前支腿处周边场坪严重；由于发射筒底部与地面在发射过程中产生复杂的接触作用,导致后支腿处周边场坪受力环境复杂,将使得该处场坪中原本处于开裂或者扩展阶段的裂纹在不同方向的应力作用下发生闭合或重开裂,故后支腿处场坪损伤曲线振荡明显,损伤值处于不停变化中。

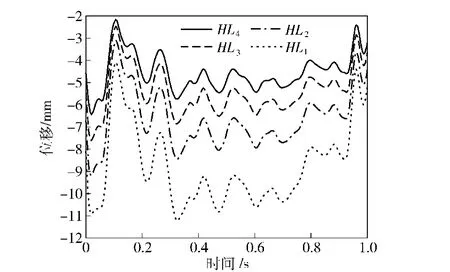
图9 发射阶段左后支腿不同观测点处场坪垂向位移曲线Fig.9 Vertical displacement curves of site at different observation points below the left posterior support during during

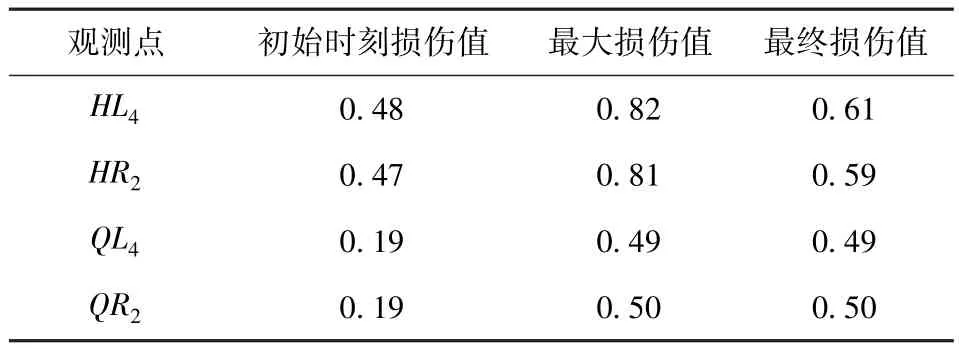
表5 发射阶段前后支腿周边各观测点处场坪场坪损伤响应Tab.5 Damage responses of site at different observation points around posterior support during emission stage

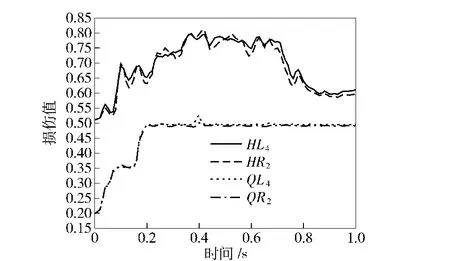
图10 发射阶段前后支腿周边各观测点处场坪损伤时间曲线Fig.10 Damage curves of site at different observation points around posterior support during launching

由于后支腿处场坪在导弹发射时损伤较严重,故取左后支腿处场坪沿半径方向不同点作为研究对象进行损伤响应分析。表6与图11为导弹发射阶段左后支腿不同观测点处场坪损伤计算结果。由结果可得,在导弹发射过程中,HL1与HL2点损伤较小且损伤曲线平稳,这是因为在发射平台自重及弹射载荷作用下HL1点及HL2点位于支腿底盘作用面内而始终处于被压缩状态。后支腿处场坪损伤最严重区域为后支腿底盘作用面边界（HL3）,这是因为在发射平台自重及弹射载荷作用下HL3点处场坪受到后支腿底盘对场坪的剪力作用而产生剪切损伤。

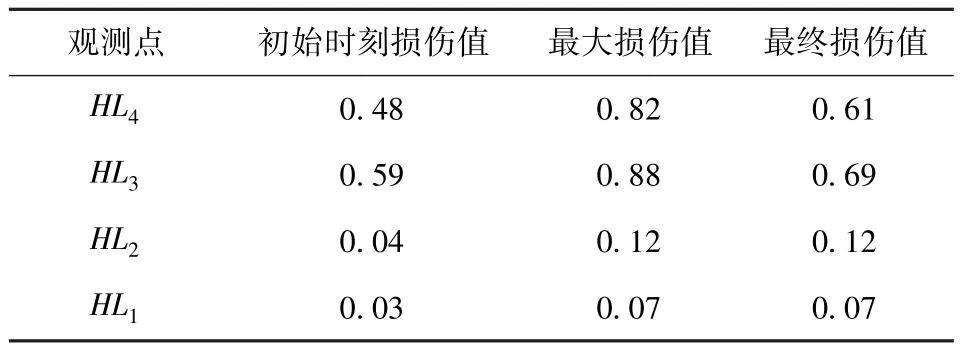
表6 发射阶段左后支腿不同观测点处场坪损伤响应Tab.6 Damage responses of site at different observation points below left posterior outrigger during launching

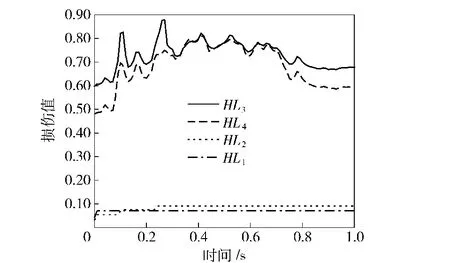
图11 发射阶段左后支腿不同观测点处场坪损伤时间曲线Fig.11 Damage curves of site at different observation points below left posterior outrigger during launching

3.2 发射筒底部处场坪动态响应

导弹弹射时发射筒底部在发射气体压力下触地并与场坪发生复杂的接触作用,导弹弹射出筒后发射筒内气压迅速减小,发射筒底部回缩离开场坪。整个过程对地面形成了强大的冲击力。

图12为导弹发射阶段发射筒底部处场坪加载中心点垂向位移曲线。曲线零时刻位移值为0,这是由于发射筒底部在发射初始时刻存在一定的离地高度,在导弹垂直待发射阶段并无作用力作用于发射筒底部处场坪。在导弹发射阶段,由于初始离地高度的存在使得曲线在t=0.027 s前接近于直线, t=0.027 s后发射筒底部触地并导致场坪发射沉降变形,其最大位移达到25.4 mm.

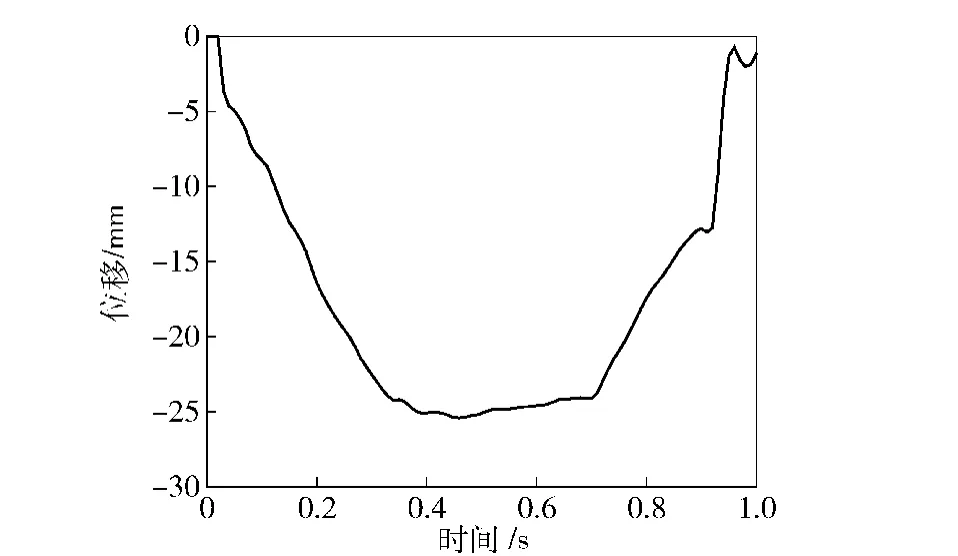
图12 发射阶段发射筒底部处场坪中心点垂向位移曲线Fig.12 Vertical displacement curve of site middle points below the bottom of canister launcher during launching

弹射过程中,发射筒底部触地与路面发生了复杂的接触作用。取路面与发射筒底部接触区域中4个不同位置进行分析,记接触中心点处场坪为M1,沿发射筒底部处场坪半径向前取M2、M3及M4,其中M3为发射筒底部作用面边界处场坪,M4为发射筒底部处场坪与后支腿处场坪交叉区域内点。

表7与图13为导弹发射阶段发射筒底部处场坪不同观测点垂向位移计算结果。由结果可得：在导弹垂直待发射阶段各观测点均未产生垂向位移,这是因为在这一阶段发射筒底部还未触地；在导弹垂直发射阶段,离发射筒底部处场坪中心点越远,各观测点最大沉降与最终沉降越小。

表7与图14为导弹发射阶段发射筒底部处场坪不同观测点损伤计算结果。由结果可得：发射筒底部处场坪不同观测点在零时刻产生不同程度的损伤,当观测点位置离后支腿处场坪越近初始损伤越大,这是由于在垂直待发射阶段后支腿处场坪动态响应对发射筒底部处场坪动态响应产生一定程度的影响,且当离后支腿处场坪越近,影响越大。在导弹发射过程中,M1及M2处场坪损伤平稳且损伤值较小,这是因为在弹射载荷作用下M1及M2处场坪处于被压缩状态。M3点处场坪位于发射筒底部作用面边界处,在弹射载荷的作用下该点处场坪受拉伸应力作用而产生拉伸损伤,故该点处场坪损伤值较大。M4点处场坪位于发射筒底部处场坪与支腿处场坪交叉区域,该区域内场坪承受来自发射筒底部处场坪及后支腿处场坪不同方向的拉、压应力波作用,力学环境较为复杂,故该区域损伤最严重。

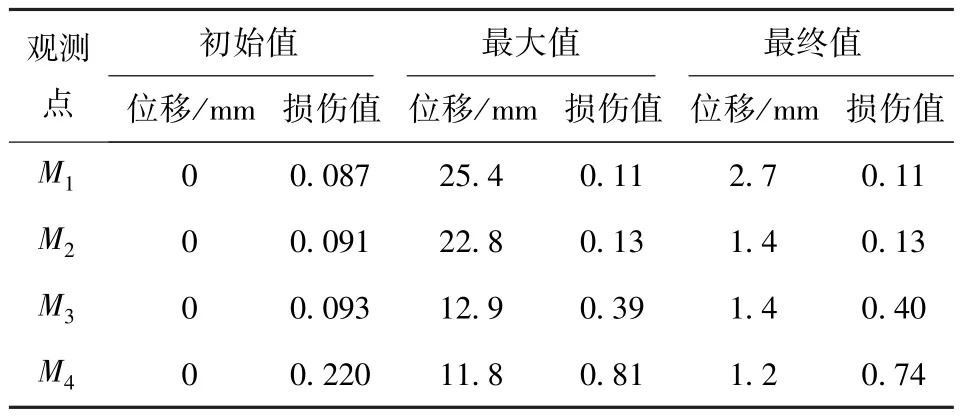
表7 发射阶段发射筒底部处场坪不同观测点动态响应Tab.7 Dynamic responses of different observation points below the bottom of canister launcher during launching

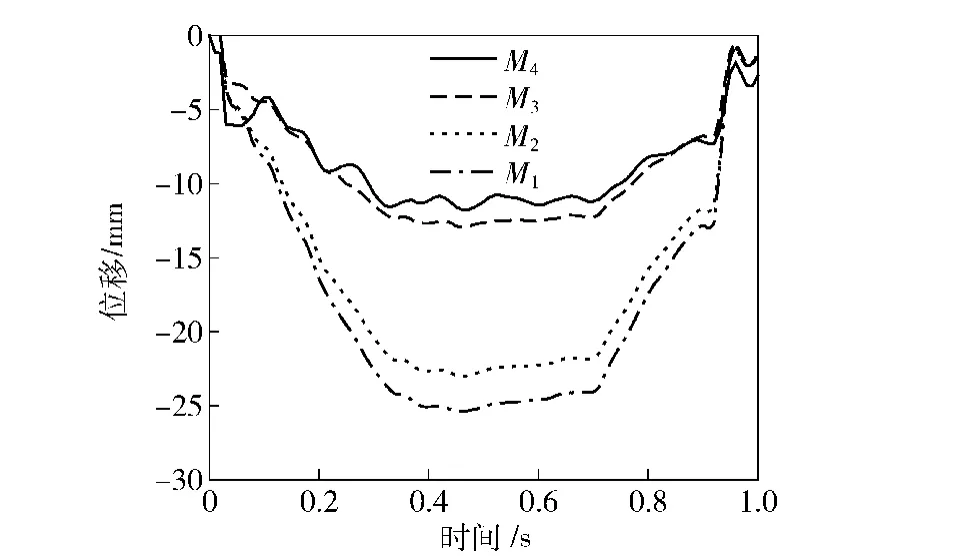
图13 发射阶段发射筒底部处场坪不同观测点垂向位移曲线Fig.13 Vertical displacement curves of site different observation points below the bottom of canister launcher during launching

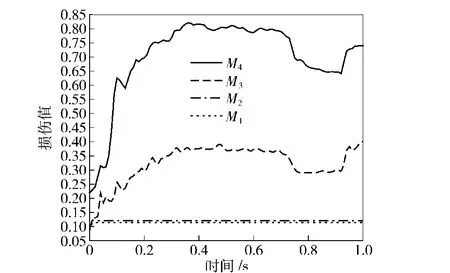
图14 发射阶段发射筒底部处场坪不同观测点损伤时间曲线Fig.14 Damage curves of site at different observation points below the bottom of canister launcher during launching

由图14可知,在t=0.9 s左右时,M3及M4处场坪损伤时间曲线出现突变上升现象。这是因为随着导弹的离筒,发射筒底部因压力的急剧减小而回收,发射筒底部处场坪在基层与底基层的作用下发生回弹,致使M3及M4处场坪受到来自底层的回弹应力作用,导致M3及M4处场坪损伤值加大。

4 结论

通过对某导弹无依托发射场坪动态响应的数值分析,获得以下4点结论：

1）根据构建的沥青混凝土受压应力-应变曲线,采用塑性损伤本构模型建立了沥青混凝土有限元模型,并与试验结果对比,验证了文中所采用的塑性损伤本构模型可以有效地模拟沥青混凝土非线性力学特性。

2）导弹在垂直待发射阶段发射平台整体表现为前高后低,后支腿处场坪比前支腿处场坪沉降值大,损伤比前支腿处场坪严重。

3）导弹在发射阶段场坪沉降最大响应为：发射筒底部处场坪＞后支腿处场坪＞前支腿处场坪；离发射筒底部处场坪及后支腿处场坪中心点越远,沉降越小。

4）导弹在发射阶段场坪损伤最终响应为：后支腿处场坪与发射筒底部处场坪交叉区域＞后支腿处场坪＞前支腿处场坪＞发射筒底部作用面处场坪；后支腿处场坪损伤最终响应为：后支腿底盘作用面边界处场坪＞后支腿作用面周边场坪＞后支腿作用面内场坪；发射筒底部作用面处场坪损伤最终响应为：发射筒底部作用面边界场坪＞发射筒底部作用面内场坪。

（References）

[1] 姚晓光,郭晓松,冯永保,等.导弹起竖过程的载荷研究[J].兵工学报,2008,29（6）：718-722.

YAO Xiao-guang,GUO Xiao-song,FENG Yong-bao,et al.Load analysis on missile erection[J].Acta Armamentarii,2008, 29（6）：718-722.（in Chinese）

[2] 姚晓光,郭晓松,冯永保,等.导弹起竖系统的仿真研究[J].兵工学报,2007,28（1）：23-27.

YAO Xiao-guang,GUO Xiao-song,FENG Yong-bao,et al.Simulation and research on missile erecting system[J].Acta Armamentarii,2007,28（1）：23-27.（in Chinese）

[3] 张胜三.由试验推算燃气流冲击力[J].导弹与航天运载技术,2001（4）：27-31.

ZHANG Sheng-san.Calculation impulsive force of combustion-gas flow by measure-ment in test[J].Missiles and Space Vehicles, 2001（4）：27-31.（in Chinese）

[4] 程洪杰,钱志博,赵媛,等.导弹起竖过程中的对地荷载研究[J].兵工自动化,2011,30（11）：1-3,19.

CHENG Hong-jie,QIAN Zhi-bo,ZHAO Yuan,et al.Study on the load to ground on missile erection process[J].Ordnance IndustryAutomation,2011,30（11）：1-3,19.（in Chinese）

[5] 李宇杰,何平,秦东平.基于混凝土弹塑性损伤本构模型的盾构管片受力分析[J].中国铁道科学.2012,33（1）：47-53.

LI Yu-jie,HE Ping,QIN Dong-ping.Force analysis of segment for shield tunnel based on elastoplastic damage constitutive model of concrete[J].China Railway Science,2012,33（1）：47-53. （in Chinese）

[6] 曹明.ABAQUS损伤塑性模型损伤因子计算方法研究[J].交通标准化,2012（2）：51-54.

CAO Ming.Research on damage plastic calculation method of ABAQUS concrete damaged plasticity model[J].Transportation Standardization,2012（2）：51-54.（in Chinese）

[7] 赵洁,聂建国.钢板-混凝土组合梁的非线性有限元分析[J].工程力学,2009,26（4）：105-112.

ZHAO Jie,NIE Jian-guo.Nonlinear finite element analysis of steel plate-concrete composite beams[J].Engineering Mechanics, 2009,26（4）：105-112.（in Chinese）

[8] 常晓林,马刚,刘杏红.基于复合屈服准则的混凝土塑性损伤模型[J].四川大学学报：工程科学版,2011,43（1）：1-7.

CHANG Xiao-lin,MA Gang,LIU Xing-hong.Damaged plasticity model for concrete structure based on composite yield criterion[J]. Journal of Sichuan University：Engineering Science Edition, 2011,43（1）：1-7.（in Chinese）

[9] 许斌,陈俊名,许宁.钢筋混凝土剪力墙应变率效应试验与基于动力塑性损伤模型的模拟[J].工程力学,2012,29（1）： 39-45,63.

XU Bin,CHEN Jun-ming,XU Ning.Test on strain rate effects and its simulation with dynamic damaged plasticity model for RC shear walls[J].Engineering Mechanics,2012,29（1）：39-45, 63.（in Chinese）

[10] Lubliner J,Oliver J,Oller S,et al.A plastic-damage model for concrete[J].International Journal of Solids and Structures, 1989,25（3）：229-326

[11] Lee J,Fenves G L.Plastic-damage model for cyclic loading of concrete structures[J].Journal of Engineering Mechanics,1998, 124（8）：892-900.

[12] 江见鲸,陆新征,叶列平.混凝土结构有限元分析[M].北京：清华大学出版社,2004.

JIANG Jian-jing,LU Xin-zheng,YE Lie-ping.Finite element analysis of concrete structures[M].Beijing：Tsinghua University Press,2004.（in Chinese）

[13] 中华人民共和国建设部.GB50010—2002混凝土结构设计规范[S].北京：中国建筑工业出版社,2002.

Ministry of Construction of the People's Republc of China. GB50010—2002 Concrete structure design specification[S]. Beijing：China Architecture and Building Press,2002.（in Chinese）

[14] 王为标,吴利言.沥青含量影响沥青混凝土应力应变关系的探讨[J].西安理工大学学报,1995,11（2）：129-133,140.

WANG Wei-biao,WU Li-yan.The effects of asphalt contents on stress-strain relations of asphalt concrete[J].Journal of Xi'an University of Technology,1995,11（2）：129-133,140.（in Chinese）

[15] 王金昌,朱向荣.软土地基上沥青混凝土路面动力分析[J].公路,2004（3）：6-11.

WANG Jin-chang,ZHU Xiang-rong.Dynamic analysis of asphalt concrete pavement on soft clay ground[J].Highway,2004（3）： 6-11.（in Chinese）

[16] 柳志军,刘春荣,胡朋,等.土基回弹模量合理取值试验研究[J].重庆交通学院学报,2006,25（3）：62-64.

LIU Zhi-jun,LIU Chun-rong,HU Peng,et al.Experiment study on reasonable evaluation of rebound modulis of subgrade[J]. Journal of Chongqing Jiaotong College,2006,25（3）：62-64. （in Chinese）

Research on Dynamic Response of Launching Site for Missile Unsupported Random Launch

ZHOU Xiao-he,MA Da-wei,HU Jian-guo,ZHONG Jian-lin
（School of Mechanical Engineering,Nanjing University of Science and Technology,Nanjing 210094,Jiangsu,China）

To obtain the dynamic response of launching site,the Hongnestad equation and improved Saenz equation are used to construct the upward and downward stress-strain curves of compressed concrete,which is suitable for asphalt concrete.Damage factor and Sidiroff energy equivalent principle are introduced to establish a plastic damage dynamic constitutive model of launching site for missile unsupported random launch.The dynamic response of the site during launching is analyzed based on nonlinear structural dynamics model considering launching site.The results show that the dynamic response of site below back supports is more significant than that below front support before missile launching.The settlement of site below the bottom of canister launcher is larger,and the sites below the back supports and the bottom of canister launcher are seriously damaged during launching.

ordnance science and technology；unsupported random launching；launching site；stressstrain relationship；plastic-damage；dynamic response

TJ03

A

1000-1093（2014）10-1595-09

10.3969/j.issn.1000-1093.2014.10.012

2013-10-02

国家自然科学基金项目（51303081）；江苏省自然科学基金项目（BK20130761）

周晓和（1988—）,男,博士研究生。E-mail：xiaohezhou@126.com；马大为（1953—）,男,教授,博士生导师。E-mail：ma_dawei@njust.edu.cn