基于数据融合和改进新陈代谢不等间距GM（1,1）模型的导弹装备故障预测

赵建忠,叶文,张磊

（1.海军航空工程学院兵器科学与技术系,山东烟台 264001；2.海军航空工程学院科研部,山东烟台 264001）

基于数据融合和改进新陈代谢不等间距GM（1,1）模型的导弹装备故障预测

赵建忠1,叶文1,张磊2

（1.海军航空工程学院兵器科学与技术系,山东烟台 264001；2.海军航空工程学院科研部,山东烟台 264001）

针对导弹装备故障预测中存在数据采样时间间隔不均匀、采样难度大、数据量小等问题,借鉴数据融合技术和灰色预测理论,提出一种基于数据融合和改进新陈代谢不等间距灰色模型（AMUGM（1,1））的预测方法。建立改进初始值选取和背景值构造的不等间距灰色模型,并通过残差修正和新陈代谢相结合的方式对模型进行优化；基于加权思想提出了隶属度加权法,以确定各模型的隶属度权值；根据隶属度权值和AMUGM（1,1）模型建立特定个体的故障预测模型。实例仿真验证了该方法的有效性。

兵器科学与技术；故障预测；灰色模型；不等间距GM（1,1）模型；数据融合

0 引言

故障预测对制定导弹装备维修计划,降低导弹装备保障费用,提高导弹装备战备完好率及避免因装备故障造成安全事故等方面具有重大意义。本文中导弹装备主要是指导弹地面保障设备,以导弹测试设备、计量设备、监控设备等电子设备为主,其系统组成复杂,结构关系模糊,特征参数获取往往是不完整和不确定的,这成为故障预测实现的难点。灰色系统理论为“贫信息”、“少数据”、“不确定性”导弹装备故障预测提供了一种新的途径[1],是当前故障预测的一种有效方式。首先,GM（1,1）模型通常选取第一个数据作为初始值,根据模型原理可知,这样会降低模型的精度[2]；其次,常见的GM（1,1）模型及其改进型大都基于等时距建立的,而导弹装备故障预测实践中,由于种种原因可能致数据缺失,呈现非等间隔期的状态数据,这就大大限制了GM（1,1）模型的适用范围,且等时距是不等时距的一个特例[3]。因此,建立不等时距的灰色预测模型具有重要的现实意义。但传统不等间距GM（1,1）模型（UGM（1,1））[4-5]背景值的构造采取中分值的形式,当灰色模型发展系数较大时影响模型的预测精度[6]；在预测过程中,随着预测周期的增加,最近更新的数据对于研究对象状态的反映往往更为准确[7]；当UGM（1,1）模型的预测结果不能满足精度要求时,往往需要进行残差修正。此外,还有如何充分利用导弹装备故障信息的问题,特别是同类产品性能退化轨迹存在很大关联性的情况下更是如此。

为了解决“数据量小,数据采样时间间隔不均匀”时导弹装备的故障预测问题,本文提出一种基于数据融合和改进的新陈代谢不等间距灰色预测模型（AMUGM（1,1））相结合的导弹装备故障预测方法。

1 问题描述

如果某型导弹装备在恒定应力水平下工作,其某项性能参数（电流、电压或者功率等）y会随着运行时间t呈单调递增或递减的趋势变化,当y达到失效阈值η时装备发生故障。已知d个同类型装备的性能退化数据,记第i个装备的第j次测量时刻为tij（i=1,2,…,p；j=1,2,…,n）,对应的性能退化测量值为yij,共测量ni次。第i个装备的性能退化数据为

基于同类型导弹装备的性能退化数据Di（i= 1,2,…,p）和特定装备Z的历史测量数据DZ建立Z的性能退化轨迹模型,即y与t之间的函数关系为

结合η预测Z的故障时间T,即求解η=fZ（T）从而得到故障发生时刻预测值T.根据Z的监测数据（t, yZj）,对（1）式进行更新并实现故障预测。

2 AMUGM（1,1）模型的建立

通过改进UGM（1,1）模型初始值选取方式、背景值构造形式以及残差修正,并运用新陈代谢思想对样本数据进行及时更新,建立AMUGM（1,1）模型。

2.1 初始值的改进

运用灰色自适应模型思想,对UGM（1,1）模型中的初始值选取方式进行改进。设能实现最佳预测效果的模型初始值为（t1）+ci,ci为一个未知优化量。则白化微分方程的时间响应函数变为

式中：a和b为系数。

对于优化量ci,其生成序列预测值的误差为

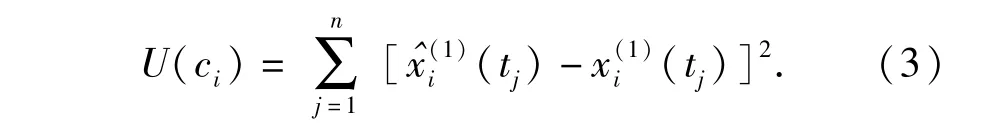
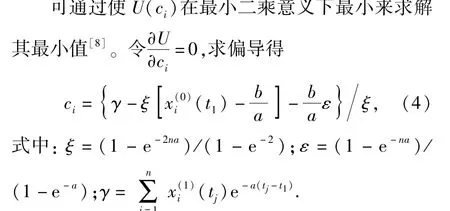
2.2 背景值的改进

由UGM（1,1）的建模过程可知,白化微分方程[9]为

2.3 残差修正

运用傅里叶变换对UGM（1,1）模型的残差序列进行修正,可补偿灰色预测的随机误差,提高预测精度[11]。

2.4 新陈代谢

3 基于数据融合和AMUGM（1,1）模型的故障预测

导弹装备故障信息是典型的多源信息,同一研究对象处于不同的环境、不同的安装部位、不同的信息采集手段时,所形成的性能退化轨迹就可能不同。因此,必须运用一种有效的方法合理协调导弹性能退化数据,充分综合有用信息,提高在多变环境中准确预测故障的能力。数据融合技术常被用于多源数据的处理,能够有效地消除数据中信息的不确定因素,使系统综合结果比其各组成部分更具有可信性。针对同类产品性能退化数据之间的关联性,本文在借鉴组合预测思想的基础上,提出一种基于隶属度的导弹性能退化数据融合的故障预测方法。通过各个故障预测模型的计算结果和实际数据的误差来动态地改变各个模型的权重,更好地充分利用同类产品的性能退化数据,使特定个体的故障预测更加准确可靠。

本文所提出的故障预测方法可分为2个阶段：1）建模阶段。对同类型装备和特定装备进行AMUGM（1, 1）建模；2）预测阶段。首先确定特定装备对各个模型的隶属度,然后基于隶属度权值和AMUGM（1,1）模型建立特定装备的性能退化轨迹模型,实现故障预测。具体如图1所示。

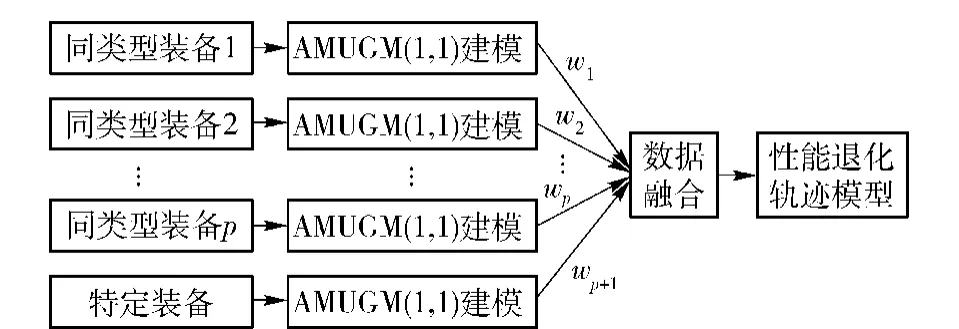
图1 基于数据融合和AMUGM（1,1）的故障预测框架图Fig.1 The frame diagram of failure prediction based on data fusion and AMUGM（1,1）

3.1 单个性能退化轨迹模型建立

首先根据AMUGM（1,1）建模原理,运用同类型装备的监测数据Di={（tij,yij）|i=1,2,…,p；j=1, 2,…,ni},建立p个基于AMUGM（1,1）的故障预测模型；再运用特定装备Z的历史监测值yZj,建立第p+1个基于AMUGM（1,1）的故障预测模型,一起记为{fi（t）|i=1,2,…,p+1}.

3.2 隶属度权值的确定

确定隶属度权值的方法多种多样,但目前还未有一个公认的统一原则。在对实际情况进行处理时,通常根据研究对象特点依据经验来合理地确定隶属度权值。聚类分析中Euclid距离是经常使用的概念[13-14]。导弹装备性能退化数据融合,可以看作一个多属性分类问题,能够借助Euclid距离来实现。本文基于Euclid距离概念,通过利用各故障预测模型对特定个体故障预测准确率的贡献来确定各故障预测模型的隶属度权值。

3.3 故障预测实现

首先将特定装备Z的历史测量时刻tZ分别代入p+1个AMUGM（1,1）模型,求取p+1个预测值yi；然后计算特定装备Z的测量值yZ与yi的Euclid距离dZi；再根据dZi确定出Z对各AMUGM（1,1）模型的隶属度权值wi（i=1,2,…,p+1）,对p+1个AMUGM（1,1）模型进行加权得到特定装备Z的性能退化轨迹模型fZ（t）；最后结合Z的实时测量数据[t,yZj]对tZ和yZ进行扩充,依次更新yi、dZi和wi,实现fZ（t）的及时更新,并结合η进行故障预测,称之为隶属度加权法（DWM）。

DWM的实现步骤如下：

4 实例分析

电源组合是导弹制导雷达系统的重要组成部分,用于提供雷达装备工作所需的各种稳压电源。电源组合的失效方式为退化失效,通常测试的是电压信号,即发现输出电压有一定的偏离但还不足以需要维修时,就需要密切关注其输出电压并能对其进行准确的故障预测。下面以某型导弹制导雷达系统的波束控制系统中一路电源为例,其结构原理如图2所示,输出为±15 V稳定直流电。具体工作过程：400 Hz的220 V交流电经电桥整流后,送到变压器中进行降压；然后通过全波整流和滤波变成直流；最后通过串联负反馈稳压电路输出15 V直流电压,最大不超过20 V,否则电源组合会发生故障。该电源对波束控制系统的影响主要由电源电压的退化引起,因此电源电压的监测是一项重要工作,表1给出了3组该型电源的电压监测采样值。

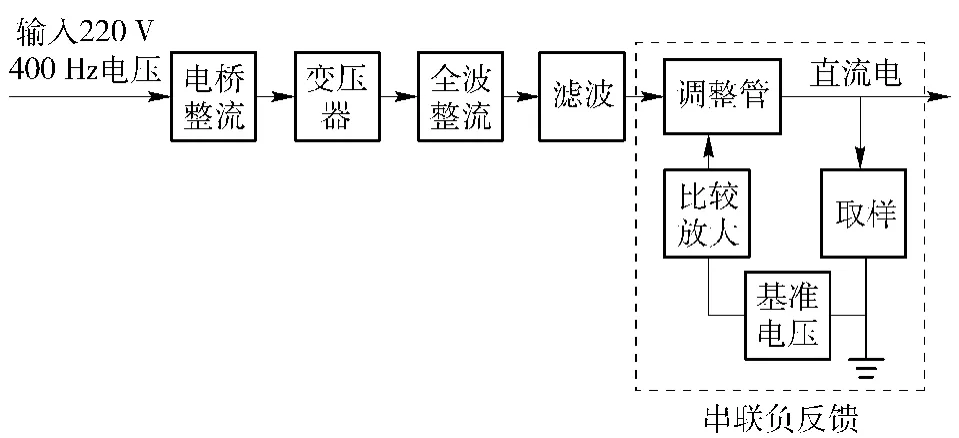
图2 某型电源原理框图Fig.2 Functional block diagram of a power supply

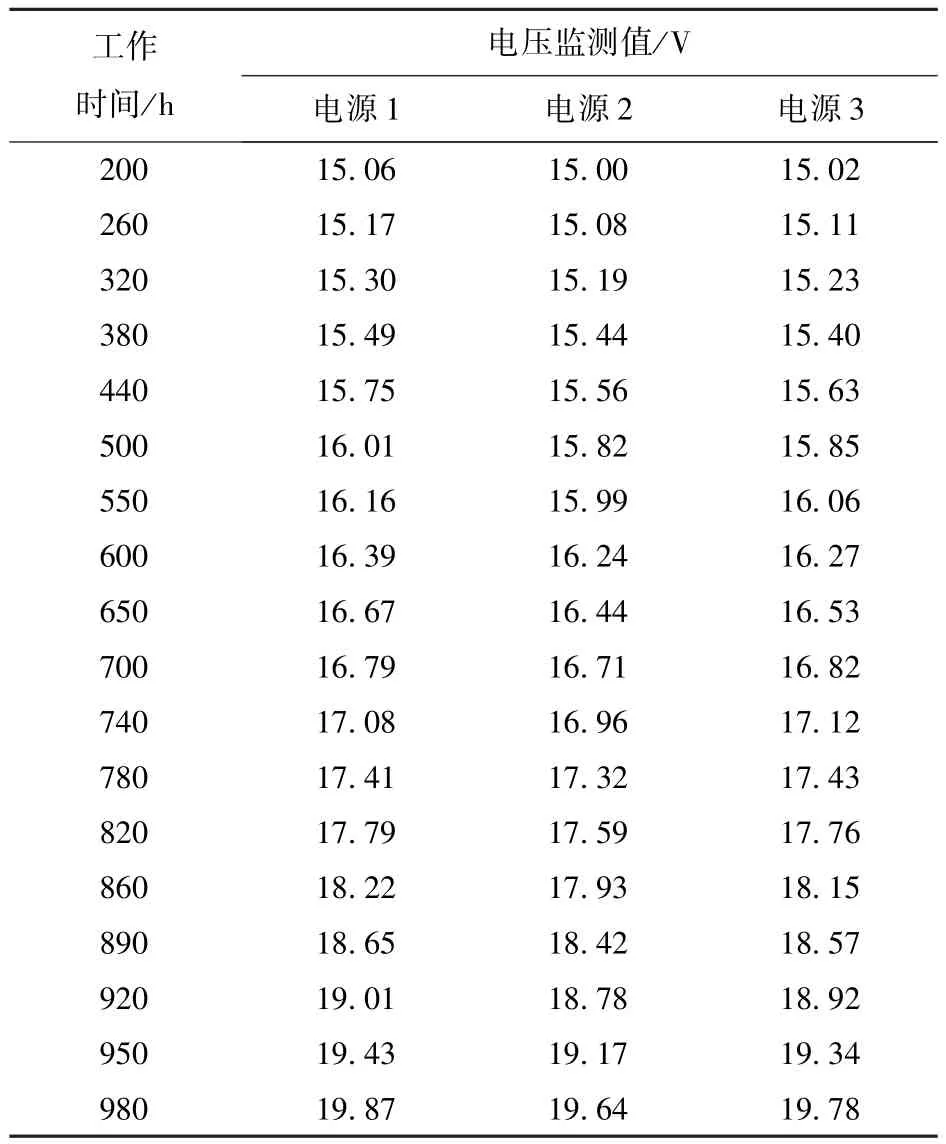
表1 某型电源的状态监测数据Tab.1 State monitoring data of a power supply

4.1 模型建立

对于同类型装备1和2,从第2个数据开始的前13组数据用于构建预测模型；对于特定装备3,从第1个数据开始的前13组数据用于构建预测模型,后5组数据作为预测检验数据。采用基于数据融合和AMUGM（1,1）模型相结合的方法进行故障预测,使用Matlab软件进行仿真计算分析。

依次类推,直到得到全部数据。

4.2 故障预测

同时,将数据融合和AMUGM（1,1）模型相结合的预测方法与传统UGM（1,1）模型和AMUGM（1, 1）模型的预测结果进行比较分析,以便证实本文预测方法的有效性,各预测方法或模型的拟合效果及预测结果分别如表2、图3以及表3、图4所示。其中,预测效果通过预测值、相对误差和平均相对误差来衡量。

4.3 结果分析

从表2、图3以及表3、图4中可以看出,精度最差的是传统UGM（1,1）模型,其次是AMUGM（1,1）模型,本文的预测方法拟合效果最好、预测精度最高。一方面AMUGM（1,1）模型采用改进初始值选取方法、改进背景值构造形式及新陈代谢思想,对建模过程进行了改进和优化,使得预测精度有了大幅度提高；另一方面在AMUGM（1,1）模型的基础上,还通过数据融合技术充分利用了同类型装备的故障信息,使预测结果的相对误差减小了一半,说明该方法的预测效果是明显的。

表2 不同方法的拟合值及相对误差Tab.2 Simulated values and relative percent age errors of different methods

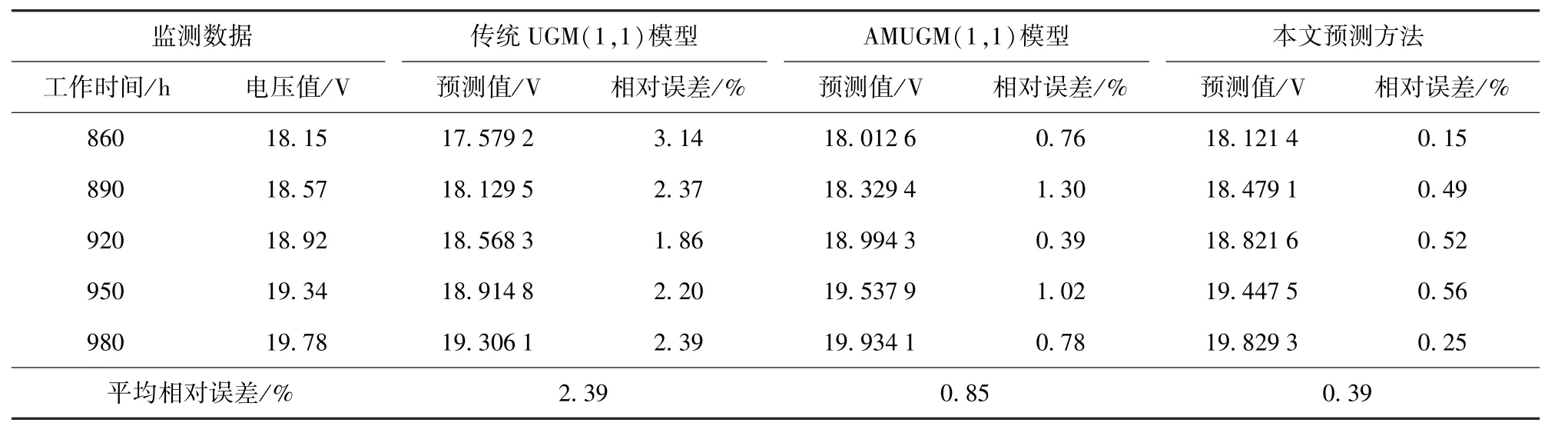
表3 不同方法的预测值及相对误差Tab.3 Predicted values and relative percent age errors of different method

图3 不同方法的拟合结果图Fig.3 Simulation results of different methods

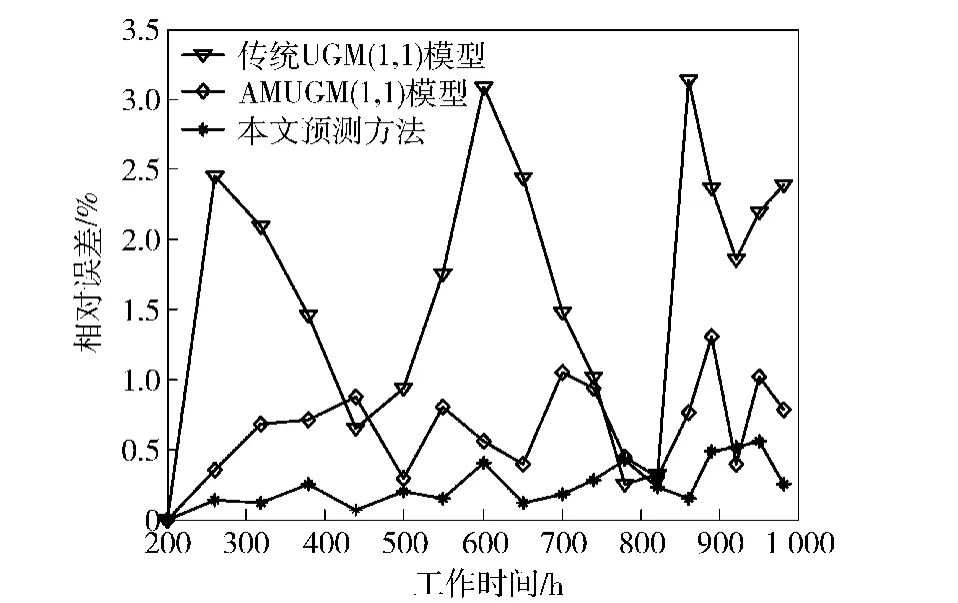
图4 不同方法的预测结果图Fig.4 Prediction results of different methods

5 结论

故障预测的准确性直接关系到导弹装备能否得到快速、高效的保障。本文在对不等间距灰色预测模型研究的基础上,借鉴组合预测思想,提出了基于数据融合技术和AMUGM（1,1）模型的导弹装备故障预测方法,其显著特点是运用指数曲线改进了UGM（1,1）背景值的构造方式,提高了模型的预测精度。此外,还通过隶属度加权法充分利用了同类型装备的性能退化数据,为导弹装备故障预测提供了一种新的思路和方法。

（References）

[1] 刘思峰,党耀国,方志耕.灰色系统理论及其应用[M].北京：科学出版社,2004：2-4.

LIU Si-feng,DANG Yao-guo,FANG Zhi-geng.Grey system theory and it's application[M].Beijing：Science Press,2004：2-4. （in Chinese）

[2] Chen Z J,Li L,Xiao X P.GM（1,1）odel and it's application to controlling the inverted camber of widening concrete bridge[J]. Journal of Grey System,2006,32（4）：365-374.

[3] Tseng F M,Yu H C,Tseng G H.Applied hybrid grey model to forecast seasonal time series[J].Technological Forecasting and Social Change,2001,67（2/3）：291-302.

[4] Kumar U,Jain V K.Times series models（Grey-Markov,Grey model with rolling mechanism and singular spectrum analysis）to forecast energy consumption in India[J].Energy,2010,35（4）： 1709-1716.

[5] Kuo H,Wu L J.Prediction of heat-affected zone using grey theory[J].Journal of Materials Processing Technology,2002,120： 151-168.

[6] Trivedi H V,Singh J K.Application of grey system theory in the development of a runoff prediction model[J].Biosystems Engineering,2005,92（4）：521-526.

[7] Chen S,Li Z G,Xu Q S.Grey target theory based equipment condition monitoring and wear mode recognition[J].Wear,2006, 260（4/5）：438-449.

[8] 罗为,刘鲁.基于偏最小二乘法的军用无人机研制费用预测[J].北京航空航天大学学报,2010,36（6）：667-670.

LUO Wei,LIU Lu.Prediction of military UAV development cost based on partial least-square regression method[J].Journal of Beijing University of Aeronautics and Astronautics,2010,36（6）： 667-670.（in Chinese）

[9] 王正新.振荡型GM（1,1）幂模型及其应用[J].控制与决策, 2013,28（10）：1459-1464.

WANG Zheng-xin.Oscillating GM（1,1）power model and its application[J].Control and Decision,2013,28（10）：1459-1464.（in Chinese）

[10] 王叶梅,党耀国,王正新.非等间距GM（1,1）模型背景值的优化[J].中国管理科学,2008,16（4）：159-163.

WANG Ye-mei,DANG Yao-guo,WANG Zheng-xin.The optimization of background value in non-equidistant GM（1,1） model[J].Chinese Journal of Management Science,2008,16（4）： 159-163.（in Chinese）

[11] Kayacan E,Ulutas B,Kaynak O.Grey system theory-based models in time series prediction[J].Expert Systems with Applications,2010,37（2）：1784-1789.

[12] 莫国良,吴琳聪,周艳.利用二阶方向导数证明极值的充分条件[J].高等数学研究,2011,14（2）：571-576.

MO Guo-liang,WU Lin-cong,ZHOU Yan.Second order directional derivatives and the second partial derivative test[J].Studies in College Mathematics,2011,14（2）：571-576.（in Chinese）

[13] Xie N M,Liu S F.Discrete grey forecasting model and its optimization[J].Applied Mathematical Modeling,2009,33（2）： 1173-1186.

[14] 刘瑞元.加权欧氏距离及其应用[J].数理统计与管理, 2002,21（5）：1216-1225.

LIU Rui-yuan.Euclid distance with weight and its applications[J]. Application of Statistics and Management,2002,21（5）：1216-1225.（in Chinese）

[15] 张丽丽,殷峻暹,侯召成.基于模糊隶属度的白洋淀生态干旱评价函数研究[J].河海大学学报：自然科学版,2010, 38（3）：1143-1149.

ZHANG Li-li,YIN Jun-xian,HOU Zhao-cheng.Ecological drought evaluation function of Baiyangdian based on fuzzy membership degree[J].Journal of Hohai University：Natural Sciences,2010,38（3）：1143-1149.（in Chinese）

Failure Prediction of Missile Equipment Based on Data Fusion and AMUGM（1,1）Model

ZHAO Jian-zhong1,YE Wen1,ZHANG Lei2
（1.Department of Ordnance Science and Technology,Naval Aeronautical and Astronautical University,Yantai 264001,Shandong,China； 2.Department of Scientific Research,Naval Aeronautical and Astronautical University,Yantai 264001,Shandong,China）

In view of the unequal data sampling time interval,the great difficulty of date sampling and a small amount of data in failure prediction of missile equipment,a prediction method based on data fusion and amendatory metabolism unequal interval grey model（AMUGM（1,1））is proposed according to data fusion technology and grey prediction theory.The unequal interval grey model（UGM（1,1））is established by improved initial value choice and background value constitution,and is optimized by residual error correction and metabolism.Then a membership grade weighted method is put forward based on weighted idea so as to determine the membership values of the models.Finally,a failure prediction model of special individual is built on the basis of membership values and AMUGM（1,1）model.The simulation result shows that the proposed method is effective.

ordnance science and technology；failure prediction；grey model；unequal interval grey model；data fusion

TP391.9

A

1000-1093（2014）10-1689-07

10.3969/j.issn.1000-1093.2014.10.025

2014-01-17

赵建忠（1978—）,讲师,博士。E-mail：zjznavy@163.com；叶文（1979—）,副教授,博士。E-mail：yw97112@sohu.com