超声横向激励下轴向运动金刚石线锯振动切割分析

李伦,李淑娟,汤奥斐,李言

（1.西安理工大学机械与精密仪器工程学院,陕西西安 710048；

2.河南科技大学河南省机械设计及传动系统重点实验室,河南洛阳 471023）

超声横向激励下轴向运动金刚石线锯振动切割分析

李伦1,2,李淑娟1,汤奥斐1,李言1

（1.西安理工大学机械与精密仪器工程学院,陕西西安 710048；

2.河南科技大学河南省机械设计及传动系统重点实验室,河南洛阳 471023）

金刚石线锯由于切缝窄、柔性好而广泛应用于Si、SiC等超硬脆材料的切割过程中,而超声振动在硬脆材料加工方面具有独特的优势。将超声振动应用于线锯切割过程中,在分析轴向运动弦线振动模型的基础上,利用变量分离求解出线锯在两种不同位置超声激励下横向受迫振动位移场的函数表达式以及线锯系统自然频率的函数表达式；研究讨论了线锯系统的参数对固有频率的影响；分析了线锯临界速度以及线锯往复切割时线锯中点振幅与超声激振线锯系统参数的关系；提出了工件进给速度是影响超声振动线锯切割模式的决定因素。用多普勒激光测振仪对线锯的固有频率、线锯超声激励频率和在振动切割SiC中线锯不同点处的频率进行测定,并对线锯施加超声和不施加超声切割SiC进行了对比实验。结果表明超声振动切割能减小23%～38%的切割力,能明显改善切割表面的质量。测定和实验结果与模型分析有较好的一致性。

机械制造工艺与设备；金刚石线锯；超声波激励；受迫振动响应；振动切割；对比切割实验

0 引言

自20世纪90年代以来,线锯加工由于翘曲小、厚度均匀和切口损耗小等特点,已广泛应用到单晶半导体、玻璃和宝石等硬脆材料的切割加工中[1]。超声复合线锯切割技术是利用固结金刚石颗粒的线锯和被加工材料之间相对高速运动的同时,给线锯附加一超声振动,迫使线锯和加工材料由连续接触变为间断接触,使线锯在高频振荡条件下对工件进行切割、摩擦和冲击,以实现材料的去除。超声复合线锯在加工硬脆材料方面有独特的优势,如切割效率高、变形小、切割表面质量好和线锯使用寿命长等特点[2]。Zhou采用单点金刚石刀具车削玻璃时发现,当施加超声振动后,玻璃的加工过程由塑性到脆性转换的临界切割深度变大,使得玻璃的塑性加工更容易实现[3]。孟剑峰[4]把随机切割力作为线锯的激励力,利用Hamilton原理研究了线锯的随机振动,分析了环形电镀金刚石线锯切割硅时加工参数对晶片质量的影响。张辽远等[5-6]利用自制的实验设备使金刚石线锯在纵向超声振动激励下对切割加工脆性材料进行了研究,结果表明,纵向超声振动加工与相同条件下的普通加工相比,具有材料去除率高、表面质量好、破碎小等特点。上述研究仅限于随机力对线锯的振动影响和纵向超声振动对线锯振动影响的研究,而线锯在横向超声激励下受迫振动的研究未见报道。因此,本文以横向超声激励下轴向运动线锯受迫振动的模型为基础,采用理论分析和实验的方法,研究了线锯在横向上施加高频受迫振动的响应、固有频率、临界速度以及实现往复切割时线锯中点的振幅与系统激励参数间的关系,对横向超声振动线锯的切割条件进行了分析,探讨了超声振动线锯切割模式的影响因素。为进一步研究金刚石线锯在横向超声激励下高速、高质量切割SiC等硬脆材料的切割机理提供理论参考依据。

1 金刚石线锯横向激励振动动力学方程

1.1 线锯横向振动微分方程

轴向运动连续体的振动可分为运动弦线的横向振动和运动梁的横向振动[7]。由于线锯的抗弯模量和线密度都很小,因此横向超声波激励下轴向运动线锯的受迫振动可简化成轴向运动弦线在横向激振下的振动[8-9]。

设线锯沿x轴方向以速度v作匀速运动,两端为导轮支撑,张紧力为F,锯丝线密度为ρ,跨距为L,如图1所示。线锯可以简化为一根弦线,O和O′为切割过程中的两个支撑导轮,弦线在Oxy平面内振动,在时刻t,弦线在x轴上任一点x处的偏离平衡位置的横向位移用y表示,y是横坐标x和时间t的函数,即y=y（x,t）.

图1 轴向匀速运动弦线的振动模型Fig.1 Vibration model of string uniformly moving in axial direction

轴向匀速运动线锯可看作是其坐标系随同弦线并按照相同的轴向运动速度v进行同步运动的弦线系统,则同步运动坐标系下的轴向运动线锯的振动可视为两端固定的弦线振动,其横向振动的动力学方程可参照经典固定弦线横向振动的动力学方程,可表示为

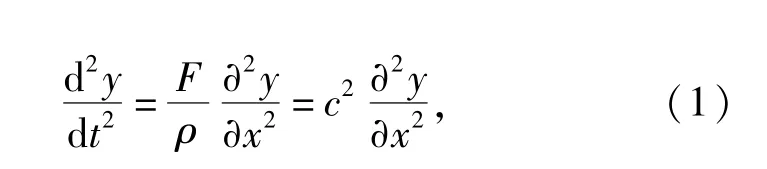
式中：c为横波在固定弦线上的传播速度；F为弦线承受的张紧力；ρ为弦线的线密度；且c=F/ρ；d/dt为坐标系统随着弦线按照速度v同步运动系统对时间的微分算子。运动坐标系与固定坐标系之间在轴向运动速度上存在着下述关系[9]：

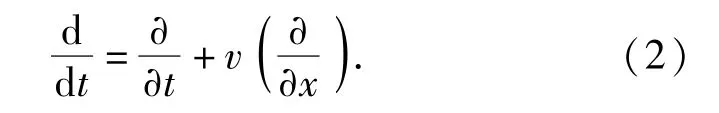
按照（2）式可以把在运动坐标系统的弦线振动的微分方程转换成固定横坐标系统的微分方程。（1）式的左边可表示为参考坐标系统运动速度v对弦线上横向振动波传播速度的影响[10],（1）式的右边则为

由（3）式、（4）式得轴向匀速运动弦线的横向振动方程为

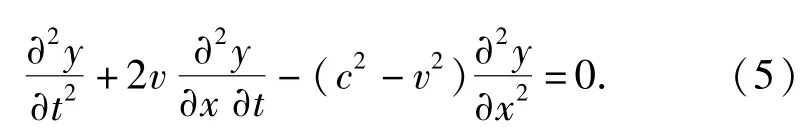
1.2 超声施加位置对运动弦线横向振动的影响

当在轴向运动弦线的右支撑端（O′端）处受到一超声简谐振动y（t）=Acos（ωt）激励时（A为超声波振幅,ω为超声波频率）。此状态相当于线锯往复切割硬脆材料时的反向切割,即线锯上横向振动波的传播方向与线锯的运动方向相反。则此状态振动微分方程（5）式的边界条件为

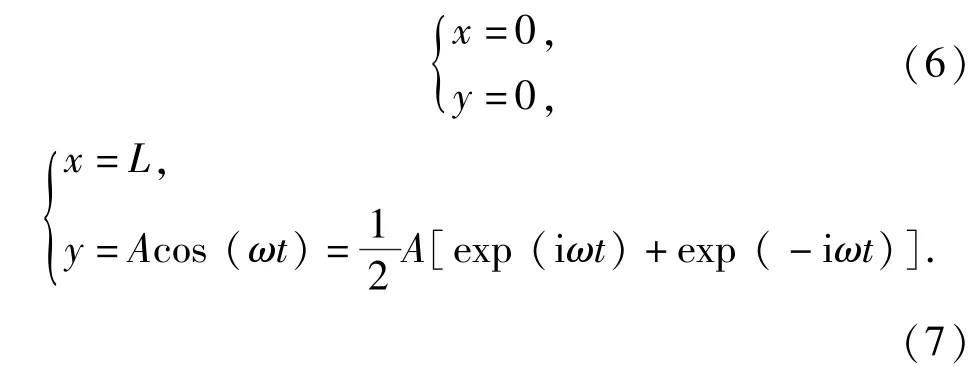
当锯丝是微幅振动,横向振动幅值很小,且弦线的轴向运动速度远小于波在弦线上的传播速度时,可认为系统是线性振动[8]。无阻尼振动微分方程（5）式的解可分解成振型函数和弦上各点位移随时间变化规律函数的乘积[11],设（5）式通解的型式为

式中：v′为弦线运动平均有效速度；c′为运动弦线上平均有效波速。故（5）式通解可表达为

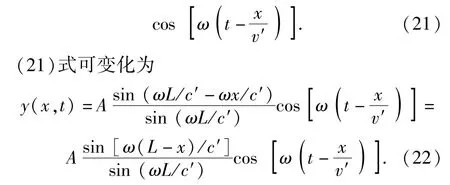
（22）式与（16）式具有相同的结构。当（16）式和（22）式第一项的分子sin（ωx/c′）=0或sin[ω· （L-x）/c′]=0时,弦线的振幅恒为0,此时x点即为驻波的节点。当K的分母sin（ωL/c′）=0时,弦线的振幅为无穷大,即弦线发生共振。当x=L/2时,（16）式和（22）式具有完全相同的解。

1.3 运动弦线固有频率和临界速度

在（16）式和（22）式中,当振幅放大系数K的分母为0时,弦线上振动响应的振幅y→∞,即表示弦线发生了共振,此时激振频率应等于弦线的固有频率[12]。弦线发生共振的条件是sin（ωL/c′）=0,即由（25）式可知,系统每阶固有频率随着轴向速度的增加而减小[13]。当速度达到一定值时,即v=此时,线锯的临界速度为

临界速度的物理意义是指在横向受迫振动中,轴向运动锯丝在横向能发生简谐振动所对应轴向运动速度的最大极限值。当锯丝的轴向运动速度大于等于此极限值时,锯丝的振动频率小于等于0,此状态下锯丝的横向运动将呈现混沌或分岔等不稳定现象,这对于横向振动线锯的切割状态产生不利的影响。

若锯丝选不锈钢材料（牌号0Cr26Ni5Mo2）,锯丝直径d=0.2 mm,线密度ρ=0.245×10-3kg/m,两支撑导轮之间的距离L=0.17 m,线锯轴向运动速度v=1.9 m/s,取线锯张紧力F=28 N,则系统的一阶固有频率（基频）计算值为994.3 Hz.

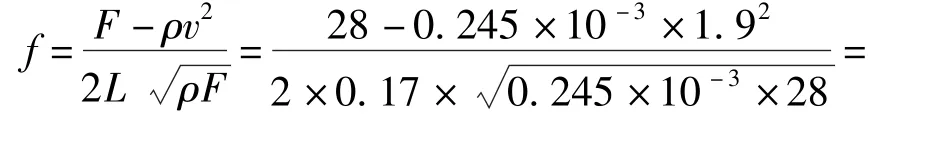
线锯的临界速度为

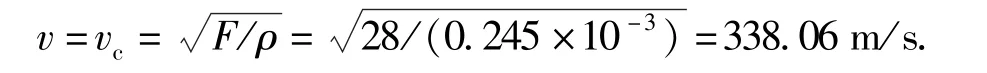
由此可以看出轴向运动弦线的临界速度比较高,而实际上在用线锯切割硬脆材料时,线锯的速度一般不超过20 m/s,远小于线锯的临界速度,因此线锯不会发生分岔失稳现象。

2 超声振动线锯的锯切条件

文献[14]认为：刚性刀具超声振动切割工件时,要实现刀具与工件之间的振动切削,就必须使工件的进给速度vw小于刀具在切削方向上的最大振动速度Aω.即

式中：f为超声波频率；A为振幅。当vw越接近vx,就越接近传统切割。当vw＞vx时,刀具与工件不能分离,不能实现振动切割。

当运动线锯受到横向超声振动激励时,由上述分析可知,线锯中间点的振动为余（正）弦的简谐振动。但该结论是在线锯无负载条件下获得的结果,同时由于线锯切割是柔性切割,柔性线锯上的磨粒对工件的切割不同于刚性刀具的切割,仅满足（27）式还不能保证线锯的振动切割。因此柔性线锯振动切割工件时加工参数必须满足更苛刻的条件,否则线锯即使在超声振动激励下也不能对工件进行振动切割。

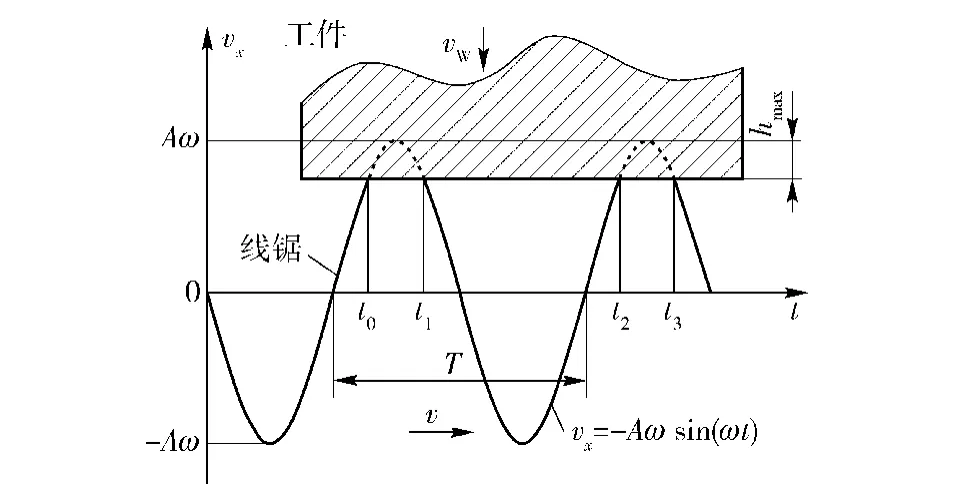
图2 横向超声振动金刚石线锯锯切SiC过程示意图Fig.2 The schematic diagram of cutting process of SiC

图2为柔性线锯对工件振动切割过程示意图。要使柔性线锯能进行振动切割,还必须使工件在一个超声振动周期内的进给量不大于线锯在一个振动周期内的最大切割深度,这样在稳定切割时线锯的平衡位置与工件切割表面间的距离始终保持大于0且小于线锯振幅的稳定状态,以保证线锯的平衡位置在切割平面内保持直线,而不至于发生弯曲,实现线锯对工件的振动点切割。由于振动线锯对旋转工件的切割是振动的点接触,故有

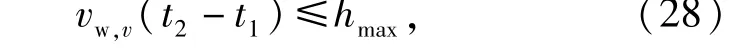
式中：hmax为线锯上磨粒一个周期内的最大切削深度,它与线锯的线质量密度、超声振幅、磨粒的形状、线锯上磨粒的密度、一个振动周期内的净切割时间和锯切材料的断裂韧性有关。vw,v为线锯振动切割时工件的进给速度,t2、t1分别为线锯与工件的接触分离时刻。（28）式即为柔性线锯进行振动切割的条件。

根据（16）式、（22）式,设线锯在L/2处磨粒的振动响应方程为

图2中,t0为线锯与工件的接触时刻,t1为线锯与工件的分离时刻,当线锯与工件分离时即有vw≤vx.

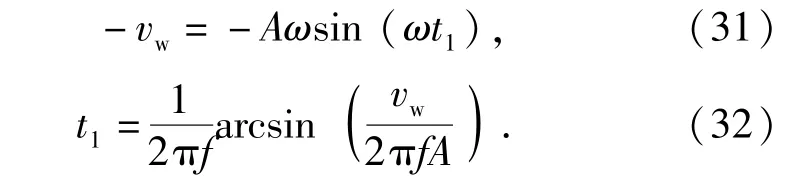
在t1后,在任意时刻t,线锯的中间切割点与工件之间的距离为

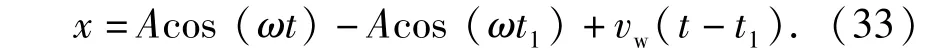
由（33）式可知,当x=0时,线锯再次与工件接触,此时的时刻为t2.则有

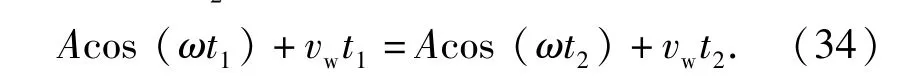
由（31）式和（34）式可解得接触时刻t2、分离时刻t1和超声振动周期T之间的关系：

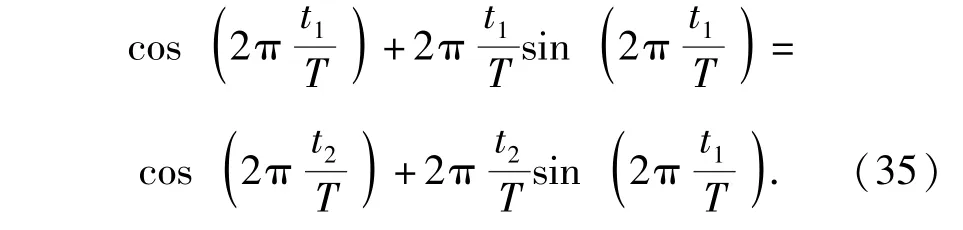
在一个振动周期内线锯切割点参与切割的净切割时间为

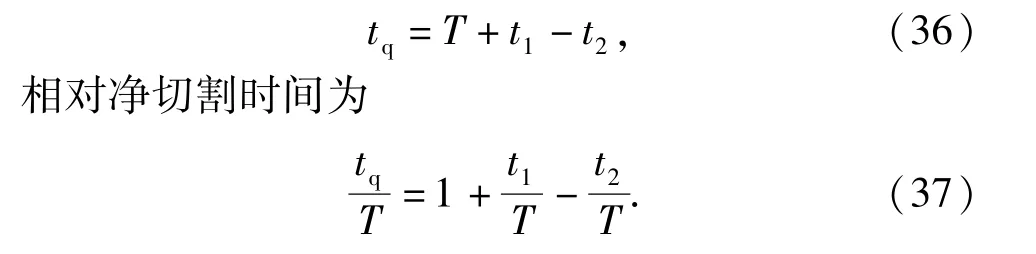
3 实验测试

实验在改进的WXD170型往复式金刚石线锯旋转点切割机床上进行,线锯为不锈钢丝（牌号0Cr26Ni5Mo2）,直径d为0.2 mm,线锯所受张紧力F为28 N,线锯两导轮间距L为170 mm,线锯速度v为1.9 m/s.选用ACQ-600型超声波发生器作为激振源,超声频率为20±1 kHz,振幅为1.285 μm.工件SiC采用PVT法生成,直径为50 mm.线锯沿（0001）晶面进行切割,晶片厚度0.8 mm.

3.1 线锯振动频率及振幅的测定

用LV-S01型多普勒单点激光测振仪对线锯中点的振动进行测试。实验在锯丝静止、锯丝运动和锯丝运动时加超声3种工况下进行,实验测试结果见表1.图3为测试现场照片,图4和图5为锯丝在静态和超声激励下轴向运动线锯的幅频特性测试曲线。

表1 测试结果表Tab.1 The testing results

3.2 超声振动对SiC切割影响的对比实验

图6为对比切割实验原理简图。工件通过两种不同进给速度和在施加超声和不加超声的情况下对线锯的锯切力进行测试,并对切割后的表面进行观察。同时对线锯中间切割点上下各40 mm处的B、C两点处进行振动频率和振幅测量。实验条件：v= 1.9 m/s,nw=12 r/min,A=1.285 μm,冷却液为水。采用美国ATI公司Gamma SI-32-2.5多轴力/扭矩传感器、美国NI公司9105-M1USB 16通道数据采集系统对切割力进行测量。实验结果见表2,表中Ft为切向锯切力,Fn为法向锯切力。

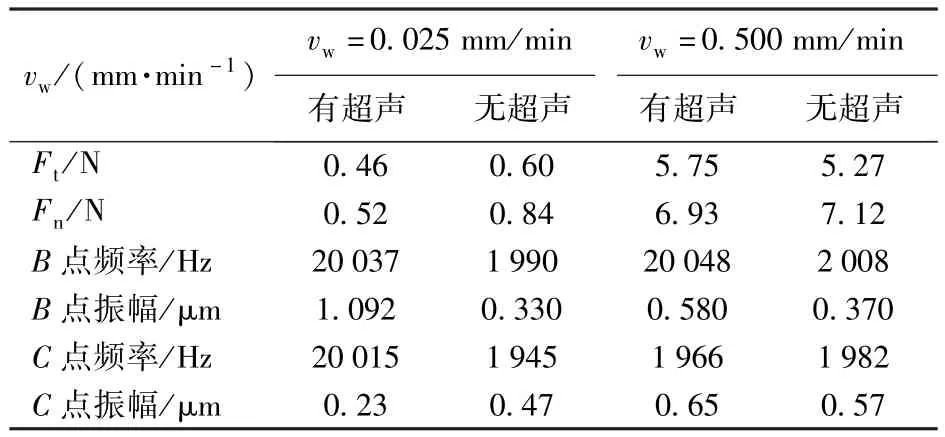
表2 对比切割实验结果Tab.2 Ccutting experiment results

图3 测试现场图片Fig.3 Photograph of test site

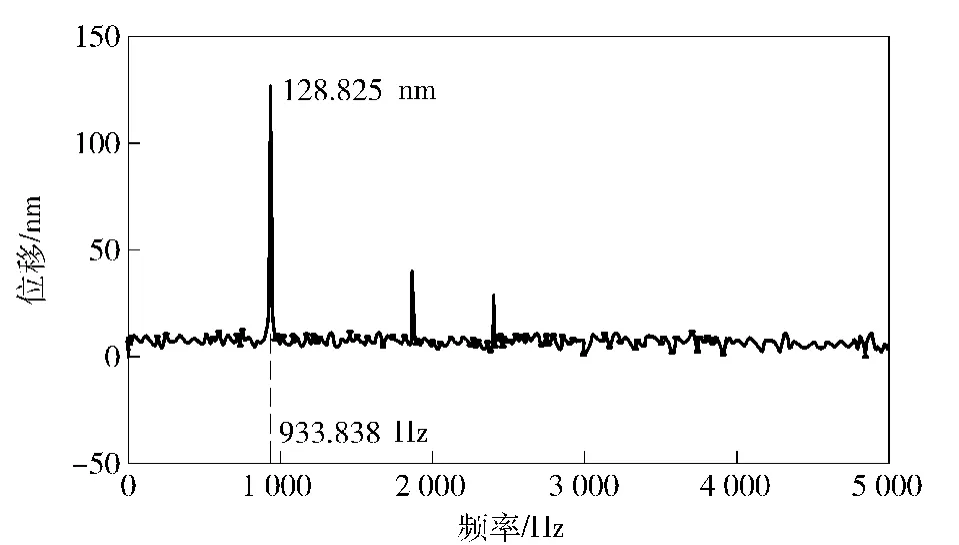
图4 静态线锯幅频曲线Fig.4 Amplitude-frequency curve of wire saw in static state

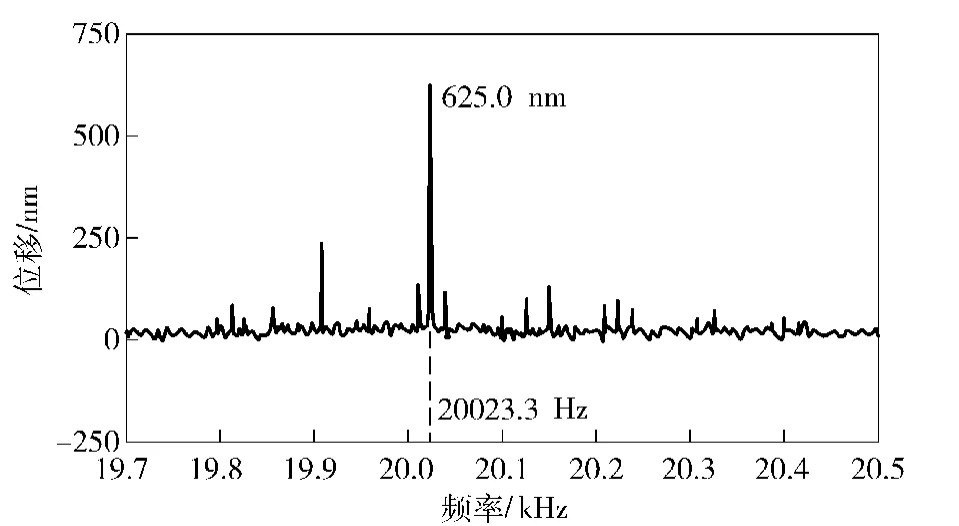
图5 超声激振线锯幅频响应曲线Fig.5 Amplitude-frequency response curve of wire saw excited by ultrasonic transverse vibration

用JSM-6700F场发射扫描电子显微镜（SEM）对切割表面进行晶片表面形貌观察,如图7所示。

4 振动模型及实验结果分析

4.1 超声激振点对线锯中点振幅的影响

由（16）式和（22）式可知,超声激励无论在右端或左端,弦线中间点处的振动位移和相位都是相同的。因此在线锯切割硬脆材料过程中,当工件位于线锯的中间点时无论正向或反向切割,超声振动对工件切割的影响都是相同的。为了使弦线中间点处振幅等于超声激振的振幅A,则

图6 切割实验原理简图Fig.6 Schematic diagram of cutting experiment

图7 超声和普通切割SiC表面SEM形貌对比图Fig.7 Comparison of SEM microscopic topographies ofultrasonically and ordinarily cut SiC surfaces

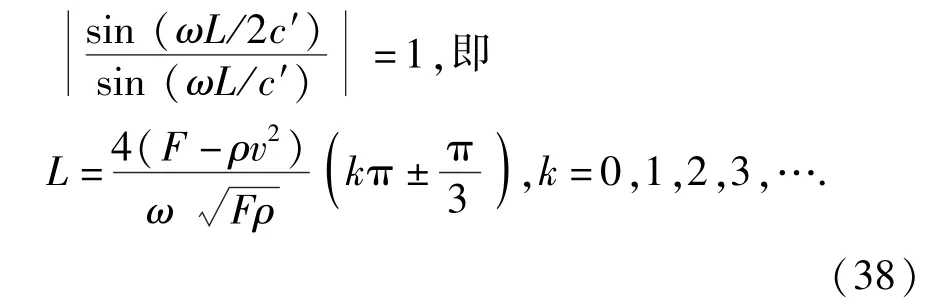
如采用上述实验中的参数值,当k=1时,L应为283.2 mm.

4.2 线锯的临界速度

由（25）式可知：

1）锯丝的振动频率与锯丝的张紧力F有关,在满足锯丝强度条件下增大张紧力F,可增大锯丝固有频率,但过度增加张紧力,会增大线锯的横向刚度。

3）锯丝的固有频率与两个导轮之间跨距L呈反比。

4.3 线锯固有频率测量误差

计算线锯静态一阶固有频率为994.3 Hz,而实验测定线锯静态下的固有频率为933.8 Hz,二者的误差为6.47%.线锯的切割速度为1.9 m/s时,计算频率与测试频率的误差为7.07%.当线锯在超声激励下,锯丝中间点的振幅测量值与计算值的误差为4.53%.这说明建立的线锯振动模型与实际比较一致。产生误差的主要原因是在建立线锯模型时忽略了锯丝的阻尼以及测试过程中环境因素的干扰；同时也说明随着线锯速度的提高,系统的非线性成分也随之增加,导致误差增加[15]。但线锯在远小于临界速度的范围内,采用上述模型可以满足要求的精度。

4.4 线锯切割模式影响因素

线锯在超声激励下能否对工件进行振动切割取决于工件的进给速度,当工件在一个振动周期内的进给量小于线锯在一个振动周期内的最大切割深度时,线锯会进行振动切割,否则即使有超声激励,线锯也不能产生振动切割。当工件进给速度定为0.025 mm/min和0.500 mm/min,可以计算出点切割每个振动周期内,线锯的切削深度分别为0.02083 nm和0.417 00 nm.从B、C两点测试的振幅频率来看,当工件进给速度为0.025 mm/min时,B、C两测试点的频率几乎等于超声振动频率,说明超声振动在线锯的切割过程中能在两导轮之间的线锯上进行传播,而两测试点的的振幅相差较大,说明线锯在振动切割时,线锯上的磨粒对工件切割表面的高频撞击使线锯的振动能量减小,促使材料的去除,从而导致B、C两点的振幅相差较大。同时在实验中观察到线锯在整个切割过程中始终保持直线状态,这说明在上述实验条件下,工件进给速度为0.025 mm/min时,超声激励线锯对工件的切割是振动点切割。

当工件进给速度为0.500 mm/min时,测得的B点的频率与超声频率接近,C点的频率与线锯的2倍基频接近,同时B、C两点的振幅几乎没有明显差别,同时观察到在稳定切割过程中,线锯与工件的接触处发生了明显的弯曲,即由起初的点接触逐渐变成了圆弧线接触。这说明在超声振动线锯切割时,工件的进给速度大于振动周期内磨粒的切割深度,线锯在切割平面内发生弯曲变形,使点接触切割变成了线接触切割,超声振动不能在锯丝上传播,当超声波沿线锯传播到与工件接触段即被工件的弹性形变所吸收,此时线锯受到较大的法向力,因此线锯和工件不会发生周期性的接触-分离,而始终保持圆弧接触状态。在此进给速度下线锯即使有超声激励,线锯也不是超声切割。与普通切割相比,锯切力没有明显的差别。

上述两组实验除了工件进给速度不同外,其余条件均相同,但实验测试和观察的结果不同,当工件进给速度为0.025 mm/min时,为超声振动切割,当进给速度为0.500 mm/min时为普通切割。而线锯的横向最大振动速度计算值为161 mm/s（vx,max= 2πfA）,而上述两组实验工件的进给速度都小于此值,但出现的切割模式却不同,这说明柔性线锯能进行振动切割的条件比刚性刀具的振动切割条件更严格。

上述SiC切割实验也说明磨粒在一个振动周期内的最大切割深度在0.02083 nm和0.41700 nm之间,要准确找到此值,需要从大量的振动切割实验中分析找出,这也是课题今后的研究方向。

4.5 超声对线锯锯切力的影响

从表2实验结果可以看出,与普通切割相比,振动切割使线锯的法向力和切向力明显减小（法向力减小近38%,切向力减小23%）,这主要是受迫振动线锯上的磨粒周期性的撞击、摩擦、切割工件表面,加速材料的去除。这不但提高了材料去除的效率,也减小了线锯的磨损,延长了线锯的寿命。在其他条件相同的情况下,超声振动切割明显改善了晶片表面的质量。

5 结论

1）轴向运动弦线在右端或左端受到简谐振动激励时,弦线的振型都是以轴向速度为v运动的驻波,在弦线的中间点具有相同的振幅和相位。这说明线锯正向或反向切割对硬脆材料的切割机理和切割质量不会产生明显的差异。当满足（38）式时,弦线中间点的振幅与激振振幅相等。锯丝振动的固有频率只与锯丝的线密度、张紧力、速度和跨距有关,与超声激励的位置无关。

2）通常线锯张紧力较大,线锯线密度很小,因此线锯的临界速度很大。在上述条件下计算弦线的临界速度为338.06 m/s,在常规速度切割中（切割速度不大于20 m/s）,线锯不会出现分岔不稳定现象。

3）工件的进给速度对超声振动线锯的切割模式有决定性的影响。当工件在一个振动周期内的进给量小于线锯在一个振动周期内的最大切割深度时,线锯会进行振动切割,否则即使有超声激励,线锯也不是振动切割。

4）超声振动在金刚石线锯往复切割硬脆材料过程中具有显著的作用,不但能减小线锯的锯切力,而且还能增大切割效率,改善表面质量,减小线锯的磨损并延长线锯的寿命。

（References）

[1] Hardin C W,Qu J,Shih A J.Fixed abrasive diamond wire saw slicing of single-crystal silicon carbide wafers[J].Materials and Manufacturing Processes,2004,19（2）：355-367.

[2] 曹凤国.超声加工技术[M].北京：化学工业出版社,2004.

CAO Feng-guo.Ultrasonic machining technology[M].Beijing： Chemical Industry Press,2004.（in Chinese）

[3] Zhou M.Brittle-ductile transition in the diamond cutting of glasses with the aid of ultrasonic vibration[J].Journal of Materials Processing Technology,2002,121：243-251.

[4] 孟剑峰.环形电镀金刚石线锯加工技术及加工质量研究[D].济南：山东大学,2006.

MENG Jian-feng.Research on processing technology and processing quality of endless electroplated diamond wire saw[D].Jinan： Shandong University,2006.（in Chinese）

[5] 张辽远,贾春德,吕玉山.电镀金刚石线锯的超声纵振动切割加工方法[J].兵工学报,2006,27（5）：899-902.

ZHANG Liao-yuan,JIA Chun-de,LYU Yu-shan.A machining methodonelectroplateddiamondwiresawwithultrasonic vibration[J].Acta Armamentarii,2006,27（5）：899-902.（in Chinese）

[6] 张辽远.电镀金刚石线锯超声波切割实验装置的研制和加工机理的研究[D].长春：长春理工大学,2007.

ZHANG Liao-yuan.Research of processing principle and development of experiment setup for electroplated diamond wire saw with ultrasonic vibration[D].Changchun：Changchun University of Science and Technology,2007.（in Chinese）

[7] Nelson H M.Transverse vibration of a moving strip[J].Journal of Sound and Vibration,1979,65（3）：381-389.

[8] 陈立群,Jean W Z.轴向运动弦线的纵向振动及其控制[J].力学进展,2001,31（4）：535-546.

CHEN Li-qun,Jean W Z.Transverse vibration of axially moving strings and its control[J].Advaces in Mechanics,2001,31（4）： 535-546.（in Chinese）

[9] CHEN L Q,ZhANG W,Jean W Z.Nonlinear dynamics for transverse motion of axially moving strings[J].Chaos,Solitons and Fractals,2009（40）：78-90.

[10] Hedrih K.Transversal forced vibrations of an axially moving sandwich belt system[J].Archive of Applied Mechanics,2008, 78（9）：725-735.

[11] Wickert J A,Mote C D.Current research on the vibrations of an axially moving string[J].Shock and Vibration Digest,1988,20（5）： 3-13.

[12] Oz H R.Current research on the vibration and stability of axially moving materials[J].Journal of Sound and Vibration,2003,259 （2）：445-456.

[13] Wickert J A,Mote C D Jr.Classical vibration analysis of axially moving continua[J].Transactions of the ASME,1990,57（9）： 738-744.

[14] Alao Abdur-Rasheed.A fundamental study of vibration assisted machining[J].Advanced Materials Research,2011,264/265： 1702-1707.

[15] Zhang L,Jean W Z.Nonlinear vibration of parametrically excited moving belt,partⅠ：dynamic response[J].Transactions of the ASME,1990,66（6）：396-402.

Vibration Cutting Analysis of Axially Moving Diamond Wire Saw Excited by Transverse Ultrasonic Wave

LI Lun1,2,LI Shu-juan1,Tang Ao-fei1,LI Yan1
（1.School of Mechanical and Precision Instrument Engineering,Xi'an University of Technology,Xi'an 710048,Shaanxi,China； 2.Henan Key Laboratory for Machinery Design and Transmission System,Henan University of Science and Technology, Luoyang 471023,Henan,China）

The diamond wire saw has been widely used in cutting the hard and brittle materials,such as Si and SiC single crystals,because of its narrow kerf and great flexibility.The ultrasonic vibration has a unique benefit in cutting the ultra-hard and brittle materials.Based on the analysis of vibration model of axially moving string,the expressions of transverse vibration displacement field in which the wire saw is excited in different positions by ultrasonic wave are solved by applying the separation-of-variables method,and the expression of system natural frequency is obtained,too.The effect of wire saw system parameters on natural frequency is discussed.The critical speed of wire saw is analyzed.The relation among the midpoint amplitude of wire saw excited by ultrasonic wave when wire saw reciprocatedly cuts and the parameters of wire saw system is analyzed.It is proposed that the feed speed of workpiece is a decisive factor affecting cutting mode of wire saw excited by ultrasonic wave.Doppler laser vibrometer is used tomeasure the natural frequency of wire saw,the vibration response frequency of wire saw excited by ultrasonic wave,and the frequencies of wire saw in different positions when wire saw cuts SiC ingot with ultrasonic vibration.Comparative experiments of cutting SiC are carried out with and without ultrasonic vibration.The result shows that cutting forces is reduced by 23%～38%with ultrasonic vibration cutting,and the quality of the cut surface is improved obviously.The measurement and experimental results are consistent with the analysis results of model.

manufaturing technology and equipment；diamond wire saw；ultrasonic excitation；forced vibration response；vibration cutting；comparative cutting experiment

TH113.1

A

1000-1093（2014）10-1651-08

10.3969/j.issn.1000-1093.2014.10.020

2013-11-26

国家自然科学基金项目（51175420）

李伦（1969—）,男,副教授。E-mail：lilunxn@163.com；李淑娟（1968—）,女,教授,博士生导师。E-mail：shujuanli@xaut.edu.cn