基于量子遗传的机械故障盲源分离方法研究

李志农,皮海玉,肖尧先

（1.南昌航空大学无损检测技术教育部重点实验室,江西南昌 330063； 2.汕头大学广东省数字信号与图像处理技术重点实验室,广东汕头 515063）

基于量子遗传的机械故障盲源分离方法研究

李志农1,2,皮海玉1,肖尧先1

（1.南昌航空大学无损检测技术教育部重点实验室,江西南昌 330063； 2.汕头大学广东省数字信号与图像处理技术重点实验室,广东汕头 515063）

针对基于遗传算法的机械故障源分离（GA-BSS）方法存在的不足和量子遗传的独特优势,提出了基于量子遗传的机械故障盲源分离（QGA-BSS）方法,并与传统的GA-BSS方法进行了比较。仿真结果表明,提出的方法优于GA-BSS方法,尤其是在快速收敛性方面,避免了GA-BSS方法早熟收敛,同时也大幅度地减少了计算量。将提出的方法应用到轴承故障分离中,能很好地提纯出轴承故障特征。实验结果证明,提出的QGA-BSS方法是有效的。

信息处理技术；量子遗传；盲源分离；故障诊断

0 引言

基于遗传算法（GA）的故障信号盲分离方法[1-3]由于存在计算量大、早熟、收敛速度慢等缺点,使其在故障诊断中的应用受到一定的限制,因此有必要探讨新的基于进化理论的盲分离方法。

量子遗传算法（QGA）主要是由GA与量子计算两部分组成,通过量子计算弥补了GA计算量大、早熟、稳定性差等特点,从而实现了QGA的适应性强、搜索范围更广、优化能力更强等特性。目前, QGA已经在信号处理、数据挖掘、无限通信等领域获得了初步的应用。文献[4]提出了一种求解TSP的QGA.文献[5]将QGA成功地应用到无线电决策引擎中。文献[6]以航迹规划作为目标函数,利用QGA对目标函数进行优化,从而实现了无人飞行器航迹规划最优解的选择。文献[7]将对钢管焊接结构焊缝损伤的识别转化为量子遗传对目标函数的优化问题。文献[8]利用QGA对RBF神经网络进行优化,并应用到热工辨识中。文献[9]将量子遗传应用到k-均值聚类中,克服了传统的聚类方法中聚类数必须事先已知,并且聚类结果对聚类中心选择敏感等不足。文献[10]提出了基于量子遗传的电压控制优化方法。文献[11]给出了一种改进量子旋转门的QGA,提高了算法的收敛性,可以有效地避免算法早熟收敛现象。文献[12-13]在基于量子遗传的盲源分离算法中做了许多具体的、非常有意义的工作,提出了一种基于多宇宙并行QGA和独立分量分析的盲源分离算法,并证明了该算法的收敛性。虽然量子遗传的研究取得了一定进展,也有了一些初步应用,然而量子遗传在机械工程领域的研究仍然处于空白。

针对基于GA的故障信号盲分离方法存在的不足和QGA的独特特性,本文将QGA引入到机械故障诊断中,很好地体现了学科的交叉,并结合盲源分离（BSS）算法,提出了一种基于量子遗传的机械故障盲源分离方法。为便于后面叙述,将本文提出的方法称为QGA-BSS算法。同时为了更好地证明此算法的独特的优良特性,本文还将QGA-BSS算法与基于GA的盲源分离（GA-BSS）算法进行对比分析,最后,将提出的QGA-BSS算法应用到轴承内、外圈故障盲源分离中,实验取得了满意的分离效果。

1 QGA-BSS算法

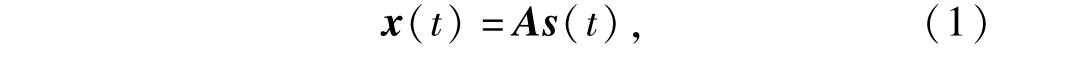
考虑瞬时混合的盲源分离模型式中：s（t）=[s1（t）,s2（t）,s3（t）,…,sN（t）]T为N个独立源信号；x（t）=[x1（t）,x2（t）,x3（t）,…, xM（t）]T为M个传感器所观测到的信号；A为M×N的混合矩阵。盲源分离的目的是寻找一个分离矩阵W,使得估计的源信号向量y（t）中各个分量之间尽可能地独立。

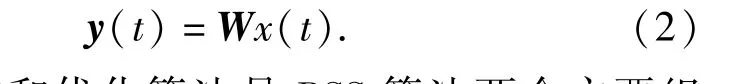
目标函数和优化算法是BSS算法两个主要组成部分。一般地,通过优化某一目标函数来估计BSS模型,亦即有[14]

在BSS算法中,目标函数决定了BSS算法的统计特性（如一致性、渐进方差、鲁棒性）,优化方法决定了BSS算法的性质（如数值稳定性、收敛速度、存储需求）。这里,选取常用的峭度作为目标函数,其定义为

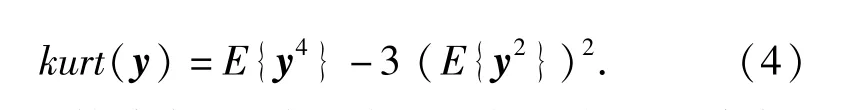
目标函数确定后,接下来就是优化方法的确定。常用的优化方法有共轭梯度下降法和GA。梯度下降法是根据负梯度方向来确定每次迭代的新的搜索方向,达到每次迭代后,待优化的目标函数能逐步减小。但是该方法容易陷入局部最优解。GA基本不用搜索空间的知识或其他辅助信息,而仅用适应度函数值来评估个体,在此基础上进行遗传操作。然而,该方法在编码时不能全面地将优化问题的约束表示出来,而且还具有运行效率低、容易过早收敛等缺点。针对现有的优化算法,特别是遗传优化方法存在的不足,本文将QGA引入到机械故障盲源分离,采用量子遗传来达到优化目标函数的目的。QGA-BSS算法的基本过程如图1所示。

由图1可知,实现该算法流程图的关键要解决3个问题。

1.1 适应度函数的确定

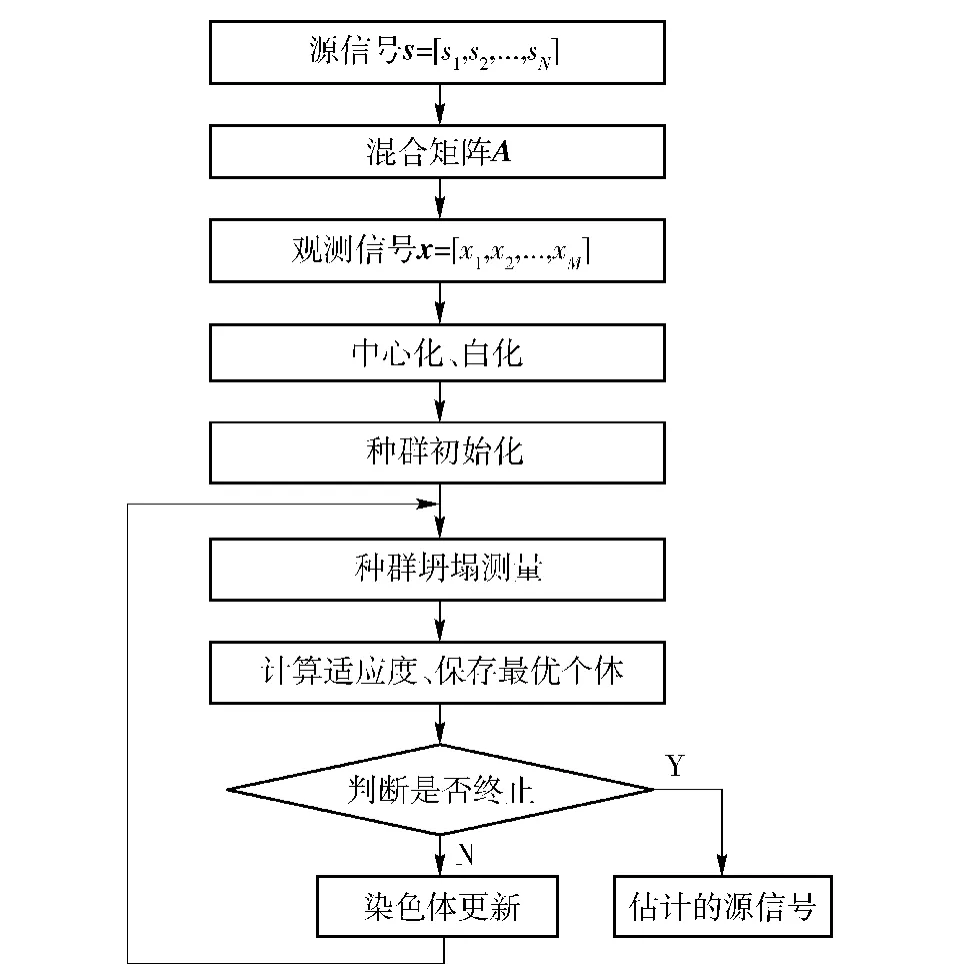
图1 QGA-BSS方法Fig.1 QGA-BSS method

和GA类似,量子遗传进化过程中仍是以适应度函数为依据,根据种群每个个体的适应度来进行搜索。因此,适应度函数的选取会直接关系到QGA的收敛性和是否能找到最优解。在具体选择时,适应度函数应该尽量简单,计算量要小,通用性强,因为适应度函数的复杂度会增加搜索的计算量。另外,在实际工程应用中,常将目标函数映射成求最大值形式而且函数值非负的适应度函数是必要的。

K-L散度、互信息、互熵、峭度都可以作为信号非高斯性的判据。其中,峭度是最简单、最直接定量度量随机信号非高斯性的的判据,而且它计算量小,通用性强。因此,本文选用峭度来作为适应度函数。考虑到处理信号的种类不同,当峭度大于0时,为超高斯信号；峭度小于0时,为亚高斯信号；峭度等于0为高斯信号。因而若单纯处理某种类的信号时可采用峭度进行分离。但是实际处理中一般都是各种信号的混合,只使用峭度是无法准确分离,因而,选取峭度的绝对值就可不用考虑信号的种类而对混合信号直接进行分离。为此,引入峭度的绝对值之和J（y）作为适应度函数,其定义为

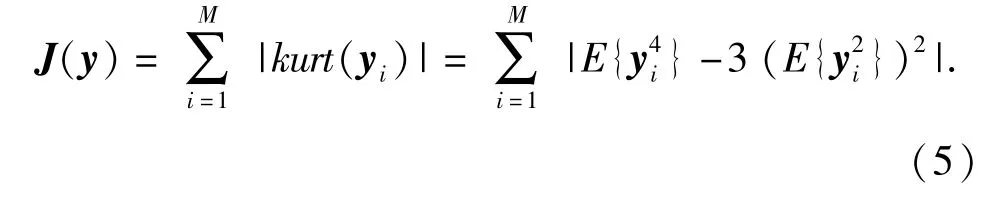
1.2 量子比特编码

在常规的计算中,二进制的0或1常用来表示信息单元。在量子计算中,量子比特是存储信息的最小信息单元,它除了存在于0或1状态之外,还可以存在于二者之间的一种叠加状态。量子态常用狄拉克符号〈|和|〉表示,分别称为左矢和右矢。矢量的标记形式为|θ〉,其中θ可以是字母、数字或者是字。量子比特|φ〉的表示方法为

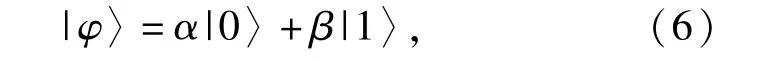
式中：|0〉表示自旋向下态；|1〉表示自旋向上态。量子比特的概率幅值通常用一对复数α、β表示,且它们满足归一化条件

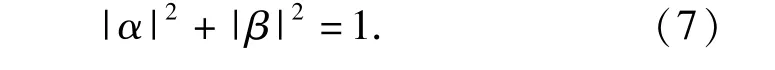
由（6）式和（7）式可以看出,一个量子比特涵盖了一个量子的各种状态。用量子比特表示的染色体叫作量子染色体。

对分离矩阵W编码,在此采用二进制编码,对存在的多态问题,在此,采用串行量子比特编码来处理,如两态可以用一个量子比特来编码,4态可以用两个量子比特来编码,依次类推。这种编码方式简单、易实现,而且通用性强。在本文中是对两个源信号进行分离,分离矩阵为2×2的矩阵。对分离矩阵进行多态量子比特编码。

如图2所示,w11,w12,w21,w22分别用一个16 bit的二进制数表示,则一个量子染色体上含有16× 4=64个量子比特。表示第t代第j个染色体的编码情况,和表示第t代w11的第一个染色体的基因状态,和表示第t代w11的第二个染色体的基因状态,其他符号的含义依次类推。

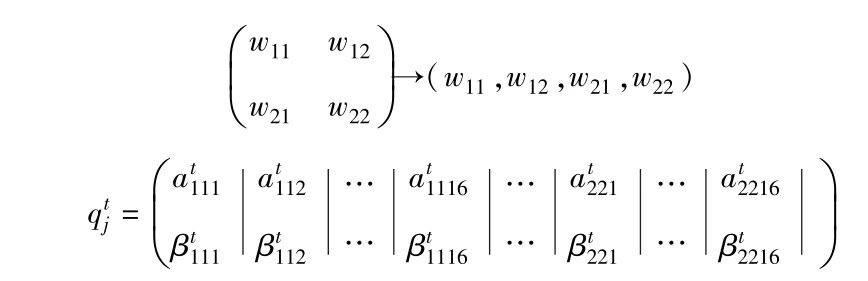
图2 量子染色体编码Fig.2 Coding pattern of quantum chromosome

1.3 量子染色体的演化

在量子计算中,有个很重要的理论是量子门操作。在QGA中,选用量子旋转门来实现对量子染色体的变异,从而加快种群的进化。量子旋转门的调整如（8）式所示：

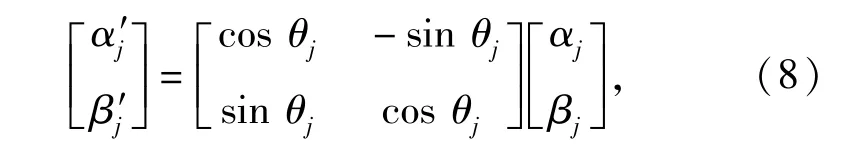
式中：（αj,βj）和θj分别表示量子染色体上的第j位量子比特基因和量子旋转门的旋转角。旋转角的定义为

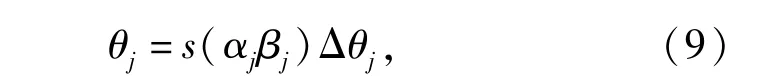
式中：s（αjβj）和Γθj分别表示旋转门的方向和旋转角大小,其大小和方向根据一个事先设计的调整策略而确定。本文采用了文献[13]提出的一种通用的、与问题无关的调整策略。在量子染色体演化过程中,通过量子旋转门来搜寻最佳个体,使得QGA具有全局搜索能力。

这样,由最佳个体的最佳解获取分离矩阵W,从而利用（2）式可以得到源信号的估计。

2 仿真研究

为了验证提出的QGA-BSS算法的有效性,在此,构造如下两个调幅调频信号

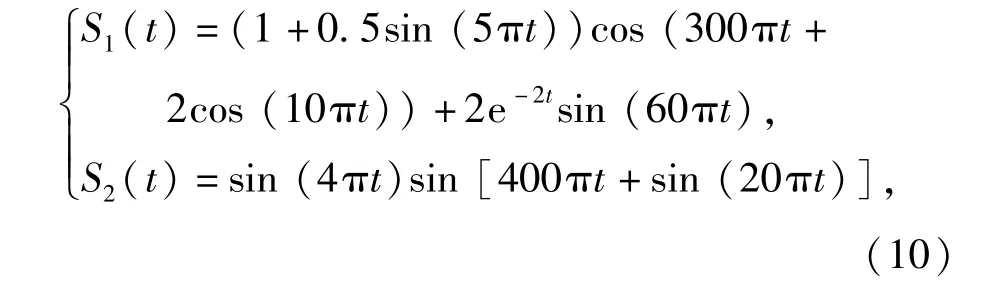
式中：采样频率为512 Hz,采样长度为512个点。源信号波形如图3所示。

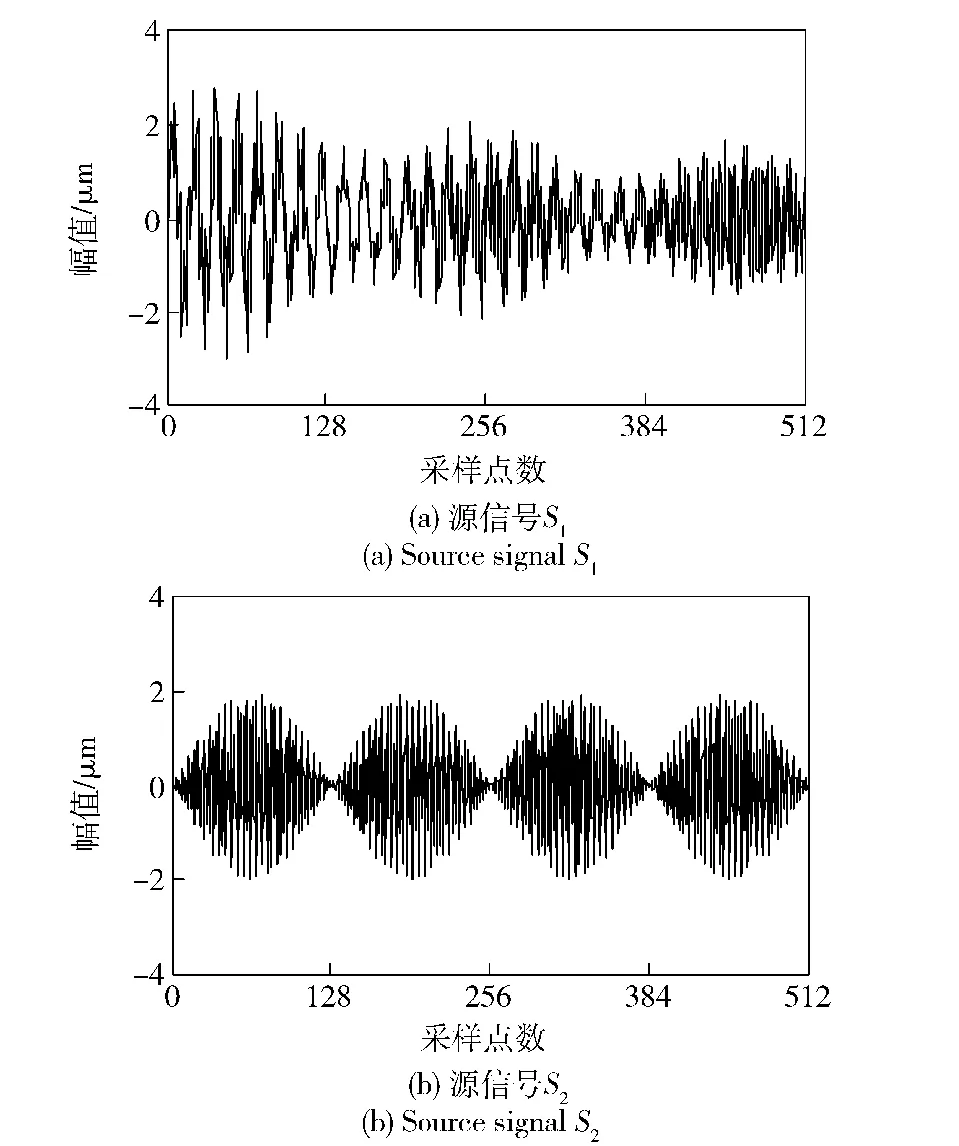
图3 源信号Fig.3 Source signals

为了得到混合信号,这里随机产生一个2×2的混合矩阵A,与源信号相乘得到的混合信号如图4所示。

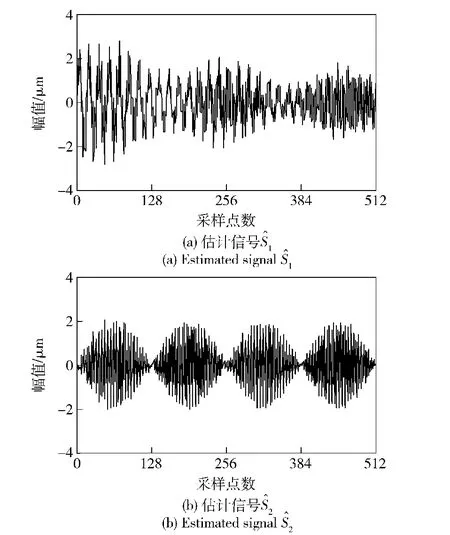
对混合信号采用QGA-BSS算法进行盲源分离,得到的估计信号如图5所示。为了比较,这里还采用GA-BSS算法对混合信号进行盲源分离,得到的估计信号如图6所示。

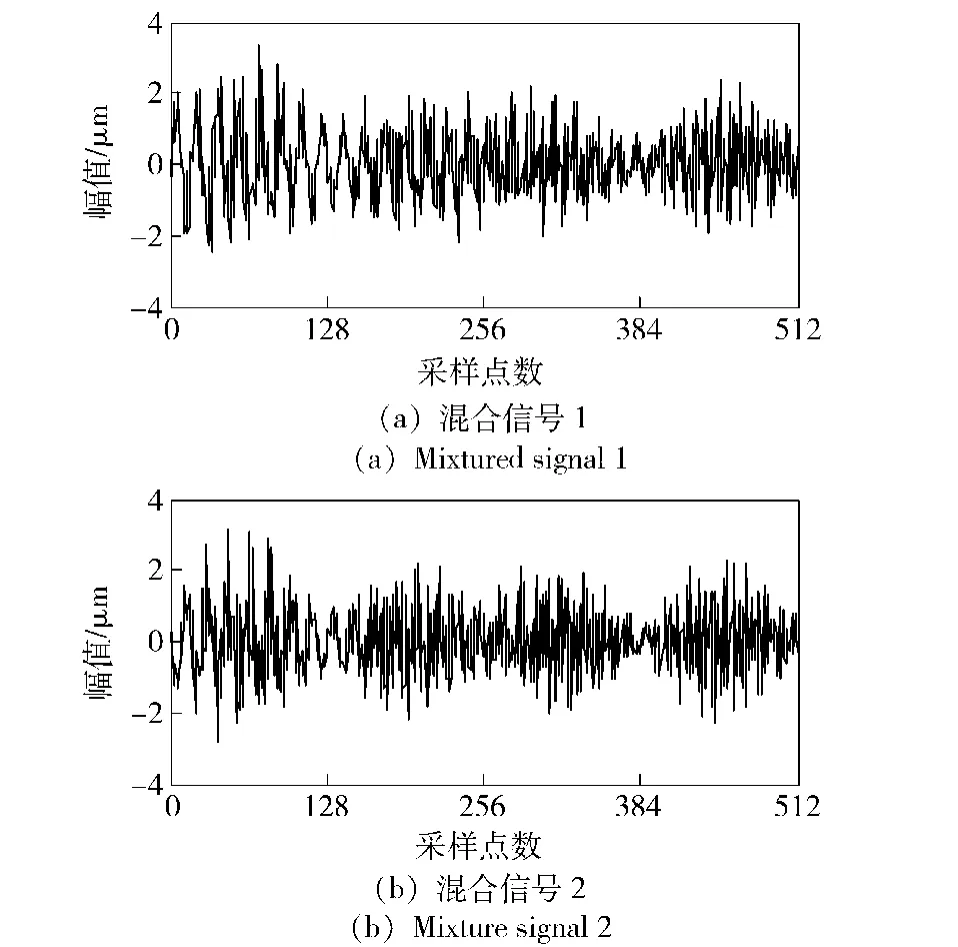
图4 混合信号Fig.4 Mixtured signals

2.1 分离性能比较

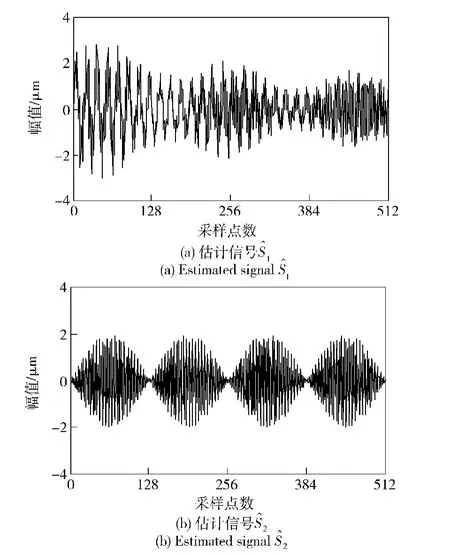
图6 估计信号（GA-BSS方法）Fig.6 Estimated signals（GA-BSS method）

对比图5和图3、图6和图3,无论是用QGABSS方法,还是用GA-BSS方法都能得到满意的分离效果,只不过它们的相位和幅值有些变化。然而,盲源分离中这些固有的不确定性对分离结果的正确性并无影响,因为源信号的信息完全蕴含在信号的波形中。对估计信号进行频谱分析,得到的结果如图7所示。为了更清楚地看到源信号S1的频率成分,在此,将图7（b）中128～175 Hz之间的频率放大,得到的结果如图7（c）所示。

由图7（a）可知,恢复的信号明显反映了源信号S2的频率,由于频率2 Hz和10 Hz的调制作用,在频率178 Hz、182 Hz、188 Hz、192 Hz、198 Hz、202 Hz、208 Hz、212 Hz、218 Hz、222 Hz都出现了峰值。

由图7（b）和图7（c）可知,该波形明显反映了源信号S1的频率结构。在特征频率30 Hz处反映明显。另外,由于5 Hz频率的调制作用,在特征频率130 Hz、135 Hz、140 Hz、145 Hz、150 Hz、155 Hz、160 Hz、165 Hz、170 Hz处也反映明显。同时,由于2.5 Hz的调制作用,在频率157.5 Hz,162.5 Hz, 142.5 Hz等处也出现了峰值,只不过2.5 Hz的调制作用明显比5 Hz的调制作用弱。由此可知,提出的方法很好地把这两个源信号从混合信号中有效地分离出来了。

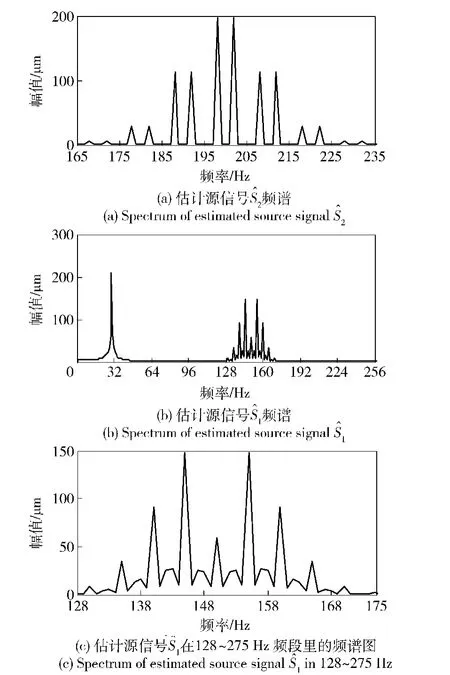
图7 估计信号的频谱Fig.7 Spectrum of estimated source signals

为了比较这两种方法的分离性能,可以采用分离矩阵W与混合矩阵A作乘积得到U=WA来衡量。若U中每行的绝对值最大值与该行的其他值的差异越大,则该算法的分离效果越好。

对于本例,QGA-BSS算法、GA-BSS算法得到的U值分别为

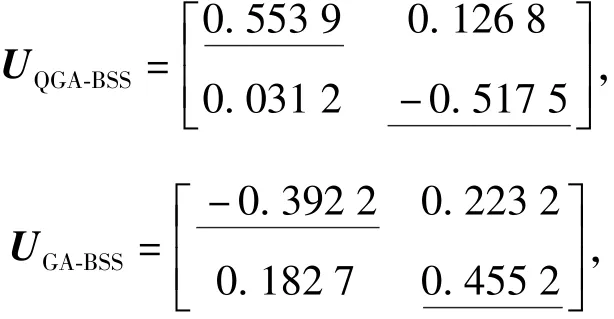
UQGA-BSS、UGA-BSS中每行绝对值的最大值用下划线标出。

对比UQGA-BSS和UGA-BSS,可以发现UQGA-BSS中每行的绝对值最大值与该行的其他值的差异明显远远大于UGA-BSS中每行的绝对值最大值与该行其他值的差异,因而QGA-BSS方法的分离效果还是优于GA-BSS方法。

2.2 算法收敛性和运行速度比较

虽然QGA-BSS方法和GA-BSS方法都获得了满意的分离效果,然而,这两种算法的收敛性和分离速度存在明显的差异。图8给出了QGA-BSS方法和GA-BSS方法寻找到的最优解的收敛曲线图。其中,横、纵坐标分别表示种群进化代数和相应的适应度值。

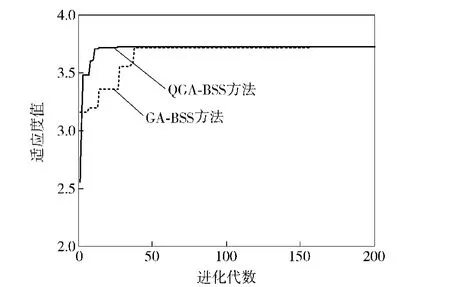
图8 收敛曲线Fig.8 Convergence curves

由图8可知,利用GA-BSS方法时种群大约在40代以后才收敛,找到最优解。而利用QGA-BSS方法时,可以看出种群大约在第15代就开始收敛,并保持稳定。虽然两种方法都能达到最优值,但是QGA-BSS方法的适应度值是随着进化代数的增加而得到改善,种群适应度均值和方差均收敛。由此可知,QGA-BSS方法的收敛性远远优于GA-BSS方法。

在仿真中还发现,达到上述最佳适应度时GA-BSS方法中若需选取50个种群每代需要的时间为63.5 s,而QGA-BSS方法中只需选取6个、10个、20个种群,所耗费的时间分别为4.3 s、6.8 s、13.1 s.由此可见,相比较GA-BSS方法,QGA-BSS方法计算量大幅度缩短,这也更加说明QGA-BSS方法的的优越性。这是因为在QGA-BSS算法中,由于染色体上的基因由量子比特编码,一条长度为m的染色体可以表达2m个状态,而用GA-BSS算法则需要用2m个染色体表达,由此可见QGA-BSS算法大大节省了存储空间,使得其运算时间缩短,运算效率提高。而且用QGA-BSS方法中采用交叉变异并用量子旋转门变异来寻找最优解,避免过早收敛。因此,QGABSS方法明显优于GA-BSS方法。

3 实验研究

为了进一步验证提出的方法的有效性,在此,将提出的方法应用到轴承内外圈故障分离中。实验平台由一个1 492 W的电机,一个扭矩传感器/编码器,一个功率计和控制电路组成。使用电火花加工技术在轴承上布置了单点故障,内圈故障直径为0.18 mm,深度为0.28 mm,外圈故障直径也是0.18 mm,深度为0.28 mm.在实验中,电机转速为1 750 r/min,即轴承基频为fr=29.2 Hz,采样频率为12 kHz,根据轴承几何尺寸和转速,可计算出轴承内圈故障频率fi=157.5 Hz,轴承外圈故障频率为fo= 105.0 Hz.

图9为轴承内、外圈故障同时存在时的所测得的观测信号,利用QGA-BSS算法对该观测信号进行分离,得到的估计信号如图10所示,相应的包络谱如图11所示。

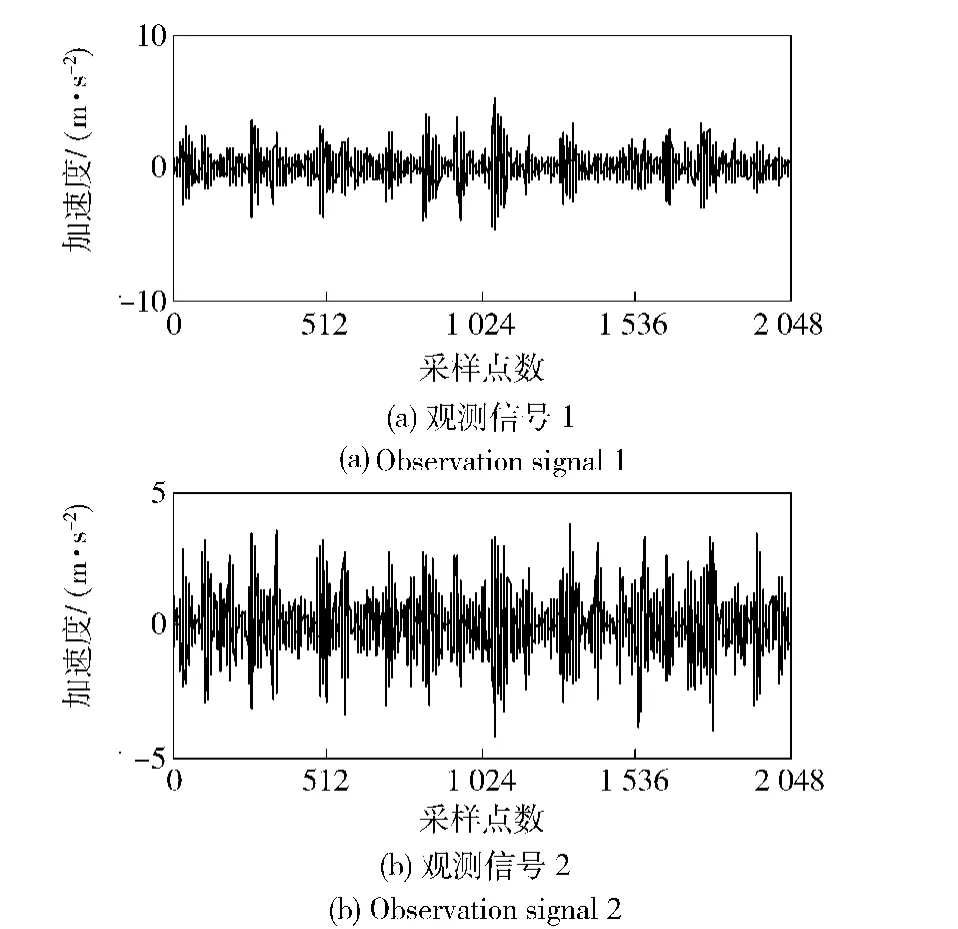
图9 观测信号Fig.9 Observation signals

由图11（a）可知,在频率为157.5 Hz处可以看到明显峰值,正好对应着理论上的轴承内圈故障频率。在频率29.2 Hz、58.4 Hz也出现了峰值,这些峰值对应的频率为转轴频率的基频和2倍频。另外,在频率99.5（fi-2fr）、215.9（fi+2fr）等处也出现明显峰值,这是由于转轴频率的调制作用结果。由此可以看出图11（a）正好反映了以157.5 Hz为特征频率的内圈故障。

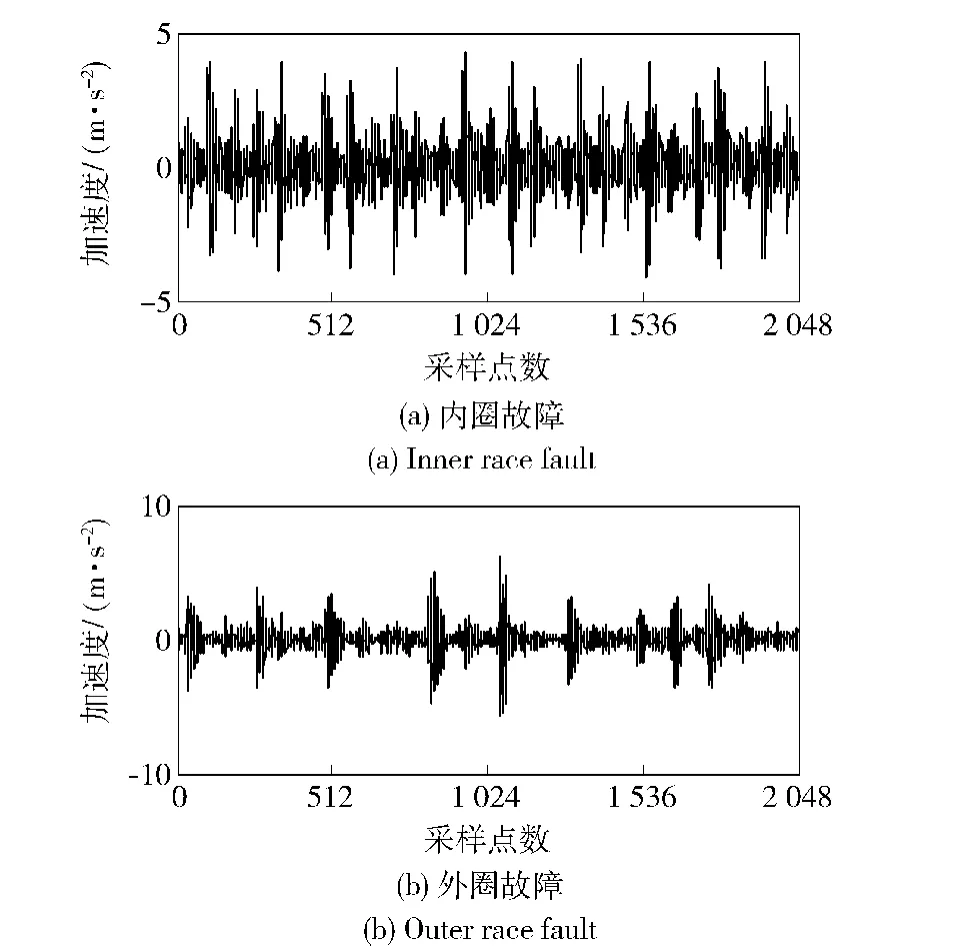
图10 估计信号Fig.10 Estimated signals

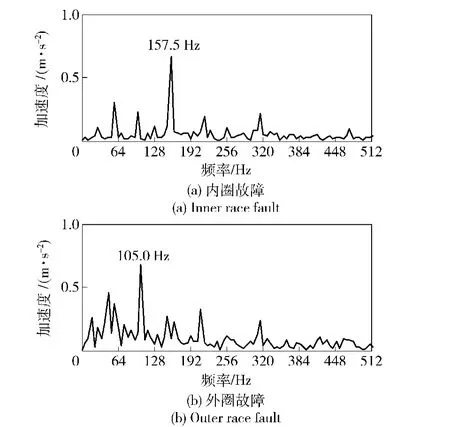
图11 估计信号的包络谱Fig.11 Envelope spectrum of estimated signal

同样,由图11（b）可知,在105.0 Hz处可以看到明显的峰值,和理论上的轴承外圈故障特征频率一致。在29.2 Hz、58.4 Hz处也出现峰值,这些峰值对应的频率正好是转轴的基频和2倍频。同时,在210.0 Hz处出现峰值,这与外圈故障特征频率的2倍频相同。另外,在频率46.6（fo-2fr）、163.4（fo+2fr）处也出现明显峰值,这也是由于转轴频率的调制作用结果。由此可以看出轴承出现了以105.0 Hz为特征频率的外圈故障。

由此可知,QGA-BSS算法能很好地诊断出轴承内外圈故障,从而证明了提出的方法的有效性。

4 结论

QGA是一种具有搜索范围广、优化能力强,并且具有很好应用潜力的进化算法。本文将量子遗传引入到机械故障诊断中,并结合盲源分离,提出了一种基于量子遗传的机械故障盲源分离方法,并对该方法中涉及的关键问题给出了具体的解决方法。同时,提出的方法与GA-BSS方法进行了对比分析。仿真研究表明：两种方法都能得到很好的分离效果。然而,在收敛性和快速性方面存在明显的差别。传统的GA-BSS算法计算量大,占用很大的存储空间,且运行效率低等不足,而QGA-BSS算法中,解空间染色体的量子比特编码方式和量子染色体旋转门的演化机制大大丰富了种群的多样性,同时也大大节省了存储空间和避免了早熟收敛。将QGA-BSS方法应用到轴承内、外圈故障盲分离中,实验结果表明提出的方法是非常有效的,能很好地辨识出故障的频率特征。

（References）

[1] 李良敏.基于遗传算法的盲源分离在轴承诊断中的应用[J].轴承,2005（9）：31-34.

LI Liang-min.Application of blind source separation method based on genetic algorithm in bearing fault[J].Bearing,2005（9）： 31-34.（in Chinese）

[2] 李红亮.基于进化算法的盲源分离研究[D].秦皇岛：燕山大学,2009.

LI Hong-liang.Research of blind source separation method based on genetic algorithm[D].Qinhuangdao：Yanshan University, 2009.（in Chinese）

[3] 易叶青.基于进化算法的盲源分离[D].长沙：湖南大学, 2005.

Yi Ye-qing.Blind source separation method based on evolutionary algorihtms[D].Changsha：Hunan University,2005.（in Chinese）

[4] 王宇平,李英华.求解TSP的量子遗传算法[J].计算机学报, 2007,30（5）：748-755.

WANG Yu-ping,LI Ying-hua.A novel quantum genetic algorithm for TSP[J].Chinese Journal of Computers,2007,30（5）：748-755.（in Chinese）

[5] 赵知劲,郑仕链,尚俊娜,等.基于量子遗传算法的认知无线电决策引擎研究[J].物理学报,2007,56（11）：6760-6766.

ZHAO Zhi-jin,ZHENG Shi-lian,SHANG Jun-na,et al.A study of cognitive radio decision engine based on quantum genetic algorithm[J].Acta Physica Sinica,2007,56（11）：6760-6766.（in Chinese）

[6] 孙阳光,丁明跃,周成平,等.基于量子遗传算法的无人飞行器航迹规划[J].宇航学报,2010,31（3）：648-654.

SUN Yang-guang,DING Ming-yue,ZHOU Cheng-ping,et al. Route planning based on quantum genetic algorithm for UAVs[J]. Journal of Stronautics,2010,31（3）：648-654.（in Chinese）

[7] 王天辉,马立元,李世龙,等.基于量子遗传算法的钢管焊接结构焊缝损伤识别[J].海军工程大学学报,2012,24（6）：89-94.

WANG Tian-hui,MA Li-yuan,LI Shi-long,et al.Damage detection of weld seam damage on steel tube welded structures by quantum genetic algorithm[J].Journal of Naval University of Engineering,2012,24（6）：89-94.（in Chinese）

[8] 董泽,黄宇,韩璞.量子遗传遗传算法优化RBF神经网络及其在热工辨识中的应用[J].中国电机工程学报,2008,28（17）： 99-104.

DONG Ze,HUANG Yu,HAN Pu.Thermal process identification with radial basis function network based on quantum genetic algorithm[J].Proceedings of the CSEE,2008,28（17）：99-104. （in Chinese）

[9] Xiao J,Yan Y P,Zhang J,et al.A quantum-inspired genetic algorithm for K-means clustering[J].Expert Systems with Applications,2010,37：4966-4973.

[10] Vlachogiannis J G,Qstergaard J.Reactive power and voltage control based on general quantum genetic algorithms[J].Expert Systems with Applications,2009,36：6118-6126.

[11] 张小锋,睢贵芳,郑冉,等.一种改进的量子旋转门量子遗传算法[J].计算机工程,2013,39（4）：234-238.

ZHANG Xiao-feng,SUI Gui-fang,ZHENG Ran,et al.An improved quantum genetic algorithm of quantum revolving gate[J]. Computer Engineering,2013,39（4）：234-238.（in Chinese）

[12] 杨俊安,邹谊,庄镇泉.基于多宇宙并行量子遗传算法的非线性盲源分离算法研究[J].电子与信息学报,2004,26（8）：1210-1217.

YANG Jun-an,ZOU Yi,ZHUANG Zhen-quan.Nonlinear blind source separation algorithm using multi-universe parallel quantum genetic algorithm[J].Journal of Electronics&Information Technology,2004,26（8）：1210-1217.（in Chinese）

[13] 杨俊安.基于量子遗传算法的盲源分离算法研究[D].合肥：中国科技大学,2003.

YANG Jun-an.Quantum genetic algorithm and its application research in blind source separation[D].Hefei：University of Science and Technology of China,2003.（in Chinese）

[14] Hyvävinen A,Karhunen J,Oja E.独立成分分析[M].周宗潭,董国华,徐新,等,译.北京：电子工业出版社,2007.

Hyvävinen A,Karhunen J,Oja E.Independent component analysis[M].ZHOU Zong-tan,DONG Guo-hua,XU Xin,et al, translated.Beijing：Publishing House of Electrics Industry, 2007.（in Chinese）

Blind Source Separation of Mechanical Fault Based on Quantum Genetic Algorithm

LI Zhi-nong1,2,PI Hai-yu1,XIAO Yao-xian1
（1.Key Laboratory of Nondestructive Testing,Ministry of Education,Nanchang Hangkong University,Nanchang 330063,Jiangxi,China； 2.Guangdong Key Laboratory of Digital Signal and Image Processing,Shantou University,Shantou 515063,Guangdong,China）

For the deficiency in the blind separation method of mechanical fault sources based on the genetic algorithm,which is named as GA-BSS method,and the unique advantages of quantum genetic algorithm,a blind separation method of mechanical fault sources based on the quantum genetic algorithm, which is named as QGA-BSS method,is proposed.The proposed method is compared with the traditional GA-BSS method.The simulation results show that the QGA-BSS method is superior to the traditional GABSS method,especially in the convergence speed.The proposed method avoids the premature convergence in the GA-BSS method and greatly reduces the amount of calculation.Finally,The proposed method is applied to the separation of bearing fault,and can extract the bearing fault features from the mixture signals successfully.The experimental results prove that the proposed QGA-BSS method is effective.

information processing technology；quantum genetic algorithm；blind source separation； fault diagnosis

TH165+. 3；TN911. 7；TP206+.3

A

1000-1093（2014）10-1681-08

10.3969/j.issn.1000-1093.2014.10.024

2014-01-18

国家自然科学基金项目（51265039、51075372、50775208）；江西省教育厅科技计划项目（GJJ12405）；湖南科技大学机械设备健康维护湖南省重点实验室开放基金项目（201204）；广东省数字信号与图像处理技术重点实验室开放基金项目（2014GDDSIPL-01）

李志农（1966—）,男,教授。E-mail：lizhinong@tsinghua.org.cn；皮海玉（1989—）,女,硕士研究生。E-mail：pihaiyu@126.com