水下爆炸冲击波作用下船体舱段刚体运动试验研究

， ， ，晓强

(1.中国船舶重工集团公司第七〇一研究所军事代表室，武汉 430064;2.哈尔滨工程大学 船舶工程学院,哈尔滨 15001)

舰船在水下爆炸载荷作用下的动力响应通常由两部分组成：刚体运动和弹塑性变形。短而宽的船体和刚度较大的船体在水下爆炸环境中刚体运动显著，而在现有文献的基础上[1～3]，刚体运动的影响一直未被深入考虑。在实际船体抗水下爆炸过程中，刚体运动会吸收相当一部分的爆炸能量，忽略刚体运动会使基于能量方法计算的船体弹塑性响应偏大，难以给出船体弹塑性响应的准确结果。

在水下爆炸时，其载荷主要包括水下爆炸冲击波和气泡脉动。在此过程中压力的变化在所有的实际情况中都有突跃形式，突跃后紧接着近似于按指数规律变化的衰减，衰减时间不超过数毫秒，而在这数毫秒的冲击波中，却包含了爆炸总能量的53%左右。在舰船实尺度舱段试验过程中，发现舱段外板除发生弹塑性变形外，舱段本身在水中也产生了较大的起伏，因此冲击波对舰船的刚体运动作用不可小觑。

关于船体在水下爆炸载荷作用下的刚体运动的研究成果并不是很多。文献[4]研究了水下爆炸球面冲击波作用下的船体梁刚塑性动力响应，是把船体简化为等截面直梁，将球面冲击波简化为移动的平面波进行加载，提出了一种计算船体梁在球面冲击波作用下发生刚体运动或塑性运动的近似理论方法，但未给出适合船体运动速度的预报方法。文献[5]也是将船体简化为船体梁，利用模态叠加法，研究了水下爆炸气泡作用下的船体刚体运动对鞭状运动过程中的影响，但并未考虑冲击波阶段的影响。

为此，重点研究在水下爆炸冲击波的作用下船体的刚体运动，分析船体舱段在水中爆炸发生后的起伏运动，把整个船体舱段的受力模型简化为平板，考虑船体和流场流固耦合作用产生的附加质量，推导平板在水下球面冲击波压力作用下的刚体运动方程，提出冲击波和船体相互作用的理论，对舰船在水下爆炸环境中的刚体运动进行预报，最后通过舰船实尺度舱段水下爆炸试验，验证本文计算方法的有效性。

1 理论模型

已有研究证明在近距爆炸条件下，把冲击波等效为平面波，以同时作用的加载方式存在明显的不合理性。因此水下爆炸可以认为是球面冲击波作用于船体底部，然后向四周扩展的过程。作为近似，为简化计算，以炸药在船体结构中部正下方的工况为研究对象，见图1，同时引入以下假设。

1)在研究船体舱段刚体运动过程中，假定船体等效为周边没有约束的平板，在此只研究舱段的垂向运动，把船体与流场的流固耦合效应简化为船体的附加质量计算，忽略板背面的空气对板运动的阻力，这样爆炸冲击波只需克服船体自身质量及附加质量的惯性使平板向上运动。

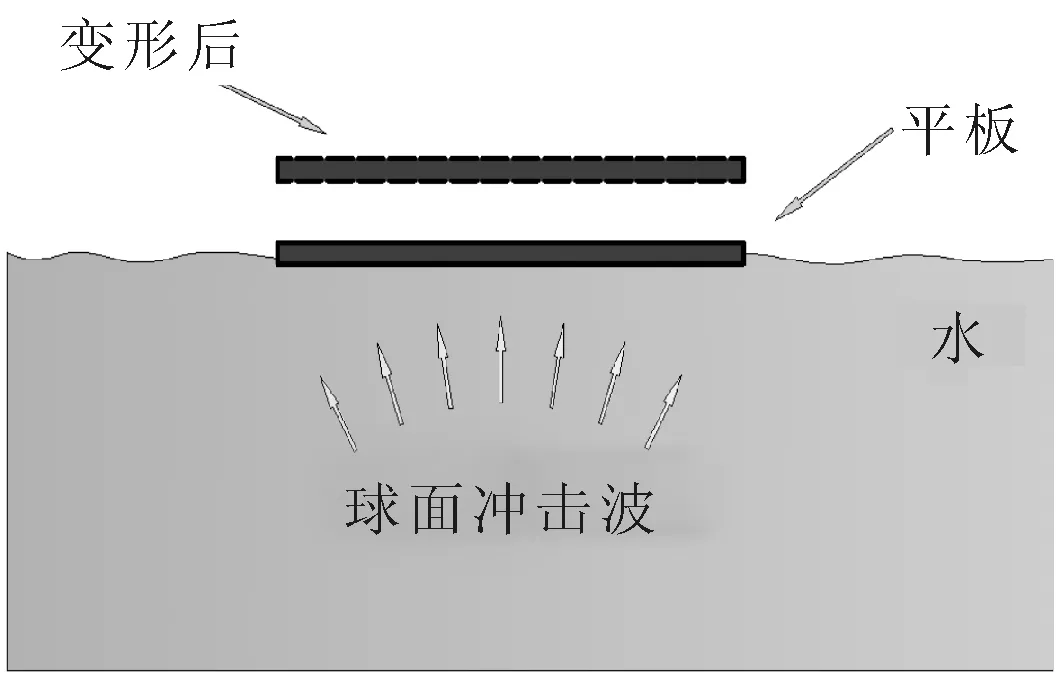
图1 球面冲击波作用于水中平板简化示意

2)在水下爆炸初始的冲击波作用阶段，忽略气泡脉动、射流等载荷对舰船的影响。

3)假定在冲击波作用阶段，运动过程中水和平板不脱离，忽略船体响应过程中重力和浮力变化的影响，图1仅为简化示意图，运动后平板并未脱离水面。

1.1 冲击波压力

药包发生爆炸以后，冲击波以球面波的形式向外传播，由于冲击波从峰值压力衰减到零的时间很短，可以把冲击波等效为以一定厚度沿径向传播的压力水层。如图2所示，其厚度Δr由冲击波在水中传播的速度c及衰减时间ta确定，即

Δr=c·ta

(1)

图2 球面冲击波作用于平板受力示意

当压力水层到达平板中心时，位于正中心的A点首先受到冲击波的作用发生动力响应。冲击压力为

(2)

式中:P(xA,yA,t)——时间t时坐标为(xA,yA)A点处的冲击波压力;

Pm(xA,yA)——坐标(xA,yA)处的峰值压力;

θ——衰减时间常数。

由实测波形数据归纳成经验公式为

(3)

式中:K、α为爆炸类型相关常数，不同资料中给出的数值不同，在此根据具体分析的问题，取K=0.1、α=-0.24[6]。

当冲击波继续传播，到达图中B点时，平板B点处开始受到冲击波压力作用，相对于A点，B点作用时间有一定的延迟，延迟时间td为

(4)

计算时由于对称性，把坐标原点取在平板中心处，此时R可以表示为

(5)

平板各个位置的延迟时间便能计算出。取平板中心A点开始受到平面冲击波作用时记为初始时刻，对于B点，在延迟时间到达之前都未受到任何冲击力的作用，在此定义一个随位置、时间变化的辅助δ(x,y,t)函数

(6)

此时B点的受到球面冲击波的压力便可表示为

(7)

这样，整个平板受到的冲击波压力随时间的变化为

(8)

式中：a，b——平板的长度和宽度。

联立方程(3)～(8)，采用逐步积分方法，对方程(8)进行求解，由于球面冲击波及平板的对称特性，为简化计算，方程可表示为

(9)

1.2 附加质量

由动量定理，平板受到的力Pt(t)与自身垂向速度的关系为

(10)

式中：m——平板自身质量;

ma——平板与流场相互耦合产生的垂向附加质量。

对本文舰船舱段模型附加质量的求解有以下3种方法。

1.2.1 双面浸水矩形板附加质量计算

对于形状规则的矩形平板，其双面浸水的附加质量计算公式[7]为

(11)

式中:a,b——矩形平板的长、宽；

ρf——平板周围流体的密度。

若利用此方法计算船体舱段单面浸水情况，其计算结果的一半可认为是矩形板单面浸水的附加质量。

1.2.2 单面浸水矩形板附加质量计算

船体在水面上爆炸冲击的附加质量问题可以简化为板单面浸水附加质量的计算[8]

(12)

式中：m、n——沿长边和沿短边的半波数，对于板刚体运动，在对附加质量进行粗略估算时可都取为1。

将等效后矩形平板各尺寸代入后可直接计算出单面浸水的附加质量。

1.2.3 边界元法舰船舱段附加质量计算

为得到舰船在水下爆炸冲击环境中较准确的刚体运动响应，在计算附加质量时，不采用理论分析中平板模型的附加质量，而是直接计算船体实际模型的附加质量，ma可以应用流固耦合动力学理论进行求解[9]。在此认为流体不可压缩，不考虑粘性的影响，因此有速度势φ，其梯度为流体速度v=φ。流场域内任意一点的解可以根据边界上已知的速度势φ(狄利克雷边界条件)或者法向速度∂φ/∂n(诺埃曼边界条件)求得。根据Green公式，流场内任意一点的速度势可以用边界S上的速度势及其法向导数表示，或者说，在边界上布置分布源和沿法线方向布置分布偶极便可描述流场域内的函数，利用边界条件，则边界积分方程可以写成

(13)

式中:S——所有边界面;

p,q——边界上的固定点和积分点;

G(p,q)——二维无线水深格林函数;

λ——在p点观察流场的立体角，求解方程为

(14)

求得速度势φ以后，船体的附加质量可通过式(15)求得

(15)

3种方法计算舰船舱段附加质量结果见表1。

表1 附加质量的不同计算方法比较

由表1可见，用矩形板单面浸水方法和边界元法得到的结果最为相近，因此在进行粗略估算时，舰船的附加质量可以利用单面浸水方法求解，要得到较精确理论值时可利用边界元方法进行具体求解。

至此，模型受到的压力及流固耦合作用产生的附加质量都可求出，由式(10)，则冲击波作用下平板运动速度随时间的变化可以表示为

(16)

2 理论模型的试验验证

2.1 舰船实尺度舱段试验验证

为了验证本文所建立理论计算方法的合理性，对某船一舱段进行水下爆炸试验。舰船舱段试验模型长9.1 m，宽7.5 m，高3.85 m，排水量为66 t。具体结构及尺寸见图3。

图3 舱段模型结构尺寸示意

选用TNT炸药，所有工况的药包都近似置于舱段模型的中部正下方爆炸，见图4。试验水池深20 m，具体工况见表2。试验过程中利用高速摄像技术，拍摄舱段在水下爆炸试验过程的运动响应。由于舱段在x方向质量有变化，在试验过程中舱段会沿重心发生轻微的旋转，现阶段只是对舱段的垂向运动进行分析，只测量重心处的垂向运动位移。选取舱段重心所在处的一个试验点，再选择画面中地面上不动的点为参考点，记录试验之前参考点和试验点之间的距离，测量试验后参考点与试验点之间的距离，则两者之差即认为是舱段重心的垂向位移。如此循环往复，就可以测量出舱段重心在爆炸过程中位移随时间的变化，对位移时历曲线微分便可得到舱段在此过程的运动速度随时间的变化。

图4 试验工况示意

表2 试验工况表

工况药量/kg爆点距离/m冲击系数183.210.88284.420.64385.900.48

由于实际试验过程，模型上下浮动，浮力和重力的变化会对模型的速度产生影响，实际测出的速度变化规律性较差，但在冲击波作用阶段总有一个速度峰值，此峰值理论上应为分析模型中冲击作用结束后平板的速度。下面以工况1为例给出冲击波压力、平板受到冲击波的压力变化及理想情况下(不考虑重力、浮力和气泡等其它载荷的影响)平板刚性运动速度随时间的变化曲线，见图5～7。

图5 冲击波压力随时间变化曲线

图6 平板受到冲击波压力随时间变化曲线

图7 平板刚性运动速度随时间的变化曲线

由图5可见，在药包爆炸后，冲击波压力迅速达到峰值，很快又出现衰减，在4 ms左右已经趋近于零。相对于冲击压力，如图6，平板受力一开始出现一个渐进过程，不是迅速达到峰值，而是在1.1 ms左右达到最大值，之后在3.5 ms左右受到的冲击波压力衰减为零。平板运动速度则一直呈增加趋势，如图7所示，因水下爆炸冲击波阶段作用时间极短，舱段在冲击波作用下的位移响应相对于吃水数值较小，因此理论分析中没有考虑重力及浮力对模型的影响，所以在平板受冲击压力最大时刻，其加速度最大，在受力趋于零时，平板达到最大速度，之后由于重力、气泡脉动载荷等，船体速度肯定还会发生变化，而本文并未考虑冲击波作用之后的船体响应阶段。

根据不同工况测得试验模型的速度，对理论值进行验证，见表3。

表3 不同工况舱段最大速度试验值与理论值对比

从理论预报的误差可以看出，随冲击因子的增大，即爆距的减小，误差越来越大，但控制在15%之内。图8更能显示出试验值和理论值随爆距变化的差异。

本文并未利用能量法，而是直接计算船体受力，利用动量定理计算的船体刚体运动，由于在此并未考虑冲击波反射透射等影响，可能导致船体受力的理论计算值比实际偏小，所以整体上试验值都比理论计算值偏大。随爆距减小，误差增大可能是药包离船体太近，气泡的存在，对模型速度产生较大影响。同时爆距较近时，舱段发生了一定程度的旋转，增大了试验测量垂向位移的误差，从而致使试验值大于理论计算值。在爆距较远的工况3时，相对误差只有2%，可见本文理论模型可以较准确地预报船体刚体运动的速度。

2.2 船体梁模型试验验证

为使理论模型具有普遍适应性，不只局限于试验模型的计算，由文献[5]中钢制船体梁模型的试验数据，利用其中工况1(药量9 g，爆距0.5 m)的船体梁刚性运动状态中点位移的曲线，见图9。对曲线进行微分可得到中点的速度，梁上冲击波作用时间约为0.83 ms。

图9 船体梁中点刚体运动位移试验值

从图9中看出，在0.8 ms之前出现A、B两个曲线斜率较大时刻。B区域可能开始受到气泡脉动的影响，模型速度开始变大。在此之前，速度峰值出现在曲线斜率较大的A区，对此区域进行微分求导，得出速度的试验值，其与理论值的比较见表4。

表4 船体梁中点最大速度试验值与理论值对比

在此工况下，冲击因子较小，模型完全为刚体运动过程，应用本文方法很好地预报了模型刚体运动的速度，从而进一步证明了本文理论的正确性。

3 结论

1)舰船舱段总体并不是在冲击波压力达到峰值的时候受到最大的冲击压力，而是在一定的时间延迟后，达到冲击波作用阶段最大的加速度运动过程。

2)在爆距较近的水下爆炸环境中，舰船舱段发生一定程度的旋转，增大了试验测量垂向位移的误差;未考虑冲击波在船体表面的反射透射等的影响，应用本文理论进行预报会比试验值偏小。

3)冲击因子较小工况下，根据船体梁模型试验结果，模型基本处于刚体运动状态时，本文方法可以得到水下爆炸冲击波作用下比较准确的速度预报。

[1] ZHANG Aman, ZHOU Weixing,WANG Shiping,et al.Dynamic response of the non-contact underwater explosions on naval equipment[J].Marine Structures,2011,24(4)：396-411.

[2] JEN C Y,LAI W H.Transient response of multiple intersecting spheres of deep-submerged pressure hull subjected to underwater explosion[J].Theoretical and Applied Fracture Mechanics,2007,48(2)：112-126.

[3] CHIRICA Ionel,BOAZU Doina,BEZNEA Elena-Felicia.Response of ship hull laminated plates to close proximity blast loads[J].Computational Materials Science,2012,52(1)：197-203.

[4] 李海涛，朱 锡，张振华.水下爆炸球面冲击波作用下船体梁的刚塑性动响应特性[J].工程力学，2010，27(10)：202-207.

[5] ZHANG N,ZONG Z.The effect of rigid-body motions on the whipping response of a ship hull subjected to an underwater bubble[J].Journal of Fluids and Structures,2011,27：1326-1336.

[6] 恽寿榕，赵衡阳.爆炸力学[M].北京：国防工业出版社，2005.

[7] SINHA J K.Added mass and damping of submerged perforated plates[J].Journal of Sound and Vibration,2003,260：549-564.

[8] 吴 芳.板和加筋板附加水质量算法研究[D].大连：大连理工大学，2006.

[9] 张阿漫，戴绍仕.流固耦合动力学[M].北京：国防工业出版社，2011.