采用比例谐振控制的三相4桥臂并网逆变器的研究

董钺，芮春保，李钊，刘江华，邱晗

（1.天津电气传动设计研究所有限公司，天津 300180；2.江苏辉伦太阳能科技有限公司，江苏 南京 210061）

1 引言

对于接入380 V电网、且带有储能单元（通常为蓄电池）的分布式光伏三相并网逆变器，首先要保证本地三相4线负载供电，特定情况下也要向电网输出功率，可以采用如下运行模式：

1）当光伏电池功率超过本地负载功率时，将多余的能量储存在蓄电池内，在蓄电池充电完成后，维持浮充状态，将剩余能量输送至电网；

2）当负载功率超过光伏电池功率时，由光伏电池和蓄电池共同为本地负载供电；光伏电池没电时完全由蓄电池供电，蓄电池没电时完全由光伏电池供电，二者互补，不足部分由电网补充；

3）当负载功率超过逆变器容量时（某一相、两相或三相），由光伏逆变器和电网共同承担负载电流。

由于生活负载中单相负载较多，通常为三相4线形式（如考虑地线，则为三相5线制），因此负载电流中除正、负序分量外还有零序分量。为保证零序电流通路灵活可控，并网逆变器既可采用三单相H桥结构，也可采用三相4桥臂拓扑结构。与前者相比，后者具备如下优势：

1）电力电子器件由12个减少为8个；

2）对于交流侧无变压器的逆变器，三单相H桥结构需要3个隔离的直流母线，而4桥臂结构只需要一个直流母线；

3）对于三单相H桥结构，为减小直流母线倍频电压波动，需要电容量较大；而三相4桥臂结构，在单相输出的情况下，输出容量为总容量的1/3，可减少直流滤波电容总量。

因此，本文中的并网逆变器采用三相4桥臂结构［1-5］。带有储能单元的光伏逆变器拓扑结构如图1所示。

图1 储能光伏逆变器拓扑结构Fig.1 Structure of energy storage PV inverter

在图1所示结构中，光伏电池所接Boost斩波电路进行最大功率跟踪；蓄电池通过控制双向斩波电路输出到DC Link1的电流，根据自身充放电曲线，平衡直流输入与交流输出之间的功率；DC/DC隔离变换器起隔离作用；逆变器对本地负载电流进行跟踪。

对于并网逆变器，直接控制对象为并网电流。为保证其动、稳态性能，既可采用矢量控制、也可采用比例谐振控制对并网电流进行调节。采用矢量控制，需要根据电网电压，对电流进行旋转坐标变换及前馈电流解耦［6］；采用比例谐振控制，可以直接对正弦电流进行无静差调节。本文采用比例谐振电流控制，并以负载电流作为逆变器并网电流给定，可以在容量范围内对负载电流进行跟踪。最后，通过试验，验证了该方法的可行性。

2 并网电流比例谐振控制器的设计

2.1 比例谐振控制器

在控制系统中常用的比例积分（PI）控制器，可以对直流信号进行稳态无静差跟踪。若要对工频交流量进行稳态无静差控制，通常采用矢量控制，通过旋转坐标变换，将交流量变换为直流量，经PI控制器后，再将控制器输出经旋转坐标反变换，还原为交流量。比例谐振控制的本质即为将PI控制与坐标变换结合在一起，对交流量进行无静差控制，其谐振部分传递函数如下式所示：

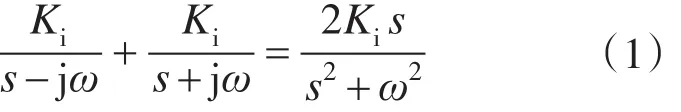
式中：Ki为谐振系数；ω为谐振角频率，ω=2πf。

由式（1）可知，谐振传递函数即为在角频率为±ω时的广义积分器，可以实现对任意频率的正弦交流量进行无差跟踪。

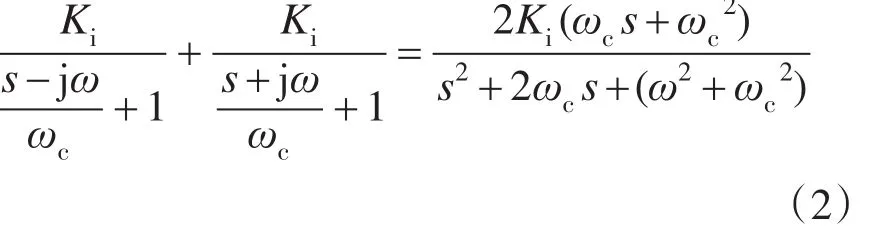
由于在通常情况下ωc取 5～15［7］，而对于工频，ω=100π，因此分母可近似表示为

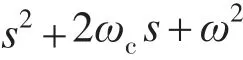
此外，为保证其带通特性，分子常数项亦可去掉，故谐振环节传递函数可简化为

2.2 电流环传递函数

由于采用比例谐振电流控制，因此，电流环给定为正弦量。为尽量减小保证逆变器输出电流中的高频谐波分量，逆变器输出端采用LCL滤波，逆变器交流侧数学模型如图2所示。

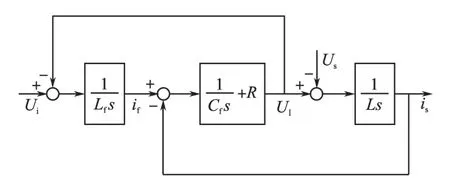
图2 逆变器交流侧数学模型Fig.2 Mathematic model of inverter AC side

图2中，Lf为滤波电感，Cf为滤波电容，R为阻尼电阻，L为并网电感，Ui为逆变器交流输出电压，if为逆变器输出电流，UI为滤波电容支路电压，Us为电网电压，is为逆变器并网电流。

逆变器交直流之间的数学关系如下式所示：

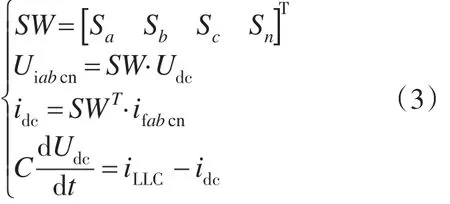
式中：SW为逆变器开关函数；Udc为逆变器直流电压；idc为逆变器直流电流；iLLC为DC/DC隔离变换器（LLC）输出电流。

由式（3）可知，逆变器交流输出电压Ui为开关函数与直流电压乘积，通常情况下，为尽量消除直流电压波动对交流电流的影响，将电流调节器输出乘以1/Udc，可使逆变电流与直流电压解耦，消除二者之间的非线性。

此外，为加快电网电压波动时的电流响应速度，同时减轻电网电压畸变引起的并网电流的低次谐波，在电流控制器输出端引入电网电压前馈。由图2可知，采用该措施可使逆变电流与电网电压解耦。加入比例谐振控制器后的传递函数如图3所示。

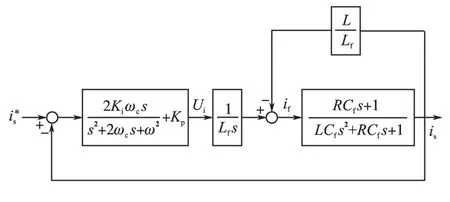
图3 电流闭环传递函数Fig.3 Transfer function of inverter current loop

2.3 负载电流跟踪

本文中的逆变器，输出端除并入电网外，还接入本地负载，结构如图4所示。

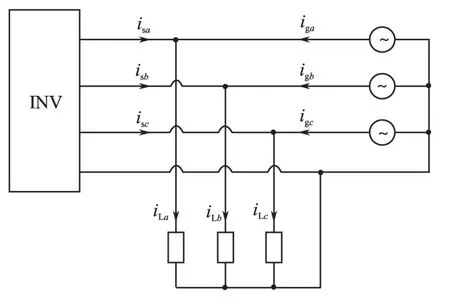
图4 逆变器输出结构图Fig.4 Output structure of inverter

图4中，iga，igb，igc为入网电流，iLa，iLb，iLc为本地负载电流。如图4所示方向，逆变器并网电流与入网电流代数和即为本地负载电流，此电流即可作为逆变器并网电流的给定，实现对负载电流的跟踪。

4桥臂逆变器有3个控制自由度，第4桥臂只对零序电流进行调节，而零线电流为三相线电流之和，因此，第4桥臂控制信号取前3桥臂调节器输出信号代数和的负值，即前3桥臂对正负序电流分量进行控制，而第4桥臂与前3桥臂一起对零序电流进行控制。

此外，为提高直流电压利用率（使载波调制方式等同于空间矢量调制方式），三相线及零线同时叠加交流偏置信号［6，8］。4桥臂控制信号结构如图5所示。

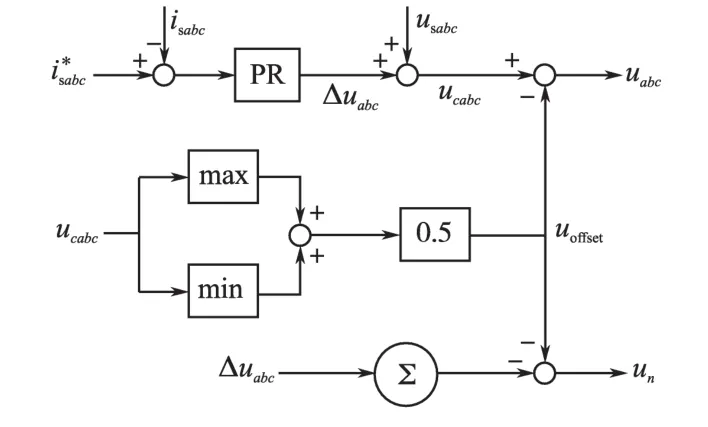
图5 逆变器4桥臂控制结构Fig.5 Control structure of inverter four legs

3 实验波形

逆变器相关参数为额定电压400 V，额定频率50 Hz，额定容量7.2 kV·A，光伏电池额定功率6 kW，蓄电池额定电压192 V，蓄电池容量50 Ah。

图6、图7为实验波形（示波器2.95 A/V）。

由实验波形可见，采用本文所述控制方法，可使逆变器并网电流对负载电流进行稳态无静差跟踪。

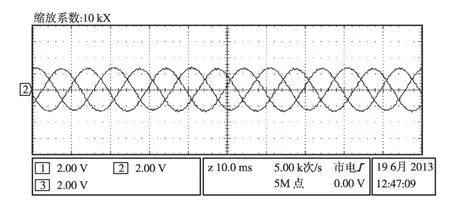
图6 三相对称逆变电流波形（输出为66%额定功率）Fig.6 3⁃phase symmetrical current waveforms of inverter（66%rated power output）

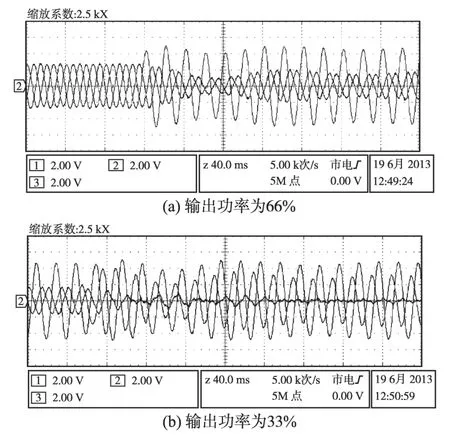
图7 由三相对称输出切换至单相满功率逆变电流波形Fig.7 Current waveforms of inverter when 3⁃phase symmetrical switch to 1⁃phase rated power

4 结论

为适应三相4线负载，本文对4桥臂逆变器并网电流比例谐振控制方法进行了分析与建模，将负载电流作为逆变器并网电流给定，在逆变器容量范围内可实现对负载电流的跟踪。通过实验波形验证了该控制方法的有效性与可行性。

［1］王晓刚，谢运祥，黄少辉，等.四桥臂逆变器SPWM和SVP⁃WM的归一化研究［J］.电机与控制学报，2010，4（1）：23-28.

［2］陈玲，张兴，杨淑英，等.带不平衡负载的三相四桥臂逆变器的研究［J］.合肥工业大学学报：自然科学版，2009，32（4）：486-490.

［3］杨宏，阮新波，严仰光.采用SVM控制的四桥臂三相逆变器［J］.电气传动，2003，33（2）：32-34.

［4］刘秀翀，张化光，陈宏志.四桥臂逆变器中第四桥臂的控制策略［J］.中国电机工程学报，2007，27（33）：87-92.

［5］孙驰，毕增军，魏光辉.基于空间矢量电流调节器的三相四桥臂逆变器的解耦控制研究［J］.电工电能新技术，2003，22（3）：37-40.

［6］马小亮.高性能变频调速及其典型控制系统［M］.北京：机械工业出版社，2010.

［7］Teodorescu R，Blaabjerg F，Liserre M，et al.Proportional Resonant Controllers and Filters for Grid⁃connected Voltage Source Converters［J］.The Institution of Engineering and Technology 2006，IEE Proceedings Online No.2006：8.

［8］周卫平，吴正国，唐劲松，等.SVPWM的等效算法及SVP⁃WM与SPWM的本质联系［J］.中国电机工程学报，2006，26（2）：133-137.