一种基于交流伺服系统的非线性控制方法

周博，徐大林，张允志

（江苏自动化研究所，江苏 连云港 222006）

1 引言

随着半导体技术、永磁材料、电力电子技术、控制理论和计算机技术的飞速发展，交流伺服控制系统在工农业中的应用越来越广泛，随着工业技术的不断提高，对伺服系统的控制性能也提出了更高的要求，不仅要求稳态精度高，超调小，而且对于系统的响应速度和鲁棒性也提出了更高的要求。由于交流伺服系统是典型的非线性系统，因此采用传统的线性控制方法很难取得很好的控制效果。针对这些问题，近些年来，大量的学者进行了研究，提出了多种方法在伺服系统中的应用。主要有自适应控制［1-2］，自适应控制主要分为模型参考自适应和自校正控制，需要在线辨识系统参数，运算繁琐，计算量较大。滑膜变结构控制［3-4］，这种控制方法与系统参数及扰动无关，鲁棒性较强，但是存在比较强的抖震问题，因而限制了它的应用。智能控制，主要有模糊控制［5-7］和神经网络控制［8-9］，在实际应用中，一般将智能控制方法和其他的一些方法结合使用，以达到好的控制效果，因此加大了算法的复杂度和计算量。针对这些问题，本文在对交流伺服系统控制规律分析的基础上提出了一种非线性控制方法，确定控制量非线性变化趋势，根据实时误差和误差变化自整定非线性参数，调整控制量变化快慢以提高系统的鲁棒性和快速性。同时提出了控制量增量因子自调整法以改善系统的动态过程。最后在1台48 V/2.3 kW永磁交流伺服驱动器上对本文提出的算法进行验证，实验结果表明，与传统线性控制方法相比，文中提出的非线性方法大大提高了控制系统的响应速度和驱动器的调速范围，增强了系统的鲁棒性。

2 非线性控制原理

在伺服控制系统中，系统的响应与控制量的大小和变化有着直接的联系，响应速率和控制量大小成正比，控制量发生震荡往往会造成系统的震荡，在系统误差较小时控制量的大小一般和系统超调成正比。因此，在控制过程中想要取得好的性能，调整控制量的大小和变化非常重要。对于高性能的伺服控制系统，针对快速响应的要求，控制量初始值选取为一个较大的值。为了避免偏差的累加作用对控制系统造成的影响，控制算法采用增量式方法，如下式：

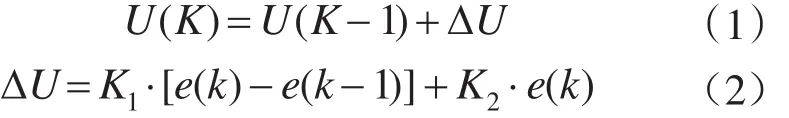
式中：U(K)，e(K)分别为系统控制量和误差；K1，K2分别为非线性参数，K1为误差变化权重，主要影响系统响应的动态过程；K2为误差变化权重，主要影响系统稳态过程。

通过对控制量变化趋势的分析，确定非线性参数变化规律，构造非线性函数。

2.1 误差变化权值非线性整定原理

在系统响应的上升过程中，误差变化为负值，因此误差变化权值大小反应了控制量减小得快慢，权值取得过大，使控制量变得太小，响应过程缓慢；权值太小，使控制量过大，造成超调。因此要根据实时误差和系统响应速度综合调整权值大小，其中响应速度可以用误差的变化来反应。权值K1的变化趋势主要可以分为以下5个状态见表1，其中dete为误差变化。

表1 K1变化趋势分析表Tab.1 Trend analysis table ofK1

根据以上分析，构造误差变化权值增量自整定非线性函数如下式：

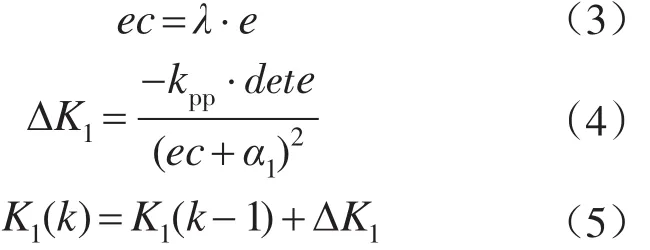
式（3）中，λ是误差比例因子，一般取一个较小的值，误差比例因子是将系统误差进行归一化处理，根据实验中使用的电机额定转速2000 r/min归一化到3，因此这里我们取误差比例因子为0.0015。α1因子的设定是使系统在发生超调时误差变化权值仍能够快速增大以使控制量快速减小从而抑制超调，一般取一个较小的值，在这里取归一化整数的1/10，取0.3。kpp为误差变化权值增量系数，起到综合调整比例增量大小的作用。增大kpp可以减小超调，但是会使响应变慢，减小kpp可以加快系统响应速度，但是过小会产生超调，因此在实际中要综合考虑系统的动稳态过程，进而对增量系数进行调整。

2.2 误差权值非线性整定原理

误差权值K2主要影响系统的稳态过程，在响应初始阶段系统误差取较大的正值，由于初始控制量设置为较大的值，因此误差权值应取小值，以避免控制量增加的过大而使系统产生超调甚至震荡，随着误差的减小，权值应快速增大，以减小系统稳态误差，加快系统响应末态时的响应速度。构造误差权值增量自整定非线性函数如下式：

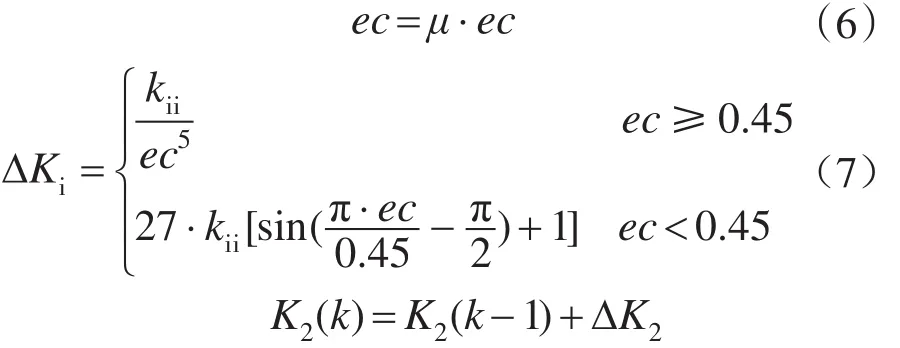
式（6）中，μ为误差权值非线性函数增量系数，通过增大或减小此系数，可以调整非线性曲线的伸展大小从而影响积分因子的变化进而调整系统的响应过程。减小μ，可以加快误差权值的增加速度，从而加快系统的响应过程，但是误差权值增加的过大特别是在响应的初始阶段增加的过快会造成控制量过大而使系统最终产生超调。kii为误差权值增量系数，在实际中的作用和μ类似。它主要是综合调整系统初始和末态过程中权值变化快慢，而误差权值非线性函数增量系数μ主要是调整初始时刻权值的变化过程，在非线性函数增量系数的调试过程中，初始可以取一个稍大的整数，试验中取作2，然后根据系统响应快慢和超调对参数进行上下调整，如果系统产生超调，可以以0.1为一个单位适当增加增量系数，如果没有产生超调但系统上升时间较长，可适当减小增量系数直到系统达到一个较好的性能。

3 控制量增量因子自调整算法

在伺服控制中，随着系统误差的逐渐减小，误差权值快速增大，可能造成控制量发生震荡进而使系统响应出现震荡，随着系统越接近稳态，发生震荡的可能性越大，因此，针对这种现象，提出了控制量增量因子自调整法来改善系统响应。在系统响应的上升阶段，误差变大，说明系统出现震荡，应对控制增量做相应的调整，调整算法如下式：

其中

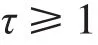
通过调整式（10）的增量因子τ可以改善系统的动态响应过程，抑制震荡。增大τ，可加快响应速度，减小震荡，但取得过大会造成系统产生更大的震荡和超调，较小τ取不到调整的作用，因此在实际调整中需要综合考虑系统动态响应对增量因子进行调整。根据调试经验，增量因子调整过程中，初始设定为1，然后根据实际动态过程以0.1为一个单位适当增加，直至达到比较理想的效果。

4 实际验证

针对以上提出的非线性算法，在1台48 V/2.3 kW伺服驱动器上进行实际对比验证，主控芯片选用TI公司的TMS320F2812，功率驱动部分选用三菱公司的PM75RLA120型号IPM，分别使用传统线性PI控制和本文提出的非线性方法，在设定转速为2000 r/min时分别调整一组较好的参数，对系统响应进行对比分析。参数不变，分别测试电机在低速500 r/min和中高速1000 r/min时两种方法的性能，进行对比分析。最后将使用控制量增量因子自调整法和没有使用此方法时系统的控制性能进行对比分析。非线性参数和线性PI参数见表2。系统响应如图1～图4所示。

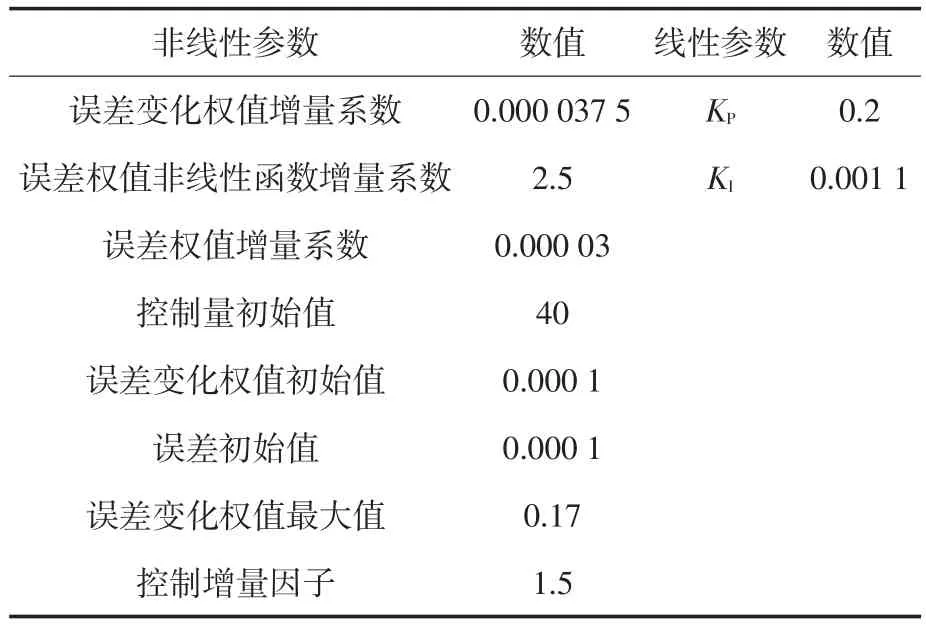
表2 控制器参数Tab.2 Controller parameters

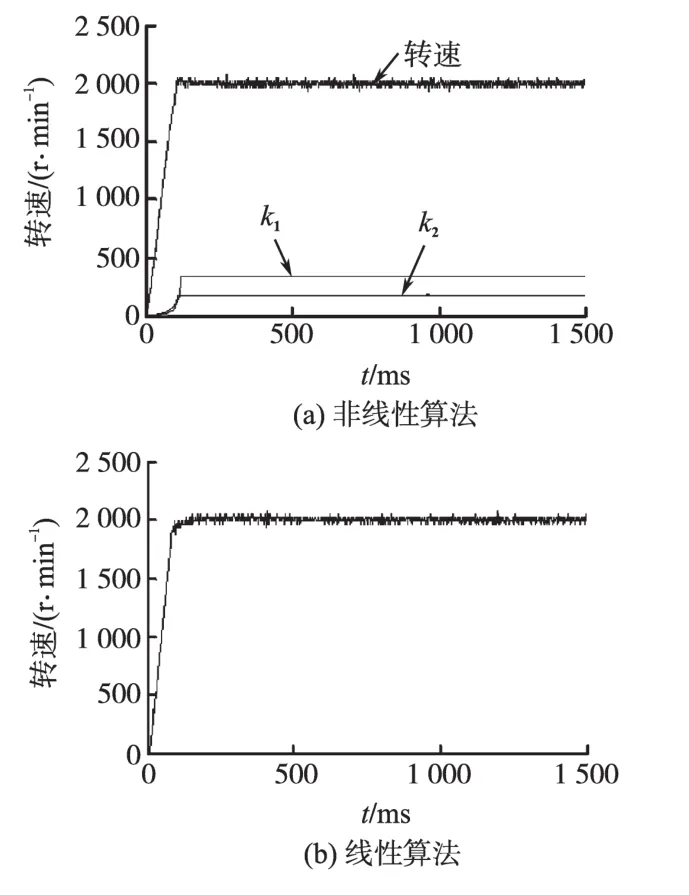
图1 2000 r/min时系统响应Fig.1 System response in 2000 r/min

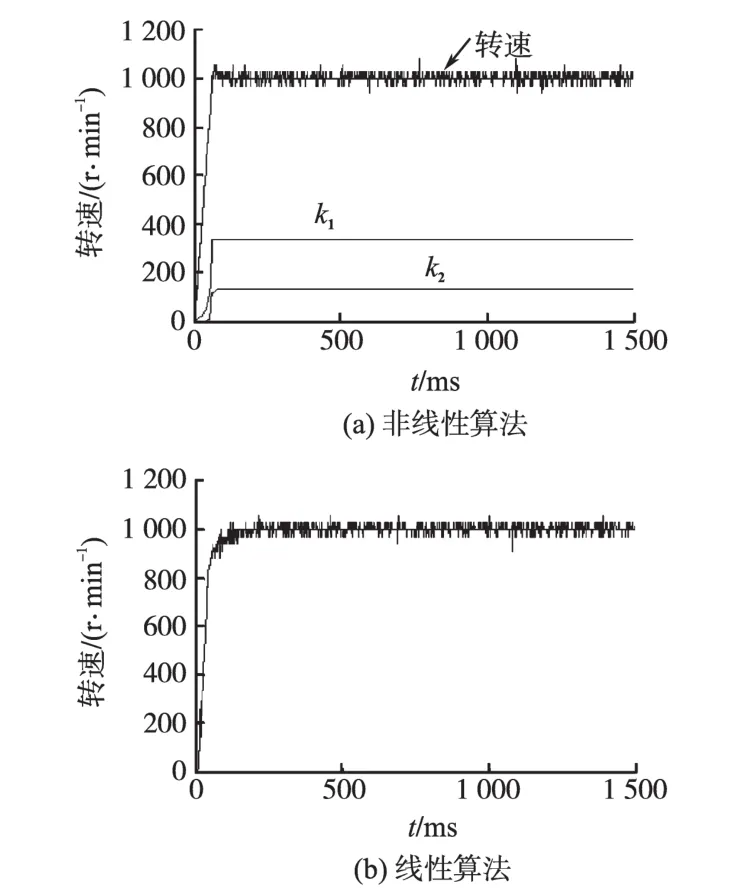
图2 1000 r/min时系统响应Fig.2 System response in 1000 r/min

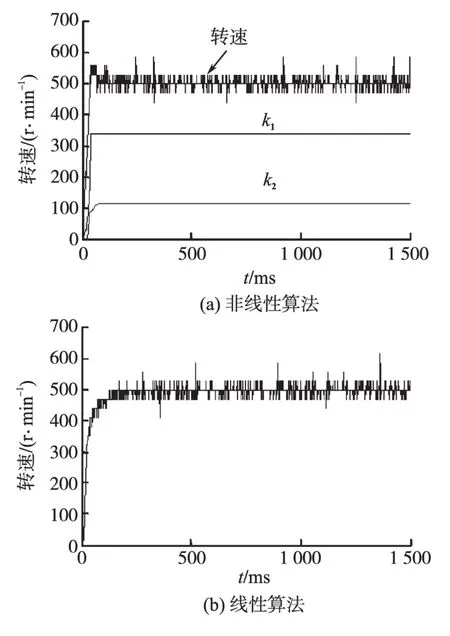
图3 500 r/min时系统响应Fig.3 System response in 500 r/min

图4 2000 r/min无自调整非线性算法系统响应Fig.4 No self⁃tuning nonlinear systemresponse in 2000 r/min

稳态响应时间如表3所示。

表3 稳态响应时间Tab.3 Steady⁃state response time

实验中控制系统转速环采样周期设定为0.5 ms，编码器为12圈12位，转速采集的最高精度为30 r/min，因此在系统稳定后响应曲线会出现上下大小为30 r/min左右的波动，这是由于编码器采集的问题，实际电机此时已经稳定运行。响应曲线中显示的误差和误差变化权值k2，k1是经过一定比例放大后的结果。

由表3和图1～图3可以看出，本文提出的非线性算法大大提高了系统的响应速度，调速范围更大。由图2b可以看出在接近给定转速时，系统有震荡的现象，但是使用文中提出算法的控制系统响应曲线没有出现这种情况。图4是没有使用控制量增量因子自调整方法的系统响应曲线，与有自调整的图1a响应曲线相比，前者响应的动态过程明显有波动现象，而后者动态响应十分平滑。

5 结论

对于交流伺服系统高性能控制，针对传统线性控制算法存在的种种不足，从交流伺服系统控制规律出发，提出了一种计算量小的非线性控制算法并且阐述了算法的原理。并且通过在1台48 V/2.3 kW伺服驱动器上的实验证明了文中提出算法的有效性。

［1］钟义长，钟伦珑.永磁同步电动机双闭环参数辨识自适应控制［J］.微特电机，2012，40（4）：47-50.

［2］徐小增，秦忆.矢量控制异步电动机的自适应控制和参数辨识［J］.电机与控制学报，2002，6（2）：111-114.

［3］Xiao Guangzhang，Li Zhisun，Ke Zhao，et al.Nonlinear Speed Control for PMSM System Using Sliding⁃mode Control and Disturbance Compensation Techniques［J］.IEEE Transac⁃tions on Power Electronics，2013，28（3）：1358-1365.

［4］刘颖，周波，方斯琛.基于新型扰动观测器的永磁同步电机滑模控制［J］.中国电机工程学报，2010，30（9）：80-85.

［5］汪利峰，王耀南，陈正龙.基于预测模糊PI的异步电机控制［J］.电气传动，2009，39（2）：52-55.

［6］Cheng K，Tzou Y.Fuzzy Otimization Techniques Applied to the Design of a Digital PMSM Servo Drive［J］.IEEE Trans⁃actions on Power Electronics，2004，19（4）：1085-1099.

［7］SHI Huali，HAOgu.Fuzzy Adaptive Internal Model Control Schemes for PMSM Speed ⁃regulation System［J］.IEEE Transactions on Industrial Informatics，2012，8（4）：767-779.

［8］刘贤兴，胡育文.永磁同步电机的神经网络逆动态解耦控制［J］.中国电机工程学报，2007，27（27）：72-76.

［9］王群京，殷伟，姜卫东，等.基于神经网络预测控制的PMSM伺服系统的仿真研究［J］.电气传动，2008，38（10）：54-57.