独立光伏系统中浮充控制的模型分析与应用

冯仁剑，赵帅，卢晓东

（北京航空航天大学仪器科学与光电工程学院，北京 100191）

1 引言

如今铅酸蓄电池广泛应用于独立光伏系统中，作为发电系统的关键支撑环节，对其合理地充电控制对于系统的高效可靠运行至关重要。独立光伏发电系统中，蓄电池的浮充控制不仅能够实现对蓄电池最大容量的充电，同时可有效避免阀控铅酸蓄电池饱和状态下析气现象的发生［1］。但是独立光伏系统对蓄电池的浮充充电要求十分严格，如果浮充电压过高，容易引起蓄电池发生热失控和失水现象，严重影响电池的使用寿命；相反，若浮充电压过低，浮充电流将呈指数形式下降，降低蓄电池的使用效率，研究显示［2］，5%的浮充电压偏差会造成约30%的蓄电池电量损失。

因此，本文针对独立光伏发电系统浮充电阶段的电压控制展开研究，对浮充状态下充电控制器关键环节进行精确模型分析，并设计一种高效蓄电池浮充控制器，在充电方式上保证蓄电池的有效使用寿命，从而实现独立光伏发电系统的高效稳定运行。

2 浮充系统模型分析与设计

在充电过程中，蓄电池容易受到外界条件的干扰，使其端电压产生一定范围的波动，从而影响蓄电池的正常充电，导致光伏系统储能环节的提前失效［3］。其中光照强度具有瞬时变化性，对蓄电池充电电压的影响尤为明显，本文使用了设计结构如图1所示的控制系统，以脉冲调制信号（PWM技术）的占空比Duty为控制量，以光照强度So作为干扰量，对蓄电池Rb（s）和光电池板Pv（s）进行动态建模分析，最后完成控制器的设计。

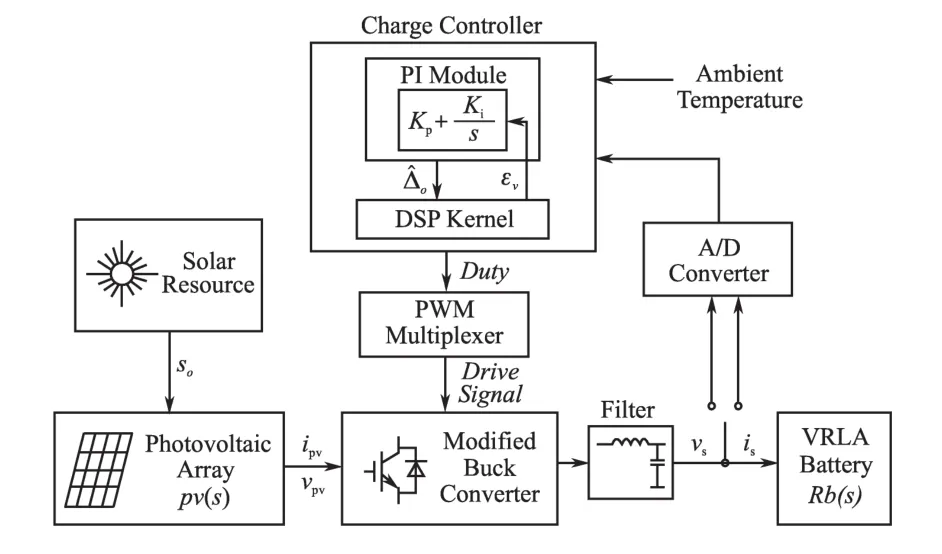
图1 独立光伏发电系统结构Fig.1 Structure of stand⁃alone PV system

2.1 VRLA蓄电池模型的建立

蓄电池作为独立光伏系统基础和关键的环节，对其在充电过程中准确可靠地建立动态模型是基本和首要的任务。精确的蓄电池模型可以使用机理分析法建立起来，也就是通过分析充电时蓄电池内部复杂的电化学反应过程而得到［4］。

本文针对充电系统处于在过充点电压区域内的稳态工作环境，需要相对简易但可靠精确的蓄电池动态模型。因此采用阶跃信号输入测试法［5］：在既定状态下，对阀控蓄电池输入相应不同的阶跃电流信号，与此同时瞬时采集输出端电压信号，这样将蓄电池的复杂额定非线性模型可以转化为稳态下小信号分析模型，即在稳态的过充点电压点附近的扰动模型。

测试实验采用深圳FirstPower公司生产的LFP1238型12V/40AH型铅酸蓄电池。测试实验设定条件如下：蓄电池状态设定在剩余容量SoC为93%，静态工作电压Vb为14 V；前端是由3个恒流电流源提供的不同电流输出构成，通过在一个开关组件控制下组成测试所需的阶跃电流输入，3种电流状态分别是在蓄电池以14 V工作电压时稳态电流为偏置下的0 A，-1 A，+1 A电流浮动值。后端电压值的数据获取是通过隔离分压信号板，并利用USB-4716型研华数据采集卡的DAQ模块并在1 kHz采样频率下来完成。

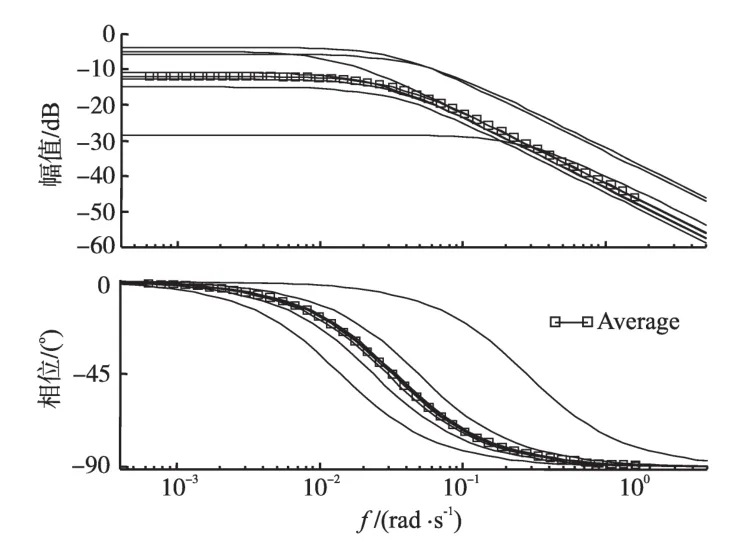
图2 均化蓄电池动态模型波特图Fig.2 Bode plot of the battery dynamics model

将多次测试实验所得测量数据作均化处理，并以此绘制蓄电池动态模型波特图如图2所示。由此可以看出在该静态工作状态下，蓄电池表现出的输入特性接近于一阶线性环节，故按照一阶系统的数学模型可以较为准确地描述浮充状态下阀控蓄电池的动态特性。推导出的平均数学模型为

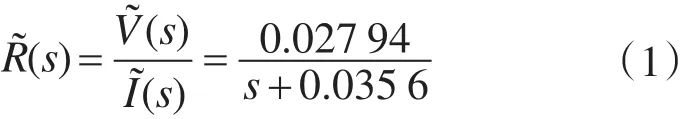
2.2 Buck控制电路建模

Buck电路作为蓄电池充电的直接控制环节，在该系统中具有枢纽作用，作为PWM型DC/DC变换器中较为基本的一种，具有电路简单和优良的输出电压调节控制性能［6］。

图3 改进型Buck电路驱动波形图及阶段电路拓扑结构Fig.3 Driver signal and topology model of the improved Buck circuit in two states

如图3所示，实验方案采用的是改进型的两开关Buck电压调节器，与典型的Buck电路多出一个功率开关管，其中Q2与Q1的导通截止状态始终相反，这种设计的优势是可以大幅减少电路中功率的消耗：Q1导通时，电流流经蓄电池，通过电导太阳能电池对蓄电池进行充电；Q1截止时，L，D，蓄电池形成回路，电路起到续流的作用，此时不必消耗功率在D上，减少整个电路的功耗。由以上分析可以得到图3所示的Buck电路驱动信号状态图。

本文使用状态空间平均法对该两开关Buck型电压调节器进行动态模型分析，以电感电流IL和电容电压UC作为状态方程的状态变量，太阳能电池板提供的电压US作为模型输出。由Buck电路充电导通和续流截止状态在一个开关周期内用时间平均得到有关开关频率的非线性状态方程为

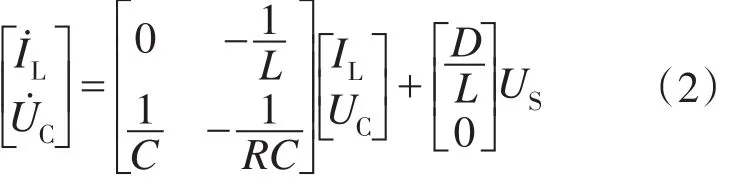
式中：D为PWM驱动信号的占空比。

然后在系统处于浮充状态的工作点下进行小信号模型分析：在式（2）中除了电阻电容和电感是常量，其他皆为变化的信号量。所以对式（2）进行偏差线性化建模，可以得到该非线性系统的扰动模型状态方程如下：

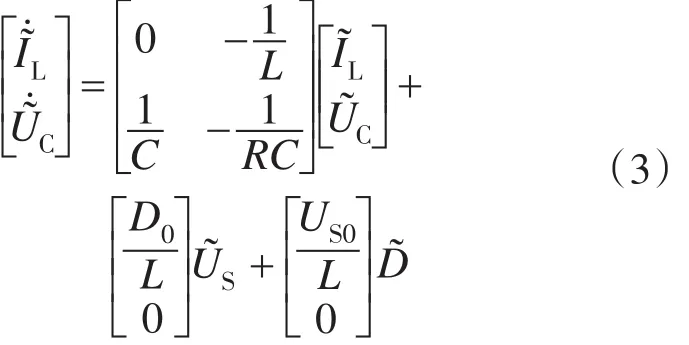
式中：D0和US0分别为在系统设定的工作点时PWM驱动信号的占空比和光电池输出电压值。根据之前的蓄电池结构建模中，以蓄电池的充电扰动电流作I～(s)模型输入，由此选择Buck控制电路的输出电流（即式中的I～L）为中间变量，对式（3）进行拉普拉斯变换后求解可得到其传递函数式如下：

2.3 浮充控制器设计

在多种外界作用因素中，光照强度会在一段时间内根据天气状况发生持续变化，并且随某些极端条件产生剧烈跳变，所以采用光照强度作为光电池模型同时也是充电系统的输入。光电池板的电压Vs在变化的光强输入So下响应迅速，达到了ms级，而相比之下蓄电池输出变化缓慢。因此在稳态的工作电流下，光电池板可以作为零阶系统模型进行分析［2］，并且能够通过简易测试实验中获取其输入输出特性，结果为

在之前对蓄电池的建模分析中，采用的是电流作为蓄电池输入，因此在整体系统模型建立中，以流过蓄电池的电流即电感电流扰动信号和PWM驱动信号占空比扰动值D～作为系统的中间控制变量。充电控制器使用PI算法对驱动信号的占空比D进行调节控制，其中PI控制器模型为

其中在系统模型仿真中，通过分析仿真结果，不断修正Kp和Ti值，从而使得系统控制过程达到理想的快速性和稳定性，并限制超调量范围，以防止过充对蓄电池在充电过程中造成的损害。在光电池、蓄电池和Buck电路模型（参数采用L=220 μH ，C=330 μF ，R=5 Ω，f=5 MHz，与之后实验参数一致）建立的基础上，加入PI比例积分控制模块进行反馈调节，完成整个系统的仿真模型，如图4所示。

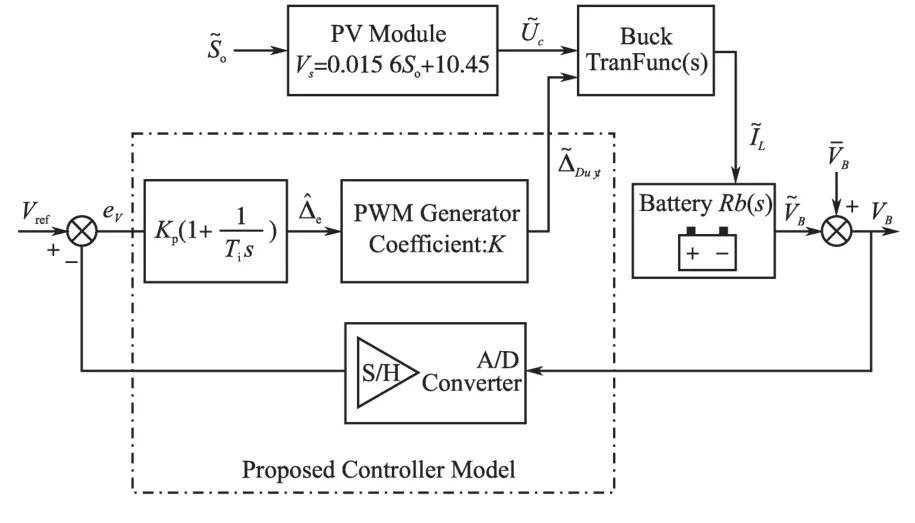
图4 充电系统仿真结构图Fig.4 Simulation diagram of charging system

图5和表1是通过Simulink仿真工具搭建系统模型后的部分仿真结果。

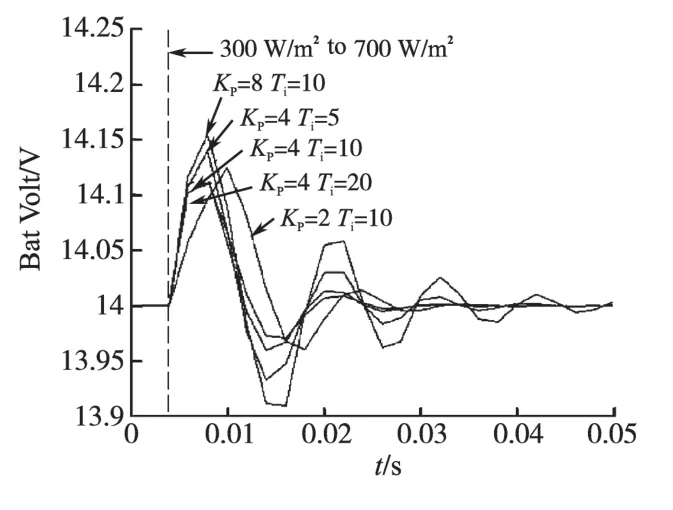
图5 不同参数的PI控制下扰动仿真的部分结果Fig.5 Partial simulations in different parameters of PI feedback control

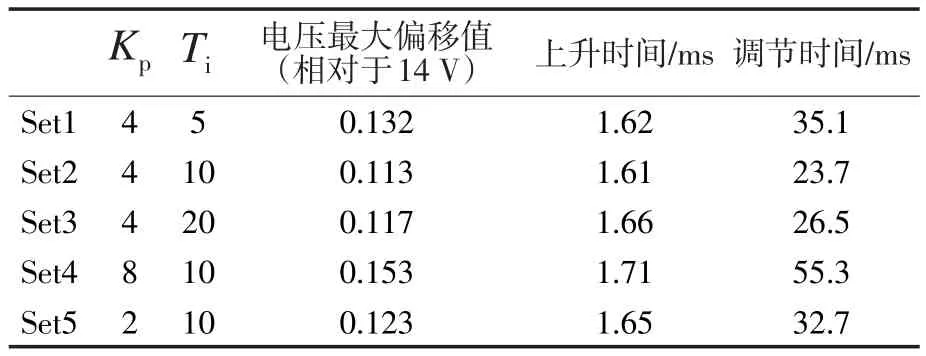
表1 对应的部分仿真结果数据Tab.1 Partial data of corresponding simulations

从仿真中得到的实验数据，不仅证实各个环节建模的正确性，而且为建立实际控制系统提供有效调整参数，并在此基础上通过工程整定进行修正，从而达到理想的实验结果，实现系统设计的目标。

3 实验结果与应用分析

为了进一步证明该浮充策略的有效性，搭建了一套基于改进型Buck电路的光伏充电控制器，在此基础上进行实验验证。实验系统主控芯片采用TMS320F28016数字信号处理器。由图6所示，该充电控制器由一个三相Buck转换器构成，其开关控制信号由主控芯片进行调节控制。实验系统中充电过程快速地在3个阶段交叉进行，如此设计可以达到有效降低系统输出纹波的效果。

图6 实验中采用的太阳能充电系统Fig.6 Solar charge controller used in the experiment

实验系统中由稳压源模拟光伏电池板，接入到充电控制器的PV连接端，作为充电能量输入。此外在实验过程中要保证蓄电池剩余电量接近满荷状态（SoC大于91%），并通过嵌入程序控制充电控制器，使得充电系统处于浮充状态下。

为证明本文采用的浮充控制方法在光伏发电系统中的有效性，设计实验过程如下：程控电源初始设置模拟光强为300 W/m2对应的15.13 V电压；待充电稳定运行后进行光照强度突变测试，即瞬时调整电源至700 W/m2光强对应的21.37 V电压。设定蓄电池浮充稳态电压为14.03 V（室内25℃温度补偿后结果），如图7所示，实验结果反映在浮充充电阶段中，充电系统在充电启动时和PV能量输入端大幅变化时对蓄电池充电电压和电流的控制。其中由图7可以看出，在系统启动充电650 ms后，充电电压稳定在14 V附近，以0.95 A充电电流开始进行浮充充电，反应了系统反馈回路不仅可以保持有效的涓流充电，也能保证充电电压稳定在浮充电压点并避免蓄电池的过充。图7显示光照强度发生阶跃变化后，充电电压在220 ms后爬升到最大点14.18 V，然后经过系统PI反馈环节的调节在1.625 s后返回到稳定浮充电压，反映出系统对光强大幅变化而引起的输入扰动的快速抑制能力。

图7 实验结果Fig.7 Results of experiment

完成实验验证后，对该套光伏充电系统进行户外应用测试，其中，将系统PV输入端接入型号为SNM-M85的85 Wp太阳能电池板，并考虑到户外测试环境的温度变化，对浮充电压点进行温度补偿系数为-18 mV/℃的实时修正。在春季某天的整个白昼内，通过对系统关键信号的采样搜集，绘制应用测试结果如图8所示。

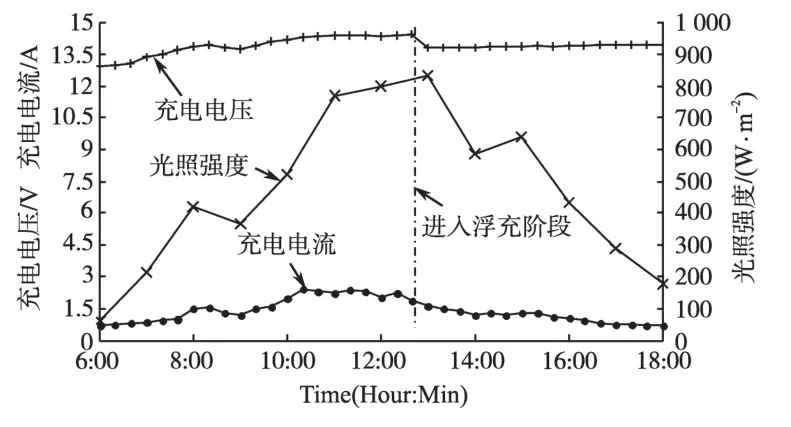
图8 户外实际应用测试结果Fig.8 Outdoor test of the battery charging control system

户外实际应用测试结果验证了本文设计的浮充控制方法的有效性和可靠性，如图8所示。通过充电系统的控制，在充电进入浮充阶段后充电电压始终没有超过最大浮充电压14.18 V（温度补偿后），避免了过充现象的发生；并且保持最低有效充电电压高于13.5 V，充分保证了在白天光照条件下对蓄电池的最大容量形式充电。

4 结论

为使独立光伏充电系统中提高铅酸蓄电池有效使用寿命和避免过充现象，本文通过分析充电系统中各个环节工作特性，设计并实现了一种高效稳定的浮充控制方法。该控制方法是通过建立在稳定浮充电压点的系统各环节动态模型来完成设计的，并在一套以TMS320F芯片控制的Buck充电控制电路上进行了实验验证。从实验结果可以看出，通过以PI算法控制PWM调制信号的反馈调节作用，充电系统有效地防止了由于光照强度突变引而起的过充现象；并且保持浮充状态下的涓流充电方式，保证了电池额定容量的利用最大化，从而大幅提高蓄电池有效使用寿命。

［1］吴理博，赵争鸣，刘建政，等.独立光伏照明系统中的能量管理控制［J］.中国电机工程学报，2005，25（22）：68-72.

［2］Huang B J，Hsu P C，Wu M S，et al.System Dynamic Model and Charging Control of Lead⁃acid Battery for Stand⁃alone So⁃lar PV System［J］.Solar Energy，2010，84（5）：822-830.

［3］廖志凌，阮新波.一种独立光伏发电系统双向变换器的控制策略［J］.电工技术学报，2008，23（1）：97-103.

［4］Muneret X.Influence of Float and Charge Voltage Adjustment on the Service Life of AGM VRLA Batteries Depending on the Conditions of use［J］.Power Sources，2005，144（2）：322-328.

［5］欧阳名三.独立光伏系统中蓄电池管理的研究［D］.合肥：合肥工业大学，2004.

［6］肖鹏，陈国呈，吴春华，等.一种新型光伏独立发电系统研究［J］.电气传动，2008，38（8）：32-43.