三－自相似集的一种分类及其解析表达

钟世萍 杨光俊

(云南大学 数学系，昆明 650091)

自相似性是分形几何的一个基本特征，分形的自相似性是指分形的某一个局部在各个方向上按相同的比例放大后其形态和整体相似。无论怎样压缩尺度，这一局部总是存在更精细的结构，并且其构造总是与整体相似。自相似性的产生是由于分形的构造过程可简单地归为“从初始元变为生成元”的过程，那么当压缩是相似压缩时，得到的分形就具有自相似性。用解释的语言来说，就是迭代函数系 (IFS)。Huchinson［1－2］中对此已经做了详细阐述。

Kiko Kawamura［3］考虑了两个自相似压缩所得到的二－自相似集的一种分类，并且给出了很多相关性质。当三个自相似压缩的系数都是实数时，很多学者考虑其相关的性质，详细见文献 ［4－12］。

本文从泛函方程的角度上，考虑三个自相似压缩所得到的三－自相似集，根据三个自相似压缩取共轭的个数，给出三－自相似集的一种分类，并利用小数进位制展开的方法，得到各种情形的一种解析表达。

1 三－自相似集的一种分类

定义1 集合X为三 -自相似集，当且仅当非空紧集X⊂C满足

X= ψ1(X)∪ ψ2(X)∪ ψ3(X)，

其中ψ1，ψ2，ψ3是复数C上的相似压缩。

相似压缩的定义如下:

设一个映射ψ:Rn→Rn是相似压缩［13］当且仅当存在一个常数L(ψ)∈(0，1)，使得

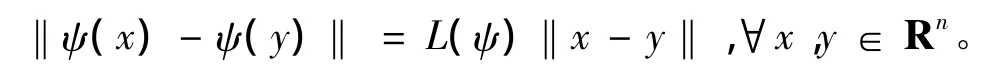
根据三个自相似压缩取共轭的个数，三－自相似集主要可以分成以下四种不同情况。第一种情况是三个都不取共轭;第二种是三个都取共轭;第三种是三个中有二个取共轭;第四种是三个中有一个取共轭。在这里，为了研究方便，在考虑三个取二个共轭时，我们只考虑第一和第三个取共轭;在考虑三个取一个共轭时，我们只考虑第二个取共轭。具体如下:

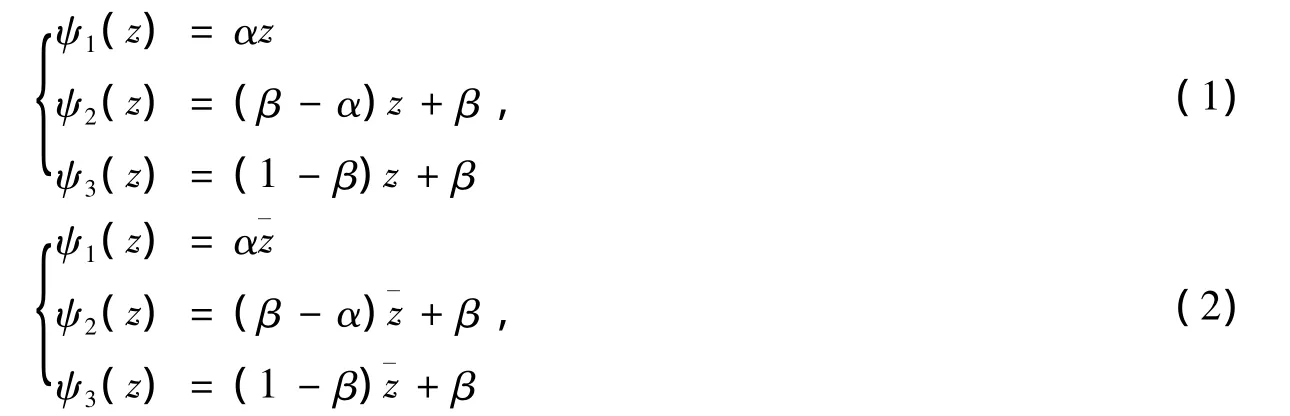
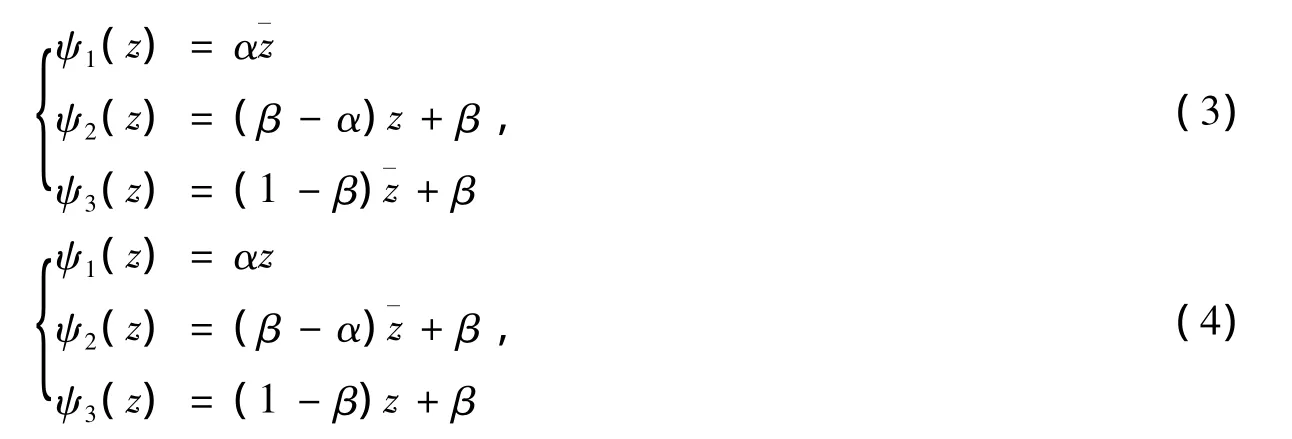
其中复参数α，β满足|α|＜1，|β-α|＜1，|β|＜1。

现在，我们引入下列四个泛函方程。

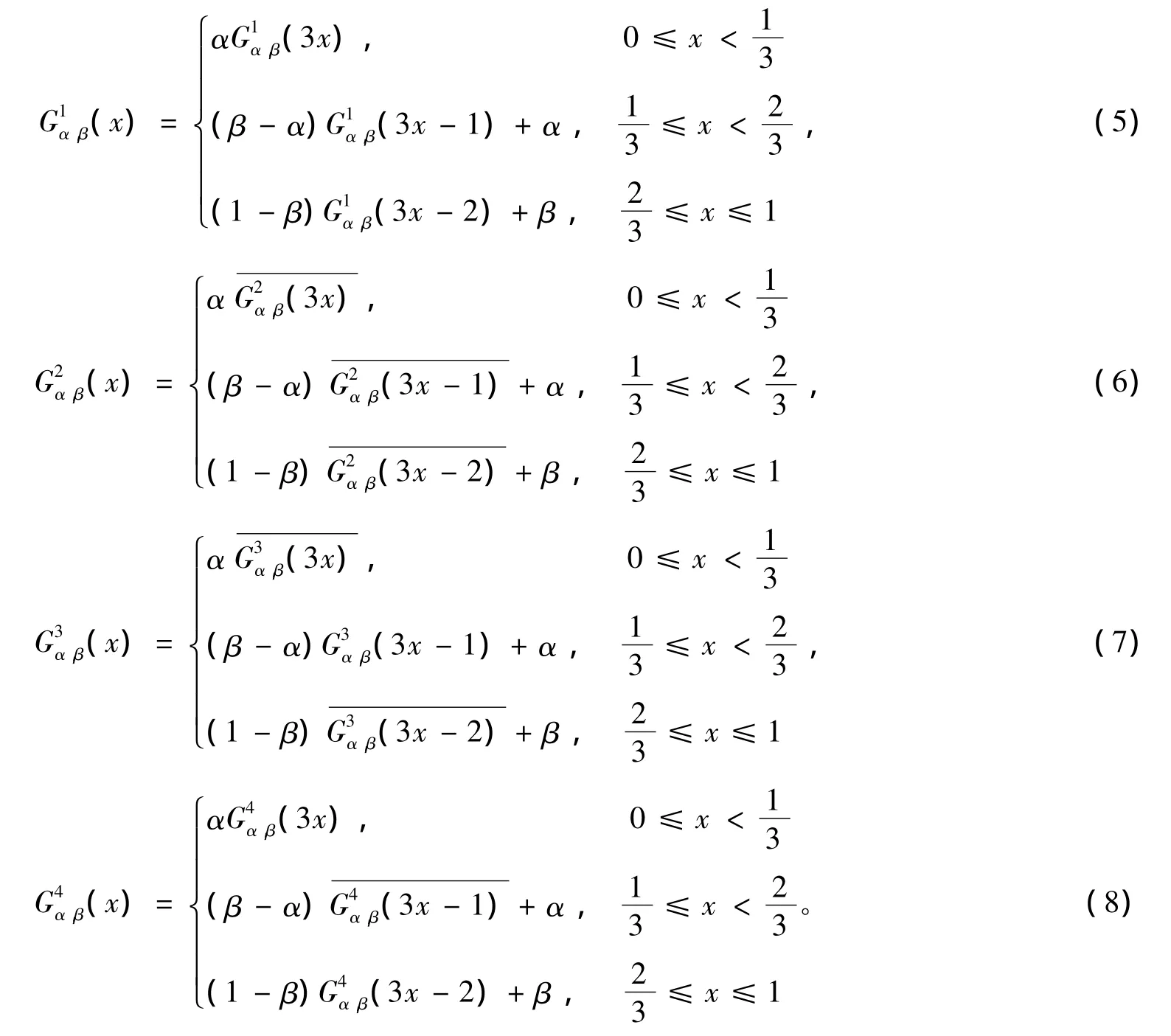
将上述四个泛函方程 (5)～(8)分别等价于下列泛函方程。

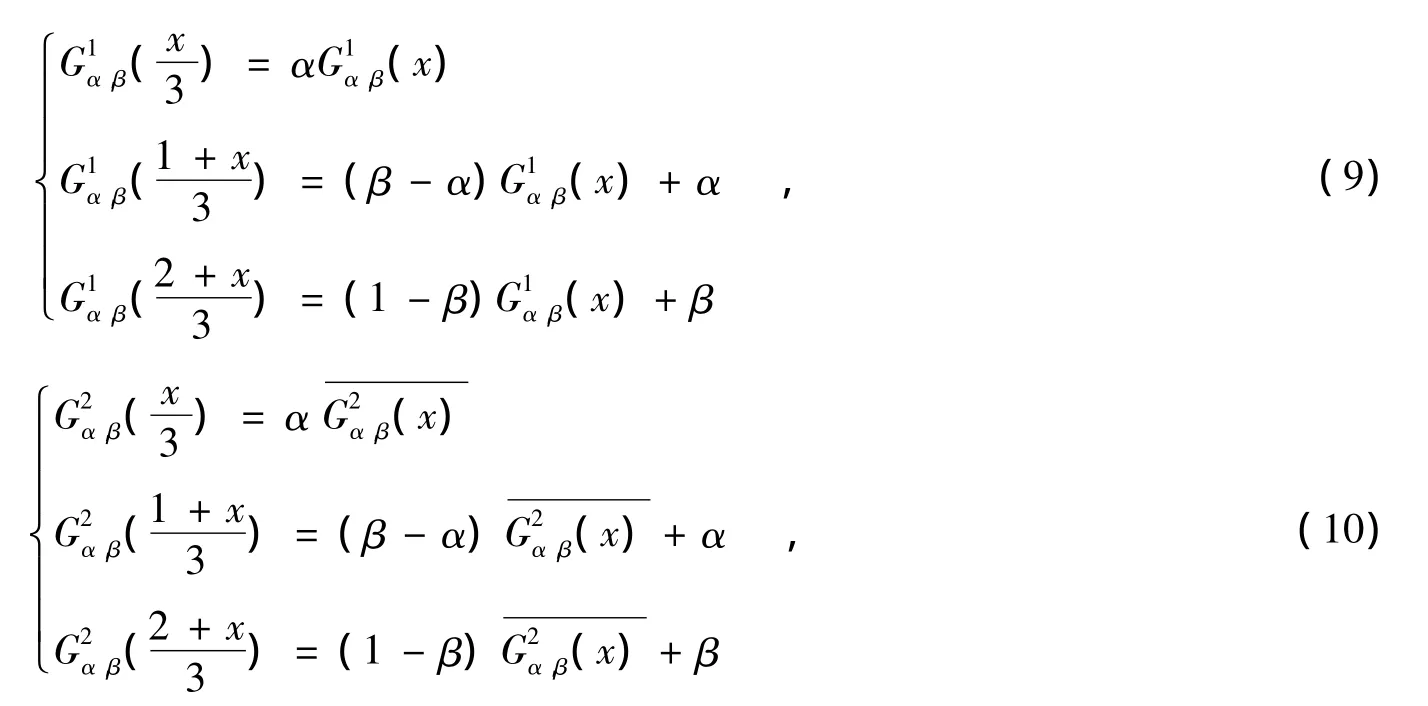
我们注意到 H．Okamoto 和 M．Wunsch［4－5］研究了下列泛函方程

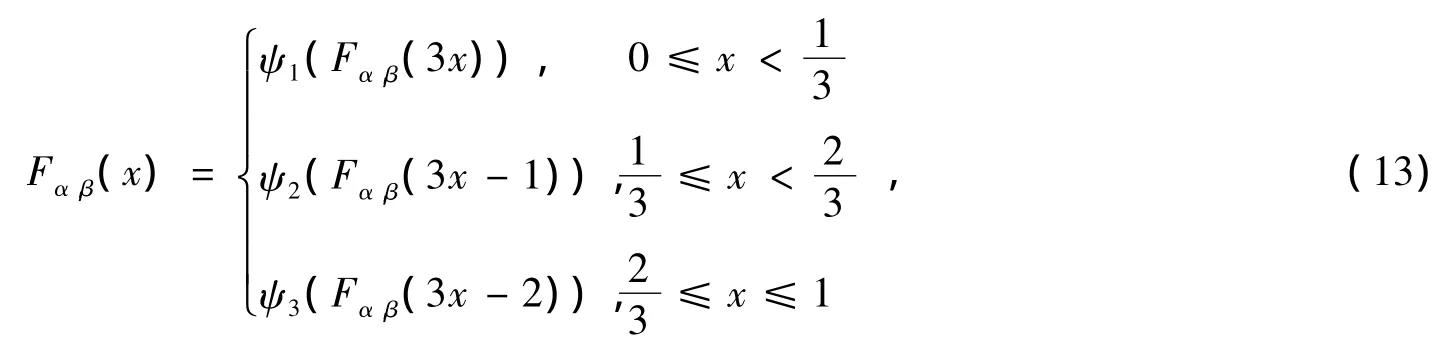
其中 ψ1，ψ2，ψ3满足式(1)。

Okamoto注意到，Fα，β(x)在区间上［0，1］上连续，且当α，β取不同的值时，Fα，β(x)可以与一些著名的函数联系起来。比如说，当和时，Fα，β(x)分别是 Perkins［7］和 Bourbaki［8］定义的处处不可微函数(如图1和图2示)。同时，当时，Fα，β(x)是 Cantor－ Lebesgue奇异函数(如图3示)。

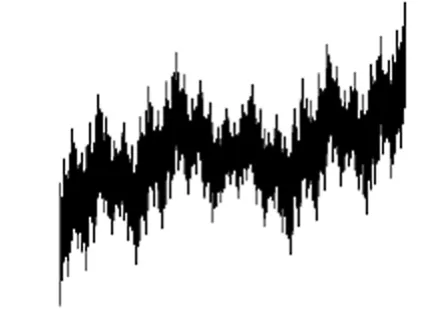
图1 perkins函数

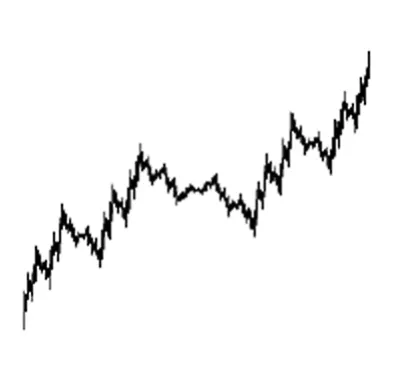
图2 Bourbaki函数

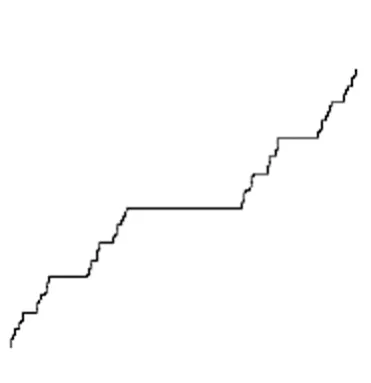
图3 Cantor－Lebesgue函数

设 x∈［0，1］，将［0，1］之间的数用0px1x2…xk…(xk∈ {0，1，2，…，p-1})的形式表示出来就叫做 x的p进位表示。事实上，所谓p进位小数展开就是将x∈［0，1］表示成级数形式，即

其中，p称为小数进位制的“基”，x的第k位小数xk为该基上的展开系数。

例如，当p=3时，x的3进位写成级数形式为

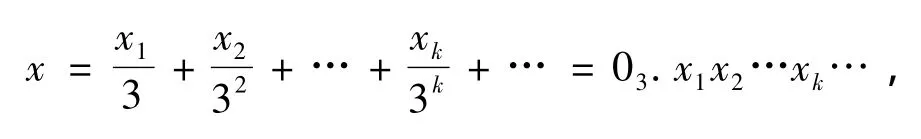
其中，xk∈ {0，1，2}。

我们记:αR是α的实部，αⅠ是α的虚部。类似地，记βR和βⅠ分别为β的实部和虚部。pn=#{xi=0:i=

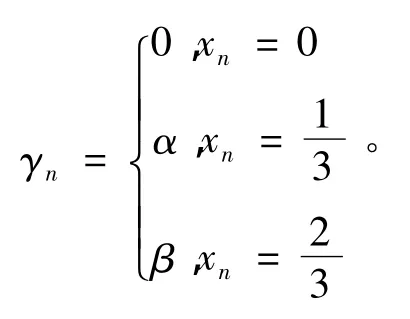
引理 1 设 xi，xi'∈ {0，1，2}，i=1，2，…，n。

(1)当 x1'=0，xi'=xi-1，i≥2 时，

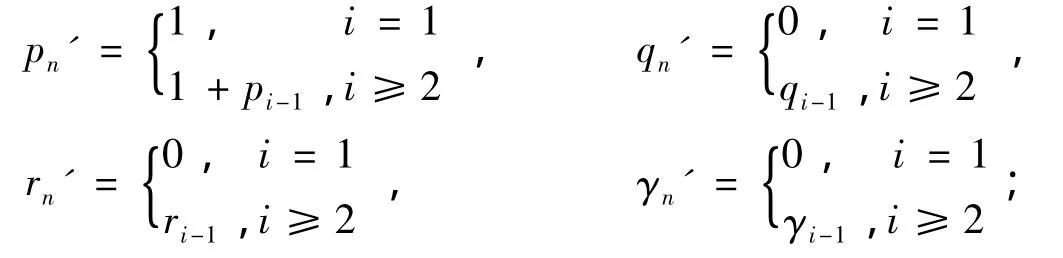
(2)当 x1'=1，xi'=xi-1，i≥2 时，

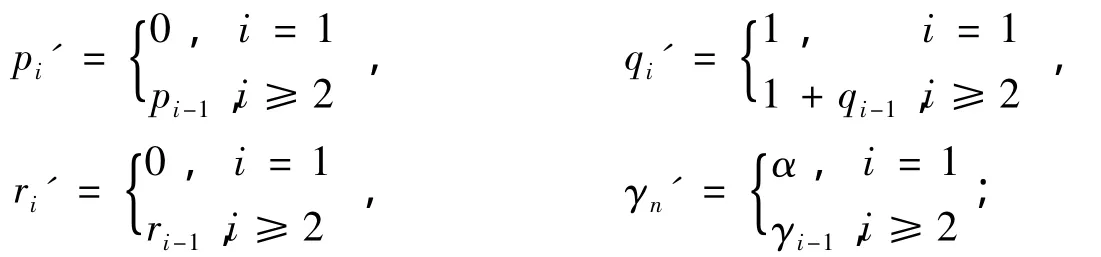
(3)当 x1'=2，xi'=xi-1，i≥2 时，

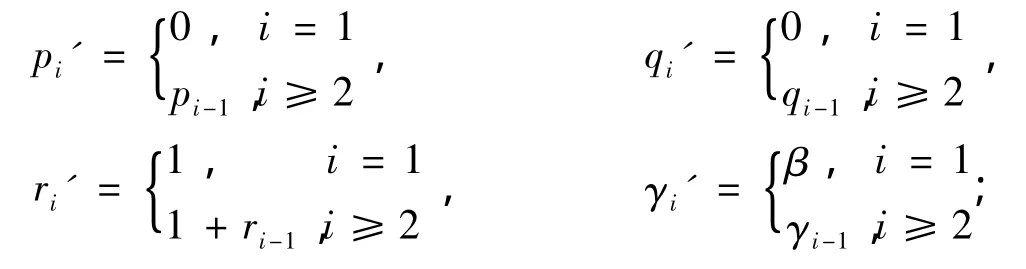
证明:(1)当i=1 时，则x1'=0，p1'=1;当i≥2 时，则pi'=#{xk'=0:k=1，2，…，i}=1+#{xk-1=0:k=2，3，…，i}=1+#{xk=0:k=1，3，…，i-1}=1+pi-1。其余 pi'，ri'，γi'的定义即可得到。(2)、(3)类似可证。

定理2 满足泛函方程(5)的解是唯一的，并且是有界的，其解析解可以写为

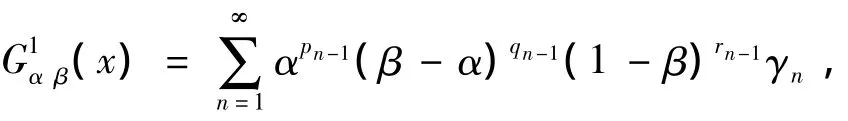
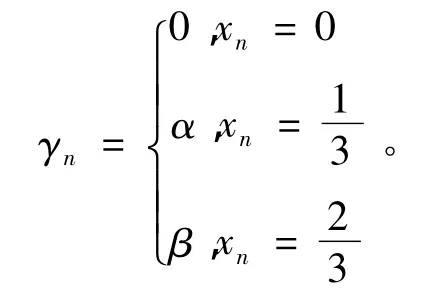
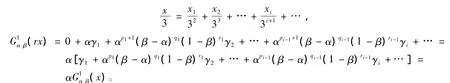
对于第二个方程，根据引理1(2)，类拟有

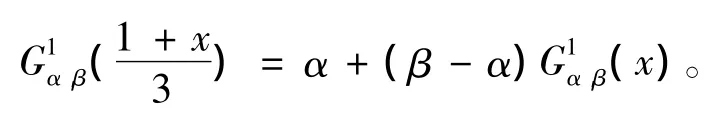
对于第三个方程，根据引理1(3)，类拟有

接下来，我们来证明唯一性。设B(Ⅰ)为定义在区间Ⅰ实有界函数所组成的Bananch空间，其范数为。设

T:B(Ⅰ)→ Ⅰ，g → T(g)，

其中T(g)满足

因此，T是压缩因子为c:=max{α，β-α，1-β}的压缩映射。事实上，我们记hi:=T(gi)，∀qi∈B(Ⅰ)，i=1，2，我们容易计算有

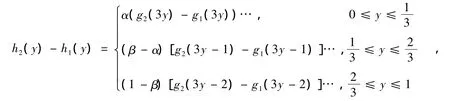
根据压缩映射原理知，T在Ⅰ上有唯一的不动点。因此，我们有唯一的有界解(x)满足此泛函方程。

我们考虑满足泛函方程(7)的一种解析表达式。

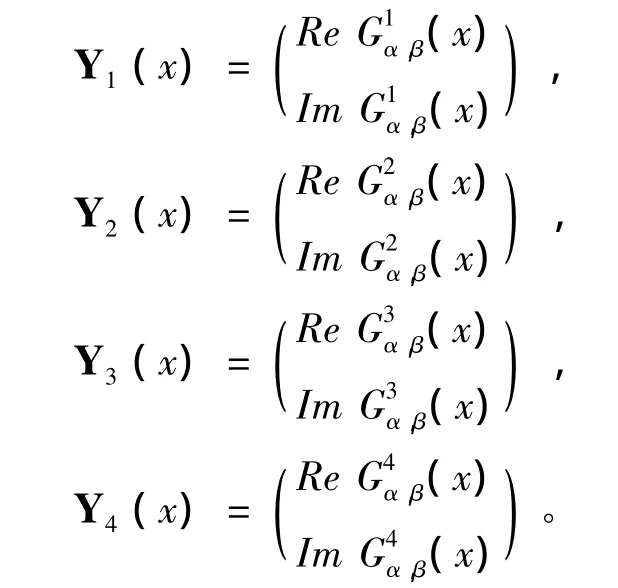
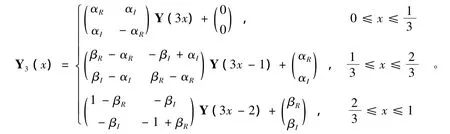
因此，我们得到下面定理。

定理3 满足泛函方程 (7)的解是唯一的，并且是有界的，其解析解可以写为

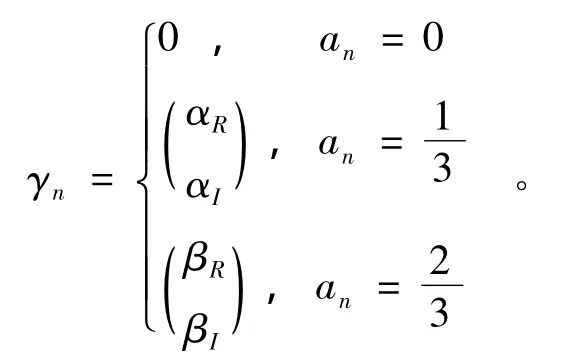
采用类似的方法，我们也能得到G4α，β(x)的解析表达式。

定理4 满足泛函方程 (8)存在唯一的，并且是有界的，其解析解可以写为

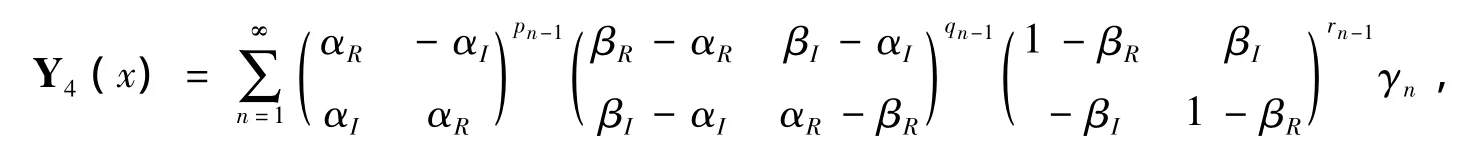
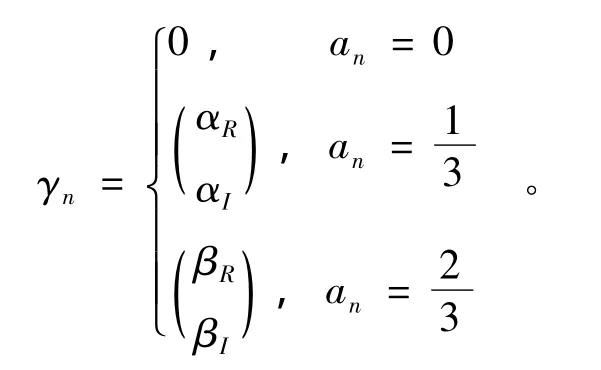
［1］Hutchinson J E．Ein einfaches beispiel fur eine funktion welche uberall stetig und nichtdiereezierbar ist［J］．Math hys，1996(13):216 －221．

［2］Hutchinson J E．Fractals and self－ similarity［J］．Indiana University Math Journal，1982，30(5):713 －747．

［3］Kawamura K．On the classification of self－ similar sets determined by two contractions on the plane［J］．J Math Kyoto Univ，2002，42(2):255－286．

［4］Okamoto H．A remark on continuous，nowhere dierentiable functions［J］．Proc Japan Acad Ser A Math Sci，2005，81(3):47 － 50．

［5］Okamoto H，Wunsch M．A geometric construction of continuous，strictly increasing singular functions［J］．Proc Japan Acad Ser A Math Sci，2007，83(7):114 －118．

［6］Sánchez Juan Fernández ，Viader Pelegri，Paradis Jaume，et al．A singular function with a non － zero finite derivative on adense set［J］．Non-linearAnal，2014，95:703 －713．

［7］Perkins F W．An elementary example of a continuous nondifferentiable functions［J］．Amer Math Monthly，1927，34:476 －478．

［8］Nicolas Bourbaki．Functions of a Real Variable:Elementary Theory［M］．Berlin:Springer，2004．

［9］Kenta Kobayashi．On the critical case of Okmamoto’s continuous non-differentiable functions［J］．Proc Japan Acad Ser A Math Sci，2009，85(8):101－104．

［10］Lewis Thomas M．Aprobabilistic property of Katsuura’s continuous nowhere differentiable function［J］．J Math Anal，2009，353:224 －231．

［11］Hidefumi Katsuura．Continuous nowhere － differentiable functions－ an application of contraction mappings［J］．American Mathematical Monthly，1991，98(5):411 －416．

［12］Dorfman J R，Gilbert Themas．Statistical properties of r－ adic processes and their connections to families of popular fractal cures［J］．Perspectives of Nonequilibrium Statistical Physics，2011，97(3):357 －369．

［13］Kenneth Falconer．Fractal Geometry － Mathematical Foundationsand Applications［M］．Chichester:Wiley，2003．

［14］Barnsley M．Fractals Everywhere［M］．SaltLake City:Academic Press，1988．

［15］Gerald．Measure Edgar，Topology，and Fractal Geometry［M］．NewYork:Springer，2008．