带积分边值条件的分数阶微分方程解的存在性和唯一性
刘 帅, 贾 梅, 秦小娜
(上海理工大学理学院,上海 200093)
带积分边值条件的分数阶微分方程解的存在性和唯一性
刘 帅, 贾 梅, 秦小娜
(上海理工大学理学院,上海 200093)
研究了一类带积分边值条件的分数阶微分方程边值问题解的存在性和唯一性,并利用Schauder不动点定理以及压缩映像原理,得到了边值问题解的存在性及唯一性结论.
积分边值条件;不动点定理;存在性和唯一性
1 问题的提出
在实际的研究中,许多数学和物理学问题都归结为微分方程边值问题,如波动方程等,因此,学者们对微分方程边值问题进行了大量研究,得到了许多有意义的结论[1-2].近年来,由于分数阶微分方程在化学工程、热弹性力学以及人口动态等问题中得到了很好的应用,受到人们的广泛关注[2-16].带积分边界的分数阶微分方程边值问题更是成为最近几年研究的热点问题,并且得到了许多的结论[4-9].
本文研究在非线性项中含有分数阶导数的带有积分边界条件的边值问题:解的存在性和唯一性,其中,1<λ≤2,0<σ<1且λ-σ-1>0,α1,α2,β1,β2∈R,且δ=α1α2+ α1β2-α2β1≠0,g1,g2∈L1([0,1],R+),,为Caputo导数.
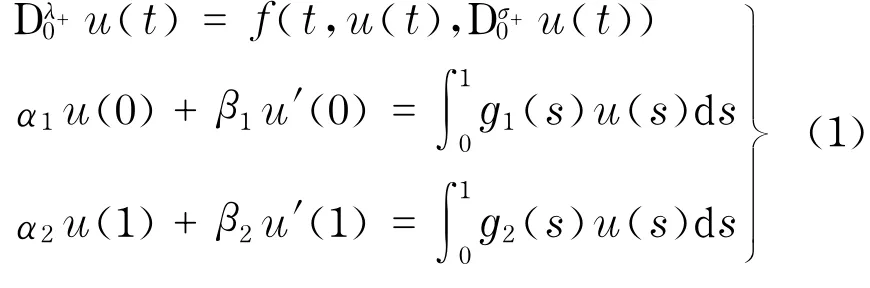

从上面的分析可以看出,带积分边界条件的分数阶微分方程的相关研究成果已经很多,文献[13]对边界条件中系数的符号进行了限制,而本文研究的内容其系数具有任意性,是在文献[13]的基础上进一步的推广,更具有普遍性.

a.对一切的x,y∈R,f(·,x,y)是[0,1]→R可测函数;
b.对几乎处处的t∈[0,1],f(t,·,·)是R× R→R的连续函数;

本文所涉及到的f都是Lq-Caratheodory函数.
2 预备知识
定义1[2]函数y:[0,∞)→R的α阶积分定义为

对任意的α>0,右端积分在[0,∞)上逐点可积.
定义2[2]函数y:[0,∞)→R的α阶Caputo型导数定义为
其中,α>0,α不为整数,右端积分在[0,∞)上逐点可积,n=[α]+1,[α]为不超过α的最大整数.当α>0,α为整数时,=y(α)(t).
引理1[3]阶数为α的分数阶微分方程x(t)=0的一般解为

引理2 设y∈Lq[0,1],且1<λ≤2,0<σ<1,则当ω≠0时,边值问题



引理3 G,Gσ,H1,Hσ1在t,s∈[0,1]上是连续且有界的.
借助引理3的结论,为研究问题方便起见,作如

引理4 设f是Lq-Caratheodory函数,则T:X→X是全连续的.
证明 a.T为连续的.
设{un}⊂X,u∈X,满足当n→∞时,‖unu‖→0.因此,对a.e.s∈[0,1],有




由Ascolli-Arzela定理可知,T相对紧.综上所述,T:X→X是全连续的.
3 解的存在性定理


所以,‖Tu‖≤r.故有T(Br)⊂Br.
由引理4可知,T为全连续的.根据Schauder不动点定理可知,T在Br中至少存在1个不动点.
故边值问题(1)在X中至少存在1个有界解.
定理2 设f是Lq-Caratheodory函数,且满足(H2),则边值问题(1)在X中至少存在1个有界解.
证明 取,


所以,‖Tu‖≤r.故有T(Br)⊂Br.
由引理4可知,T为全连续的.根据Schauder不动点定理可知,T在Br中至少存在1个不动点.
故边值问题(1)在X中至少存在1个有界解.
定理3 设f是Lq-Caratheodory函数,且满足(H3),则边值问题(1)在X中至少存在1个有界解.


所以,‖Tu‖≤r.故有T(Br)⊂Br.
由引理4可知,T为全连续的.根据Schauder不动点定理可知,T在Br中至少存在1个不动点.
故边值问题(1)在X中至少存在1个有界解.
4 解的唯一性定理
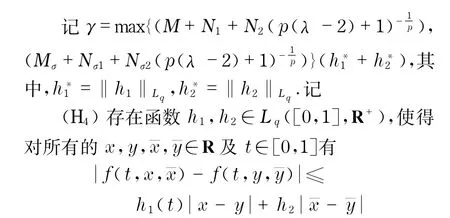
定理4 若(H4)成立,且0<γ<1,则边值问题(1)有唯一解.
证明 任取u,v∈X,对t∈[0,1]有

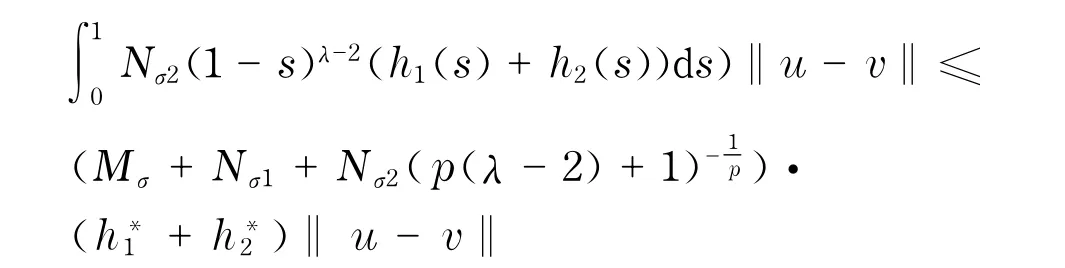
所以,‖Tu-Tv‖≤γ‖u-v‖,由于0<γ<1,根据压缩映像原理可知,T在X中存在唯一不动点.
故边值问题(1)在X中有唯一解.
[1] 葛渭高.非线性常微分方程边值问题[M].北京:科学出版社,2007.
[2] Podlubny I.Fractional differential equations[M].New York:Academic Press,1999.
[3] Zhnag X M,Feng M Q.Positive solutions for a class of 2nth-order singular boundary value problems[J]. Nonlinear Analysis,2008,69(4):1287-1298.
[4] Ahmad B,Nieto J J.Existence results for nonlinear boundary value problems of fractional integrodifferential equations with integral boundary conditions[J].Boundary Value Problems(Hindawi),2009:708576.
[5] Ahmad B,Nieto J J,Alseaedi A.Existence and uniqueness of solutions for nonlinear fractional differential equations with non-separated type integral boundary conditions[J].Acta Mathematic Scientia,2011,31(6):2122-2130.
[6] Hu M,Wang L L.Existence of solutions for a nonlinear fractional differential equation with integral boundary condition[J].International Journal of Mathematical and Computer Science,2011(7):1-7.
[7] Benchohra M,Ouaar F.Existence results for nonlinear fractional differential equations with integral boundary conditions[J].Bulletin of Mathematical Analysis and Applications,2010(2):7-15.
[8] Liu X P,Jia M,Wu B F.Existence and uniqueness of solution for fractional differential equations with integral boundary conditions[J].Electronic Journal of Qualitative Theory of Differential Equations,2009 (69):1-10.
[9] 金京福,刘锡平,窦丽霞,等.分数阶微分方程积分方程边值问题正解存在性[J].吉林大学学报(理学版),2011,49(5):823-828.
[10] Agarwal R P,O’Regan D,Staněk S.Positive solutions for dirichlet problems of singular nonlinear fractional differential equations[J].Journal of Mathematical Analysis and Applications,2010,371(1):57-68.
[11] Ahmad B,Ntouyas S K.Existence results for nonlocal boundary value problems of fractional differential equations and inclusions with strip conditions[J]. Boundary Value Problems(Springer),2012:55.
[12] Guezane-Lakoud A,Khaldi R.Solvability of a fractional boundary value problem with fractional integral condition[J].Nonlinear Analysis:Theory Method& Applications,2012,75(4):2692-2700.
[13] Khan R A,Rehman M U,Henderson J.Existence and uniqueness of solutions for nonlinear fractional differential equations with integral boundary conditions[J].Fractional Differential Calculus,2011,1(1):29-43.
[14] 窦丽霞,刘锡平,金京福,等.分数阶积分微分方程多点边值问题解的存在性和唯一性[J].上海理工大学学报,2012,34(1):51-55.
[15] 王淑,贾梅,祁卫杰.非线性项变号的分数阶微分方程边值问题正解的存在性[J].上海理工大学学报,2013,35(1):1-6.
[16] Feng M Q,Zhang X M,Ge WG.New existence results for higher-order nonlinear fractional differential equation with integral boundary conditions[J]. Boundary Value Problems(Hindawi),2011:720702.
(编辑:石 瑛)
Existence and Uniqueness of Solutions of the Fractional Differential Equation with Integral Boundary Value Conditions
LIUShuai, JIA Mei, QIN Xiao-na
(College of Science,University of Shanghai for Science and Technology,Shanghai 200093,China)
The existence and uniqueness of solutions were studied for a class of fractional differential equations with integral boundary value conditions.The conclusions about the existence and uniqueness of solutions were obtained by using the Schauder fixed point theorem and the Banach contraction principle.
integral boundary value condition;fixed point theorem;existence and uniqueness
O 175.8文献标示码:A
1007-6735(2014)05-0409-07
10.13255/j.cnki.jusst.2014.05.001
2013-07-21
国家自然科学基金资助项目(11171220);上海市教委科研创新基金重点资助项目(10ZZ93)
刘 帅(1987-),女,硕士研究生.研究方向:应用微分方程.E-mail:liushuai871030@163.com
贾 梅(1963-),女,副教授.研究方向:应用微分方程.E-mail:jiamei-usst@163.com

