高阶传动误差斜齿轮修形设计与加工

蒋进科，方宗德，苏进展

（西北工业大学机电学院，710072西安）

高阶传动误差斜齿轮修形设计与加工

蒋进科，方宗德，苏进展

（西北工业大学机电学院，710072西安）

为了提高齿面啮合性能，降低磨削误差，设计高阶传动误差与接触路径曲线，并结合承载接触分析（LTCA）通过优化承载传动误差（LTE）幅值最小确定待定的参数，根据齿条展成渐开线齿面原理，求解小轮法向拓扑修形曲面；建立基于成形砂轮轴向廓形与5轴联动CNC机床各轴运动敏感性分析的齿面修形模型，判断砂轮与齿面的接触状态，计算磨削误差，应用PSO优化算法得到机床各轴运动参数与砂轮廓形的修形曲线.算例表明：优化的高阶传动误差在曲线转换点处是相切连接的，其拓扑修形曲面在啮入端近齿根、啮出端近齿顶处有较大的修形量，修形区域近似对角；中部有一定微小内凹的高阶传动误差可降低LTE幅值，减小轮齿振动，其内凹量大小与齿轮副工况有关，随载荷增加，最佳内凹量逐渐增大；经过成形砂轮进行主要的修形磨削及平面砂轮进行辅助的对角修形磨削可实现拓扑修形齿面加工，理论磨削误差小于2μm.

斜齿轮；拓扑修形；高阶传动误差；数控磨削；成形砂轮

齿面印痕和传动误差（TE）已被证实是衡量轮齿啮合质量的重要指标［1-3］.通过齿轮接触分析（TCA）［4］、承载接触分析［5］（LTCA）获得轮齿几何传动误差、齿面印痕及承载传动误差（LTE），为高精度齿轮的啮合分析提供了重要依据.

高阶传动误差曾用于螺旋齿锥齿轮等复杂齿面的啮合分析，并且已在生产加工中得到应用［6-9］，其较传统的二阶传动误差在降低振动和噪音方面有明显优点，且强度不会受到太大影响.国内外学者针对复杂齿面的CNC高阶修正技术进行了大量研究，主要包括:基于摇台型机床的齿面误差修正［10］，但可调加工参数有限，不能实现高精度误差修正；基于CNC机床各轴运动敏感性分析的齿面修正［11-16］，可实现高阶修正，但求解方法较为困难；文献［17］提出了一种预设二次抛物线几何传动误差与接触路径的螺旋齿锥齿轮拓扑修形加工方法，文献［18］提出了优化LTE幅值的准双曲面齿轮修正方法.以上研究均未考虑到几何传动误差在啮合转换点处的夹角对轮齿啮合性能影响，且针对斜齿轮高阶传动误差的设计与成形磨齿加工研究较少.随着多轴数控技术的发展，平面砂轮、成形砂轮的磨齿精度已达2级［19］，为高精度渐开线圆柱齿轮磨齿加工创造了条件.

作者以一对齿轮副为例，大轮为理论齿面，结合TCA、LTCA设计了四阶几何传动误差与齿面接触迹线，通过优化LTE幅值最小确定了其参数；根据齿条展成齿轮运动关系，反算小轮的法向修形曲面；建立基于砂轮廓形与各轴运动敏感性分析的5轴联动CNC成形砂轮磨齿加工模型，通过粒子群（Particle swarm optimization，PSO）优化算法，求解各轴运动参数及砂轮廓形，有效降低了齿面振动及磨削误差.

1 斜齿轮高阶传动误差的修形设计

1.1 高阶传动误差曲线设计

本文高阶传动误差的修形设计以TCA的几何传动误差控制为主，综合考虑齿面啮合印痕的设计.设计思路为:1）高阶几何传动误差曲线设计不能降低齿面的设计重合度；2）为了减小啮入啮出冲击，以靠近齿宽中部某点为参考点（见图1（a）中的p0点）在接近啮入啮出端尽可能有足够的抛物线传动误差，为保证啮合转换点尽可能平滑，中部应有一定的传动误差且形成内凹形状（见图1（a）p1p0p2段曲线）；3）为了避免边缘应力集中，减小齿顶齿根闪温，接触路径尽可能靠近节圆，啮入啮出端接触迹线呈光滑抛物线（见图1（c）的m1m3，m2m4段曲线），且齿根、齿顶需要有一定的齿廓修形（见图1（b）的n1n3，n2n4段曲线）．因此传动误差曲线为

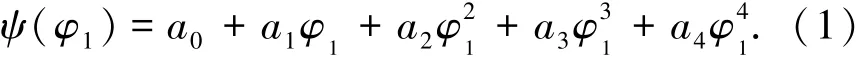
式中:ψ为几何传动误差；φ1为齿轮副啮合过程中主动轮（小轮）转角；a0～a4可通过图1（a）中p0～p4点的数据求解，σ、ε为待定参数；t为常数，根据齿面重合度确定，可取1／3齿宽的啮合周期，λ可取t的一半．

接触迹线可表达为

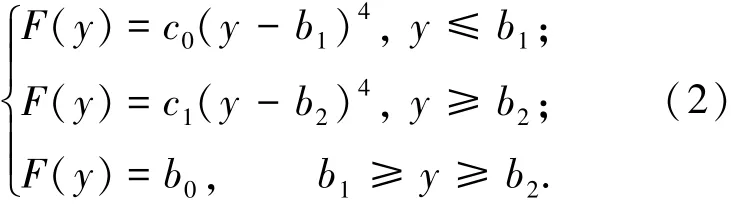
式中:b0～b3为常数，可取齿宽的1／3；c0～c1为常数，通过图1（c）中m0～m4点的数据求解，y为旋转投影面上齿向方向参数．

沿齿廓的修形曲线表达式为

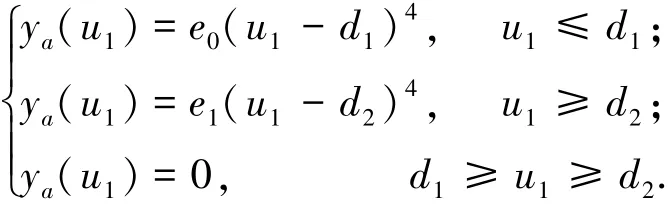
式中:d1、d2为常数，指数取4次，主要修形齿顶、齿根部分．e0～e2通过图1（b）中n1～n2点的数据求解，u1为齿条沿齿高方向参数，q1、q2为待定参数．

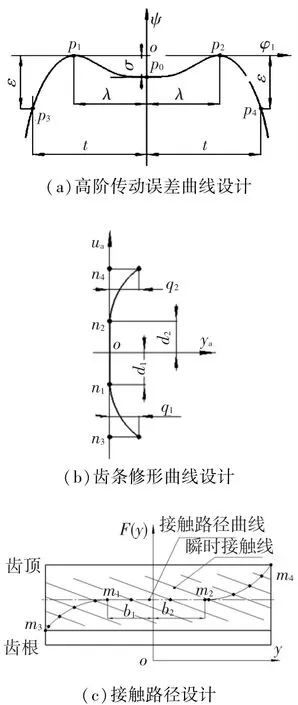
图1 斜齿轮高阶传动误差设计

1.2 高阶传动误差曲线参数的确定

在TCA、LTCA基础上求解一个啮合周期的轮齿法向位移Z，将Z转化为啮合线上位移（LTE），通过优化一个啮合周期的LTE幅值最小确定高阶传动误差的待定参数，目标函数可为

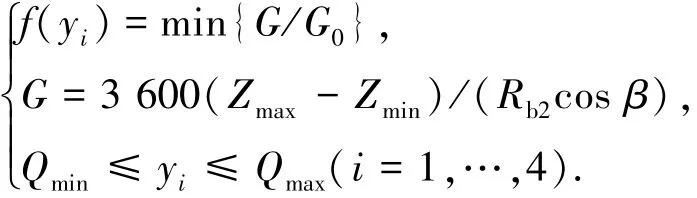
式中:yi为对应于σ、ε、q1、q2的优化变量，Qmin、Qmax为变量范围，G0、G分别为修形前、后承载传动误差幅值，Rb2、β分别为被动大轮基圆半径和螺旋角．

1.3 高阶传动误差的法向修形曲面求解

传统的TCA方程表达式为

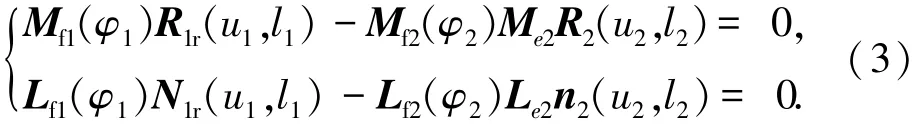
式中:R1r、N1r为小轮齿面位矢及法矢，u1、l1及u2、l2分别为主动小轮、被动大轮齿面参数，Me2为大小轮轴安装误差矩阵，Mf1、Lf1及Mf2、Lf2分别为齿面动坐标系到固定坐标系的转化矩阵，φ2为齿轮副啮合过程中被动轮（大轮）转角．

通过TCA得到几何传动误差表达式为

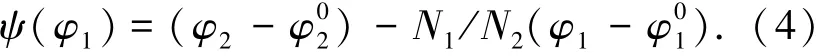
式中:φ1

0、φ20为小轮、大轮初始转角，N1、N2为小轮、大轮的齿数．

文中采用了预设的传动误差和接触迹线，因此齿轮副之间的转角、及齿面印迹点应满足式（1～2）即

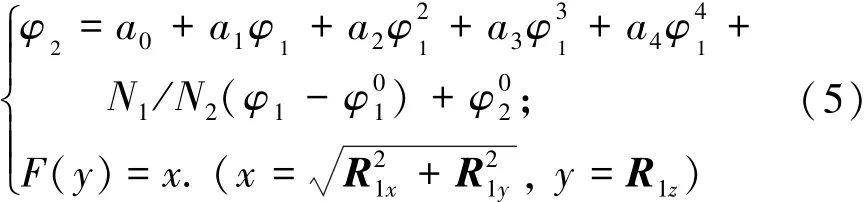
式中R1x、R1y、R1z为小轮齿面位矢分量．

式（3）联立式（5）为高阶传动误差的TCA方程，化简后共有6个方程，取φ1为输入量，求解以u1、l1、u2、l2为未知量的方程组，为了得到确定解，还需再增加2个方程.本文对小轮修形，小轮齿面是齿条刀具切削运动的结果，该过程中:1）齿条刀具廓形是确定的；2）齿条刀具的运动与小轮的运动是关联的，取螺旋角微调与齿条随展成角的移动位移为变量如图2所示，则高阶传动误差的小轮齿面为

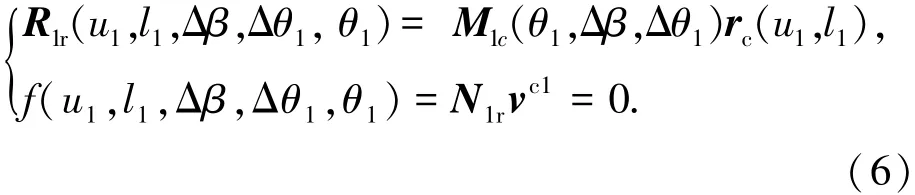
式中:rc为齿条位矢，N1r为齿面位矢，vc1为齿条与小轮相对运动速度，M1c为齿条到齿轮坐标变换矩阵．图2中，rj为工件节圆半径，m为小轮法面模数，Sf为工件固定坐标系，S1为工件动坐标系，Sc为齿条动坐标系，Sa、Sb分别为法向螺旋角β（Δβ为附加螺旋角）与法向压力角αn的参考坐标系，θ1为齿条展成小轮齿面的展成角，Δθ1为附加展成转角．

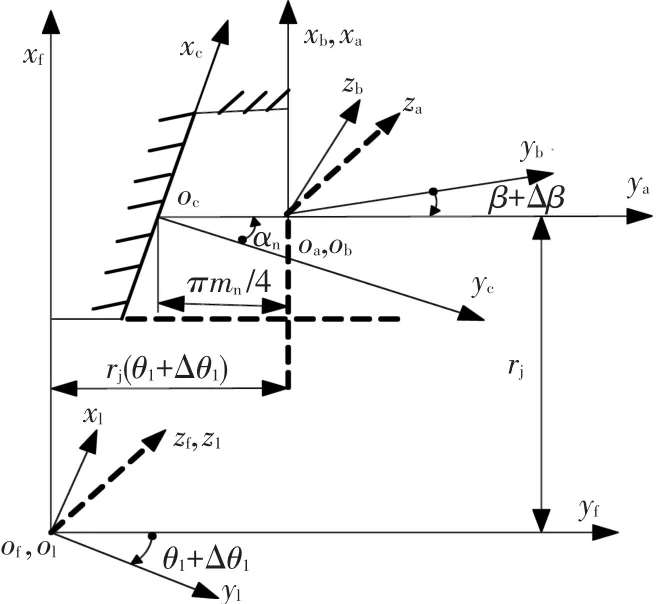
图2 齿条展成渐开线齿面坐标系

式中g0～g6、h0～h6分别为拟合的多项式系数．

小轮修形齿面，可用渐开线齿面与法向修形曲面叠加表示，因此其法向修形曲面为

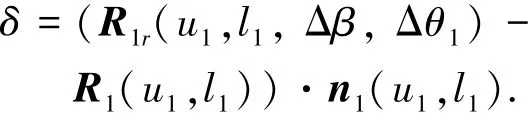
式中R1、n1分别为小轮理论齿面位矢、法矢．

式（3）～（6）联立，取φ1为输入量，可确定6个方程求解以u1、l1、u2、l2、Δβ、Δθ为未知量的方程组，求解出一组小轮齿面参数Δβ、Δθ．小轮齿面是齿条刀具切削运动的结果，将齿条的运动拟合为小轮运动参数的6次多项式函数，即

2 CNC成形砂轮磨削斜齿轮数学模型

2.1 五轴联动CNC成形磨齿机床数学模型

为了便于加工大型渐开线圆柱齿轮，保证机床有足够的刚度，建立图3（a）所示立式5轴联动数控机床模型.按照图3（b）所示成形砂轮磨削齿面运动关系可知被磨削齿面位矢:

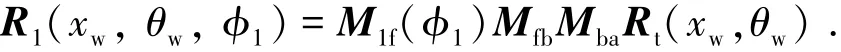
式中:Rt（xw，θw）为成形砂轮位矢，xw、θw为成形砂轮参数；Sf、Sb为参考坐标系；S1为与工件固接坐标系；Sa为螺旋角β参考坐标系；St为与砂轮固接坐标系；φ1为成形砂轮磨齿过程中的斜齿轮旋转角，M1f、Mfb、Mba为从砂轮到被磨削齿面的坐标变换矩阵．

按照图3（c）所示的CNC机床坐标系，磨削后的齿面位矢:

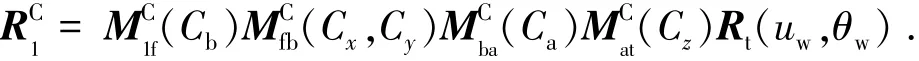
式中:Cx、Cy、Cz分别为3个线性移动轴位移，Ca、Cb、分别为螺旋角回转轴、工件回转轴转角，K1、K2为机床常参数．

图3（c）中，Sf为机床固定坐标系，St为成形砂轮固连坐标系，Sa为螺旋角运动坐标系，Sb为螺旋角运动参考坐标系，S1为工件运动坐标系，

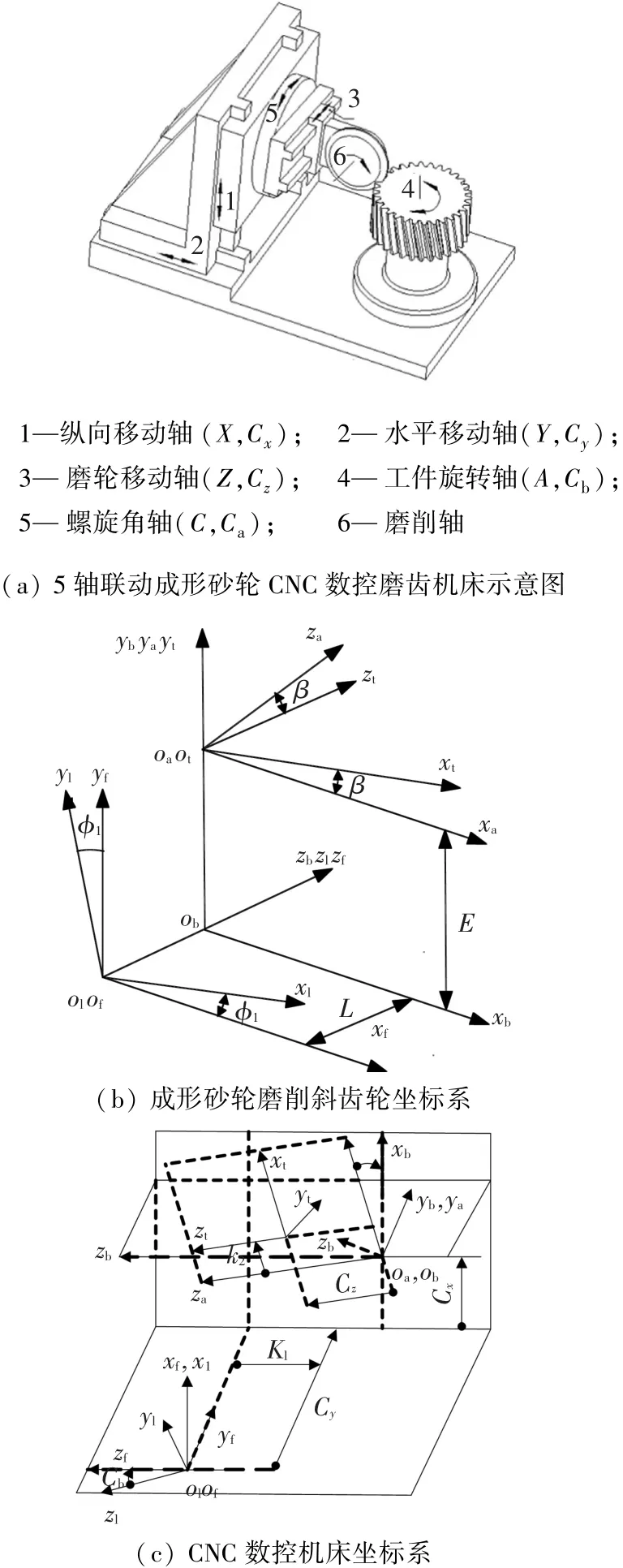
图3 五轴联动CNC数控机床坐标系

从传统型机床向Free-Form型机床运动的等效转换原则是保证刀具与工件的相对位置和姿态在任意时刻都相同，即

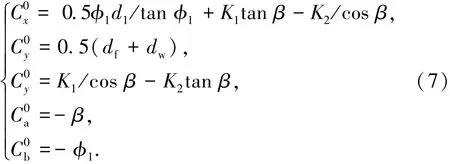
2.2 CNC成形砂轮磨削拓扑修形齿面计算

反求理论齿面的成形砂轮轴向廓形点，通过3次B样条拟合技术得到砂轮廓形曲线，并对其进行修正，其表达式为

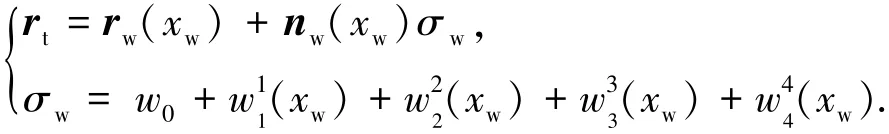
式中:rt为法向修正后的砂轮轴向廓形；σw为法向修正量，w0～w4为修正的系数；rw（xw）、nw为三次B样条拟合的砂轮轴向廓形曲线位矢及单位矢（理论齿面）．

修形曲面（法向偏差）可认为是微调各轴运动参数及砂轮廓形所致，选取φ1为各轴之间的联系参数，实际加工中φ1为时间的线性函数，最高次数6阶，修形曲面表示为

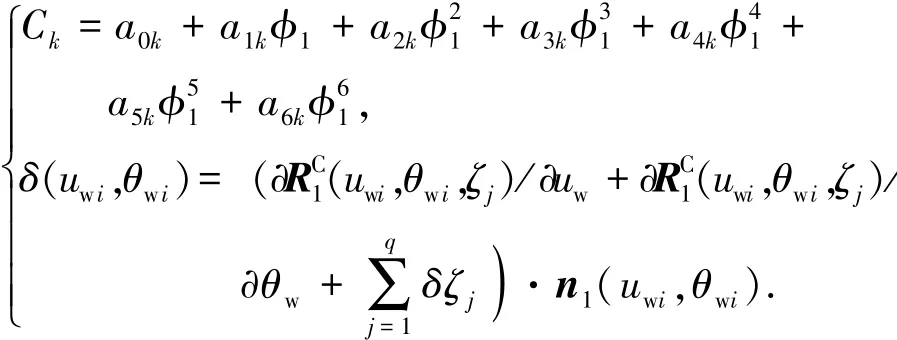
简化用矩阵表示为

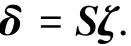
式中:ζ为各轴运动参数Ck（k=x，y，z，a，b）及砂轮修形系数w0～w4，a0x，a1x…a5c，a6c组成的列矢量；S为齿面敏感矩阵，由网格节点i（i=1，…，p，p为齿面网格点数）处各轴敏感系数组成的行矢量Si构成；δ（xwi，θwi为齿面网络节点i处修形量，可通过修形曲面得到．

CNC磨削后的齿面法向修形量、加工误差及各轴运动的变化量为

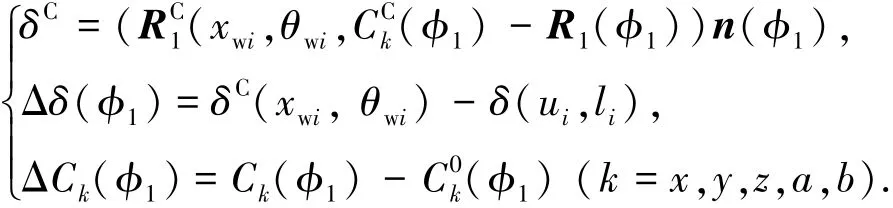
式中:Δδ为CNC修形加工的误差，δC为CNC加工的后的修形量；ΔCk为CNC修形加工各轴运动变化量，Ck、C分别为CNC加工修形齿面与理论齿面的各轴运动曲线．

2.3 砂轮廓形修形参数及机床各轴运动参数求解

粒子群算法（PSO）［20］具有全局收敛性，可求解具有多个局部极值的非线性优化问题，结构简单，易于实现.本文通过PSO优化算法求解式（8）.圆柱齿轮磨齿加工属于减材料（Ease-Off）加工，因此对砂轮是否与齿面接触做出判断:1）Sζ＜0，表示砂轮嵌入齿面i点进行磨削；2）Sζ＞0，表示砂轮远离齿面i点进行磨削；为了使加工误差最小，应使齿面误差平方和最小；设计变量ζi为相应各轴运动及砂轮廓形参数，即w0～w4，a0x，a1x…a5c，a6c，系数总数39个，修形齿面各轴运动系数取值范围为理论齿面各轴系数的微调，因此优化目标为

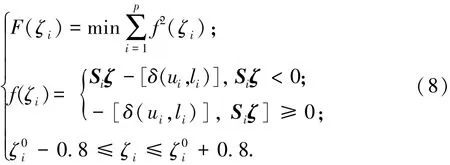
3 算例与分析

以表1标准安装齿轮副为例，大轮额定扭矩为2 500 N·m；取K1=K2=0，dw=200mm；表2中为优化的高阶传动误差曲线参数.图4为TCA、LTCA及五轴联动CNC磨齿仿真结果.

表1 斜齿齿轮副参数

表2 高阶传动误差及齿廓修形曲线优化参数

3.1 啮合性能分析

1）该齿轮副理论重合度为2.29，TCA仿真步长取1／8啮合周期，接触点数为19，因此重合度为（19-1）／8=2.25，接近理论重合度，且从齿根进入，齿顶退出，啮入啮出端有较大的传动误差，齿根、齿顶有一定的修形避免了边缘接触，TE在转换点处相切连接，第2、18个接触点TE为-25″，第9个接触点TE为-3″（见a1、a2）；

2）要实现上述所示的TCA结果，齿条刀具的螺旋角、水平位移在啮入啮出端有较大的运动变化（见b1、b2），法向修形曲面划分为9×15个点（见图4（c）），其主要特征为啮入端、啮出端有较大的修形量；

3）多载荷LTE表明:中部有一定内凹的高阶TE可以降低LTE幅值，载荷较小时，其波形接近几何传动误差（见图4（d）），该工况下LTE最小为0.56″.当高阶TE其他参数不变，内凹程度σ分别取不同的值，LTE幅值（见图4（e））表明:有一定内凹的几何传动误差，可使齿面变‘软’，降低了LTE幅值，该结果与文献［6］一致，即:二次抛物形的传动误差曲线尖顶被磨去，变得与内凹的四次抛物线类似，曲线转换点的夹角几乎成180°，因此可减小轮齿的振动；当σ为-1.5″，载荷为2 000 N·m时，LTE幅值小；当σ为-4.5″、6.0″，载荷大于2 500 N·m时，LTE幅值将达到最小.总之，内凹量大小与齿轮副工况有关，随载荷增加，最佳内凹量呈增大趋势.由于啮入啮出端避免了边缘接触，且有较大的几何传动误差，因此啮合冲击将大大减小，有利于减震.

3.2 CNC加工误差分析

1）经PSO优化后的解在150代基本趋于稳定（见图4（f）），磨削后的修形曲面较为光滑（见图4（g）），磨削误差（未磨削到）≤8μm，主要集中在啮入、啮出端的对角区域.齿面其余部分误差为≤2μm（见图4（h）），还需要用平面砂轮进行对角修形磨齿，磨削后误差≤2μm；因此整个齿面误差将可控制在≤2μm，关于对角修形数控磨齿加工鉴于篇幅文中不做介绍.

2）优化求解的砂轮轴向廓形法向修形曲线（见图4（i1），（i2）），将其与理论齿面叠加，通过B样条拟合可得到砂轮修形齿面的轴向廓型曲线.

3）各轴运动曲线接近直线（见图4（j）），便于数控编程，与磨削理论齿面相比，各轴运动变化（见图4（k））:ΔCx，ΔCy无变化，即无校正；ΔCz接近常数，表明主要进行了齿厚修形；ΔCa变化趋势与图4（b）螺旋角的变化一致（ΔCa=-Δβ），进行了一定齿廓修形；ΔCb变化趋势表明，进行了齿向校正．

4）表3为修形前后各轴运动及砂轮廓形曲线，其中0阶或1阶系数有微小变化；文中关于CNC机床各轴0阶与1阶参数对磨削误差分析结果与文献［11］做了对比分析，部分一致.

表3 五轴CNC斜齿轮成形砂轮磨齿机各轴运动关系及砂轮廓形校正表达式

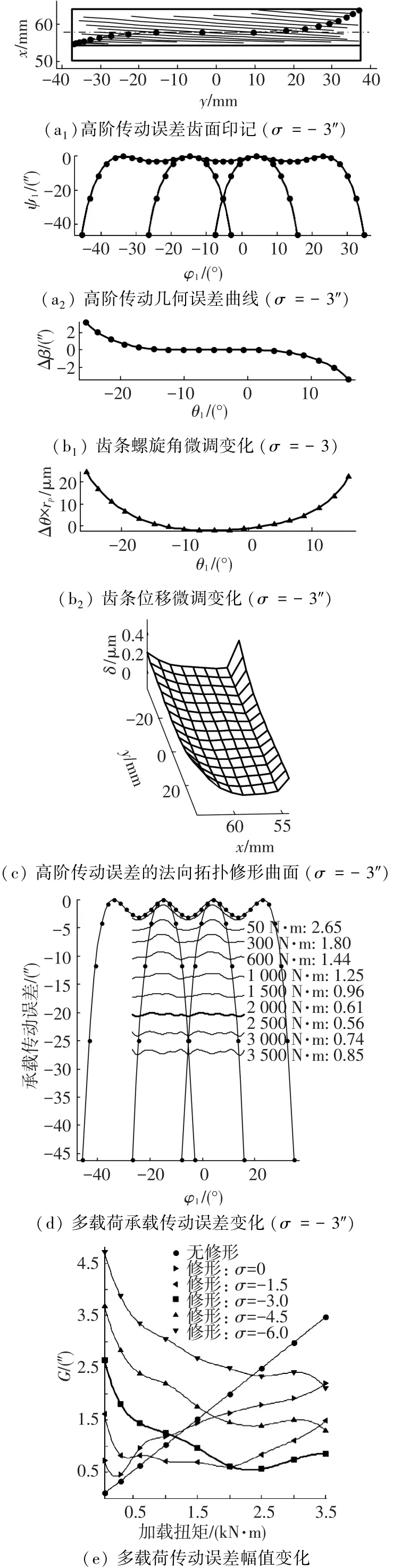
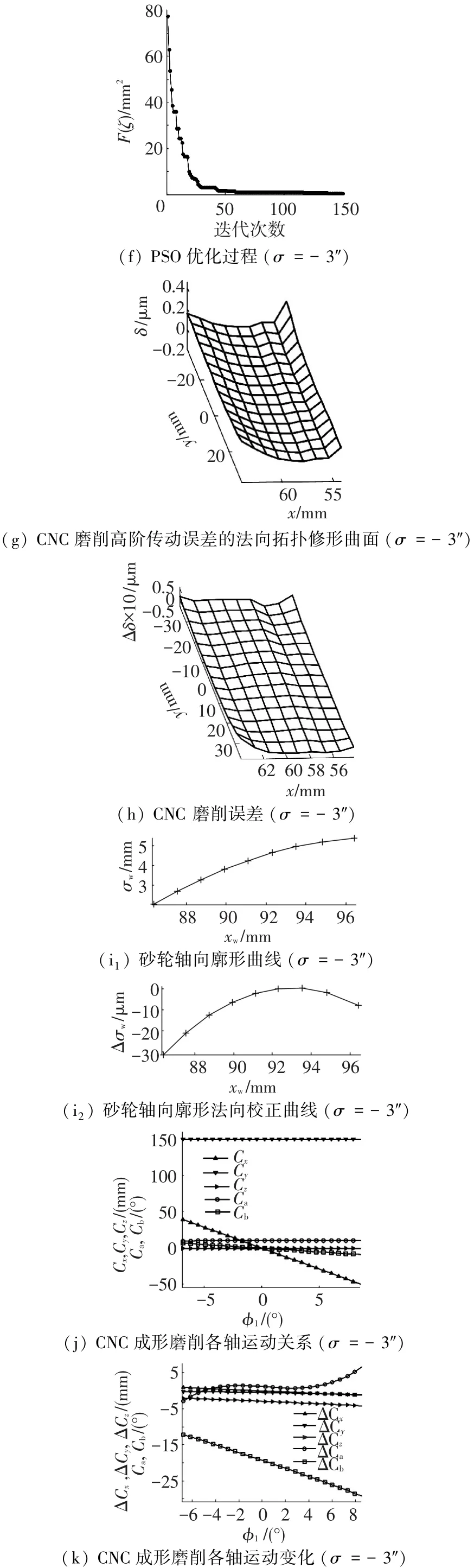
图4 高阶传动误差的斜齿轮修形齿面、传动误差及五轴CNC成形砂轮磨齿各轴运动曲线

4 结 论

1）设计高阶传动误差及齿面接触路径，结合LTCA通过优化承载传动误差幅值最小确定了其参数，根据齿条展成渐开线齿面原理，反求齿条运动参数，计算小轮的法向拓扑修形曲面.

2）建立基于成形砂轮廓形与5轴联动CNC机床各轴运动敏感性分析的成形砂轮磨削斜齿轮5轴联动CNC模型，砂轮廓形的法向修正曲线与各轴运动分别用高阶多项式表示，判断砂轮与齿面的接触状态，确定了磨削齿面的误差，以齿面误差平方和最小为目标函数，通过PSO优化方法，得到机床各轴运动参数及砂轮的轴向廓形的法向修形曲线，该方法计算结果稳定且精度较高.

3）优化的高阶传动误差在曲线转换点处相切连接，修形曲面的特点是啮入端近齿根、啮出端近齿顶处有较大的修形量，修形区域近似对角；有一定微小内凹的高阶传动误差可使齿面变‘软’，降低轮齿的振动，其内凹参数大小与齿轮副工况有关，随载荷增加，最佳内凹量呈增大趋势.

4）高阶传动误差修形齿面，可通过成形砂轮进行主要的修形磨削，然后通过平面砂轮进行辅助的对角修形磨削实现，理论磨削误差＜2μm.

［1］GONZALEZ-PEREZ I，FUENTES A，LITVIN F L. Modified surface topology of involute helical gears developed for improvement of bearing contact and reduction of transmission errors［C］／／International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. California:ASME，2005:571-584.

［2］LITVIN FL，GONZALEZ-PEREZ I，FUENTES A，et al.Design，generation and stress analysis of face gear drive with helical pinion［J］.Computer Methods in Applied Mechanics and Engineering，2005，194: 3870-3901.

［3］MAO K.Gear tooth contact analysis and its application in the reduction of fatiguewear［J］.Wear，2007，262: 1281-1288.

［4］LITVIN F L，FUENTES A.Gear geometry and applied theory（second edition）［M］.New York:Cambridge University Press，2004:240-260.

［5］方宗德.修形斜齿轮承载接触分析［J］.航空动力学报，1997，12（3）:251-254.

［6］STADTFELD H J，GAISER U.The ultimate motion graph［J］.Journal of Mechanical Design，2000，122: 317-322.

［7］樊奇，让·德福·格里森.专家制造系统开创弧齿锥齿轮及双曲面齿轮数字化制造新纪元［J］.产品与技术，2005，8（4）:87-92.

［8］方宗德，刘涛，邓效忠.基于传动误差设计的弧齿锥齿轮啮合分析［J］.航空学报，2002，23（3）: 226-230.

［9］LEE C K.Manufacturing process for a cylindrical crown gear drive with a controllable fourth order polynomial function of transmission error［J］.Journal of Materials Processing Technology，2009，209（1）:3-13.

［10］王小椿，王军，姜虹.螺旋锥齿轮的齿面测量及机床加工参数修正［J］.机械工程学报，2003，39（8）: 125-128.

［11］SHIH Y P，FONG Z H.Free-form flank correction in helical gear grinding using a five-axis computer numerical control gear profile grinding machine［J］. Journal of Manufacturing Science and Engineering，2012，134（4）:041006-1-13.

［12］LIN C Y，TSAY C B，FONG Z H.Computer aided manufacturing of spiral bevel and hypoid gears by applying optimization techniques［J］.Journal of Materials Processing Technology，2001，114（1）: 22-35.

［13］SHIH Y P，FONG ZH.Flank correction for spiralbevel and hypoid gears on a six-axis CNC hypoid gear generator［J］.Journal of Mechanical Design，2008，130（6）:062604-1-11.

［14］FAN Q，DAFOE R S，SWANGER JW.Higher-order tooth flank form error correction for face-milled spiral bevel and hypoid gears［J］.Journal of Mechanical Design，2008，130（7）:072601-1-7.

［15］SIMON V V.Generation of hypoid gears on CNC hypoid generator［J］.Journal of Mechanical Design，2011，133（12）:121003-1-9.

［16］SHIH Y P.Mathematicalmodel for face-hobbed straight bevel gears［J］.Journal of Mechanical Design，2012，134（9）:091006-1-11.

［17］SHIH Y P.A novel ease-off flank modification methodology for spiral bevel and hypoid gears［J］.Mechanism and Machine Theory，2010，45（8）:1108-1124.

［18］ARTONIA，KOLIVANDM，KAHRAMAN A.An easeoffbased optimization of the loaded transmission error of hypoid gears［J］.Journal of Mechanical Design，2010，132（1）:011010-1-9.

［19］王立鼎，凌四营，马勇.精密、超精密圆柱渐开线齿轮的加工方法［J］.光学精密工程，2009，17（2）: 322-325.

［20］史峰，王辉，郁磊，等.Matlab智能算法30个案例分析［M］.北京:北京航空航天大学出版社，2007: 55-60.

（编辑杨 波）

Design and grinding for modified helical gears w ith a higher-order transm ission error

JIANG Jinke，FANG Zongde，SU Jinzhan
（School of Mechanical Engineering，Northwestern Polytechnical University，710072 Xi’an，China）

An approach was proposed to reduce grinding errors and improve meshing performance.Firstly，both a controllable contact path and a high order transmission error（H-TE）curveswere designed based on the TCA theory，and the parameters of curves were got by optimizing the minimum amplitude of LTE based on LTCA，and topologicallymodified tooth of pinion was determined according tomovementof the rack generating involute tooth.Secondly，a free-form CNC grindingmachinemodel of five-axis was established and kinematic relationships of the axeswere derived.Besides，an error correctionmodel based on a sensitivity analysis of the grindingwheel and themovementof five-axiswas determined，and grinding errorwas established by estimating whether the wheel contact with the pinion，and the corrections were solved by using the PSO optimization algorithm.Finally，an example shows that the optimized higher-order transmission error curves is smooth at the intersect points，and topologicallymodified tooth is characteristics ofmoremodification and proximal diagonal at engaging-in and engaging-out regions.Besides，a middle concave higher-order transmission error curve makes a smaller LTE amplitude，which helps to reduce vibration；Further more，the parameters of concave depends on working condition，and with the increasing of loads，the optimal parameters value increases.The modified tooth can be efficiently ground by slightly adjusting five-axis movement and the wheel profile according to the solved corrections and then by flat grinding wheel for diagonal correction，which effectively reduce the grinding errors to 2μm.

helical gear；topologicallymodified；higher-order transmission error；CNC grinding；formingwheel

V219

A

0367-6234（2014）09-0043-07

2013-09-12.

国家自然科学基金资助项目（51175423，51375384）.

蒋进科（1981—），男，博士研究生；方宗德（1948—），男，教授，博士生导师.

方宗德，fauto＠nwpu.edu.cn.