Myring型回转体直航阻力计算及艇型优化

庞永杰，王亚兴，杨卓懿，高 婷

（哈尔滨工程大学水下智能机器人技术重点实验室，黑龙江哈尔滨150001）

Myring型回转体直航阻力计算及艇型优化

庞永杰，王亚兴，杨卓懿，高 婷

（哈尔滨工程大学水下智能机器人技术重点实验室，黑龙江哈尔滨150001）

在水下智能机器人（AUV）方案设计阶段，针对如何在主尺度和巡航速度确定的前提下得到直航阻力最小的回转体形状这个问题，以Myring型回转体为研究对象，利用计算流体力学（CFD）方法计算其在水中做匀速直航运动时的阻力并与试验值比较以验证准确性。分别对二维和三维2种网格形式，标准和加强2种壁面函数的计算精度和计算效率进行了对比，并在此基础上探讨单独改变艏部或艉部形状时阻力的变化规律。再利用EXCEL、ICEM、FLUENT建立优化平台，基于多岛遗传算法在限制条件范围内对Myring型回转体参数进行全局寻优，寻找不同流速时阻力最小的Myring型回转体，为AUV设计阶段的阻力性能预报和艇型优化提供参考。

水下智能机器人；回转体；阻力；模型试验；多岛遗传算法；流体力学；网格生成；壁面函数

水下智能机器人（autonomous underwater vehicles，AUV）作为完成多种水下任务的重要工具，无论在军事还是科研领域都有广阔的前景。足够的续航力和巡航速度是AUV完成预定任务的前提。目前AUV不能达到预定续航力和速度的原因主要是低估了AUV的航行阻力或AUV本身直航阻力过大。本文通过经验公式，计算流体力学方法（CFD）对AUV航行中所受的阻力进行预估并参考实验数据进行验证，寻找满足预定设计要求且能够有效降低直航阻力的Myring型回转体解决方案。

1 概述

1.1 Myring型回转体

回转体AUV的艇型一般由公式给出艏艉形状曲线，并根据需要决定是否使用平行中段，常用的艏艉形状有 Myring型［1］、Nystrom 型［2］、卡克斯型［2］、水滴型［3］等，邱辽原［4］在潜艇粘性流场数值模拟研究中也提出了一种艇型。这些艇型都可以通过改变公式中的参数值来获得不同的形状。所有回转体形式中Myring型使用得较多，著名AUV如Remus，MAYA都使用此形式，本文对Myring型回转体进行系统分析，寻找以Myring方程为基础的回转体直航阻力的确定方法，为AUV设计中预估艇体阻力和有效降低总阻力提供参考。Myring给出的艏部形状方程为

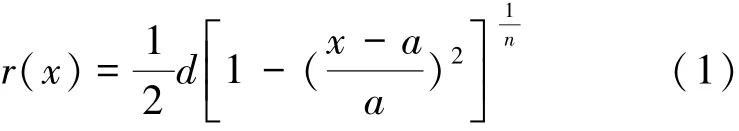
艉部形状方程为

式中：a为艏部长度，b为平行中体长度，c为艉部长度，d为中体直径，x是长轴上点到艏部顶点的距离，r为x点处的半径，n和θ分别是控制艏艉曲线饱和程度的参数。n和θ越大艏艉越饱满。图1给出了a＝25，b＝15，c＝30，d＝10的时候不同n和θ值下艏艉的形状。

图1 不同n值和θ值时Myring方程给出的艏艉形状Fig.1 Structure diagram of inductive energy storage shape of revolution body when different n and θ are adopted

1.2 回转体阻力计算

获得回转体直航阻力的方法主要有经验公式、CFD方法和模型试验。Barros将计算导弹和鱼雷航行阻力的DATCOM方法借鉴到AUV艇体阻力计算中［5］，Prestero在计算Remus艇体阻力［6］时引用了Triantafyllou的成果。经验公式最大的优点就是计算迅速，但是计算精度不够，只能在设计初期为设计者提供一定的参考。随着计算机技术的飞速发展，CFD方法计算AUV水动力性能也得到大范围的应用，受计算机水平的影响，直接数值模拟（DNS）和大涡模拟（LES）尚处于发展阶段，利用时均化的方法求解Navier-Stokes方程（RANS）已经广泛应用于计算流体力学领域，并发展出多种湍流模型。CFD方法较经验公式求解更为准确，耗费的时间也相对长一些，但与模型试验相比耗时要短很多，且成本也远小于后者。模型试验是获得AUV水动力参数最直接有效的方法，但成本也最高，而且受试验设备精度和尺度效应影响，仍会存在误差。

2 CFD计算和模型试验

2.1 CFD计算

CFD计算回转体直航阻力有三维和二维2种计算方法。前者直接模拟真实的三维空间流场环境，利用体网格求解三维空间下的N-S方程并对回转体表面积分得到阻力值，后者则使用面网格，将回转体的对称轴作为旋转轴边界条件，直接求解二维空间上的N-S方程，解得回转体表面沿长度方向上的压力分布，利用回转体的轴对称性求解阻力，这种方法的原理可以参考OpenFoam关于楔形体计算的相关理论［7］。

二维和三维结构化网格见图2。通过计算验证二维和三维模型CFD计算之间的误差不超过2%。

图2 二维和三维结构化网格Fig.2 3D and 2D structured mesh

对流场采用有限体积法求解RANS方程，湍流模型选择在近壁区算法更稳定且精度更好的剪切应力输运k-ω模型［8］，即SST k-ω模型。为使计算更加准确，收敛更快，使用结构化网格对流场进行划分，为避免流域边界对流场产生影响，流场应足够大，整个外域采用圆柱体。根据Barros的建议，流场的总长度取艇长的15倍，直径为艇体直径的25倍［9］。虽然SST k-ω模型在近壁区的计算上有优势，但仍需借助壁面函数法将壁面上的物理量与湍流核心区内的物理量联系起来。不同的壁面函数对第一层网格高度的无量纲参数y＋要求不同，y＋的表达式为

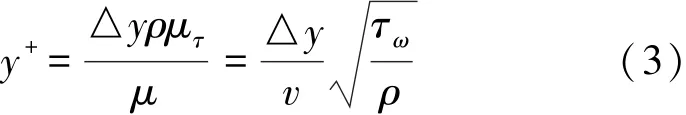
式中：△y是第一层网格高度，μτ是壁面摩擦速度，ρ是水的密度，τω为壁面切应力，

标准壁面函数［10］要求y＋值应尽量满足30 ＜y＋＜60。如果采用加强壁面函数［11］，则应尽量满足y＋＝1，最大不能超过5。表1给出了选择不同的y＋时得到的阻力值。此时来流速度为1.5 m／s。试验值为9.79 N。

表1 y＋值对模型阻力计算的影响Table 1 Effect of y＋to model drag calculation

虽然使用标准壁面函数较加强壁面函数误差偏大，但仍不超过2%。考虑到后续的优化工作需要进行大量的重复计算，本文仍然选择标准壁面函数。

2.2 模型试验

为获得不同长度艏艉配合的回转体阻力性能，设计并制作一组玻璃钢模型，包括可拆卸的艏部与艉部各两个以及一个平行中段。模型中段直径d＝280 mm，长度b＝734 mm。两组艏部参数分别为a＝280 mm，n＝2和a＝504，n＝1.8；两组艉部参数分别为c＝504，θ＝38°和c＝784，θ＝27°。两组艏和两组艉与平行中段分别进行组合，组合形式如图3，从上到下依次为组合1到组合4。

图3 模型试验4种组合形式Fig.3 4 types of model assembly

将4种组合分别在水平型循环水槽中进行试验，改变来流速度，利用六分力天平测量各种组合的受力情况，并提取其中的轴向力进行比较。试验模型见图4。图5显示的是组合1在循环水槽中进行试验。试验中测力天平布置在回转体内部轴线上，利用两个剑杆固定测力天平和回转体模型，为将剑杆对回转体周围流场的影响降到最小，剑杆底部的直径仅为10 mm，约为模型尺度的5%，而且本试验中回转体不运动，故剑杆对回转体的轴向上的受力影响很小。

图4 试验模型Fig.4 Test model

图5 组合1在进行试验Fig.5 Assembly 1 is carrying out experiment

2.3 结果对比

图6给出组合1和组合4通过CFD计算和模型试验EXP获得的回转体阻力值，组合2和组合3结果相同。CFD计算与模型试验获得D的阻力值基本一致，但在来流速度过高时模型试验值明显高于CFD计算值，这主要是因为循环水槽造流能力的限制，生成流速大于1.5 m／s时伴随产生过高的湍流，流场不稳定使阻力增加。

图6 组合1和组合4阻力曲线Fig.6 Drag curves of assembly 1 and 4

3 利用CFD计算优化艇型

要利用CFD方法进行艇型优化需要不断改变艇型参数，建立模型并划分网格，再利用CFD程序迭代求解RANS方程获得阻力值。三维模型进行一次CFD计算约需要60～80万体网格，利用4个CPU来迭代2 h以上才可能收敛得到阻力值，二维模型一次CFD计算则仅需9～12万面网格，用一个CPU经过5 min的计算即可得到阻力值。以1 000次计算为例，前者需要80 d，后者则仅需4 d，但两者计算结果相差并不大。本文利用二维模型进行艇型优化。

3.1 艏部和艉部的优化

虽然对于回转体来说中段的长度越小对减小阻力越有利，但AUV的设计中考虑到总体布置需要，有时会确定平行中段的长度b，再考虑改变艏部和艉部形状以达到减小直航阻力的目的。即在b和d都固定的前提下讨论a和n（或b和θ）变化对直航阻力的影响。本文取试验参数作为建模参考，即b＝734 mm，d＝280 mm，由于本试验的目的是为AUV的实际设计提供依据，取来流速度为AUV的预定巡航速度3 kn（1.5 m／s）。

图7（a）给出c＝784 mm，θ＝27°固定不变，a＝d、2d、3d、4d时n从0.3增加到4.9过程中CFD计算模型阻力值的变化。从中可以看出在计算范围内不论n取何值，总阻力都随a值的增大而增加，除a＝d时n值的增加对总阻力的影响不大外，在其他情况下n值的增加都会使总阻力增加，且在n＜2时阻力的增加量特别明显。这一结论和Myring的结论［1］有一定的差别，主要是因为Myring的试验是在Re＝107的条件下进行的，而本试验Re＝3×106，此时摩擦阻力在总阻力中的比例较大，而a越大，湿表面积越大，致使摩擦阻力变大。因而Myring的试验结论［1］直接运用于航速较低的AUV艇型优化具有局限性。

图7（b）给出a＝504 mm，n＝1.8保持不变，c＝2d、3d、4d、5d时θ从1°增加到35°过程中CFD计算模型阻力的变化。c＝2d时的阻力θ的增加对总阻力几乎没有影响，越大的c值的总阻力随θ变化幅度越大。

图7 阻力随a和n，c和θ变化曲线Fig.7 Drag curves of n when different a is adopted，c when different θ is adopted

3.2 固定总容积的艇型优化

3.2.1 计算模型

AUV设计中可能根据任务需求和设备大小情况先确定需要的总容积，并给出艇体总长度和直径的比值所存在的范围。针对AUV直航阻力的艇型优化也假定回转体的体积和细长比已经确定，利用Myring方程定义回转体曲线寻找阻力最优解，即在V和d／l范围已知的前提下考查a、b、c、n和θ不停变化时直航阻力的变化。为与试验数据进行对比，并考虑为水下航行器的设计提供参考，取l＜10d，0.09 m3＜V＜0.15 m3对，Myring型回转体进行优化。

利用优化程序集成EXCEL、ICEM和FLUENT，集成原理图见图8，首先由优化组件提供a、b、c、n和θ的初始值，利用计算器作为条件限制组件保证输出值的正确性，再用内置在EXCEL中的VBA程序读入初始值并输出型值文件，ICEM执行RPL文件利用型值构建二维计算模型并输出非结构网格文件，FLUENT执行JOU文件导入网格进行迭代，迭代初步稳定后据AUV的边界层y＋值和流场的速度梯度对网格进行自适应后再计算，自适应前后网格的变化见图9，待迭代稳定后提取阻力值。优化组件根据求得的阻力值重新生成a、b、c、n和θ并重复上述步骤，直到寻找到最优解。优化过程中使用非结构网格而不是结构网格主要是因为非结构网格能更好的适应AUV型线的不断变化，而且初步计算后自适应新增的加密网格本身也是非结构的。本算例的几何结构非常简单，所以非结构网格计算结果与结构网格计算结果几乎完全相同。只是在收敛速度方面前者比较差，故在优化过程中增加了FLUENT迭代的次数。优化中来流速度分别取v＝0.5、1.0、1.5、2.0 m／s。

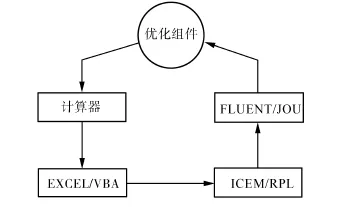
图8 优化过程Fig.8 Optimizing process

图9 自适应前后网格Fig.9 Mesh before and after self-adaption

优化中改变各参数但保证a＞200 mm，b＞50 mm，c＞100 mm，d＞100 mm，0.6＜n＜3，5°＜θ＜35°不断变换参数值并提取迭代计算获得的阻力值。为达到寻找最优解并避免得到局部最优解的目的，优化方法选择全局探索方法中的多岛遗传算法［12］（multi-island and genetic algorithm，MIGA）优化二维模型。为保证寻优过程的有效性并充分利用计算机资源，本文MIGA的种群规模取30，进化代数20，交叉概率取1，变异概率0.01，迁移概率0.1，每次计算用时6 min，在每一个来流速度下共计算2 000次。

3.2.2 优化结果

图10是来流速度为v＝0.5 m／s时利用多岛遗传算法，以阻力值最小和体积值最大同时作为优化目标得到的计算结果，从结果看在某一体积值下，无论回转体的形状如何变化，都不会小于某一阻力值Dmin，且 Dmin值随体积的增加近似呈线性规律增加。图 11显示的是来流速度分别为0.5、1.0、1.5、2.0 m／s时Dmin随体积增加的变化规律。虽然速度越大Dmin随体积变化的越快，但在这几个来流速度下的阻力最优艇型基本上都如图12所示。平行中段很小甚至没有，艏部长度和艉部长度的比值a／c约为4，总长度与直径的比值l／d约为8，n不超过2.5，θ不超过30°。

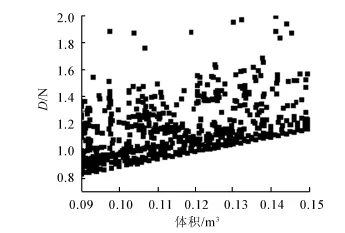
图10 v＝0.5 m／s时随体积增加回转体阻力计算结果Fig.10 Drag of different volumes when v＝0.5 m／s

图11 不同速度下最小艇体阻力随体积变化图Fig.11 Minimal drag curves at different speeds

图12 阻力最优艇型Fig.12 Best revolution body shape with minimal drag

4 结束语

本文以Myring型回转体为研究对象，利用CFD方法研究了改变回转体艏或艉的长度和饱满程度时对回转体直航阻力的影响。搭建了一个优化平台，在固定艇体总容积的前提下利用多岛遗传算法寻找改变回转体艏、中、艉3部分在总长度中的比例以及外形参数时阻力最优的方案，同时得到了一种阻力最优艇型。对水下航行器的设计工作具有很好的参考价值。

［1］MYRING D F.A theoretical study of body drag in subcritical axisymmetric flow［J］.Aeronautical Quarterly，1976，27（3）：186-194.

［2］杜月中，闵健，郭字洲.流线型回转体外形设计综述与线型拟合［J］.声学技术，2004，23（2）：93-101.

DU Yuezhong，MIN Jian，GUO Zizhou.A review and mathematical formulation of shape design of streamlined bodies of revolution［J］.Technical Acoustics，2004，23（2）：93-101.

［3］吴宝山，潘子英，夏贤，等.水滴型回转体带尾导管的水动力特性研究［J］.船舶力学，2003（6）：54-59.

WU Baoshan，PAN Ziying，XIA Xian，et al.Investigation of the hydrodynamic characteristics of body of revolution with stern ring-wing［J］.Journal of Ship Mechanics，2003（6）：54-59.

［4］邱辽原.潜艇粘性流场的数值模拟及其阻力预报的方法研究［D］.武汉：华中科技大学，2006：79-84.

QIU Liaoyuan.Numerical simulation of the viscous flow over the submarine and method research on predicting its viscous resistance［D］.Wuhan：Huazhong University of Science and Technology，2006：79-84.

［5］De BARROS E A，PASCOAL A，De SA E.Investigation of a method for predicting AUV derivatives［J］.Ocean Engineering，2008，35：1627-1636.

［6］PRESTERO T.Verification of a six-degree of freedom simulation model for the REMUS autonomous underwater vehicle［D］.California：University of California，1994：25-27.

［7］Open Foam user guide，version 2.1.1［EB／OL］.（2012-12-05）.http：／／www.openfoam.com.

［8］王福军.计算流体动力学分析［M］.北京：清华大学出版社，2004：202-204.

［9］De BARROS E A，DANTAS J L D.Effect of a propeller duct on AUV maneuverability［J］.Ocean Engineering，2012，42：61-70.

［10］SALIM M S，CHEAH S C.Wall y＋strategy for dealing with wall-bounded turbulent flows［C］／／Proceedings of the International Multiconference of Engineers and Computer Scientists.Hong Kong，2009（2）：2165-2170.

［11］MULVANY N J，CHEN Li，TU Jiyuan，et al.Steady-state evaluation of two equation rans turbulence models for high-Reynolds number hydrodynamic flow simulations［R］.Victoria：DSTO Platform Sciences Laboratory，2004：14-15.

［12］钟毅芳，陈柏鸿，王周宏.多学科综合优化设计原理与方法［M］.武汉：华中科技大学出版社，2007：64-68.

Direct route drag calculation and shape optimization of Myring shape axisymmetric revolution body

PANG Yongjie，WANG Yaxing，YANG Zhuoyi，GAO Ting
（State Key Laboratory of Science and Technology on Autonomous Underwater Vehicle，Harbin Engineering University，Harbin 150001，China）

When main dimensions and cruising speed have been predefined，how to get an axisymmetric revolution body with minimal drag force at the conceptual design stage of autonomous underwater vehicles（AUVs）has been a problem.This paper analyzed drag force of Myring shaped axisymmetric revolution body moving underwater in a direct route，at constant speed，by CFD method and compared with the experiment value to check the veracity.2D or 3D mesh，standard or enhanced wall treatment function was adopted respectively to figure out the accuracy and efficiency.And on this basis，the change law of drag when changing merely length and shape of the nose or tail was discussed.Based on multi-island and genetic algorithm （MIGA），an optimization platform was constructed with EXCEL，ICEM and FLUENT to search for the best axisymmetric revolution body with minimal drag force at different speed when volume is predefined.This is a good reference for calculating and minimizing total drag of AUVs.

autonomous underwater vehicles（AUV）；revolution body；drag；model test；multi-island and genetic algorithm（MIGA）；fluid dynamics；mesh generation；wall function

10.3969／j.issn.1006-7043.201304028

U674.941

A

1006-7043（2014）09-1093-06

http：／／www.cnki.net／kcms／doi／10.3969／j.issn.1006-7043.201304028.html

2013-04-08. 网络出版时间：2014-08-29.

国防科学工业委员会基础研究基金资助项目（9140C270305120 C2701，A2420110001）.

庞永杰（1955-），男，教授，博士生导师.

庞永杰，E-mail：pangyongjie＠hrbeu.edu.cn.