液舱晃荡与船体非线性时域耦合运动计算

黄 硕，段文洋，游亚戈，姜金辉，王文胜

（1.中国科学院可再生能源重点实验室，广东广州510000；2.中国科学院广州能源研究所，广东广州510000；3.哈尔滨工程大学船舶工程学院，黑龙江哈尔滨150001；4.上海船舶运输科学研究所，上海200135）

液舱晃荡与船体非线性时域耦合运动计算

黄 硕1，2，3，段文洋3，游亚戈1，2，姜金辉4，王文胜1，2

（1.中国科学院可再生能源重点实验室，广东广州510000；2.中国科学院广州能源研究所，广东广州510000；3.哈尔滨工程大学船舶工程学院，黑龙江哈尔滨150001；4.上海船舶运输科学研究所，上海200135）

LNG船等液货船的研制和应用中，为了研究非线性水动力对液舱晃荡及船体运动的影响，改进了规则波及不规则波中液舱晃荡与船体非线性耦合运动的时域预报技术。通过改变液舱物面边界条件模拟能量耗散，对液舱内部流动采用全非线性模型，船体外流场采用非线性瞬时物面条件的时域格林函数边界元模型，并应用基于组合B样条的高阶面元法求解边值问题和迭代半隐式时域步进法对内外流场和船体运动同时求解。通过对比，验证了这种考虑能量耗散的方法的有效性，研究了非线性水动力中各种因素的影响，得出能量耗散系数μ的选取规律。

液舱晃荡；能量耗散；全非线性模型；时域耦合运动；LNG船；B样条；迭代半隐式时域步进法

液舱部分装载时舱内液体大幅晃荡可能会给船体带来巨大的危害。因此在时域内直接求解液舱晃荡与船体非线性耦合运动问题具有很大的吸引力。目前国内外学者就该问题分别应用线性频域及非线性理论对液舱晃荡进行模拟［1-2］，对船体运动大多采用线性方法进行分析［3-4］。但试验发现即使入射波是微幅线性的，某些频率下巨大的晃荡冲击压力会导致船体运动平衡位置及湿表面的大幅变化，作用在船体上的流体动力载荷具有明显的非线性特点。

为求解这种耦合问题，首先要对液舱晃荡问题进行精确高效的计算。部分学者应用Navier-Stokes方程进行求解［5］。但其计算时间较长，所以应用加入人工能量耗散［6］的势流理论。文献［7-8］建立了一种改进的物面边界条件模拟能量耗散，但只对线性液藏晃荡问题进行了研究。

鉴于上述问题，首先将文献［8］建立的能量耗散条件扩展到全非线性液舱晃荡数值模拟中。注意到即使入射波是线性的，船体摇荡引起舱液晃荡的非线性也非常显著。因此，抓住该耦合问题的主要矛盾，对船体外部流动采用线性自由面和非线性瞬时物面条件的时域分析方法，对液舱内部流动采用改进的全非线性模型，利用B样条高阶面元法对边界积分方程进行离散［9］。扩展文献［10］提出的迭代半隐式时域步进法（ISITIMFB）对内外流场和船体运动同时求解。在规则波及不规则波作用下对液舱晃荡与船体非线性耦合运动进行计算，通过与文献［11-12］中频域及试验结果的对比，研究能量耗散条件的作用效果，得到能量耗散系数μ的选取规律。

1 数学模型

1.1 全非线性液舱晃荡

1.1.1 速度势定解条件

为方便求解，对全非线性液舱晃荡的模拟在动坐标系oTyTzT下进行，如图1。其与大地坐标系OYZ关系为

式中：α为欧拉角，T为转化矩阵。

图1 液舱坐标系Fig.1 Coordinate system of the tank

假定流体为不可压缩无粘无旋，在计算域SΩ内速度势φ满足的定解条件［13］为

式中：ζb是oTyTzT下的自由表面波高，V和W是速度U在oTyT和oTzT方向的分量，单位法向量n指向流体域外部，g是重力加速度，Tij是T中的系数，SB（t）是液舱瞬时湿表面。

采用简单格林函数法，将问题转化为

式中：C为P点处流场边界的两条半切线之间的夹角在域内的部分，S为除去P点的整个流域边界。

值得注意的是，速度势定解问题是在动坐标系下求解，因此流体对舱壁压力可写为

1.1.2 能量耗散的近似

为了在势流理论模型式（2）中引入粘性效应，文献［7］在频域分析中认为能量耗散主要发生在壁面边界层处，因此对液舱物面边界条件进行改进。文献［8］首先将该方法应用到时域计算中，得到直接的时域表达形式为

式中：μ是阻尼系数，SB是液舱平均湿表面。Un反映能量耗散，是与式（2）中相同的物面法向速度。

数值研究发现式（5）中的系数μ依赖于液舱形状及充液比例。这需要针对不同的工况选择不同的系数μ，在实际应用中是相对困难的。为了避免式（5）带来的问题，文献［8］将式（5）改进为

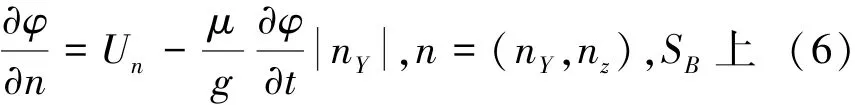
在全非线性液舱晃荡数值模拟中，注意到物面条件在瞬时湿表面SB（t）上满足，并将式（1）代入式（6）得到改进物面条件在动作标系oTyTzT下的表达式：

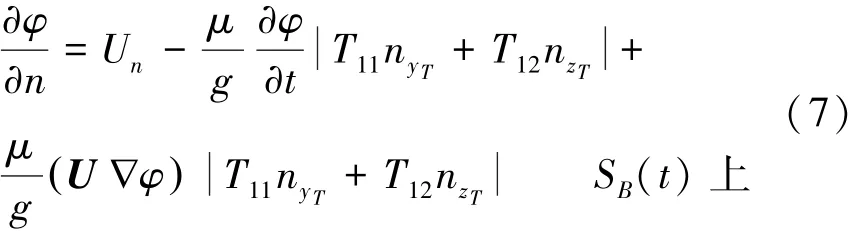
1.1.3 动坐标系下∂φ／∂t的定解条件

为解决∂φ／∂t的计算难题，仿照速度势φ的求解过程，把∂φ／∂t看成一个调和函数，建立了∂φ／∂t的在大地坐标系OYZ下的定解条件［15］：

由于求解是建立在液舱动坐标系oTyTzT下，因此需建立动坐标系下∂φ／∂t的定解条件，得

动坐标系下∂φ／∂t的自由面条件已由式（2）给出，至此建立了动坐标系下∂φ／∂t的定解条件。

1.2 液舱晃荡与船体非线性耦合运动

考虑任意形状带有液舱的船体在自由水表面作大幅摇荡的运动问题，定义3个坐标系如图2。

1）大地坐标系OYZ，表述入射波及船体周围的扰动流场，建立船体的运动方程。

2）船体动坐标系oyz。表述船体表面，其随船体一起平移和旋转。t＝0时刻，o与O重合。摇荡时，船体重心G′的位置矢量为S＝（η1，η2，η3）。

3）液舱局部动坐标系oTyTzT。t＝0时刻，oTyT轴与液舱静水面重合，oTzT轴通过船体的重心G，且oT在液舱内部水线面中心处。

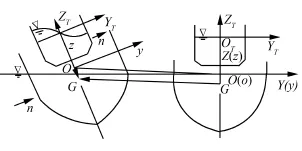
图2 坐标系的建立Fig.2 Coordinate definition

未扰动时，以上3个坐标系互相平行，流场边界上的单位法向量均指向流体域外部。

理想流体假设下，存在 φ ＝φ0＋φp。 其中，φ0为入射势，φp为扰动势。入射波的一阶速度势为

式中：ζa是入射波波幅，ω是入射波频率，k0是波数。

扰动势φp的物面非线性定解条件写为

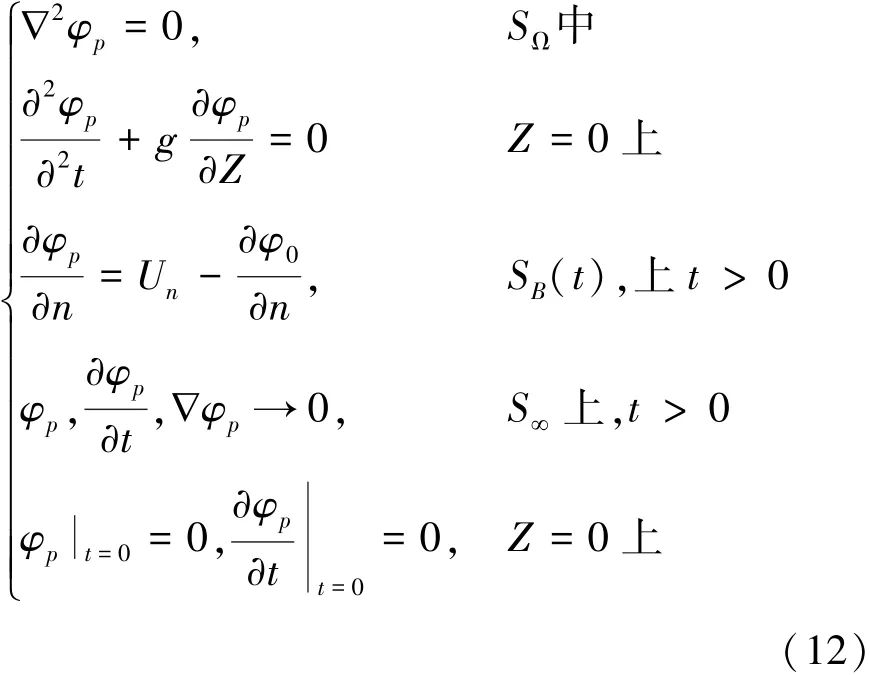
满足线性自由面条件的时域Green函数为

式中：δ（t）为 delta函数，H t()为单位阶跃函数，τ≤t。

求解扰动势φp的物面非线性分布源模型［16］为

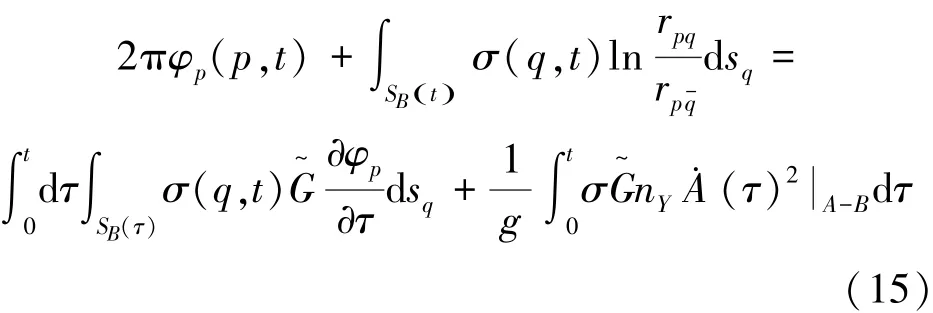
式中：B（t）和A（t）为浮体与自由面Z＝0左右两交点的横坐标，和为点B和A的横坐标对时间导数，｜A－B表示两交点对应的值相减。

液舱剧烈晃荡与船体非线性耦合运动需在船体重心处建立运动方程：

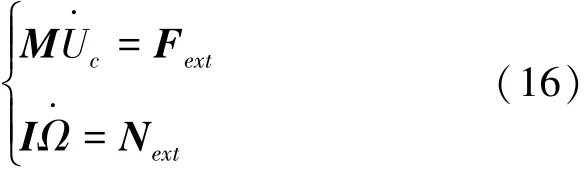
式中：除了有外流场水动力（矩）F（N），横向弹簧回复力Kη2，阻尼力，船体重力及横摇阻尼力矩Nc外，还有液舱晃荡水动力（矩）Fsloshing（Nsloshing）的作用；K为弹簧刚度系数；C为阻尼系数；m为裸船质量。本文应用文献［11］的一种半解析的方法估算非线性横摇阻尼力矩：

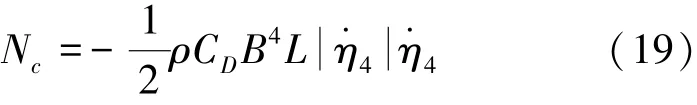
式中：CD为无量纲的阻尼系数，B为船宽，L为船长。

为避免每一时间步逐点对时间微分，再对∂φ／∂t积分导致的时域模拟失效。采用文献［16］提出的先积分后微分的船体大幅运动水动力计算公式：

由于在耦合运动计算中船体运动需时时传递至液舱，同时液舱的晃荡力（矩）亦需时时作用于船体，故还需对这2组物理量在不同坐标系下转换。

2 数值模拟方法

2.1 基于组合B样条的高阶面元法

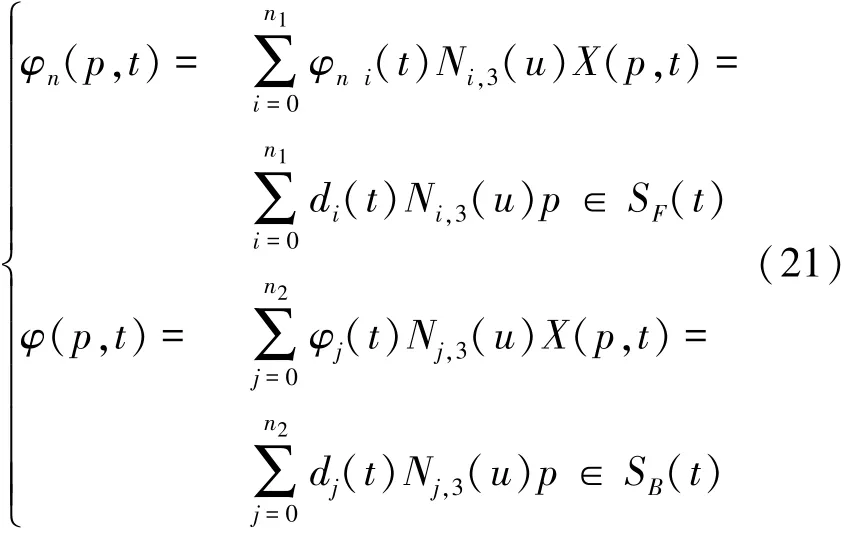
对于如式（2）描述的定解问题的求解，本文发展了一种基于B样条的高阶面元法。未知的速度势φ和物体几何形状可由3次B样条曲线定义：式中：di（t）和dj（t）分别是自由面和瞬时物面上的控制点，n1和 n2是相应的控制点数目，φni（t）和φj（t）是相应控制点上的速度势法向导数和速度势。

在自由面和物面交点 P处采用重节点技术。应用B样条端点条件，交点处边界及连续性条件为

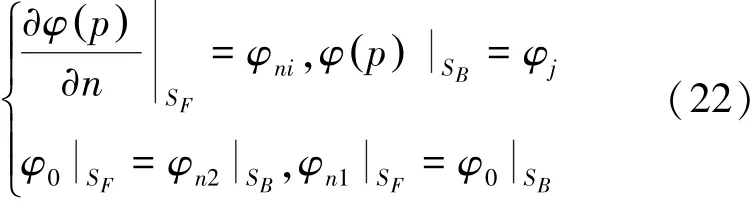
将式（22）代入式（3）可得到以自由面及物面上诸控制点di（t）和dj（t）对应的φj（t）和φnj（t）为未知数的线性方程，求解过程参见文献［17］。

2.2 运动方程解耦

本文对ISITIMFB方法［18］进行扩展，在每一时间步，船体运动时时传递给液舱，求解该时刻液舱内部流场，再对舱壁上的压力积分计算出液舱的晃荡力添加至船体运动方程，进而对耦合运动解耦。

首先假定在t＝tn－1时刻，所有计算都已完成。tn时刻的船体及流体速度可按如下得到：

1）基于最小二乘法，由前面诸时刻已知的加速度预估tn时刻的船体加速度和液舱晃荡能量耗散条件中的 (∂φT／∂t )n（0），应用Adams-Moulton方法［19］预估船体速度Un（0）：

2）将当前预估的Un（0）及 （∂φT／∂t）n（0）代入液舱和船体水动力定解条件中求解φp和φT。

3）计算液舱内部流体自由面表面速度势及流体速度，速度由当前的Un（0）转换得到。

4）求解船体的受力及加速度：

①应用U·n（k－1）和 Un（k－1）求解舱内物面及自由面上的 ，n（k－1）表示t时刻的第k次n迭代；

②计算船体受力Fn（k），船体加速度及速度为

Mb是裸船惯性矩阵，

③应用Un（k）求解船体及液舱物面速度势；

④判断船体加速度的相对误差e，如误差足够小，继续第5）步计算，否则重复第4）步。

5）应用上步最后迭代得到的 Un（u）和 U·n（u）步进船体位移，tn＋1时刻船体位移以三阶泰勒展开：

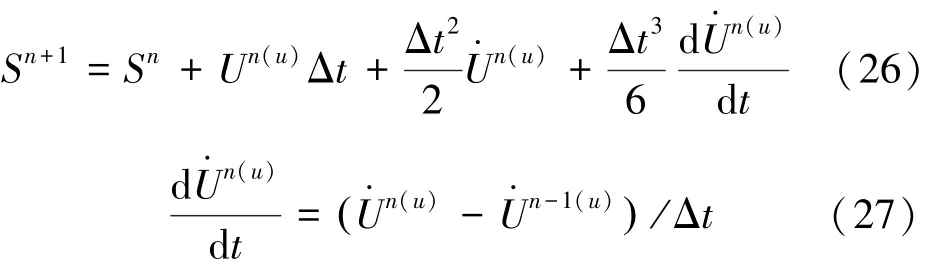
应用最后计算的液舱内部流体自由表面速度势计算液舱内部流体自由表面速度。步进下一时刻tn＋1液舱内部自由表面上∂φ／∂t、自由表面、瞬时湿表面及船体瞬时湿表面位置。

3 时域数值计算及试验验证

3.1 新阻尼模型的效率

能量耗散条件提出的主要目的是在液舱晃荡与船体耦合运动的求解中应用势流理论对晃荡产生的水动力进行符合实际的模拟。关键部分就是能量耗散系数μ的选取。为研究其在长时间数值模拟中的作用，对文献［1］试验中带液舱驳船横荡运动（如图3）进行模拟。为充分反映晃荡特性，数值计算时长都选入射波周期的60倍，对μ取0.0、0.3、0.5、0.7、0.9、1.1。典型激励频率下液舱晃荡与驳船横荡耦合运动时历如图4所示。对时历曲线稳态段做快速傅里叶变换得到运动RAO，通过与试验值的比较（如图5），得出μ的选取规律。

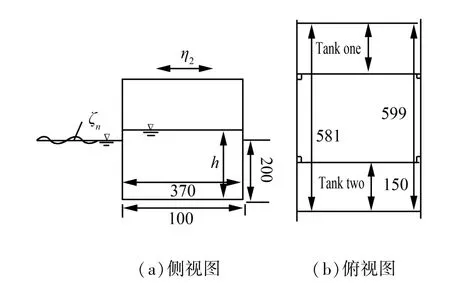
图3 带液舱驳船横荡运动模型Fig.3 Box-shaped hull section

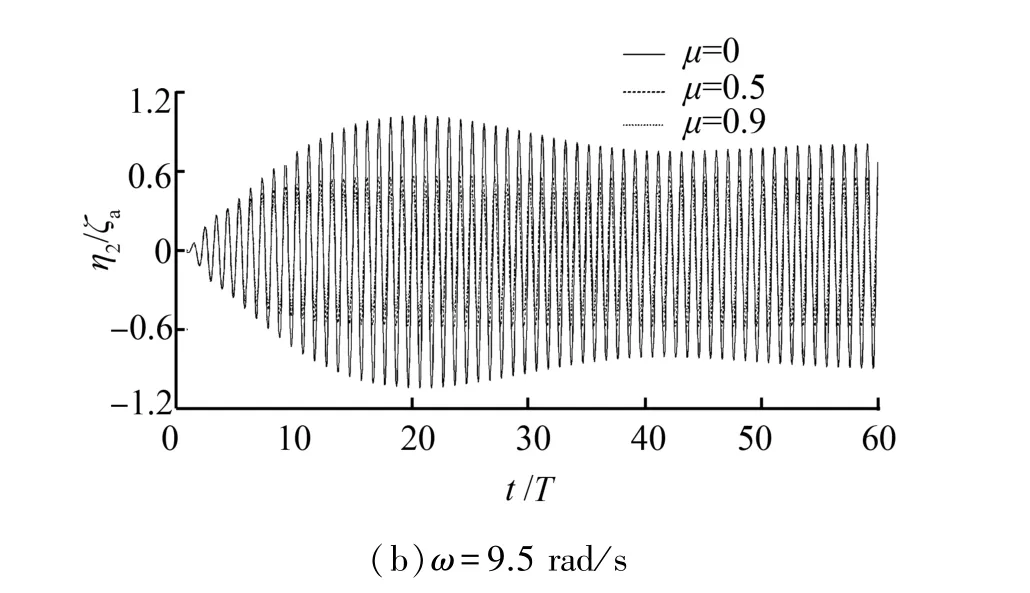
图4 液舱晃荡与驳船横荡耦合运动时历曲线Fig.4 Time history of sloshing and sway coupling motion

从图4中可看出，在不考虑液舱晃荡能量耗散时（μ＝0），即使在模拟60个周期后，时历曲线仍然难以达到稳态并且呈现明显的包络特性。一方面是由于液舱晃荡共振效应导致的。另一方面是由于数值计算中未考虑液舱晃荡能量耗散的影响［8］。实际上，在晃荡过程中由于流体粘性及波浪破碎等因素，能量耗散是伴随着整个流体晃荡过程的，在经历多个周期之后，液舱内部流体运动趋于稳态。增大μ的取值不但改变横荡运动幅值且可更快速的使多频非简谐时历曲线衰减成单频的稳态简谐曲线，这说明本文能量耗散条件的作用效率较高。

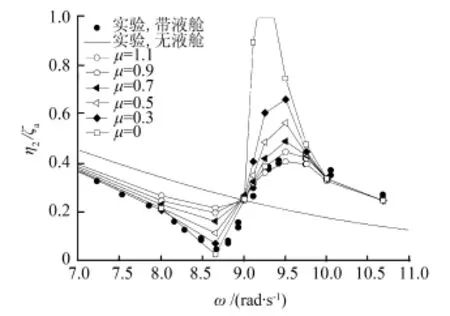
图5 μ对带有液舱的浮体横荡运动RAO的影响Fig.5 Sway coupling motion RAO with different μ

从图5中可看出，当入射波频率ω向晃荡一阶固有频率ω1＝8.65 rad／s靠近时，液舱晃荡减小了驳船的横荡运动。在大于ω1附近，液舱晃荡明显加剧了浮体的横荡运动，可以看出ω＝9.5 rad／s附近，带有液舱的浮体运动RAO出现峰值，增大μ可以减轻晃荡对船体横荡运动的影响。在不考虑液舱晃荡能量耗散影响时，数值结果与试验结果在峰值附近差异较大，前者要明显大于后者。因此能量耗散系数μ的选取对计算精度的影响很大。

带液舱船体横荡运动RAO与不带液舱船体横荡运动RAO曲线在两曲线交点处发生明显分歧（该工况时在ω＝9.0 rad／s处），该频率定义为交界频率ωd。当波频小于ωd时，液舱晃荡减弱了船体横荡运动；当波频大于ωd时，液舱晃荡反而加剧了船体横荡运动。交界频率 ωd处对应的横荡运动RAO幅值几乎不受能量耗散系数 μ的影响。当ω ＜ωd时，μ按晃荡固有频率处误差最小选取μ＝0.3与试验值吻合较好，当ω＞ωd时μ按RAO曲线峰值处误差最小选取μ＝0.9与试验值吻合较好。可发现，规则波中对液舱晃荡与船体耦合运动进行数值模拟时，μ的取值是有规律的，可能对于某些工况来说μ需进一步修正，但暂可认为该规律是最合适的。

3.2 LNG船的试验验证

为了验证上文所述规则波中能量耗散系数μ选取的规律，选取一个典型的具有试验数据的LNG运输船如表1，3种液舱装载工况（R0，R2，R3）进行研究如表2所示。由于只关注横浪规则波下LNG船的横荡及横摇运动，船艏及船尾形状对运动影响较小，因此可用二维数值模型进行计算。计算中LNG船按排水体积及形宽不变等效为吃水相同的驳船，液舱形状按实际LNG船液舱给定。

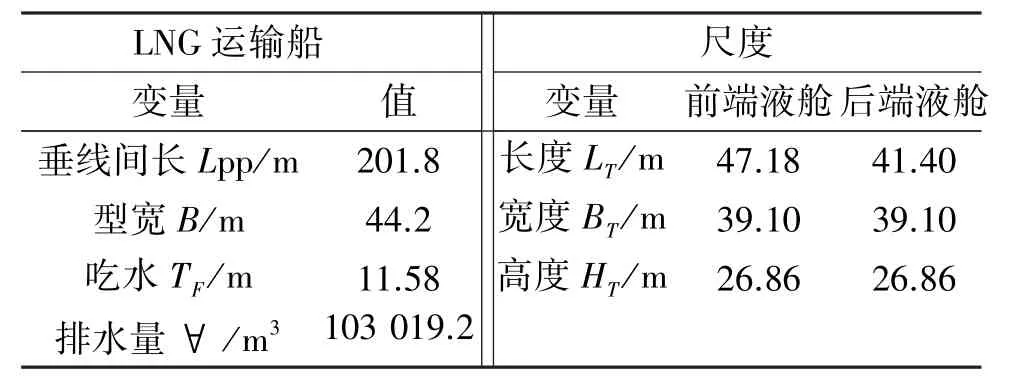
表1 LNG船和液舱的特征尺度Table 1 Main dimensions of LNG carrier and its tanks

表2 计算参数Table 2 Numerical parameters used in the computation

将数值结果与文献［20］试验结果进行对比（如图6）可看出，横摇运动RAO与试验值吻合较好，验证了能量耗散系数μ选取规律的适用性。虽然现有的模型不能对自由表面做精确的模拟（未考虑波浪破碎、砰击等作用），但并不影响对液舱晃荡与船体耦合运动的计算，而这才是主要目的。

图6 LNG船横摇运动RAO的比较Fig.6 Comparison of roll motion RAO of an LNG carrier

3.3 不规则波中带液舱船体的耦合运动分析

为考察实际海况中的液货船耦合运动效应是否显著，研究时域结果特性及能量耗散条件的作用效果。计算了文献［11-12］中带液舱驳船（如图7）在不规则波中的运动，并与试验及频域结果进行比较。选用第17界ITTC推荐的JONSWAP海浪谱，选取中等海情的短期海况，浪向为横浪，谱峰周期为1.6 s，有义波高为0.06 m。液舱装载工况如表3所示，μ分别取0.0、0.3、0.5。

图7 带液舱驳船试验模型Fig.7 Barge model in the basin

表3 计算工况（h为舱内部水深，L是液舱宽度）Table 3 Calculated condition（h is water depth and L is width of tank）

影响耦合运动的能量耗散主要有2个方面：一是晃荡中由于液体粘性及波浪破碎等引入的能量耗散，二是由驳船外流场波浪力引起的横摇粘性阻尼。因此横摇阻尼系数Cd可按无液舱的驳船进行选取，文献［11］中发现Cd＝0.2时较适合当前海况。由于驳船较宽，加载液舱后会明显影响驳船横摇运动，对横荡运动影响相对较小，因此重点研究该驳船的横摇运动。图8、9是对舱晃荡与驳船横摇耦合运动时历曲线做交叉谱分析后得到的运动RAO与试验及频域结果的比较。

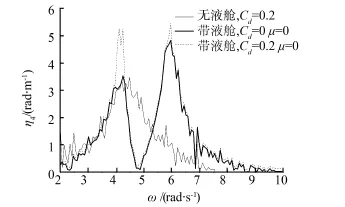
图8 Cd和μ对带液舱驳船横摇RAO的影响，h／L＝0.237 5Fig.8 Roll RAO of barge with tanks in different Cdand μ，h／L＝0.237 5

图9 μ对带液舱驳船横摇运动RAO的影响Fig.9 Roll RAO of barge with tanks in different μ

从图8中看出，不规则波中液舱晃荡在ω1附近的减摇效果明显，却在某些频率下加剧了驳船运动，这与规则波问题的分析一致。不考虑μ时，改变Cd对横摇运动RAO的第1个峰值影响较大，而对第2个峰值几乎没有影响。这是由于虽然在耦合运动中增加μ与Cd都可对横摇运动起到减摇的作用，但作用机理不同，产生的效果也不同。第1个峰值主要是驳船自身惯性引起，而第2个峰值是由液舱晃荡引起，Cd只能对前者产生作用。第2个峰值的能量耗散效应更为明显，因此在晃荡与船体耦合运动中仅仅通过加载横摇阻尼修正运动是不够的，晃荡能量耗散效应必须考虑。

从图9中可以看出，μ＝0.3，Cd＝0.2时较适合当前海况下驳船的横摇耦合运动，数值与试验结果吻合较好。μ的选择与充液比例无关，这在时域模拟中是十分方便及重要的。在不规则波中μ的取值是单一的，不需像在规则波中那样根据入射波波频与ω1的关系选取。频域结果与本文数值及文献［11-12］中的试验结果在第2个峰值处有较大差别。这种差别在2种充液状态下都有发生，其原因一是频域方法对横摇粘性和液舱晃荡粘性修正方法的局限性导致，二是舱内液体晃荡的多频振荡，使得在船体运动中叠加非单色入射波频的激励力成分，从而导致船体运动并非满足线性单频假设，因而对舱液流动采用线性频域理论处理会产生较大误差。

4 结论

本文基于时域势流理论，建立了一种新的计算液舱晃荡与船体非线性耦合运动的模型。新模型给出了一种改进的液舱壁面边界条件以近似晃荡能量耗散效应。通过与试验及频域结果的比较发现：

1）新模型成功地近似了液舱晃荡与船体耦合运动中液舱晃荡导致的能量耗散效应。只需经历短时间的数值模拟即可达到稳态。这种方法较之其他的基于粘性流体方程的模型效率更高。

2）分析了能量耗散系数μ修正耦合运动的作用及限晃效率，得到规则波及不规则波中较优化的能量耗散系数选取规律。其与液舱的湿表面形状及充液比例无关，且不受模型尺度的影响，这在时域数值模拟中是非常方便及高效的。

3）不规则波中非线性理论得到的带液舱船体横摇运动RAO由晃荡引起的第2个峰值要比线性频域理论计算的大，这与试验得到了一致的结果。因而对不规则波中舱液流动采用常规船体运动分析的线性频域理论处理会产生较大误差。

作为基础理论研究，本文模拟限于二维问题，由于耦合分析中晃荡总体载荷是关键因素，且船舶横摇受晃荡影响最显著，因此反应了最主要的影响因素，结论可指导进一步的三维分析。

［1］FALTINSEN O M，TIMOKHA A N.Adaptive multimodal approach to nonlinear sloshing in a rectangular tank［J］.Journal of Fluid Mechanics，2001，432：167-200.

［2］余建星，唐建飞，刘源，等.浮式液化天然气生产储卸装置重气泄漏扩散模拟分析［J］.天津大学学报，2013，46（5）：381-386.

YU Jianxing，TANG Jianfei，LIU Yuan，et al.Simulation and analysis of dispersion of heavy gas leakage from FLNG installation［J］.Journal of Tianjin University，2013，46（5）：381-386.

［3］洪亮，朱仁传，缪国平，等.波浪中船体与液舱晃荡耦合运动的时域数值计算［J］.哈尔滨工程大学学报，2012，33（5）：635-641.

HONG Liang，ZHU Renzhuan，MIAO Guoping，et al.Numerical calculation of ship motions coupled with tank sloshing in time domain based on potential flow theory［J］.Journal of Harbin Engineering University，2012，33（5）：635-641.

［4］李裕龙，朱仁传，缪国平，等.基于OpenFOAM的船舶与液舱流体晃荡在波浪中时域耦合运动的数值模拟［J］.船舶力学，2012，16（7）：750-758.

LI Yulong，ZHU Renchuan，MIAO Guoping，et al.Simulation of ship motions coupled with tank sloshing in time domain based on Open FOAM［J］.Journal of Ship Mechanics，2012，16（7）：750-758.

［5］FALTINSEN O M，TIMOKHA A N.A multimodal method for liquid sloshing in a two-dimensional circular tank［J］.Journal of Fluid Mechanics，2010，665：457-479.

［6］BOOKI K，YUNG S.Coupled seakeeping with liquid sloshing in ship tanks［C］／／Proceedings of the ASME 27th International Conference on Offshore Mechanics and Arctic Engineering.Estoril，Portugal，2008：15-20.

［7］MALENICA Š，ZALAR M，CHEN X B.Dynamic coupling of seakeeping and sloshing［C］／／Proceedings of the 13th International Offshore and Polar Engineering Conferece.Honolulu，Hawaii，USA，2003：486-492.

［8］HUANG S，DUAN W Y，MA Q W.An approximation to energy dissipation in time domain simulation of sloshing waves based on linear potential theory［J］.China Ocean Engineering，2011，25（2）：189-200.

［9］DATTA R，SEN D.The simulation of ship motions using a b-spline-based panel method in time domain［J］.Journal of Ship Research，2007，51（3）：267-284.

［10］YAN S，MA Q W.Numerical simulation of fully nonlinear interaction between steep waves and 2D floating bodies using the QALE-FEM method［J］.Journal of Computational Physics，2007，221：666-692.

［11］MOLIN B，REMY F，LEDOUX A，et al.Effect of roof impacts on coupling between wave response and sloshing in tanks of LNG-carriers［C］／／Proceedings of the 27th International Conference on Offshore Mechanics and Arctic Engineering.Estoril，Portugal，2008：15-24.

［12］MOLIN B，REMY F，RIGAUD S，et al.Ch.LNG-FPSO’s：frequency domain coupled analysis of support and liquid cargo motions［C］／／Proceedings of INAM Conference.Rethymnon，Greece，2002.

［13］WU G X，MA Q W，EATOCK T R.Numerical simulation of sloshing waves in a 3D tank based on a finite element method［J］.Applied Ocean Research，1998，20：337-355.［14］CHEN X B.Hydrodynamics in offshore and naval applications part 1［C］／／Proceedings of the 6th International Conference on Hydrodynamics，University of Western Australia.Perth，Australia，2004.

［15］MA Q W.Numerical simulation of nonlinear interaction between structures and steep waves［D］.London：City University，1998.

［16］段文洋.浮体大幅运动非线性水动力研究［D］.哈尔滨：哈尔滨工程大学，1995：67-68.

DUAN Wenyang.Nonlinear hydrodynamic forces acting on a ship undergoing large amplitude motions［D］.Harbin：Harbin Engineering University，1995：67-68.

［17］RANADEV D，DEBABRATA S.A B-spline based method for radiation and diffraction problem［J］.Ocean engineering，2006，33：2240-2259.

［18］MA Q W，YAN S.QALE-FEM for numerical modelling of non-linear interaction between 3D moored floating bodies and steep waves［J］.International Journal for Numerical Methods in Engineering，2009，78：713-756.

［19］GEAR W.Numerical initial value problems in ordinary differential equations［M］.Englewood Cliffs：Prentice-Hall，NJ，1971.

［20］MARIN.Seakeeping tests for the JIP SALT LNG carrier［R］.Report No.18127-1＆3-SMB，Jan.1st，2003.

Nonlinear time domain simulation of sloshing and coupled ship motion

HUANG Shuo1，2，3，DUAN Wenyang3，YOU Yage1，2，JIANG Jinhui4，WANG Wensheng1，2
（1.Key Laboratory of Renewable Energy，Chinese Academy of Sciences，Guangzhou 510000，China；2.Guangzhou institute of energy conversion，Chinese Academy of Sciences，Guangzhou 510000，China；3.College of Shipbuilding Engineering，Harbin Engineering University，Harbin 150001，China；4.Shanghai Shipping Scientific Research Institute，Shanghai 200135，China）

With the development of LNG carriers，this paper focuses on the study of the influencing characteristics of sloshing in the coupled nonlinear ship motions.The aim is to develop the time domain prediction techniques under both regular and irregular wave conditions.The energy dissipation was modeled by changing the boundary condition on tank solid boundaries.Under the linear free surface condition，to find out the potential，the fully nonlinear model was adopted for the inner tank flow and the boundary element model of Green function satisfying transient nonlinear body surface condition was used for external flow outside the tank.The boundary value problem was solved by the B-spline higher-order panel method.The ISITIMFB（iterative semi implicit time integration method for floating bodies）was applied to solve the body’s velocity and displacements.An extended principle to determine the dissipation coefficient μ is extracted and the effectiveness of this method was demonstrated from the comparison results of the experimental and numerical situation.

sloshing；energy dissipation；fully nonlinear model；time-domain coupled motion；LNG carrier；B-spline；ISITIMFB

10.3969／j.issn.1006-7043.201307076

O352；U661.1

A

1006-7043（2014）09-1045-08

http：／／www.cnki.net／kcms／doi／10.3969／j.issn.1006-7043.201307076.html

2013-07-31. 网络出版时间：2014-08-26.

国家自然科学基金资助项目（70271029，41106031）；国家973计划基金资助项目（2012CB723804）.

黄硕（1984-），女，助理研究员，博士；段文洋（1967-），男，长江学者，教授，博士生导师.

黄硕，E-mail：huangshuo＠ms.giec.ac.cn.