感应耦合电能传输系统输出功率调节方法

蔡 华 史黎明 李耀华

（1.中国科学院电工研究所电力电子与电气驱动重点实验室 北京 100190 2.中国科学院大学 北京 100049）

1 引言

感应耦合电能传输系统（Inductively Coupled Power Transfer,ICPT）基于电磁感应原理，可实现供电设备和用电设备之间在非物理接触情况下的电能传输，在易燃易爆、水下、自动化车间、电气交通等苛刻环境下具有显著优势，并获得了应用[1-4]。图1所示为感应耦合电能传输系统电路基本结构框图，交流电经整流得到直流电，经逆变和电容补偿后接入无接触变压器的一次侧，在无接触变压器二次侧感应出电压，经电容补偿和整流后得到直流电，供给负载。感应耦合电能传输系统中，根据负载需求调节输出功率是十分重要的内容之一。

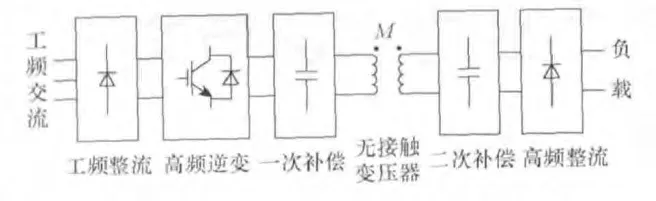
图1 ICPT典型结构Fig.1 Diagram of inductively coupled power transfer

图2所示为一种典型的电压型ICPT电路拓扑，在逆变器前加入一级 DC-DC电路，通过调节其输出电压或电流来调节系统输出功率。文献[5]提出一种电流型 ICPT拓扑和控制方法，通过升高或者降低输出电流来控制输出功率，该方法需要增加一级直流变换环节。文献[6]对既有的串串和串并两种电容补偿拓扑进行了分析，探讨了谐振频率下功率传输特性，没有深入研究如何高效调节输出功率。文献[7]描述了电流型无接触供电系统的一种移相控制策略，通过调整全桥逆变器桥臂直通时间控制传输功率。文献[8,9]描述了一种离散的能量注入控制的功率调节方法，逆变器处于软开关状态。文献[5,7]研究的均是电流型 ICPT系统，均需要很大的滤波电感。归纳常见的功率调节方法，主要有：调幅（Pulse Amplitude Modulation,PAM）[5]、调频（Pulse Frequency Modulation,PFM）[6]、移相调宽（Phase-Shifted Control,PSC）[7]，能量注入控制（Energy Injection Control,EIC）[8,9]。

图2 电压型串串补偿ICPT电路拓扑Fig.2 Circuit topology of ICPT with serial capacitor compensation on both sides

相比电流型ICPT系统，电压型ICPT系统无需笨重的滤波电感，且电压源更容易获得，因此本文以电压型电路拓扑 ICPT为研究对象，以串串电容补偿（SS）为例，结合实际系统参数，分析比较几种典型功率调节方法的特点，提出一种新型基于谐波的移相控制功率调节方法，利用谐波替代基波实现输出功率的调节。

2 电压型ICPT功率调节

为了实现感应电能传输的高功率因数和高功率密度，通常在无接触变压器的一次侧和二次侧均进行电容补偿，常用的补偿方式有并并补偿（PP）、并串补偿（PS）、串并补偿（SP）和串串补偿（SS）[10]。在这四种电容补偿方式中，只有采用串串补偿（SS），谐振电容的电容值才与负载以及无接触变压器一次侧和二次侧之间互感值无关，因此本文以串串补偿方式的电压型 ICPT进行分析，为了说明ICPT系统输出功率与其他变量的关系，在不考虑开关器件损耗的情况下，得基波等效电路如图3所示。

图3 串串电容补偿ICPT等效电路Fig.3 Equivalent circuit of ICPT with serial capacitor compensation on both sides

图3中，Lp、Ls、Rp、Rs分别为一次绕组和二次绕组自感以及相应电阻，M为一次和二次绕组之间的互感，Cp、Cs分别为一次和二次串联的补偿电容，Udc为直流电源电压，Up为逆变器输出电压基波成分有效值，ωs为供电角频率，fs为开关频率，fr为谐振频率，Re为等效负载电阻，URe为等效负载电压有效值。根据图中电路关系，可得系统输出基波功率Pout和传递效率η为

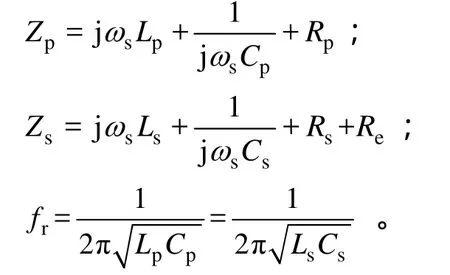
由式（1）和式（2）可知，输出功率Pout与供电电压Up的平方成正比，与开关频率fs成非线性关系。传递效率η和供电电压Up无关，与开关频率fs成非线性关系。根据表 1所示参数得无接触变压器的输出功率和传递效率与开关频率 fs的关系，如图4 所示。

表1 计算和实验参数Tab.1 Simulation and experiment parameters

图4 输出功率和传递效率与频率的关系Fig.4 Relationship of power and efficiency with frequency

由以上分析可知，在给定变压器和负载条件下要控制输出功率，可以调节逆变器的输出电压和开关频率。不同于基波频率仅为几十到几百赫兹的常规 PWM变流器，感应耦合电能传输系统基波频率一般为几十 kHz，采用的为谐振变流器，所以要采用方波调制[11]。要调节等效输出电压可以通过调节逆变器输出电压的幅值或者脉宽，前者可以在逆变器前加入一级 DC-DC电路，后者可用移相控制实现。调节输出频率可通过改变逆变器的开关频率实现。另外，还可以改变注入谐振电路的能量密度来实现离散的功率调节。

3 不同功率调节方法分析比较

3.1 调幅调功（PAM）

调节逆变器的输出电压幅值是最直接的功率调节方法，通常在逆变器前增加一级 DC-DC电路以控制逆变器输出电压幅值。逆变器输出方波电压，其占空比为50%。为了实现全功率范围的调节，常用Buck斩波降压电路，如图2所示。

Buck斩波电路中，电感Lb电流连续的情况下，逆变器输出基波有效值为

式中 D——Buck斩波器主开关S5的占空比。

输出基波功率

即只要调节Buck斩波器占空比D从0到1变化，就可以调节系统输出功率。

3.2 调频调功（PFM）

无需增加DC-DC环节，令式（4）中的D固定为 1，直接调节逆变器的开关频率 fs即可调节逆变器输出功率。输出基波功率可表达为开关频率的函数

即调节开关频率就可以调节系统输出功率。

3.3 移相调功（PSC）

移相调功方式中，各个开关管驱动脉冲占空比均为50%且频率不变，通过调节逆变器对管驱动脉冲的相位差来调节逆变器输出电压占空比，即令图2中S4和S2的驱动脉冲分别滞后S1和S3驱动脉冲一定相位角 α，实现输出基波电压的调节，其拓扑结构见图2中的逆变部分，各个开关管驱动脉冲及逆变器输出电压波形如图5所示。

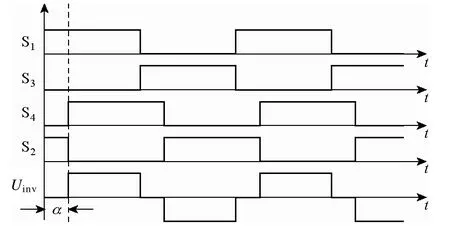
图5 移相控制示意图Fig.5 Diagram of phase-shifted control

对逆变器输出电压 Uinv进行快速傅里叶变换（Fast Fourier Transform,FFT）,得基波电压有效值为

输出基波功率为

即通过调节逆变器移相角α从0°～180°变化就可以调节输出功率。

3.4 能量注入控制调功（EIC）

以上三种方法可以连续调节输出功率，文献[8,9]提出了一种离散能量注入的功率调节方法，通过控制一次侧的能量注入来调节谐振电流的幅值，进而调节输出功率。该方法是一种闭环控制，通过输出电压反馈值和参考值的比较来选择是注入能量还是让谐振电流自由振荡耗散能量，根据谐振电流的正负决定需导通的开关对，从而实现软开关。

3.5 不同功率调节方法比较

PAM：输出功率由 DC-DC电路主开关器件占空比决定，增加了一级功率变换环节，增加了系统成本和复杂性，另外由于 Buck斩波器主开关器件工作在硬开关状态，增加了开关损耗。优点是逆变器无需参与功率调节，可以工作在软开关状态。

PFM：输出功率由逆变器开关频率决定，优点是比 PAM 少了一级功率变换环节，主要缺点是改变开关频率会影响无接触变压器的传递效率。随着开关频率逐渐偏离谐振频率，逆变器输出电压和电流相位差逐渐加大，功率因数降低，开关损耗和导通损耗均加大，传递效率降低。

PSC：输出功率由逆变器移相角决定，该方法中既没有PAM中额外的功率变换环节，也不受PFM中逆变器输出频率对变压器效率的影响，同时移相控制也较容易实现软开关[12]，具有电路简单，传递效率高的优点，可作为主要的功率调节方法。缺点是轻载时，软开关实现困难，开关损耗大。

EIC：输出功率由逆变器导通的密度决定，优点是功率调节过程中可以实现软开关，但是其功率调节是一种离散的控制方法，呈现有级调节的特征，最小控制周期是半个开关周期，输出电压的纹波相对较大。

表2总结对比了四种功率调节方法的优缺点。

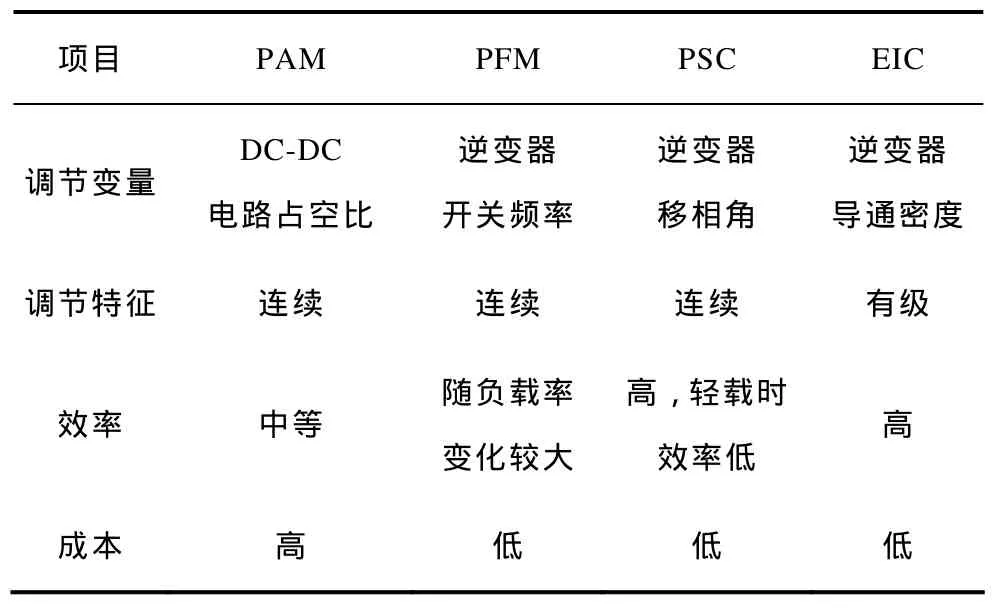
表2 不同功率调节方法比较Tab.2 Comparison of power adjustment method

4 基于谐波的移相控制方法

采用移相控制调功方法具有电路简单、开关频率固定、输出功率连续可调的优点。然而，在移相角较大时，软开关实现越来越困难，系统效率下降。

传统方法一般让开关频率等于或约等于谐振频率，采用逆变器输出电压的基波成分传递功率，而忽略了谐波的作用。基于移相控制的特点，考虑到方波输出电压中丰富的谐波含量，可利用谐波替代基波传递功率。通过降低开关频率，使k次谐波工作在谐振状态，采用移相实现功率调节，称为基于谐波的移相控制 （Harmonic based Phase-Shifted Control,HPSC）功率调节方法。此时，开关频率fs、所选择的谐波次数k与谐振频率fr的关系为

在不考虑逆变器死区影响的情况下，对不同移相角时逆变器输出电压波形进行FFT分解，得第k次谐波电压有效值Upk为

以零移相角下逆变器输出电压基波有效值为基准值，可得不同移相角下逆变器输出电压k次谐波电压（Upk）的标幺值

不同移相角下逆变器输出电压谐波含量分布如图6所示。

图6 不同移相角下逆变器输出电压谐波含量Fig.6 Harmonic content at different phase-shifted angle

当满足式（8）时，k次谐波下输出功率为

由式（10）和式（11）可得Pok的标幺值为

由式（12）知，理论上k次谐波所传递功率的最大值为额定功率的 1/k2，尽管如此，但是当输出功率较低时选用谐波传递功率，可显著降低开关频率，进而降低开关损耗，具有优越性。

由图6，当基波有效值Gu1低于k次谐波有效值Guk的最高值时，可控制开关频率降为谐振频率的1/k，使k次谐波处于谐振状态，用k次谐波替代基波传递功率，同时调节移相角在0~180°/k范围变化以调节输出功率。由于较大程度的降低了开关频率，因此开关损耗也降低。随着输出功率的减小，满足功率传递要求的谐波增多，可采用最高次谐波，进一步降低开关频率和开关损耗，因此需得到基波以及各次谐波合理的移相角范围。

定义基波切换角 α1k为从基波切换到 k次谐波时的移相角,令u11/G = k，得即在基波处于谐振状态下，其移相角大于α1k时，可切换为k次谐波传递功率。

定义k次谐波最大移相角为αk，在k次谐波处于谐振状态下，移相角大于αk时，可切换为k+2次谐波。令得

由图6，在180°移相角范围内各次谐波有效值按移相角度求余弦后的绝对值分布，谐波次数越高，达到同样幅值可选择的移相角越多。这里选择从0°到αk作为k次谐波谐振状态下移相角范围。各次谐波的基波切换角和移相角范围见表3。

表3 不同谐波的基波切换角及移相角范围Tab.3 Switching phase and phase-shifted range of different harmonic

由以上分析，基于谐波的移相控制有以下优点：

（1）开关频率显著降低，从而降低了开关损耗。

（2）具有更大的移相角范围，可获得更高的功率调节精度。如输出功率标幺值 Gpk在 1/52～1/32范围，即在三次谐波工作输出功率范围内时,由表3可知，采用基波传递功率时移相角范围为141°~156.9°，而采用三次谐波为 0~35.4°，在有限的数字控制器位数下，扩大了移相角范围，提高了控制精度。

（3）移相角度减小，更有利于逆变器工作在软开关状态，降低开关损耗。从表3可知，谐波次数越高，传递相同功率情况下，所需的移相角越小。

另外，实际逆变器中具有一定死区时间，降低了输出电压有效值，可将死区时间等效为移相角，从基波切换角和工作角范围中减去。

5 实验结果

实验中直流电源经三相不控整流桥得到，设定空载时直流母线电压 Udc为 300V，开关频率为14kHz（谐振频率的1/3），逆变器死区时间为2μs，其他实验参数同表 1。实验中以三次谐波为例，改变移相角调节输出功率，死区时间等效移相角为10.1°。实验结果见表 4，从表中可以看出，随着移相角度的增大，输出功率降低。图7所示为逆变器输出电压中三次谐波处于谐振状态下，移相角为1.9时，逆变器输出电压u和逆变器输出电流i波形,从图中可以看出电流频率为电压频率的3倍，即逆变器输出电压中的三次谐波处于谐振状态。

表4 三次谐波工作下移相角与输出功率Tab.4 Experiment with third harmonic HPSC

图7 三次谐波谐振下逆变器输出波形Fig.7 Inverter output waveforms when third harmonic component is at resonance

表4和图7表明，通过基于谐波的移相控制方法可以实现功率调节的目的。本文以串串补偿的感应耦合电能传输系统为对象进行了分析，但是由于基于谐波的移相控制本质是通过改变逆变器输出电压的有效值来调节输出功率，所以该方法容易扩展到其他补偿拓扑中去。

6 结论

本文提出了一种新型基于谐波的移相控制（HPSC）功率调节方法，通过降低开关频率，使所选择的谐波频率等于谐振频率，利用谐波替代基波传递功率，采用移相来调节输出功率。在此基础上，给出了各次谐波的切换移相角度以及各次谐波合理的移相范围。该方法降低了开关频率，可减少开关损耗，尤其解决了传统移相控制下轻载时效率低的问题。实验表明提出的方案可行，特别是供电系统在较轻负载下具有优越性。

[1] Kojiya T,Sato F,Matsuki H,et al.Automatic power supply system to underwater vehicles utilizing noncontacting technology[C].IEEE Techno-ocean,2004:2341-2345.

[2] Boeij J,Lomonova E,Duarte J,et al.Contactless power supply for moving sensors and actuators in high-precision mechatronic systems with long-stroke power transfer capability in x-y plane[J].Sensors and Actuators A: Physical,2008,148: 319-328.

[3] Meinss J,Bühler G,Czainski R,et al.Contactless inductive power supply[C].Magnetically Levitated Systems and Linear Drives,2006: 1-9.

[4] Covic G,Elliott G,Stielau O,et al.The design of a contactless energy transfer system for a people mover system[C].International Conference on Power System Technology,2000: 79-84.

[5] 孙跃,王智慧,苏玉刚,等.电流型 CPT系统传输功率调节方法[J].重庆大学学报,2009,32(12):1386-1391.Sun Yue,Wang Zhihui,Su Yugang,et al.Power transfer regulation mode for current fed CPT system[J].Journal of Chongqing University,2009,32(12): 1386-1391.

[6] 孙跃,夏晨阳,赵志斌,等.电压型 ICPT系统功率传输特性的分析与优化[J].电工电能新技术,2011,30(2): 9-12.Sun Yue,Xia Chenyang,Zhao Zhibin,et al.Analysis and optimization on power transmission characteristics for voltage-fed ICPT system[J].Advanced Technology of Electrical Engineering and Energy,2011,30(2): 9-12.

[7] 苏玉刚,王智慧,孙跃,等.非接触供电移相控制系统建模研究[J].电工技术学报,2008,23(7): 2-97.Su Yugang,Wang Zhihui,Sun Yue,et al.Modeling of contactless power transfer systems with a phaseshifted control method[J].Transactions of China Electrotechnical Society,2008,23(7): 92-97.

[8] Li H L,Hu A P,Covic G A.A power flow control method on primary side for a CPT system[C].International Power Electronics Conference(IPEC),2010: 1050-1055.

[9] Hao Leo,Li Aiguo,Hu Covic,et al.Development of a discrete energy injection inverter for contactless power transfer[C].Third IEEE Conference on Industrial Electronics and Applications,2008: 1757-1761.

[10] 周雯琪,马皓,何湘宁.感应耦合电能传输系统不同补偿拓扑的研究[J].电工技术学报,2009,24(1):133-139.Zhou Wenqi,Ma Hao,He Xiangning.Investigation on different compensation topologies in inductively coupled power transfer system[J].Transactions of China Electrotechnical Society,2009,24(1): 133-139.

[11] 张卫平.开关变换器建模与控制[M].北京: 中国电力出版社,2008.

[12] 初中原,沈锦飞,沈海明,等.基于 DSP的软开关移相控制100kHz逆变电源[J].电力电子技术,2008,142(1): 40-41.Chu Zhongyuan,Shen Jinfei,Shen Haiming,et al.Research on a 100kHz inverter power supply of soft-switching phase-shifted control based on DSP[J].Power Electronics,2008,142(1): 40-41.