油浸倒立式电流互感器主绝缘电场分析与优化设计

阎秀恪 孙 阳 于存湛谢德馨

（1．沈阳工业大学电气工程学院 沈阳 110870 2.特变电工沈阳变压器集团有限公司 沈阳 110144 3．辽宁省电力有限公司检修分公司 沈阳 110003）

1 引言

我国正在建设大容量、远距离、特高压的坚强国家电网，电压等级的提高，对电网中电气设备绝缘可靠性的要求也越来越高。电流互感器作为电网中的重要电气设备，一次侧与母线相连，一旦发生事故，后果非常严重[1,2]。目前电流互感器的发展趋势，倒立式电流互感器在国内外的应用越来越广泛。该类型产品区别于传统的正立式结构，将二次绕组与一次绕组集中置于整个产品的上部，避免了正立式结构主绝缘位于产品底部易受潮的环节，减少了主绝缘因受潮而被击穿的可能性，但同时也给产品的绝缘设计和工艺制造增添了一定的难度。倒立式电流互感器根据其绝缘介质的不同又可分为 SF6气体绝缘和油纸绝缘两种。近年来，针对 SF6电流互感器电场分析与绝缘优化设计的研究较多[3-5]，主要是通过在绝缘瓷套内加设屏蔽罩以及在法兰外加设屏蔽环来改善电场分布。油浸倒立式电流互感器的绝缘结构不同于 SF6电流互感器，通常采用电容型绝缘结构，即在绝缘油纸中通过增设电容屏来改善主绝缘内部的电场分布。关于油浸倒立式电流互感器电场分析与优化设计的研究较少，但实际产品运行事故却时有发生，且绝缘事故占有较大比例[6,7]。

油浸倒立式电流互感器增设电容屏的方法通常分为两种：一种是在二次侧下引线部位的绝缘油纸中增设端屏[8,9]，这样只是改善了下引线部分的电场分布，却忽略了二次侧绕组部位，而该处往往是导致事故发生的关键部位；另一种则是在整个主绝缘中增设主电容屏，并且在主屏端部加屏蔽环以避免尖端放电[10,11]。增设主屏虽然增加了主绝缘的包扎工艺，却能够改善主绝缘整体的电场分布。主屏式结构的油浸倒立式电流互感器结构模型较为特殊，不易达到较高的计算精度，关于其电场计算与绝缘设计的研究很少。

本文提出了一个有限元法与解析法相结合、分层分段计算电场的模型，利用 ANSYS软件计算一台220kV主屏式结构油浸倒立式电流互感器的电场分布，并以影响绝缘性能的主要变量——屏间绝缘厚度和屏间梯差作为优化变量，采用RBF神经网络动态响应模型结合遗传算法的智能优化算法对主屏式绝缘结构进行了优化设计。

2 物理模型

油浸倒立式电流互感器主绝缘结构如图1所示，整体成倒置的吊环状。主电容屏以串联形式嵌入主绝缘中，最外层屏接高电位，最内层屏接地。相邻两个电屏及其中间绝缘部分就构成一个电容器，这样就形成了一个由多个电容器串联的回路。

3 电场计算

本文考虑的是油浸倒立式电流互感器在工频耐压试验条件下的电场分布情况，而工频条件下的电场问题可近似为准静态场问题[12,13]，静电场对应的边值问题为

式中， V(I)为每层电屏的电位，由该层屏间电容C(I)串联分压求得

屏间电容C(I)可以由数值法和解析法求得。

图1 油浸倒立式电流互感器主绝缘结构示意图Fig.1 Main insulation of oil-immersed inverted current transformer

以本文计算的220kV油浸倒立式电流互感器为例，由于采用主屏式绝缘结构，主绝缘中设置多个电容屏，各屏间绝缘厚度大约在0～20mm之间，而主绝缘从上端环部到下端引线部，整体高度接近4m，尺寸相差很大，如果整体采用三维有限元计算，单元剖分无法达到较高的计算精度。因此本文将模型分层分段处理，将环部与下引线部分分开，又将环部的每一层分开，针对每层取四分之一建立三维模型，计算三维电场分布；对于下引线部分，基于其轴对称结构，进行二维电场有限元分析。

3.1 解析法求解电容

如图1所示，屏间电容 C(I)由环部电容 Ch(I)和引线电容Cy(I)并联组成式中，环部电容 Ch(I)又由内圆筒电容 Ca(I)、外圆筒电容Cb(I)和拐弯处电容Cw(I)并联组成。而环部和下引线之间过渡部分的电容不易确定，采取在外圆筒电容中减去与引线重叠部分的电容 Cs(I)的方法来等效，如图2所示。

图2 等效电容示意图Fig.2 Equivalent capacitance sketch

3.2 数值法求解电容

屏间电容也可以由有限元法计算得到，基于ANSYS软件将整个主绝缘按其屏间绝缘厚度分层建立模型，将各层绝缘的表面视为电容屏，单独计算各层屏间电容，选取相邻两个电容屏上的节点定义成组件，以内屏为地，利用CMATRIX宏命令求解。

3.3 实例分析

本文以一台 220kV油浸倒立式电流互感器为例，计算电场分布，其主要参数见表1。

表1 互感器主要参数Tab.1 Parameters of the current transformer

其中屏间绝缘厚度和屏间梯差等变量如图3所示。本文按照工程惯例，五个主屏间的绝缘厚度和梯差按均值情况计算，之后对其进行优化设计。分别采用解析法与数值法计算屏间电容，结果见表2。

图3 屏间绝缘厚度和屏间梯差示意图Fig.3 Sketch of thickness and gradient difference between two adjacent screens

表2 两种求解屏间电容方法的对比Tab.2 Comparison between two methods for capacitance calculation （单位: pF）

由表2可以看出，两种方法的计算结果基本一致，本文采用解析法对屏间电容的计算具有足够的精度和可行性。

由屏间电容串联分压得到各屏激励电位，利用ANSYS软件对环部各层和引线部分分别建模并进行有限元计算。图4为环部一层的三维网格剖分图，可以看出，网格细密而均匀，如果将电流互感器整体进行三维剖分，无法达到这样的精度。

图4 环部一层网格剖分图Fig.4 The 3D meshes of one layer of central loop

通过可视化处理，计算得到的环部各层绝缘的电场分布基本相同，整体趋势由内向外逐渐降低。图5为电场强度最大的第一层（最内层）绝缘环部的电场分布，其余四层类同，不再列出。

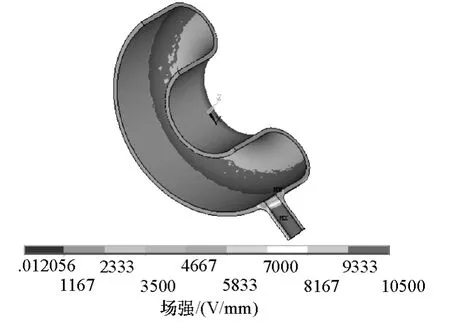
图5 环部第一层电场分布Fig.5 Electric field distribution of the first layer of central loop

可以看出，油浸倒立式电流互感器环部的电场较为集中在各层内圆筒与外圆筒交接的环型部位的内表面和下引线部分的内表面，其场强最大值位于下引线内表面，为10 500V/mm。

下引线部分电场分布的整体趋势与环部相同，电场较为集中在端环表面和各层电容屏表面，如图6所示，最大值为10 495V/mm。

图6 下引线及端环附近电场分布Fig.6 Electric field distribution of down-lead and shielding ring

电流互感器环部三维电场计算与下引线二维电场计算得到的场强最大值均位于下引线最内层屏表面的同一位置，图5和图6中最大场强的微小误差源于三维剖分与二维剖分的差异。

基于电流互感器环部与下引线的结构特征，其场强可视作呈径向分布，因此工程上通常关注其径向电场强度[8]，径向场强可由下式计算

式中 U——屏间电压；

Rp——计算位置的半径；

R1——内屏半径；

R2——外屏半径。

按上式计算下引线部分各屏表面的电场强度，得到各层最大场强。由有限元法计算得到各层绝缘最大电场强度的离散解，将计算结果进行比较见表3。两种方法的计算结果基本一致，验证了本文提出的分层分段计算的有限元模型的精度和可行性。

表3 均值情况下各层绝缘电场强度最大值Tab.3 Maximum electric intensity of each layer insulation（单位: V/mm）

4 主绝缘优化设计

4.1 影响绝缘性能的主要因素

由于采用电容型绝缘结构，电容屏的数量、长短、位置就成为绝缘设计的关键。工程上通常为了设计方便和制作工艺简单，电容屏设计采用等绝缘厚度、等梯差原则，但这并不意味着均值情况为最佳选择。屏间绝缘厚度影响绝缘效果，理想情况是屏间绝缘厚度尽可能的小[9]，但会导致主屏个数的增加，提高了生产成本和绝缘包扎的难度。而在屏数恒定的情况下调整屏间绝缘厚度和梯差可以改善电场分布，这就意味着在成本不变的情况下，提高了产品的绝缘可靠性。

4.2 优化模型与参数设计

因此，本文在主屏个数恒定，总绝缘厚度和总梯差一定的条件下，以各屏间绝缘厚度和屏间梯差为优化变量，以最大电场强度为目标函数对主绝缘结构进行优化设计。优化计算模型为

式中 n——电流互感器主屏个数；

R——总绝缘厚度；

D——总梯差；

ri——各层屏间绝缘厚度；

di——屏间梯差；

rmin,rmax——屏间绝缘厚度和的上、下限；

dmin,dmax——屏间梯差的上、下限。

多次的计算和分析表明，屏间绝缘厚度对屏间电压分布的不均匀度影响较大，同时端环表面的电场强度又和该端环处屏间电压密切相关，继而影响电场分布。另外考虑到制造工艺的限制，本文对所研究电流互感器的优化变量的变化范围设定如下：

4.3 优化过程

由于优化设计变量较多，电场分析计算量大，采用单一的随机类优化算法会消耗大量的系统资源和计算时间，因此本文采用基于径向基函数（RBF）神经网络动态响应模型[14-19]结合遗传算法的优化策略。即在满足约束条件的样本空间中，采用RBF神经网络建立响应模型，重构目标函数。在样本空间中采用遗传算法寻优，种群个体的目标函数值由重构目标函数计算得到。而样本空间和响应模型则跟随每次迭代的最优点的位置不断更新、细化，具体策略如下：

（1）以主绝缘中的最大电场强度为目标函数，采用本文提出的电场计算模型，由解析法计算屏间电容及各屏的激励电位，由有限元模型计算主绝缘电场分布，得到最大场强。

（2）确定满足优化变量约束条件的初始采样空间，离散采样空间，随机采样。

（3）将样本点（即主绝缘设计方案）载入步骤（1）中的电场计算模型，计算其目标函数值。

（4）将样本点及对应的目标函数值带入 RBF神经网络中，通过学习训练得出重构目标函数，确定响应模型。

（5）在采样空间中生成遗传算法的初始种群，通过进化寻优得到当前的最优点，寻优过程中个体的目标函数值由重构目标函数计算得到，无须进行有限元计算，大大减少了计算成本。

（6）将步骤（5）中由遗传算法得到的最优点载入步骤（1）中的电场计算模型，计算其目标函数值，并与上一次的最优点相比较，判断是否满足如下收敛条件

若满足，则 xk为最优解（即最优设计方案），迭代结束，输出最优方案，否则跳至下一步（其中ε1、ε2为设定的误差）。

（7）以当前最优点为中心将采样空间缩小0.618倍。

（8）提高精度离散采样空间，随机采样，返回步骤（4）。

4.4 优化结果

通过上述优化过程的迭代计算，最终得到最优方案见表4。

表4 优化结果Tab.4 Optimization results

由表4可以看出，最优方案的主绝缘最大电场强度降低了 10.1%。方案中屏间绝缘厚度由内向外逐渐增加，最内层屏间绝缘厚度相对较小，其它屏间绝缘厚度均匀递增。而屏间梯差由内向外呈现先增后减的趋势，这为油浸倒立式电流互感器的设计和制造提供了指导和参考。

图7和图8分别为优化后主绝缘环部第一层和引线部分的电场分布。

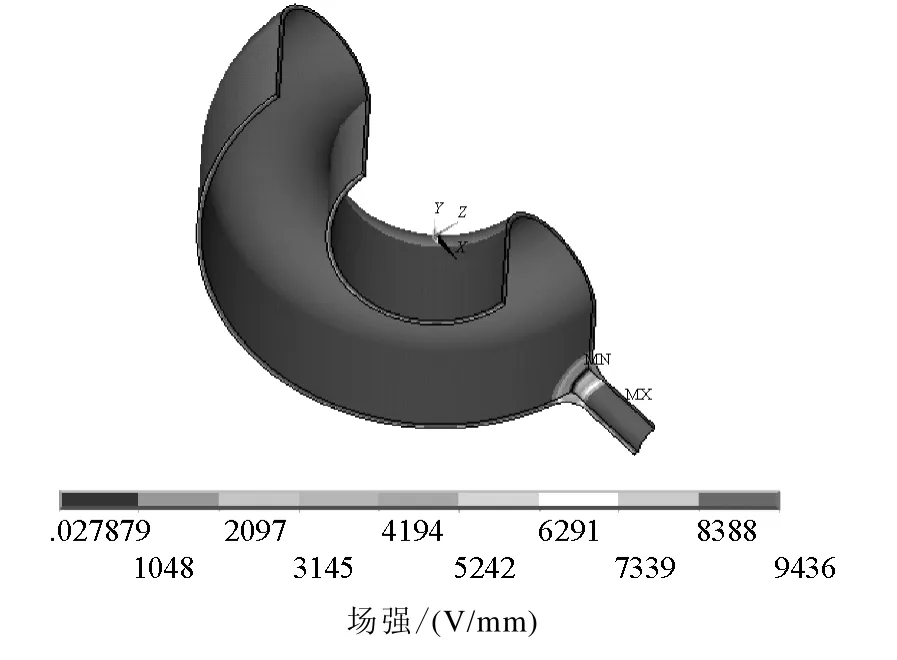
图7 环部第一层电场分布（优化后）Fig.7 The electric field distribution of the first layer of central loop(after optimization)

图8 引线部分电场分布（优化后）Fig.8 The electric field distribution of down-lead(after optimization)

由上面两图可以看出，优化后不仅电场强度降低了，主绝缘中的电场分布也更为均匀了。

5 结论

本文针对主屏式结构油浸倒立式电流互感器的结构特点，提出有限元法与解析法相结合的电场计算模型，分层分段计算了主绝缘中的电场分布。在电场分析的基础上，以各主屏屏间绝缘厚度和屏间梯差为优化变量，对主绝缘结构进行了优化设计。优化方案表明，屏间绝缘厚度由内至外逐渐增加、屏间梯差由内向外先增后减的设计，将使主绝缘内的电场强度降低，电场分布更加均匀，这为油浸倒立式电流互感器的设计和制造提供了理论指导和设计参考。

[1] 王世阁.倒置式电流互感器运行状况分析及提高安全运行性能的建议[J].变压器,2009,46(9): 64-68.Wang Shige.Operation analysis of inverted current transformer and suggestion to improve operational safety[J].Transformer,2009,46(9): 64-68.

[2] Satish M Mahajan,Diego M Robalino.Thermal modeling of an inverted-type oil-immersed current transformer [J].IEEE Transactions on Power Delivery,2010,25(4): 2511-2518.

[3] 王仲弈,马志瀛,顾沈卉,等.550kV SF6绝缘电流互感器的电场计算分析[J].华北电力大学学报,2005,23(sup): 71-74.Wang Zhongyi,Ma Zhiying,Gu Shenhui,et al.Electric field calculation and analysis of 550kV SF6current transformer[J].Journal of North China Electric Power University,2005,23(sup): 71-74.

[4] 王世山,李彦明,佟威,等.SF6电流互感器电场计算及其结构优化[J].电瓷避雷器,2003(4): 22-24.Wang Shishan,Li Yanming,Tong Wei,et al.Electric stress calculation and design optimization of SF6current transformer[J].Nsulators and Surge Arresters,2003(4): 22-24.

[5] 罗青林,刘玉凤,330kV SF6电流互感器电场计算及绝缘结构分析[J].变压器,2001,38(4): 16-19.Luo Qinglin,Liu Yufeng.Calculation of electric field in a 330kV SF6current transformer and its insulation structure analysis[J].Transformer,2001,38(4):16-19.

[6] 邹彬,郭森,袁聪波,等.一起 220kV 油浸倒立式电流互感器故障原因分析[J].变压器,2010,47(2):69-71.Zou Bin,Guo Sen,Yuan Congbo,et al.Fault analysis of 220kV oil-immersed inverter-type current transformer[J].Transformer,2010,47(2): 69-71.

[7] 陈瑞国,韩洪刚,孙艳鹤.220kV油浸倒立式电流互感器故障原因分析[J].变压器,2010,47(5): 68-71.Chen Ruiguo,Han Honggang,Sun Yanhe.Problem analysis of 220kV oil-immersed inverter-type current transformer[J].Transformer,2010,47(5): 68-71.

[8] 尚耀辉,赵建洲,刘亚亚,等.绝缘油纸电流互感器的绝缘设计[J].电力电容器与无功补偿,2009,30(3):25-27.Shang Yaohui,Zhao Jianzhou,Liu Yaya,et al.The insulation design of oil-paper insulation current transformer[J].Power Capacitor & Reactive Power Compensation,2009,30(3): 25-27.

[9] 魏朝晖.油浸倒立式电流互感器设计[J].变压器,2000,37(9): 6-9.Wei Zhaohui.Design of oil immersed inverted current transformer[J].Transformer,2000,37(9): 6-9.

[10] 互感器制造技术编审委员会.互感器制造技术[M].北京: 机械工业出版社,1998.

[11] 肖耀荣,高祖绵.互感器原理与设计基础[M].沈阳:辽宁科学技术出版社,2003.

[12] 杨茜,郭天兴,刘海,等.110kV电流互感器电场分析与绝缘结构改进[J].电力电容器与无功补偿,2010,31(1): 31-34.Yang Qian,Guo Tianxing,Liu Hai,et al.Electric field analysis and insulation structure improvement for 110kV current transformer[J].Power Capacitor &Reactive Power Compensation,2010,31(1): 31-34.

[13] 马爱清,郑勇,江秀臣,等.MPCG算法在GIS三相共罐式 SF6高压断路器电场计算中的应用[J].中国电机工程学报,2007,27(24): 5-10.Ma Aiqing,Zheng Yong,Jiang Xiuchen,et al.Application of MPCG aligorithm to three dimensional electric field calculation of SF6circuit breaker in three-phase-in-one-tank GIS[J].Proceedings of the CSEE,2007,27(24): 5-10.

[14] 曹云东,刘晓明,刘冬,等.动态神经网络法及在多变量电器优化设计中的研究[J].中国电机工程学报,2006,26(8): 112-116.Cao Yundong,Liu Xiaoming,Liu Dong,et al.Investigation of a dynamic nerual network approach and its application of multivariable optimization to electric apparatus[J].Proceedings of the CSEE,2006,26(8): 112-116.

[15] 李岩,王东风,焦嵩鸣,等.采用微分进化算法和径向基函数神经网络的热工过程模型辨识[J].中国电机工程学报,2010,30(8): 110-116.Li Yan,Wang Dongfeng,Jiao Songming,et al.Thermal process identification using differential evolution algorith and radial basis function neural network[J].Proceedings of the CSEE,2010,30(8):110-116.

[16] Chang G W,Chen Cheng I,Teng Yu Feng.Radialbasis-function-based neural network for harmonic detection[J].IEEE Transactions on Industrial Electronics,2010,57(6): 2171-2179.

[17] S Gholizadeh,E Salajegheh,P Torkzadeh.Structural optimization with frequency constraints by genetic algorithm using wavelet radial basis function neural network[J].Journal of Sound and Vibration,2008,312(1-2): 316-331.

[18] JBarry Gomm,Ding Li Yu.Selecting radial basis function network centers with recursive orthogonal least squares training[J].IEEE Transactions on Neural Networks,2000,11(2):306-314．

[19] 桂劲松,康海贵.结构可靠度分析的改进 BP神经网络响应面法[J].应用力学学报,2005,22(1):127-130.Gui Jinsong,Kang Haigui.Improved BP ANN response surface method for structural relibility analysis[J].Chinese Journal of Applied Mechanics,2005,22(1): 127-130.