强电流滑动电接触下最佳法向载荷

时 光 陈忠华 郭凤仪

（辽宁工程技术大学电气与控制工程学院 葫芦岛 125105）

1 引言

载流摩擦磨损是指处于电场中的摩擦副在电流通过条件下的摩擦磨损行为[1]，主要应用在大功率直流发电机、飞机执行器、风轮机和电力机车等高速受流领域[2-4]。电力机车的高速受流是指高速运行中受电弓滑板通过与接触网导线滑动接触获得电能并传递给电力机车的过程[5]。

低电流[6]、低载荷[7]与低滑动速度[8]的载流摩擦副研究装置，以及在此基础上得到的规律与特性，已不能满足高速机车的发展要求。受电弓滑板与接触网导线摩擦副的接触状态直接关系到机车的运行稳定性，同时摩擦副的摩擦磨损特性决定了机车连续运行的时间。

研究弓网系统的磨损特性、载流效率和载流稳定性具有重要意义。磨损特性决定了滑板与接触网导线的使用寿命，而载流效率与载流稳定性则是反映弓网系统受流质量的重要参数，良好的受流质量是机车高速平稳运行的前提[9-13]。

磨损特性不仅受速度、电流和法向载荷的影响，而且取决于摩擦副材料的相容性[14,15]。基于载流磨损机理[16,17]，很多学者研究了不同的载荷、电流和速度对摩擦副的影响。载流条件下的磨耗率主要有机械磨损和电磨损以及其交互作用共同决定，法向载荷过小时以电磨损为主，过大时以机械磨损为主，而在特定载流和速度条件下，法向载荷的大小决定了以哪种磨损方式为主，存在特定的法向载荷使得磨耗率最小[18,19]，亦能维持较高的载流稳定性[13]。如何减小磨耗率并同时保证受流质量是电力机车的高速受流过程需要解决的关键问题。

目前对磨损特性的研究多局限于定性分析各因素对磨耗的影响[1,19-21]，在受流质量研究方面的文献相对较少。文献[13]对铜基粉末冶金滑板的滑动电接触特性进行实验研究，通过引入电流相对稳定系数和载流效率值来评价受流质量，得到了载流效率随着大于70N法向载荷变化不是很明显，而电流的相对稳定系数更依赖于法向载荷的结论。

由于载流摩擦磨损的过程不易机理建模，本文采用支持向量机（SVM）对铜基粉末冶金滑板与铜锡接触导线载流对摩实验所得数据进行回归建模，采用DE-EDA算法寻找特定滑动速度和接触电流条件下的最佳法向载荷及其对应的Pareto最优解，使得滑板磨耗率与受流质量达到最优。

2 实验步骤

2.1 实验材料

导线材料采用铜锡合金导线，截面积为120 mm2，其性能参数见表1，滑板的化学成分和性能参数分别见表2和表3。

表1 铜锡导线材料性能参数Tab.1 Properties of Cu-Sn wire material

表2 滑板材料化学成分Tab.2 Chemical compositions of strip material(wt.%)

表3 滑板材料性能参数Tab.3 Properties of strip material

2.2 实验装置

自行研制的滑动电接触实验机如图1所示。利用该实验机进行接触导线和受电弓滑板的载流摩擦实验，在实验过程中可以实现对滑动速度、接触电压、实际接触电流、摩擦系数、温度和磨耗量等参量的实时在线测量和储存，以便于后期的数据处理。

图1 高性能滑动电接触试验机实物图Fig.1 High-performance sliding electrical contact testing apparatus

2.3 实验条件

所有的测试均是在实验室环境中进行的，摩擦副表面加入少量石墨作为润滑剂，法向压力载荷取值 30N、40N、50N、60N、70N、80N和 90N，通过改变砝码桶中的砝码来实现；电流取值 100A、150A、200A、250A和 300A；速度取值 40km/h、60km/h、80km/h和 100km/h。

2.4 参数定义

磨耗率定义为滑板相对于接触导线滑动 104km的质量损失，单位为g/(104km)。

接触电流的随机波动近似服从正态分布。为了衡量动态接触电流偏离静态给定电流的程度，引入了载流效率η，其计算公式为[13]

Is——静态给定电流值。

电流标准差SI，定义为

接触电流的载流稳定系数δ ，定义为

式（2）、式（3）中，δ 值越小说明接触电流的稳定性越高。

2.5 实验数据及分析

实验主要研究弓网模拟系统在各种工况下，磨耗率、载流效率和载流稳定性的变化关系。在法向载荷为60N时，磨耗率、载流效率和载流稳定性随电流和速度的变化关系，以及运行速度为100km/h，磨耗率、载流效率和载流稳定性随法向载荷和电流的变化关系如图2所示。图3是铜基粉末冶金滑板在固定法向载荷，不同接触电流和滑动速度条件下，磨损后的20 μm表面扫描电镜图片。

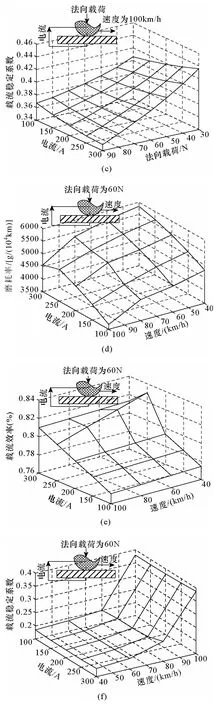
图2 不同条件下磨耗率、载流效率及稳定性变化特性曲线Fig.2 Curves of wear loss rate,current-carrying efficiency and stability

图3 磨耗表面扫描电镜图片Fig.3 SEM photographs of wear surface

分析图2中的变化趋势可知，法向载荷的大小直接影响磨损和载流性能。过小的法向载荷使得接触导线和滑板的离线机率较大，从而接触电流的稳定性变差，电弧侵蚀严重，滑板磨耗率也较高。法向载荷增大虽然可以降低滑板和导线之间的离线率[22,23]，从而减少了电弧和火花放电，使载流效率和载流稳定性得到提高，但是过高的法向载荷会破坏表面的润滑膜层，使得摩擦力变大，机械磨损加剧，适当的法向载荷可以使得磨耗率最小。

随着滑动速度的增加，图2中的磨耗率总体呈现变小的趋势，分析图13a、13b可知，在特定的法向载荷和电流作用下，速度较小时，图3a有明显的犁沟现象，此时以磨粒磨损为主要磨损方式；随着速度增加，表面温度升高，图13b形成了由石墨和氧化物构成的润滑膜层，能有效减小机械磨损；另一方面，速度的增加带来了接触导线与滑板离线率的增加，使得受流质量下降，但由于接触表面润滑膜层的隔离作用，对电弧和火花放电起到一定的抑制作用[24]，亦有效抑制了电磨损，此时以粘着磨损为主要磨损方式。

随着电流的增大，图2中载流效率及稳定性变化较小，但磨耗率明显增加。分析图3b、3c可知，强电流使得图3c中接触表面出现大的凹坑，电弧侵蚀严重，此时的滑板磨损主要为电弧侵蚀和粘着磨损。

3 支持向量机回归模型

SVM基于统计学习理论的VC维理论和结构风险最小化原则，其在小样本应用上更具有优势。本文采用的 SVM 的拓展机制，即支持向量回归（Support Vector Regression，SVR）的方法。用SVR建立回归预测模型，其基本思想是通过一个非线性映射φ，将回归样本数据映射到高维特征空间G中，并且在这个空间中进行线性回归。给定样本数据{xi,zi},i=1,…,l，其中 xi∈Rm，zi∈R，为期望值，l为样本总数。SVM采用下式来估计函数

式中，ω为G空间权矢量；b∈R为偏置。

对应优化目标为

式中，C为惩罚因子，实现在经验风险和置信风险的折中；iξ和*iξ为松弛因子；ε 为损失函数。

根据优化条件引入拉格朗日乘子α、α*，可以得到支持向量回归机的对偶问题

式中， Qij= K(xi,xj) = φ( xi)Tφ( xj)。

最终得到支持向量机的回归函数为

3.1 实验数据预处理

训练数据包括法向载荷、接触电流、滑动速度三个自变量和磨耗率、载流效率、载流稳定系数三个因变量。实际应用的弓网系统虽然是在高速、大电流的条件下，但运行速度和接触电流都在一定的范围内，为了加快收敛速度，故对SVR模型的训练数据采用归一化的预处理方式[25]。本文采用如下归一化映射

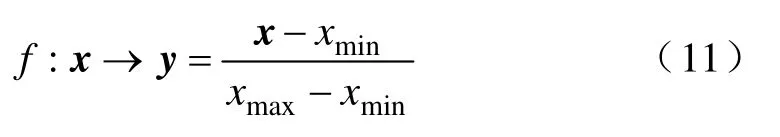
式中，x,y∈Rm；xmin=min(x)；xmax=max(x)；yi∈[0,1],i=1,…,l。

3.2 参数分析

在核函数的选择方面，有线性核函数、多项式核函数、径向基核函数和感知器核函数等，本文采用径向基核函数，即

另外，参数对回归的影响分析如下：

（1）惩罚参数 C使得模型复杂度和训练误差取一个折中，参数C过小，回归模型容易出现“欠学习”现象，而太大又会出现“过学习”，都将严重影响回归模型的泛化能力。

（2）损失参数ε控制着不敏感带的宽度，影响着支持向量的数目。ε值选得太小，回归估计精度高，但支持向量数增多，ε值选得太大，回归估计精度降低，支持向量数减少，支持向量机的稀疏性大。

（3）径向基参数γ决定了样本数据的分布或范围特性。

因此，参数C、ε和γ通过不同的方式控制着模型的复杂度和泛化能力，针对模型参数的选择已有多种方法，各有优缺点，本文采用遗传算法对其进行优化，其评价优劣的标准是在交叉验证[26]意义下的均方差（MSE）

3.3 参数优化

采用遗传算法分别对磨耗率、载流效率和载流稳定性三个 SVR回归模型的三个参数 C、ε和γ进行优化，遗传算法采用20位二进制编码，种群规模100，进化代数为100代，交叉概率0.7，变异概率0.05，5折交叉验证，最终得到的三个模型的训练参数见表4。

表4 参数值设置Tab.4 Parameters setting

4 基于DE-EDA的多目标优化

基于以上工作，得到了磨耗率、载流效率和载流稳定性的SVR回归模型。

4.1 目标函数

基于 SVR回归模型的最佳法向载荷优化问题可以描述为

式中，w为磨耗率；L为压力载荷；V为运行速度；I为电流；以上均为归一化后的数据。

在特定的滑动速度和接触电流情况下，即在点(Vi,Ij)，都对应一最优的接触载荷 lopt使得磨耗率最小、载流效率和载流稳定性最高。该问题可以描述为在点(Vi,Ij)上，寻找最佳法向载荷lopt对应的Pareto最优解问题。

4.2 DE-EDA算法

步骤1：种群初始化。(xj1,G,xj2,G,…,xjD,G)，j=1,…,NP。NP是决策变量的个数，D是决策变量的维数，G是进化代数；染色体采用实数编码的方法，每个染色体由xji=lowji+rand×(highji-lowji),rand为[0,1]内的随机数。

步骤2：适应度计算。非劣排序和适应度等级选择。

步骤3：对非劣解集进行统计学习，建立概率模型。

步骤4：设 0≤Pr≤1，当 rand＜Pr时，采用分布估计算法产生新样本，即对概率模型随机采样生成新个体；当 rand≥Pr时，按DE的变异、交叉生成新样本。使用模拟退火算法在线调整尺度因子：。其中，分别为设定尺度的上、下限，0≤β≤1为退火因子。

步骤5：当新生成的个体中有超越实际问题的取值范围的染色体或者基因位时，用下式修正

步骤6：将新种群和父代种群合并，组成 2NP的种群。

步骤7：非劣排序，产生子种群和非劣解集。

步骤8：满足终止条件，停止迭代；否则，转步骤3。

4.3 Pareto最优解与最佳法向载荷

图4 不同条件下Pareto解分布Fig.4 Pareto solutions under various conditions

5 结论

本文首先介绍自行研制的高性能滑动电接触磨耗实验机原理，进行了铜锡导线和铜基粉末冶金滑板的载流摩擦实验，获得了法向载荷、滑动速度和接触电流对滑板磨耗率、载流效率和载流稳定性的影响关系数据；然后应用支持向量机建立了以速度、载荷和电流作为自变量，磨耗率、载流效率和载流稳定性指标作为因变量的SVR回归模型，并通过差分进化-分布估计算法得到了在特定滑动速度和接触电流条件下，最佳法向载荷对应的滑板磨耗率最低、载流效率和稳定性最高的Pareto最优解，为具体工况下的法向载荷的设定提供参考。

[1] Tu C J,Chen Z H,Chen D,et al.Tribological behavior and wear mechanism of resin-matrix contact strip against copper with electrical current[J].Trans.Nonferrous Met.Soc.China,2008,18(5): 1157-1163.

[2] Takaoka M,Aso T,Sawa K.A commutation performance and wear of carbon-f i ber brush in gasoline[C].IEEE Holm Conference(47th),2001:44-49.

[3] Jensen M V R S.Long-term high resolution wear studies of high current density electrical brushes[C].IEEE Holm Conference(51st),2005: 304-311.

[4] Argibay N,Bares J A,Sawyer W G.Asymmetric wear behavior of self-mated copper fi ber brush and slip-ring sliding electrical contacts in a humid carbon dioxide environment[J].Wear,2010,268: 455-463.

[5] 于涤.高速接触网受流的理论分析[J].铁道学报,1998,20(5): 58-64.Yu Di.Analysis on catenary current-carrying theory of high-speed railway[J].J.Chin.Railway Soc.,1998,20(5): 58-64.

[6] Senouci A,Frene J,Zaidi H.Wear mechanism in graphite-copper electrical sliding contact[J].Wear,1999,225-229: 949-953.

[7] Kubo S,Kato K.Effect of arc discharge on the wear rate and wear mode transition of a copperimpregnated metallized carbon contact strip sliding against a copper disk[J].Tribology International,1999,32(7): 367-378.

[8] Bouchoucha A,Chekroud S,Paulmier D.Influence of the electrical sliding speed on friction and wear processes in an electrical contact copper-stainless steel[J].Applied Surface Science,2004,223:330-342.

[9] Ding T,Chen G X,Wang X,et al.Friction and wear behavior of pure carbon strip sliding against copper contact wire under AC passage at high speeds[J].Tribology International,2011,44: 437-444.

[10] Azevedo C R F,Sinatora A.Failure analysis of a railway copper contact strip[J].Engineering Failure Analysis,2004,11(6): 829-841.

[11] Jia S G,Liu P,Ren F Z,et al.Sliding wear behaviour of copper alloy contact wire against copper-based strip for high-speed electrified railways[J].Wear,2007,262: 772-777.

[12] Bucca G,Collina A.A procedure for the wear prediction of collector strip and contact wire in pantograph-catenary system[J].Wear,2009,266:46-59.

[13] 郭凤仪,姜国强,赵汝彬,等.基于相对稳定系数的滑动电接触特性[J].中国电机工程学报,2009,29(36): 113-119.Guo Fengyi,Jiang Guoqiang,Zhao Rubin,et al.Sliding electrical contact characteristics based on relative stability coefficients[J].Proceedings of the CSEE,2009,29(36): 113-119.

[14] Klapas D,Hackam R.Wear in a simulated power collection system for railways[J].Electric Contacts Colloquium Digest,1979,13: 81-83.

[15] Csapo E,Zaidi H,Paulmier D.Friction behaviour of a graphite-graphite dynamic electric contact in the presence of argon[J].Wear,1996,192: 151-156.

[16] Kubo S,Kato K.Effect of arc discharge on wear rate of Cu-impregnated carbon contact strip in unlubricated sliding against Cu trolley under electric current[J].Wear,1998,216: 172-178.

[17] Ding T,Chen G X,Zhu M H,et al.Influence of the spring stiffness on friction and wear behaviours of stainless steel/copper-impregnated metallized carbon couple with electrical current[J].Wear,2009,267:1080-1086.

[18] Zhao H,Barber G C,Liu J.Friction and wear in high speed sliding with and without electrical current[J].Wear,2001,249: 409-414.

[19] Wang Y A,Li J X,Yan Y,et al.Effect of electrical current on tribological behavior of copperimpregnated metallized carbon against a Cu-Cr-Zr alloy[J].Tribology International,2012,50: 26-34.

[20] Dinesh G,Jeffrey L.Behavior of Copper-Aluminum tribological pair under high current densities[J].IEEE Transactions on Magnetics,2009,45(1): 244-249.

[21] 郭凤仪,马同立,陈忠华,等.不同载流条件下滑动电接触特性[J].电工技术学报,2009,24(12):18-23.Guo Fengyi,Ma Tongli,Chen Zhonghua,et al.Characteristics of the sliding electric contact under different currents[J].Transactions of China Electrotechnical Society,2009,24(12): 18-23.

[22] 董霖,陈光雄,朱旻昊,等.地铁钢铝复合式第三轨/受电靴载流摩擦磨损特性研究[J].摩擦学学报,2007,27(3): 274-278.Dong Lin,Chen Guangxiong,Zhu Minhao,et al.Tribological characteristics between third rail and collector shoe under electric current[J].Tribology,2007,27(3): 274-278.

[23] 吴积钦,钱清泉.受电弓与接触网系统电接触特性[J].中国铁道科学,2008,29(3): 106-109.Wu Jinqin,Qian Qingquan.Characteristics of the electrical contact between pantograph and overhead contact line[J].China Railway Science,2008,29(3):106-109.

[24] Braunovic M,Konchits V,Myshkin N.Electrical contacts fundamentals,applications and technology[M].Boca Raton: CRC Press,2006.

[25] Ray S,Chowdhury S K R.Prediction of contact temperature rise between rough sliding bodies: an artificial neural network approach[J].Wear,2009,266: 1029-1038.

[26] Duan K,Keerthi S S,Poo A N.Evaluation of simple performance measures for tuning SVM hyperparameters[J].Neurocomputing,2003,51: 41-59.