基于fal函数的非线性PI控制器在DC-DC变换器中的应用
李 虹 尚佳宁 陈 姚 尚 倩 郝瑞祥
(1. 北京交通大学电气工程学院 北京 100044 2. 北京交通大学电子信息工程学院 北京 100044)
1 引言
在DC-DC变换器的控制策略中,PID控制以其简单有效,对模型误差具有鲁棒性以及易于操作的特点,得到了广泛的应用。
传统的PID控制器是利用实际值与设定值之间的误差,将控制误差(P)、误差积分(I)、误差微分(D)3个状态变量以线性组合方式构成控制量。但由于其在运行状态全局范围内,采用一种参数固定不变的线性控制方式,使得传统PID控制器常常引起系统快速性和超调量之间的矛盾[1-4]。而大量的分析研究表明,以某种非线性形式组合这3个状态变量,形成变增益PID控制将有助于提高控制效果[5]。
目前,国内外的一些专家学者已经对传统 PID控制进行了非线性的修正研究,这些方法大体可以分为两类[5]:第一类是模糊 PID类、神经网络 PID类[6,7],它是利用理论较为完善的模糊数学、神经网络对常规PID进行修正。这类方法的优点是非线性构造能力强,能够逼近任意的非线性函数,但这类方法的参数调试较为复杂,不利于工程应用;第二类是直接利用非线性函数进行修正[8-12],这类方法实现简便,但是非线性构造能力不如第一类方法。在PID控制中,最常用的是PI控制,本文从工程应用的简捷性要求出发,利用非线性fal函数,构造了非线性PI控制器。
本文第二节描述了非线性fal函数的特性,用仿真研究不同参数对非线性函数的影响,并且构建了非线性 PI控制器;第三节分别对基于非线性 PI控制器和传统PI控制的Boost变换器进行仿真并对比研究;第四节为实验验证;第五节为全文结论。
2 基于fal函数的非线性PI控制器
2.1 非线性fal函数[13]
fal函数是一种特殊的非线性结构,它是对“大误差,小增益;小误差,大增益”这一控制工程界经验的数学拟合[14]。fal函数具有快速收敛特性,因此成为常用的非线性反馈结构,文献[15,16]从非线性反馈效应的角度进一步阐述了这种结构。
fal函数表达式如下

式中,δ为线性段区间长度;a决定非线性函数fal的非线性度,是0~1之间的常数;ε为输入误差。
为直观描述fal函数的特性,利用Matlab/Simulink搭建fal函数模型。加入幅值为1,频率为 1rad/s的正弦信号作为输入,保持参数δ=0 .5不变,改变a,观测a变化对非线性fal函数的影响,输出如图1所示。
加入幅值为10,频率为1rad/s的正弦信号作为输入,保持参数 0.5a=不变,改变δ,观测δ变化对非线性fal函数的影响。输出波形如图2所示。
从图 1可知,曲线均在正弦函数幅值达到 0.5时产生转折,转折点之前为线性曲线,转折点之后曲线呈现出非线性特性。而a值越小,曲线的非线性程度就越大,0a=时,输出信号的非线性性质最明显,1a=时,输出和输入相同,表现为线性性质。由此可知,a的大小影响着fal函数的非线性程度。

图1 输出随a变化的曲线Fig.1 The output curve with the change ofa

图2 输出随δ变化的曲线Fig.2 The output curve with the change ofδ
图 2中,δ由 0.1变化至 7,可以看到在曲线分别在正弦函数幅值达到δ时出现转折,转折前呈现出线性特性,斜率为ε/δ1-a,转折后呈现非线性特性。由此可知,δ可以决定线性段区间的长度。
因此,当输入为误差信号时,可以通过调节fal函数的参数,使得反馈环节在误差较大时,产生较小的反馈增益,在误差较小时,产生较大的反馈增益,在保证系统的稳定性的同时,使系统快速的达到稳定。
2.2 非线性PI控制器
以fal函数作为非线性函数,非线性PI控制器的组合形式如下
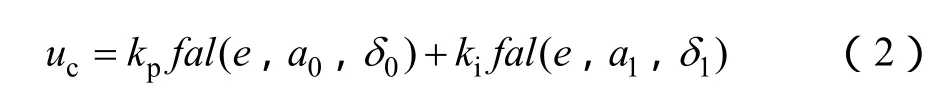
式中,e为误差信号,pk、ik分别为PI环节对应的系数。则非线性PI控制器构成如图3所示。
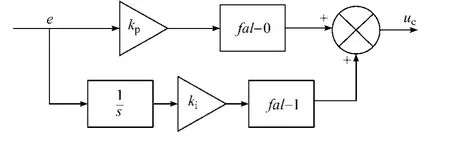
图3 非线性PI控制器结构Fig.3 The structure of the nonlinear PI controller
3 非线性PI控制器的应用仿真
本文以Boost变换器为研究对象,将非线性PI控制和传统PI控制分别应用于Boost变换器的反馈环节,对比两种控制在发生电压突变和负载突变情况下的动态调节过程非线性 PI控制的电路拓扑如图4所示。
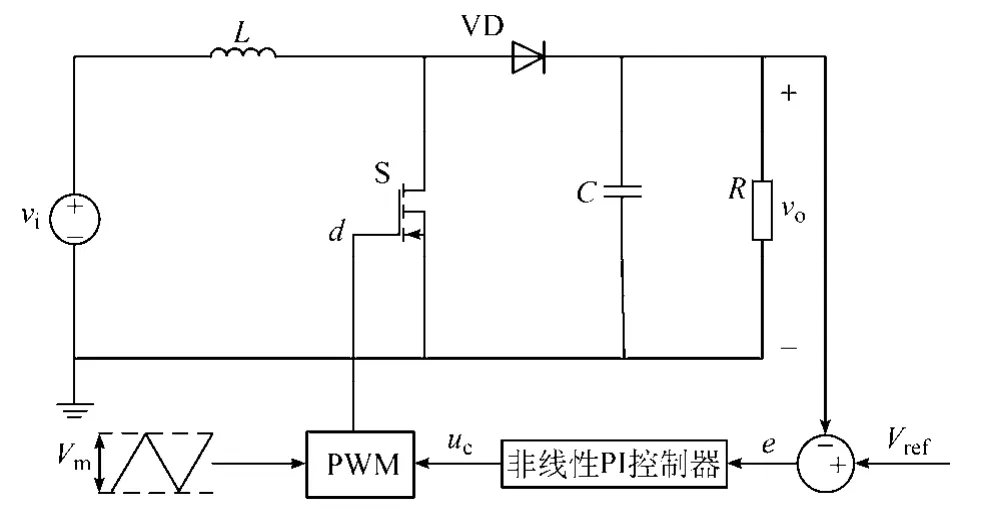
图4 非线性PI控制的Boost电路Fig.4 The Boost circuit with the nonlinear PI control
首先经过调试,将传统 PI控制参数kp、ki调至较好调制效果,此时kp=0 .006,ki=4 。然后将传统PI控制器替换为非线性PI控制器,在相同PI参数下,分别调节δ、a参数。调试参数如下:δ0=0 .01,a0=0 .6,δ1=0 .05,a1=0 .9。Boost主电路参数如表1所示。
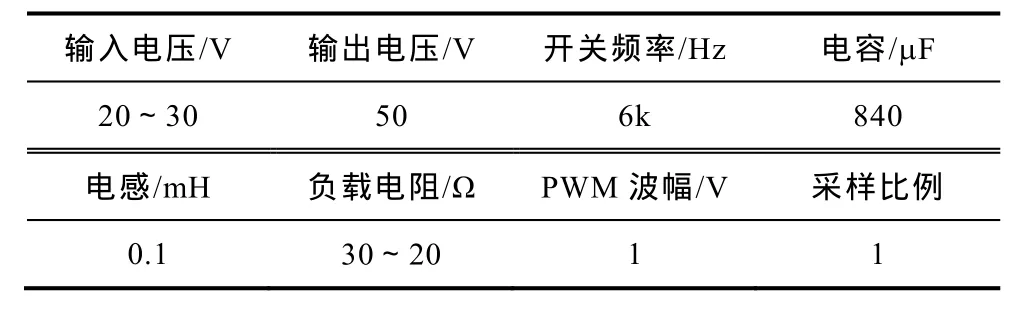
表1 仿真参数Tab.1 Simulation parameters
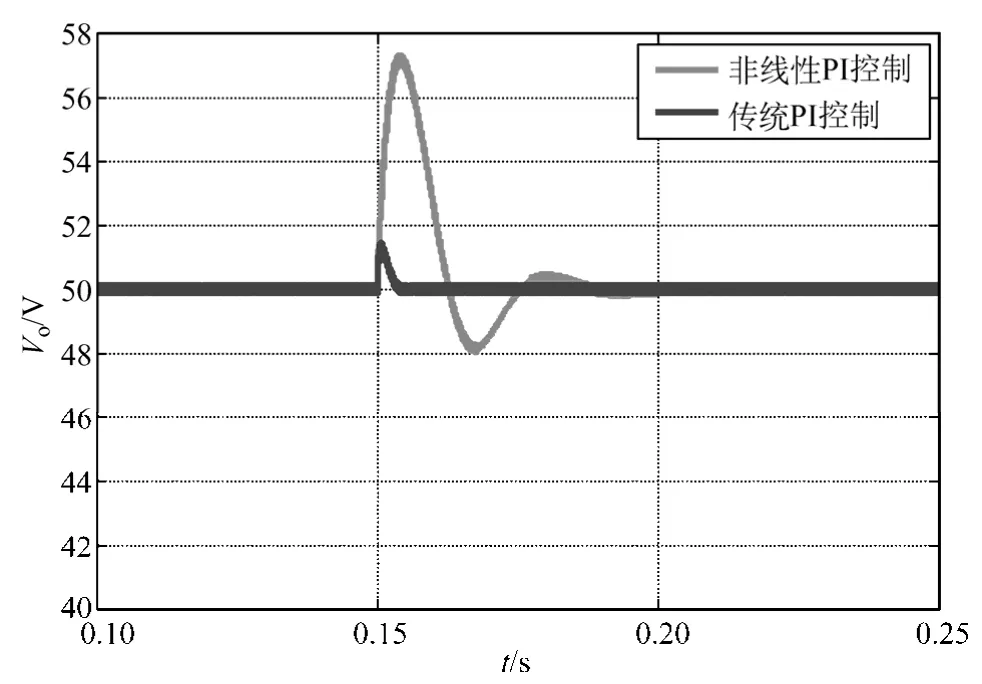
(a)输出电压波形

(b)比例环节的输出波形

(c)积分环节的输出波形

图5 电压突变波形Fig.5 The waveforms of the voltage jump
输入电压在0.15s时由20V突变至30V,传统PI控制和非线性PI控制输出电压波形如图5a所示,比例环节和积分环节波形如图5b、图5c所示。
在0.15s时负载电阻由30Ω突变至20Ω,PI控制和非线性PI控制输出电压波形如图6a所示,比例环节和积分环节波形如图6b、图6c所示。
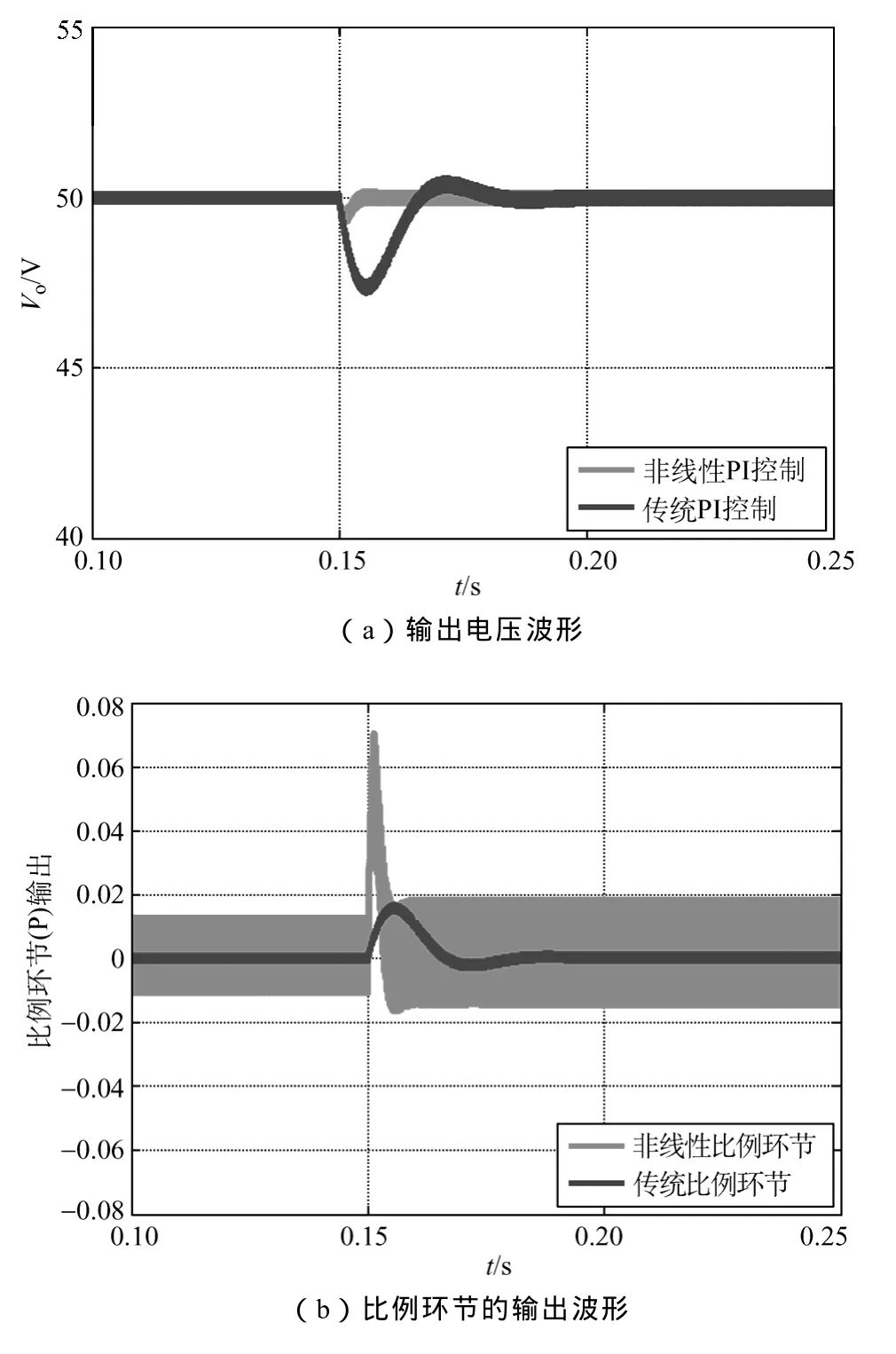

图6 负载电阻突变波形Fig.6 The waveforms of the load changing
综上仿真结果,对比结果如表2所示。
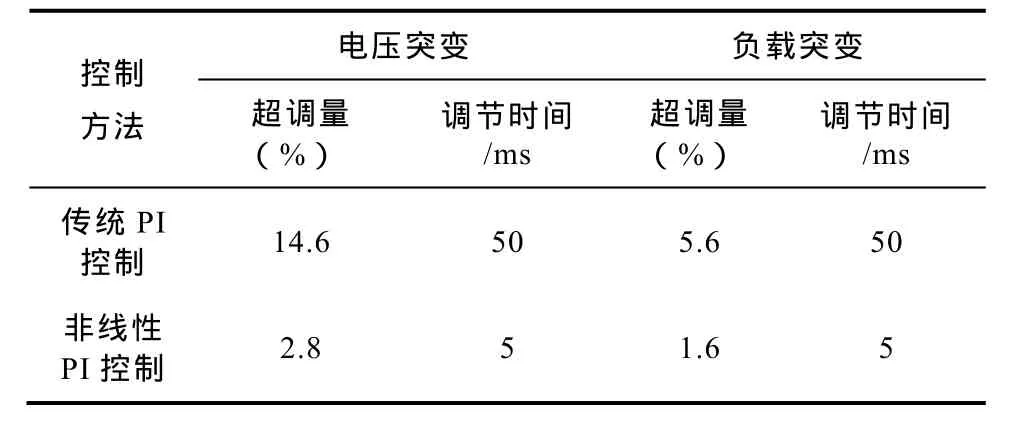
表2 动态响应仿真对比结果Tab.2 The simulation comparisons of dynamic response
输入电压由20V突变至30V情况下,Boost变换器用非线性 PI控制器产生 1.4V的超调,经过0.005s恢复至参考电压50V;传统PI控制产生7.3V的超调,经过 0.05s恢复至参考电压 50V。非线性PI控制相比PI控制超调量和调节时间更小。
在负载由30Ω突变至20Ω情况下,Boost变换器用非线性PI控制器产生0.8V的超调,经过0.005s恢复至参考电压50V,传统PI控制产生2.8V的超调,经过0.05s恢复至参考电压50V。非线性PI控制相比PI控制超调量和调节时间更小。
从两种扰动的比例环节和积分环节的输出波形来看,非线性fal函数的加入使得比例环节的输出在误差较小时的反馈增益变大,使得控制力度得以增强,超调不会太大;之后迅速恢复稳态,使得扰动的调节时间得以缩短。
4 实验验证
本文对非线性PI控制器进行了理论分析,以及在加入扰动情况下进行了传统 PI控制和非线性 PI控制电路的仿真对比。本文搭建Boost实验电路进行实验,对理论分析和仿真的正确性加以验证。

图7 实验平台Fig.7 The experimental platform
实验平台如图7所示。实验参数和仿真电路参数相同,同样进行了输入电压突变和负载突变两组实验。
输入电压由20V突变至30V时,传统PI调节和非线性 PI调节的波形如图 8所示;负载电阻由30Ω突变至20Ω时,传统PI调节和非线性PI调节的波形如图9所示。
从以下实验波形可以看到,非线性PI调节下的输出电压波形调节过程要优于传统 PI调节下的调节过程,与仿真结果相符合。


图8 输入电压突变的输出电压波形Fig.8 The output voltage waveform of the input voltage jump

图9 负载突变的输出电压波形Fig.9 The output voltage waveform of the load changing
5 结论
本文针对传统PI控制器的缺点,设计了基于fal函数的非线性PI控制器,并将非线性控制器应用于DC-DC变换器中。通过仿真和实验对比传统控制和非线性控制在电压和负载突变下的调制过程,结果表明非线性PID控制相对于传统PID控制对于外界扰动有更好的调制效果,具有较好的适用性和控制性能,为功率变换器的控制提供了一种新的选择。
[1] 任永平,李圣怡. 一种非线性 PID控制器及其参数分析[J]. 信息与控制,2005,34(4): 486-489.
Ren Yongping,Li Shengyi. Nonlinear PID controller and its parameter analysis[J]. Information and Control,2005,34(4): 486-489.
[2] 王伟,张晶涛,柴天佑. PID参数先进整定方法综述[J]. 自动化学报,2000,26(3): 341-355.
Wang Wei,Zhang Jingtao,Chai Tianyou. A survey of advanced PID parameter tuningmethods[J]. Acta Aut Omat Ica Sinica,2000,26(3): 341-355.
[3] 韩京清. 非线性 PID 控制器[J]. 自动化学报,1994(4): 487-490.
Han Jingqing. Nonlinear PID controller[J]. Acta Automatica Sinica,1994(4): 487-490.
[4] 王大彧,郭宏,刘治,等. 直驱阀用音圈电机的模糊非线性PID控制[J]. 电工技术学报,2011.
Wang Dayu,Guo Hong,Liu Zhi,et al. A fuzzy nonlinear PID control of voice coil motor used in direct drive valve[J]. Transactions of China Electrotechnical Society,2011.
[5] 尚宏,陈志敏,任永平. 一种新型非线性 PID 控制器及其参数设计[J]. 控制理论与应用,2009,26(4):439-442.
Shang Hong,Chen Zhimin,Ren Yongping. Parameter selection for a new class of nonlinear PID controller[J]. Control Theory & Applications,2009,26(4): 439-442.
[6] Ying H. Sufficient conditions on general fuzzy systems as function approximators[J]. Automatica,1994,30(3): 521-525.
[7] 孙增圻. 智能控制理论与技术[M]. 北京: 清华大学出版社,1997.
[8] 韩京清. 自抗扰控制技术[J]. 前沿科学,2007,1(1):24-31.
Han Jingqing. Auto disturbances rejection control technique[J]. Frontier Science,2007,1(1): 24-31.
[9] Margaliot M,Langholz G. Hyperbolic optimal control and fuzzy control[J]. IEEE Transactions on Systems,Man,and Cybernetics,Part A: Systems and Humans,1999,29(1): 1-10.
[10] Brian A,Bruce A W. Nonlinear PID control with partial state knowledge: damping without derivatives[J]. The International Journal of Robotics Research,2000,19(8): 715-731.
[11] 牛刚,冀捐灶,郭庆,等. 基于 DSC和数字预测非线性 PID控制的 DC/DC变换器[J]. 电气应用,2008(17).
Niu Gang,Ji Juanzao,Guo Qing,et al. DSC and Digital forcast Nonlinear PID control based on DC/DC convertor[J]. Electrotechnical Application,2008(17).
[12] 姜向龙,赵 金,万淑芸. 基于双曲正切函数的非线性 PI控制器及其在感应电动机矢量控制中的应用[J]. 电工技术学报,2004,19(6): 85-89.
Jiang Xianglong,Zhao Jin,Wan Shuyun. A nonlinear PI speed controller based on hyperbolic function and its application in the vector control of an induction motor[J]. Transactions of China Electrotechnical Society,2004,19(6): 85-89.
[13] 王宇航,姚郁,马克茂. Fal函数滤波器的分析及应用[J]. 电机与控制学报,2010,14(11): 88-91.
Wang Yuhang,Yao Yu,Ma Kemao. Analysis and application of Fal function filter[J]. Electric Machines and Control,2010,14(11): 88-91.
[14] 黄一,张文革. 自抗扰控制器的发展[J]. 控制理论与应用,2002,19(4): 485-492.
Huang Yi,Zhang Wenge. Development of active disturbance rejection controller[J]. Control Theory and Applications,2002,19(4): 485-492.
[15] Han J Q. Nonlinear design methods for control systems[C]. The Proceedings of the 14th IFAC World Congress. Beijing,1999: 521-526.
[16] Gao Zhiqiang,Huang Yi,Han Jingqing. An alternative paradigm for control system design[C].Proceedings of IEEE Conference on Control and Decision,Orlando,2001: 4578-4585.

