机器人避障的最优设计路径

汪慧玲

(咸宁职业技术学院，湖北 咸宁 437100)

引 言

随着科技的发展，机器人时代到来了。机器人的工作效率的提高与机器人行走时如何避开障碍物，选择最短路径紧密相关。给出如下场景：除了障碍物以外指定一点为机器人要到达的目标点，其中障碍物与目标点的距离至少超过L个单位。同时机器人的行走路径由圆弧和直线段组成，其中机器人转弯时走的是圆弧，因为不能走折线转弯，所以转弯时由直线和与其相切的一段圆弧构成，也可以由多个相切的圆弧相连接组成，但每个圆弧的半径最小为l个单位。机器人在行走时，与障碍物之间的距离至少为l个单位，否则发生碰撞，一旦发生碰撞，机器人就不能完成正常行走。针对这个具体问题，笔者进行了一些探讨。

一、机器人转弯时，沿最小半径的圆的切线走才为最短路径

1.猜想：如图1

图1

用MATLAB数学软件拟合得到图形2

图2

2.机器人避障问题实例分析1：O→A的最短路径求解

如图3(简化图形)，以P(80,210)的圆心，l=10个单位为半径做圆，点P是正方形的左上顶点，A(300，300).做圆P的切线OE与圆P相交于点E(x1,y1)，做圆P的切线AF与圆P相交于点F(x2,y2)。

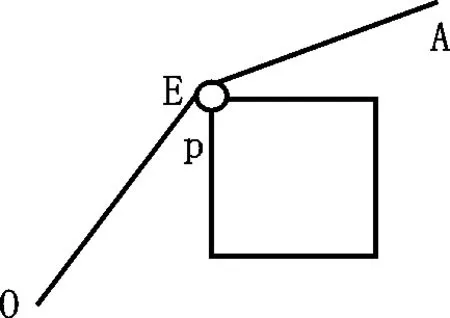
图3

利用简单的几何知识可列出以下等式：

通过MATLAB求解得出

解得直线AF的解析式为y=0.36x+191.76

起点坐标终点坐标路径长度线段一(0,0)(70.51,213.14)224.50弧长一(70.51,213.14)(76.61,219.41)9.05线段二(76.61,219.41)(300,300)237.49

所以总的路径长为224.50+9.05+237.49=471.04。则编号为6的三角形的右下顶点到线段AF的最短距离为22.06可以通过，EF的弧长为9.05，线段OE的长为224.50，线段AF的长为237.49。则点O运动到点A的路径长为471.04。

二、机器人从一点出发经过某一点到达另外一点的最短路径

1.机器人由A点出发经过M点后再到B点，因为机器人不可以走折线，经过M点时候,使M点位于半径为 的动圆的圆周上变动，如图4

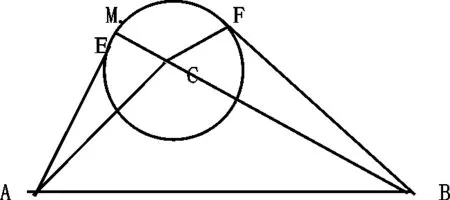
图4

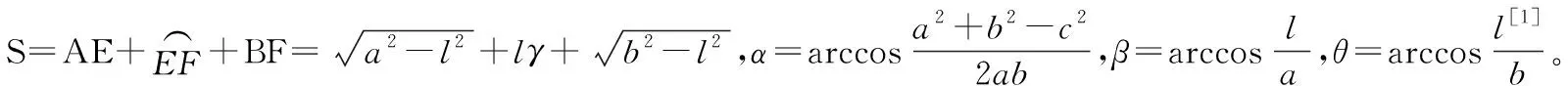
通过建立一个非线性规划模型，可以求出变动圆的圆心c(xc,yc)为：

2.机器人避障问题实例分析2：求O→A→B→C→O的最短路径的求解，

根据以上对从一点出发经过某一点到达另外一点的最短路径的求证，可以作出机器人行走的路径方式，每个经过的中间点都位于以10个单位为半径的圆周上。

类似实例一的计算方法，结合以上非线性规划模型，可以得到每一段直线和相应的圆弧的长度，从而得到机器人行走的最短路径。详细数据列举如下

起点坐标终点坐标路线长度直线一(0,0)(69.96,207.73)224.5圆弧一(69.96,207.73)(69.91,211.87)9.54直线二(69.91,211.87)(76.07,219.75)236.36圆弧二(76.07,219.75)(300.07,300.07)14.34

总的路径长为2828.18，因此O→A→B→C→O的最短路径长为2715.12.

三、结论

本文主要是在直线与圆相切而衔接的结构中，通过MATLAB数学软件作图证明得出机器人转弯时，沿最小半径的圆的切线走才为最短路径。利用解析几何的知识求出各个切点的坐标，结合两点之间的距离公式以及弧长公式分别算出线段和圆弧的长度，从而求得机器人避开障碍物由起点行走到另外一点的最短路径。针对机器人由起点行走经过途中若干个指定点最后到达终点的情况，在动圆半径不变的情况下，为了求的最短路径，建立了非线性规划数学模型求解。都通过MATLAB数学软件计算，给计算带来了快速便捷。试想将机器人在平面场景中行走的问题拓展到空间区域中。

参考文献：

[1]王新成.机器人避障路径的规划模型[J].温州职业技术学院学报,2014,(01):14～15.

[1]姜启源，谢金星，叶俊.数学模型9M].北京：高等教育出版社，2003.

[1]梁弘，翟步祥.高等数学基础[M].北京：北京交通大学出版社，2006.

[1]王沫然.MATLAB与科学计算[M].北京：电子工业出版社，2003.