一类分数次微分方程边值问题的解
代雨杭,胡平平,苏新卫
(中国矿业大学 理学院数学系,北京 100083)
1 引 言
本文研究下面问题
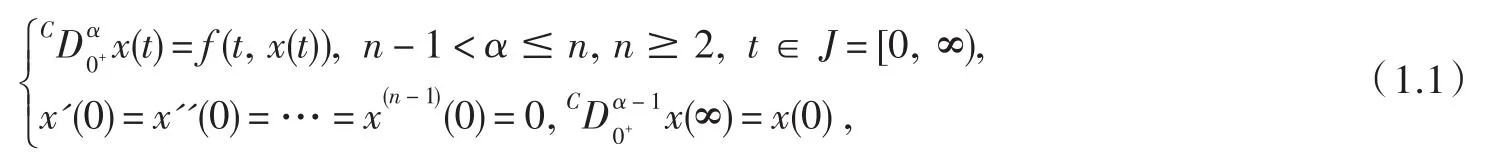
近几十年来,分数次微积分算子及分数次微积分方程因其在众多领域的应用而倍受关注,发展十分迅速[1-3].国内外许多学者致力于研究分数次微分方程的边值问题. 在文献[4]中,作者研究了无穷区间上分数次微分方程的边值问题,应用Schauder不动点定理及对角线化方法,证明了其有界解的存在性.无穷区间上分数次微分方程边值问题无界解的研究可参见文献[5-6].本文在合适的Banach空间中讨论问题(1.1)的解并允许解是无界的,基于Caputo导数更广泛的应用,不同于文献[5-6],问题(1.1)中的导数是Caputo导数且阶数是任意的.
2 有关引理
关于函数x(t)的 δ >0阶Riemann-Liouville分数次积分和Caputo分数次导数的定义可参见文献[1].
引理2.1[1]分数次微积分算子有如下性质,其中a>0是任意常数.
(1)对 f∈ L1(0, a), γ>δ>0,有和
(2)对 α > 0, β > 0, f(t)∈ L1(0, a)有
引理2.2[1]当且仅当f(t)=b+bt+bt2+…+btn-1,其中b∈R是常数,n是大于或等于δ012n-1i的最小整数.
由引理2.2可得
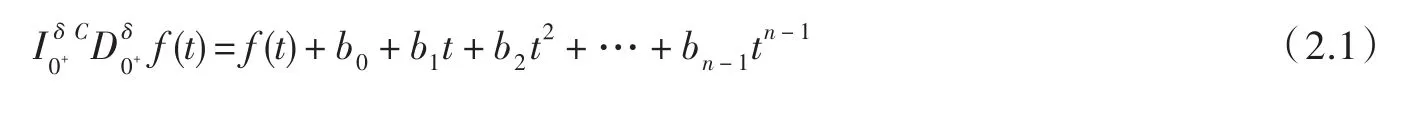
3 解的存在性
用C(J, R)表示定义在J上的连续函数空间. 定义空间
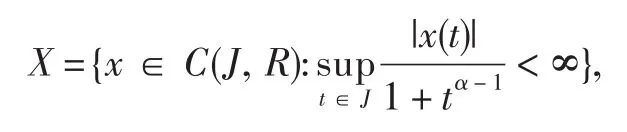
为证明本文的主要结果,我们需要下面的引理.
引理3.1[6]假设Y⊆X是有界集,若满足以下条件,则Y是相对紧集.
(2)任给 ε >0,存在 T =T(ε)>0,使对任意 t1, t2≥T 及 x (t)∈Y ,有
下面给出本文的主要结果.
定理3.1 设 有Lebesgue可积函数 a (t), b(t)∈L1(J, R+)满足 |f(t,x)|≤a(t)|x|+b(t),而且,2M∫0∞(1+tα-1)a(t) dt<1, ∫0∞b(t) dt<∞,则问题(1.1)至少存在一个解.
证 明首先注意到
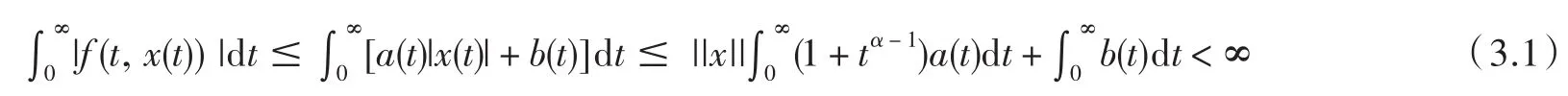
由引理2.1,引理2.2及(2.1)式易知(1.1)等价于下面的积分方程.
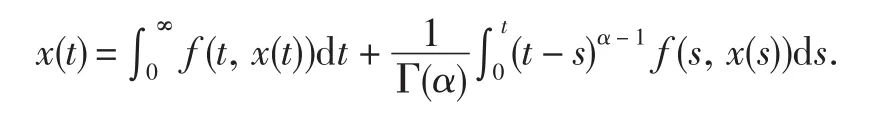
定义算子T如下:
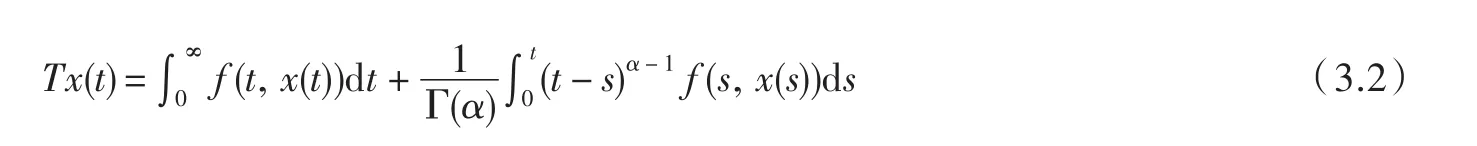
则算子T的不动点即是(1.1)的解.下面验证T满足Schauder不动点定理的条件.
首先,T:U→U.事实上,对 x(t)∈U,由条件及(3.1)(3.2)可知
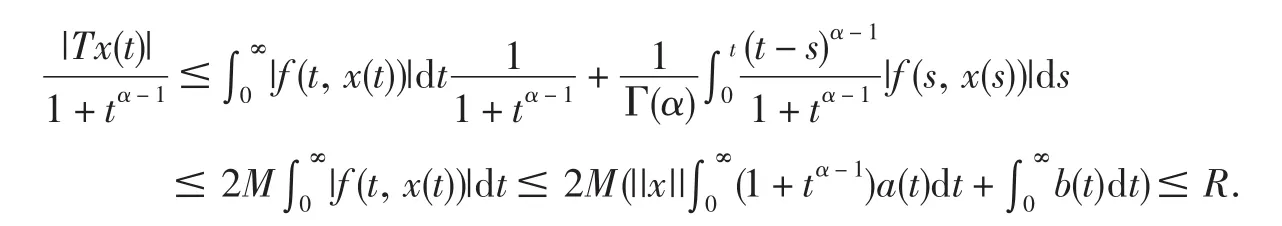
所以T:U→U.

T是连续的算子.事实上,对任意的x, y∈U有由Lebesgue控制收敛定理可得T是连续算子.
下面证明对Y⊆X是有界集,则TY是相对紧集,即证TY满足引理3.1.
首先设 I⊂J是紧区间,t1, t2∈I, t1 另一方面,由可积函数的绝对连续性得:任意ε>0,存在L>0,使得 同时,存在T1>0,使得t1, t2≥T1时有 又存在T2>L>0,使得t1, t2≥T2, s∈[0, L]时有 令 T>max{T1, T2},则当t1, t2≥ T 时,由(3.3)(3.4)(3.5)可得 所以易知引理3.1的(2)满足. 由上述证明可知,T满足Schauder不动点定理的条件,所以T在X中有不动点,即(1.1)存在解. [1]Kilbas A A,Srivastava H M,Trujillo J J.Theory and Applications of Fractional Differential Equations[M].Amsterdam:Elsevier B V,2006. [2]Podlubny I.Fractional Differential Equations,Mathematics in Science and Engineering(vol 198)[M].New York/London:Academic Press,1999. [3]Samko S G,Kilbas A A,Marichev O I.Fractional Integrals and Derivatives:Theory and Applications[M].Yverdon:Gordon and Breach,1993. [4]Arara A,Benchohra M,Hamidi N,et al.Fractional order differential equations on an unbounded domain[J].Nonlinear Anal,2010,72:580-586. [5]Zhao X K,Ge W G.Unbounded solutions for a fractional boundary value problem on the infinite interval[J].Acta Appl Math,2010,109:495-505. [6]Su X W,Zhang S Q.Unbounded solutions to a boundary value problem of fractional order on the half-line[J].Comput Math Appl,2011,61:1079-1087.





