基于COMSOL Multiphysics求解KdV方程

糜凯华

（昆明理工大学 电力工程学院，云南 昆明 650500）

很多物理现象都可以抽象成数学模型，建立起相应的偏微分方程即数学物理方程.然后对这些偏微分方程组求解得到真实世界的描述.Korteweg-deVires方程式由Korteweg和Vires于1895年对水波建模得到的，方程不考虑消耗并且波是永远运动的.孤立波是一种传播过程中形状、幅度和速度都保持不变的脉冲行波.它有内似粒子的性质，也叫孤立子.从物理学的观点看，孤立波是物质非线性效应的一种特殊产物，而从数学上看，它是某些非线性偏微分方程的一类稳定的、能量有限的非弥散解.孤立波在相互碰撞后，仍能保持各自的形状和速度不变.不仅在浅水波中有孤立波现象，在光纤通信、金属相变和神经传播等许多领域都有孤立波现象，即某种现象或信息以几乎恒定的脉冲形态传播.由于其具有这种特殊的性质，所以在等离子物理学、高能电磁学、流体力学和非线性光学等领域中得到广泛应用.由于非线性科研的发展，求解非线性方程的方法层出不穷，如：有限元法[1]、影射法[2]、非线性变换法[3]、同伦分析法[4]、双Jacobi椭圆函数展开法[5]、齐次平衡法[6]、试探函数法[7].而COMSOL Multiphysics的优点是求解偏微分方程或方程组，本文利用基于有限单元法的COMSOL Multiphysics有限元软件对KdV方程进行数值求解.

1 KdV方程及仿真模型的建立

1.1 KdV方程的建立

本文研究的KdV方程由Korteweg和他的学生deVires于1895年对水波建模得到.KdV方程经过变换可得到各种不同的形式.为了方便，本文取KdV方程表达式为

此KdV方程是一个典型的一维三阶偏微分方程.假设该孤立波在Ω=[ ]-8,+8的范围内周期性变化，其表达式为

初始条件的表达式为

以上三式即构成一个初边值问题.式（1）的解析解为

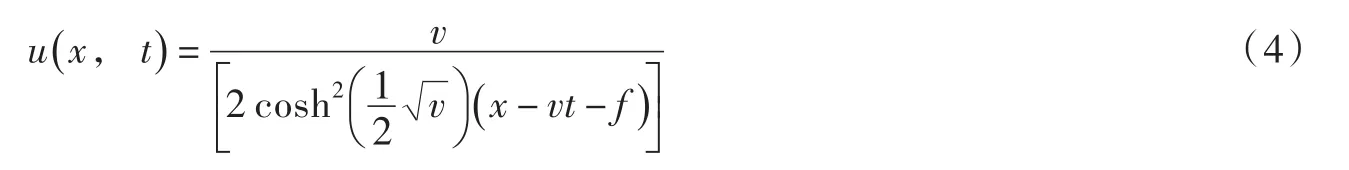
将初始条件式（3）与式（4）比较，可知两式并不一致.因此，就会在初始时刻产生两个迭加在一起的不同振幅和速度的孤立波.

1.2 仿真模型的建立

根据上述所建立的KdV方程，采用基于有限单元法的COMSOL Multiphysics软件建立有限元模型，其控制方程（也即物理场）选择Δu数学模块中Δu偏微分方程接口.因通常情况下，常见的有限元软件只能计算二阶偏微分方程或偏微分方程组，在COMSOL Multiphysics中，常规的应用也是二阶方程表述的模式.所以如何求解高阶偏微分方程是一个很棘手的问题.值得注意的是COMSOL Multiphysics软件具有强耦合[8]的计算功能，可以为高阶偏微分方程提供一种合理的求解方法.

对于我们所研究的三阶KdV方程，可以向方程中引入一些中间变量，通过变量代换的方式进行降阶，从一个三阶方程降阶得到一组存在耦合关系的二阶偏微分方程组，减少三阶偏微分方程求解的难度.为此，在选择控制方程时需要输入因变量个数为2，分别定义为u1和u2，并令中间变量u2=uxx，然后将u改为u1，即将所建立的KdV方程修改为一个偏微分方程组相应的初始条件也变为如下方程组

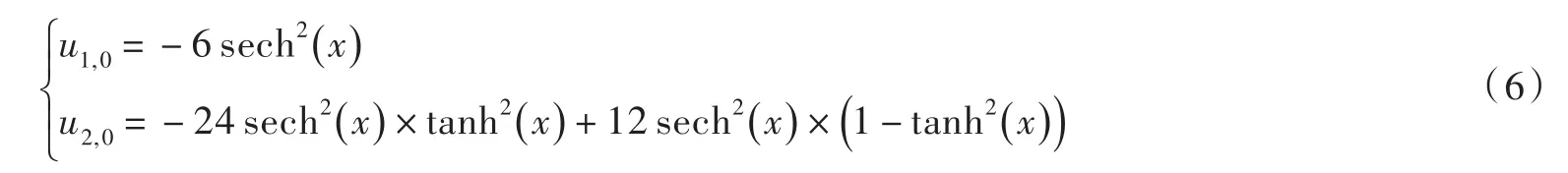
周期性边界条件变为如下表达式为

1.3 几何模型和有限元模型

所研究的问题属于一维情况，故在COM⁃SOL Multiphysics中建立的几何模型即是KdV方程中求解域Ω=[ ]-8,+8表示的一条线段.为了降低计算机的计算成本，加快模型的求解速度，同时也保证有一定的精度，划分求解域的最大单元尺寸为0.1，单元的划分总数为160个单元，其几何模型和有限元网格如图1和图2所示.

图1 KdV方程的几何模型

图2 KdV方程的有限元模型

1.4 初始条件和边界条件的设定

在COMSOL Multiphysics中直接将KdV方程的初始值式（6）输入初始值对话框.而周期性边界条件则需要选择几何模型中线段的两个端点，该条件保证两端边界解的连续性.所设置的初始值和周期性边界条件对应于上述推导得到的新的KdV偏微分方程组和定解条件，分别如式（5）、式（6）和式（7）所示.其控制方程描述如下：

2 数值结果与分析

通过上述所建立的有限元模型，在设定瞬态求解器的求解时间范围为0～2 s，时间间隔为0.025 s的条件下进行全局计算.通过求解，得到指定时间段内的波形分布，如图 3所示，分别表示第 0.0 s、0.3 s、0.7 s、1.1 s和1.2 s时的波形.为了更全面地了解碰撞过程，将所有时刻的波形分布用三维图的形式表示，如图4所示.

此外，为了更为清晰地分析数值模拟得出的孤立波传播特性是否与行波解所表达的物理意义相符.本文另取孤立波的形式为

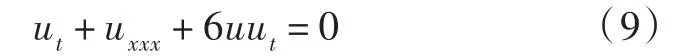
周期性边界条件与式（2）一样.式（9）的孤波解为

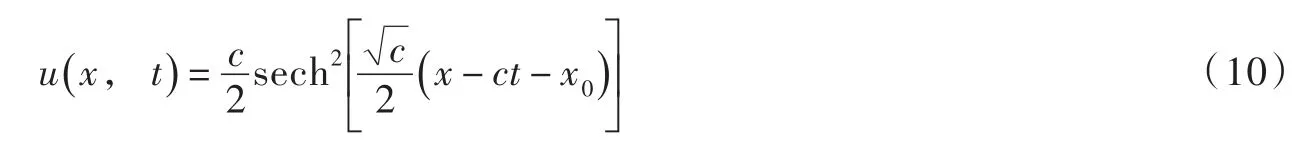
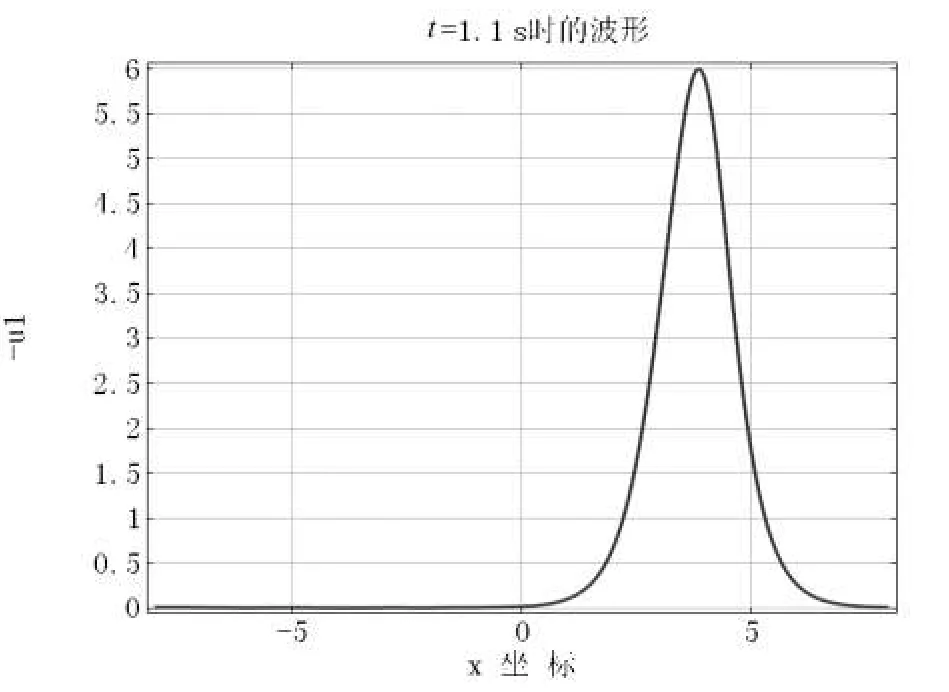
图3 孤立波在时间t=0 s、0.3 s、0.7 s、1.1 s、1.2 s的分布

式中c和x0是由初始条件决定的常数，x0为孤波的初始位置，为传播速度.

从图3可以清晰地看出：两个不同速度和振幅的孤子相互碰撞，相互穿过，相互之间没有影响.而且该孤立波不会发生消散.孤立波向右传播过程中，大波追赶小波，从而引起碰撞.

从图4可以看出：孤立子在一定的空间内会发生碰撞和重现，两个迭加在一起的孤立波以不同的速度传播，速度快的波穿越速度慢的波.

从图5和图6的比较中可发现，图5中孤立波的传播速度小于图6，即c越大，移动速度越快，波高越大，但宽度越窄.显然这和行波解表达的物理意义是相符的，即波高为c 2，波宽反比于.由此不难发现本文对KdV方程的数值模拟方法是正确的.

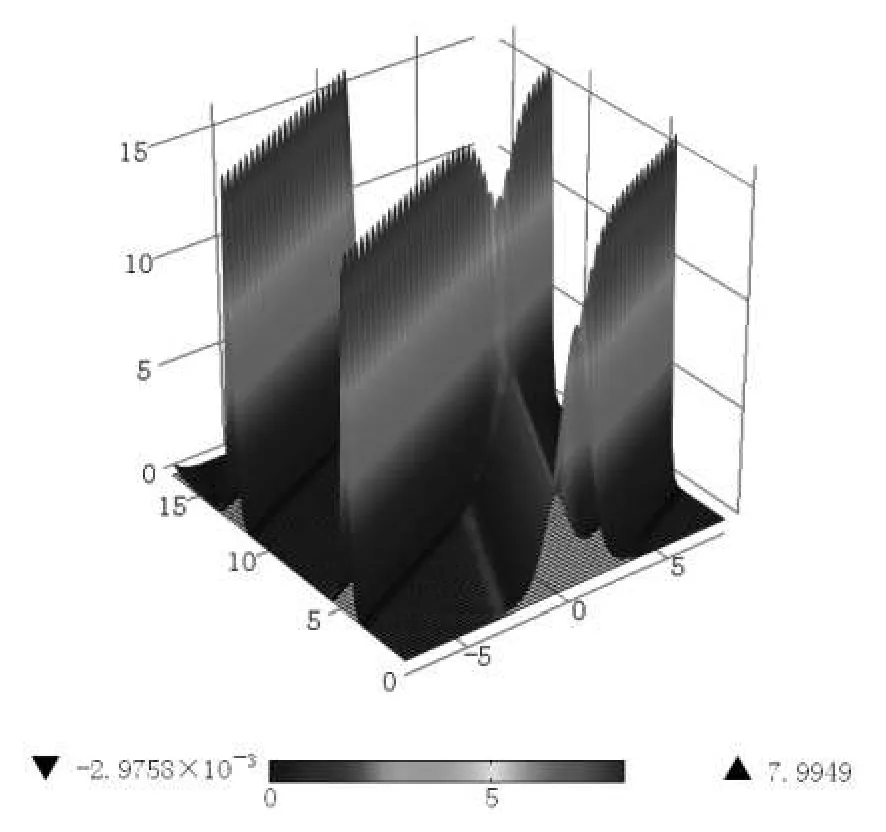
图4 孤立波波形在所有时刻的三维表示

3 结论

本文针对一类三阶KdV方程通过基于有限元法的COM⁃SOL Multiphysics软件进行求解，从数值计算结果可仿真模拟出孤立波的传播特性.有限单元法在求解偏微分方程中已有广泛的应用，传统方法都是建立数学模型进行精确求解，计算量大而且比较复杂.相比之下采用有限元法进行数值求解可以在很大程度上提高科研的效率，节省大量的人力、物力.对于高阶偏微分方程在COMSOL Multiphysics软件中很容易通过变量代换进行降阶的方式来求解.通过对孤立波的数值模型仿真分析证实本文的数值模拟方法是有效的.

图5 孤立波在时间t=0.0 s、0.4 s的分布

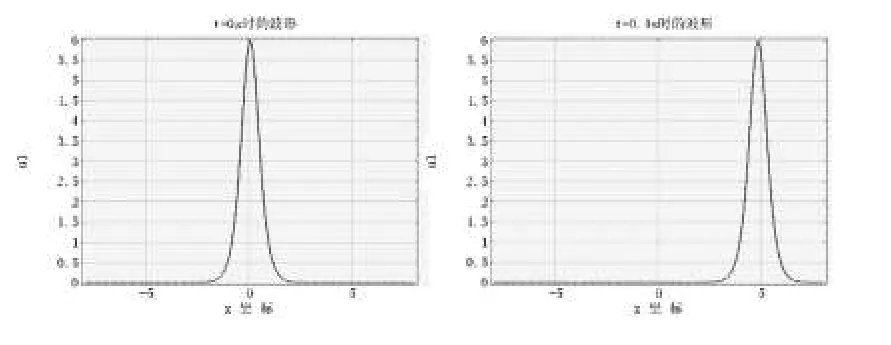
图6 孤立波在时间t=0.0 s、0.4 s的分布

[1]刘兴霞，孙建安.四次样条Galerkin有限元法求解KdV方程[J].西北师范大学学报，2008，44（4）：66-70.

[2]岳萍，龚伦训.用射影法求解KdV方程[J].大学物理，2010，29（2）：14-16.

[3]Otwinow ski M,Paul R,Laidlaw W G.Exact tavelling wave solutions o f a class of nonlinear diffusion equations by reduction to a quadrature[J].Phys Lett,1988,A128:483.

[4]杨红娟，石玉仁.用同伦分析法求解KdV方程的孤立波解[J].西北师范大学学报，2009，45（5）：39-43.

[5]钱天虹，刘中飞.双Jacobi椭圆函数展开法及其对KdV方程求解[J].安徽教育学院学报，2004，22（3）：5-8.

[6]Fan E G,Zhang H Q.The homogeneo us balance method for solving nonlinear soliton equations[J].Acta Phys Sin,1998,47(3):53.

[7]Kudry ashow N A.Ex act so lutions of the generalized Kuramo to Sivashinsky equation[J].Phys Lett,1990,A 147:287.

[8]William B J,Zimmerman，中仿科技公司.COMSOL Multiphysics有限元法多物理场建模与分析[M].北京：人民交通出版社.