第二型广义曲线积分

胡美蓉，戴培良

（常熟理工学院 数学与统计学院，江苏 常熟 215500）

纵观中外，许多数学家、数学学者历来都十分重视曲线积分的研究.文献[1]着重讨论了第一型曲线积分和第二型曲线积分在曲线为有限长和被积函数为有界函数这两种情况；文献[2]中则介绍了曲线长度计算定理及其证明.文献[3]探究了曲线为无穷长度曲线的第二型曲线积分的定义、性质、计算方法和收敛性判别；文献[4]则特别阐明了被积函数为无界函数的第二型广义曲线积分的定义、计算方法及收敛性；文献[5]着重讨论了被积函数不是连续函数的几个具体例子，阐述了这时计算曲线积分的方法.这些文献没有将有界闭围区域上的第二型曲线积分与被积函数为有瑕点的函数的曲线积分联系起来讨论，这为本文的研究提供了广阔的空间.

本文将进一步研究第二型广义曲线积分的定义、性质和计算方法，给出广义格林公式的具体内容并做出证明.

1 无穷曲线的第二型曲线积分

计算方法：平面无穷曲线 其中 x =φ(t)，y=ψ(t)在 [ α,+∞)上具有一阶连续导数，且 L 上任意两点 A 、 B 的坐标分别为 ( φ(α),ψ(α))、(φ(β),ψ(β))，又设函数 P (x,y)、Q(x,y)为 L 上的连续函数，则沿 L 从 A 到B的第二型广义曲线积分，若

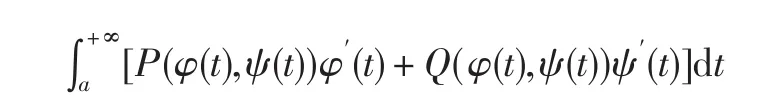
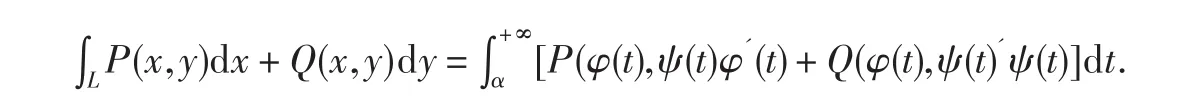
2 无界函数的第二型曲线积分

[3]中介绍了关于瑕点的定义，在此将根据瑕点所在的位置给出无界函数的第二型广义曲线积分的相关定义.为方便叙述，将点 A 为起点、点B为终点的有向曲线L记为L(AB)，并给出与瑕点位置有关的无界函数的第二型曲线积分的相关定义.

定义2 设L(AB)为 x oy平面上的一条光滑有向曲线，C为L(AB)上的任意一点（C≠B），二元函数P(x,y)和Q(x,y)在弧L(AC)上有界且可积，B为其瑕点，如果存在极限，则称此极限为无界函数P(x,y)在弧L(AB)上的关于x的第二型广义曲线积分，同理可给出Q(x,y)在L(AB)上的关于y的第二型广义曲线积分，并分别记为∫L(AB)P(x,y)dx=J1和∫L(AB)Q(x,y)dy=J2.我们把这个定义称为瑕点在曲线的一个端点时的第二型广义曲线积分.

定义3 设L(AB)为xoy平面上的一条光滑有向曲线，D为L(AB)上的一点且D点为瑕点（D≠A,B），C点为L(AD)上除端点外的任意一点，E点为L(DB)上除端点外的任意一点，若极限

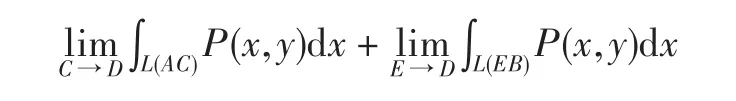
存在，则定义第二型广义曲线积分收敛，且

其中函数 P(x,y)在曲线段 L(AB)除 D点外有界可积，在 D的任一邻域内无界，但在 L(AC)⊂L(AD)及L(EB)⊂L(DB)都可积，我们把这个积分称为瑕点在曲线上（除端点外）的第二型广义曲线积分.

定义4 平面上有一光滑或逐段光滑的曲线L，函数P(x,y)和Q(x,y)以曲线L的两个端点为瑕点，且函数在任意曲线段L(CD)⊂L(AB)上可积，若极限存在，则此时第二型广义曲线积分收敛，这时定义瑕积分

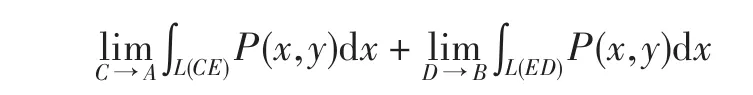
其中E为L(AB)上任意一点，我们把这个定积分称为瑕点在曲线两个端点时的第二型广义曲线分.

针对上述瑕点位置的定义，具有如下性质.

性质1（线性性质）：设L(AB)为平面有向可求长度的光滑曲线段，P(x,y)为平面上的一函数且在L(AC)上有界（C≠B），其中 B为瑕点，若无界函数第二型广义曲线积分 ∫L(AB)Pi(x,y)dx(i=1,2,3,…,n)存在，ki(i=1,2,3,…,n)为常数，则 也 存在，且有

以下两个性质均以曲线端点为被积函数的瑕点，且所给出的无界函数的第二型曲线积分收敛.

性质2（方向性）：设L(AB)为平面xoy上的一可求长度的光滑曲线，则其上的无界函数的第二型曲线积分与曲线 L (AB)的方向有关，即：∫L(AB)P(x,y)dx=-∫L(BA)P(x,y)dx.

性质3（可加性）：若光滑可求长度的曲线 L(AB)，且 L(AB)=L(AC)+L(CB)，第二型曲线积分∫L(AC)P(x,y)dx与 无 界 函 数 第 二 型 曲 线 积 分 ∫L(CB)P(x,y)dx存 在 ，则 有 ∫L(AB)P(x,y)dx也 存 在 ，且 有∫L(AB)P(x,y)dx= ∫L(AC)P(x,y)dx+ ∫L(CB)P(x,y)dx.

针对上述瑕点所在位置而给出的广义第二型曲线积分的定义，给出其计算方法.

计算方法：平面 x oy上有一光滑或逐段光滑的曲线L(AB)，且其中 α ≤t≤ β ，且 α 对应点 A，β对应点B，函数 x=φ(t)和 y=ψ(t)在α≤t≤β上有连续的一阶连续导数，P(x,y)和Q(x,y)为平面上的两个连续函数，则

此为瑕点在曲线一端点时的第二型广义曲线积分的计算公式.

证明当瑕点为端点B时，C为曲线上除点A、B外任意一点，因为

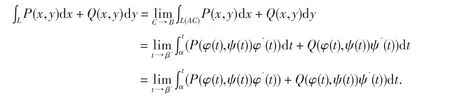
同理可证当瑕点为A点时的情况.

对于两端点 A,B均为瑕点的情形，可以在曲线L(AB)上除去两端点任取一点C，L(AB)=L(AC)+L(CB)，对L(AC)和L(CB)上的积分采用上述方法进行计算.

3 格林公式在无界函数的第二型广义曲线积分中的探究

本段主要讨论区域D的边界曲线L上无界函数的第二型广义曲线积分与曲线所围成的闭围区域D上的二重积分之间的联系，其中L为一条或几条光滑曲线组成，边界的正方向为人沿着边界行走时，区域D总在他的左边时的方向.

定理1 平面上曲线L为光滑或按段光滑的曲线，其围成的区域为D，平面上有两个函数P(x,y)和Q(x,y)，这两个函数在区域D内除点M(x0,y0)外都连续，且除点M(x0,y0)外都有连续的一阶偏导数，但在点M的邻域内无界；在点M的某去心领域内有（α为小于2的正常数）；当(x,y)→(x0,y0)即 r→0时，有 rP(x,y)→0，rQ(x,y)→0；则有

这里的L为区域D的边界曲线，并取正方向.公式（1）称为闭围区域上的广义格林公式.

证明由在区域D内除点M外处处有定义且都连续，在M的附近区域有其中α为小于2的正常数，相关的定理可知收敛[1].而 ∮LPdx+Qdy显然是收敛的.

如图1所示，因为区域D中的点M为函数P(x,y)、Q(x,y)和的瑕点，所以以点M为中心，r为半径画圆，圆所围成的区域设为Δ，Δ的边界曲线设为LΔ，在曲线上任取一点 A，LΔ上任取一点B，连接 A和B有

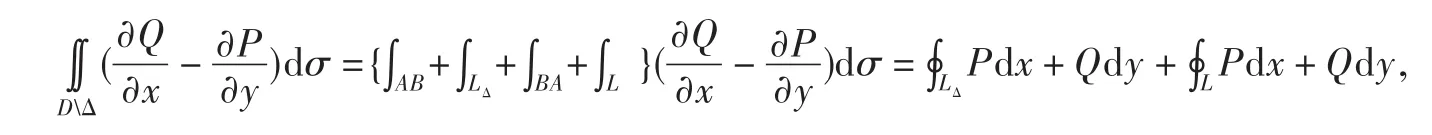
其中 Δ ={(x,y)*(x-x0)2+(y-y0)2≤r2}. 因 为 当( x ,y)→(x0,y0)，r→0 时 ，rP(x,y)→0，根据极限的定义有：对于任意的正数 ε ，总存在相应的正数 δ1，当M(x,y)∈ Uo(M0,δ1) 时，有 r P (x,y)-0<；同 理 当(x,y)→(x0,y0)，r→0时 ，rQ(x,y)→0；闭围区域Δ={(x,y)*(x-x0)2+(y-y0)2≤r2}的边界曲线用参数方程可表示为：

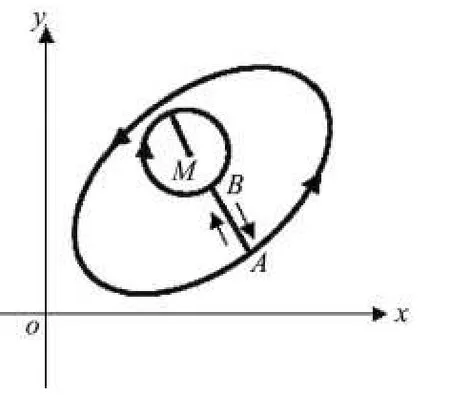
图1 平面关系图

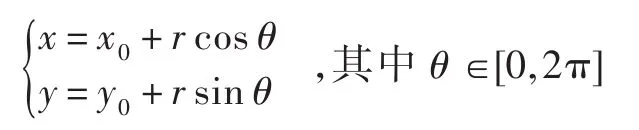
取 δ=min{δ1, δ2} ，当M (x,y)∈ Uo(M0,δ)时，有

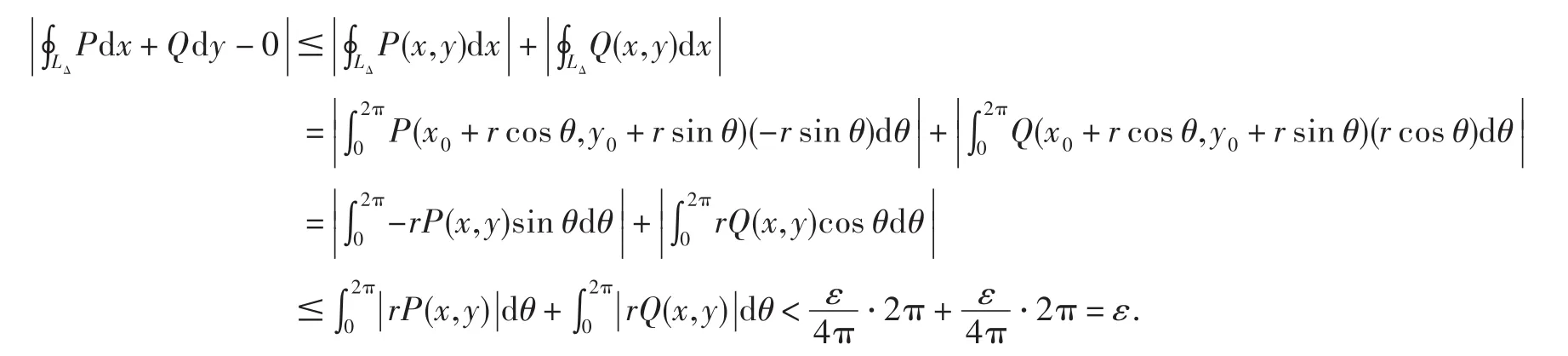
故

要求得区域D上的重积分，即使区域D上的重积分为0，也就是使区域的半径r无限接近0，根据上述分析则有

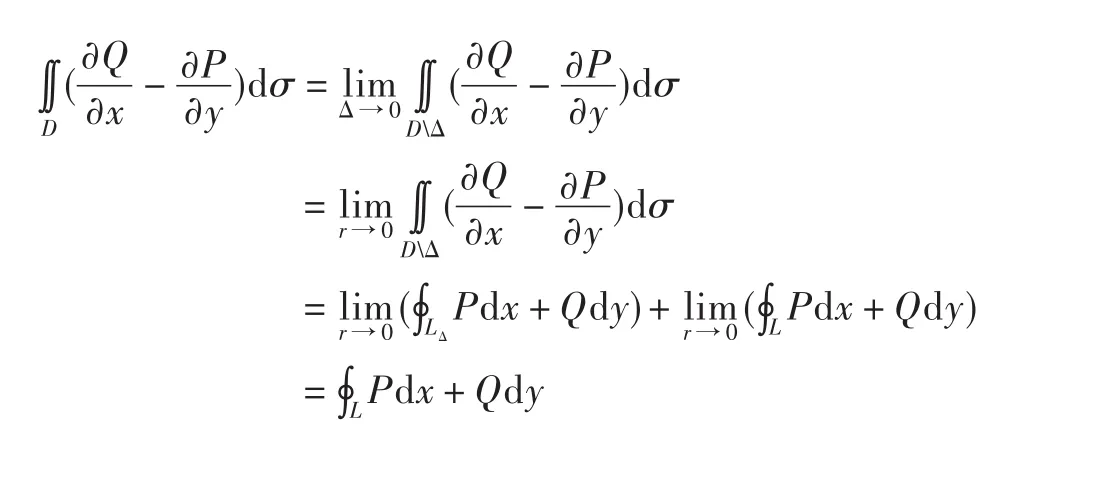
证毕.

参考文献：

[1]华东师范大学数学系.数学分析（下册）[M]3版.北京：高等教育出版社，2001：197-227.

[2]Г.И.阿黑波夫，В.А.萨多夫尼奇，В.Н.丘巴里阔夫.数学分析讲义[M]3版.昆扬，译.北京：高等教育出版社，2006：202-203.

[3]黄华，周道清.第二类广义曲线积分[J].重庆文理学院学报：自然科学版，2006，5（4）：57-59.

[4]齐春玲，任安忠.无界函数的第二类曲线积分[J].三门峡职业技术学院学报，2009，8（2）：105-107.

[5]姜洪文.对坐标的曲线积分的探讨[J].电大理工，2000（2）：10-12.