矩阵的中心化子及其维数
夏卫东,吴月柱
(常熟理工学院 数学与统计学院,江苏 常熟 215500)
1 引言
Mn(C)表示复数域C上所有n×n矩阵的全体.Mn(C)对数与矩阵的乘法及矩阵的乘法构成线性空间.
定义1.1 给定一个n阶方阵A,称C(A)={B ∈Mn(C)BA=AB} 为矩阵 A 的中心化子.
容易验证,C(A)是Mn(C)的一个子空间.本文将确定C(A),给出C(A)的基及维数.
矩阵的中心化子是有趣的问题,它不仅与古典矩阵对的相似标准形问题密切相关[1-3],而且在表示论中起着非常重要的作用.在文献[3]中,作者利用Weyr矩阵得到了矩阵中心化子的基底及其维数.本文将在第二节给出Jordan矩阵中心化子的基及维数,在第三节利用相似变换确定一般方阵的中心化子及其维数.
首先回忆Jordan块及Jordan矩阵的定义.
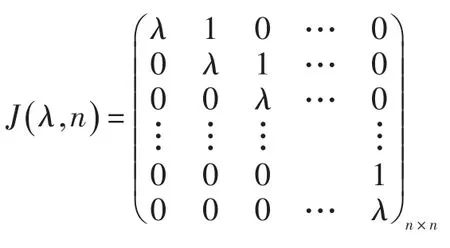
定义2.1 形如的矩阵称为Jordan块,其中λ是复数.
定义2.2 由若干个Jordan块组成的准对角矩阵称为Jordan矩阵,即形如的矩阵,其中为Jordan块.
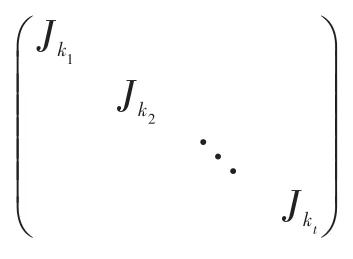
为确定Jordan矩阵的中心化子及其维数,需要下面的两个引理.
2 Jordan矩阵的中心化子及其维数
引理2.3 设Jn为n阶Jordan块,则

进而dim C(Jn)=n.
证明设 A=(aij)为与Jn交换的任意n阶方阵,即 A Jn=JnA.
计算可得
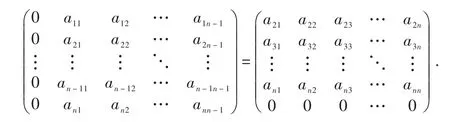
上式中对应的元素相等,可得:

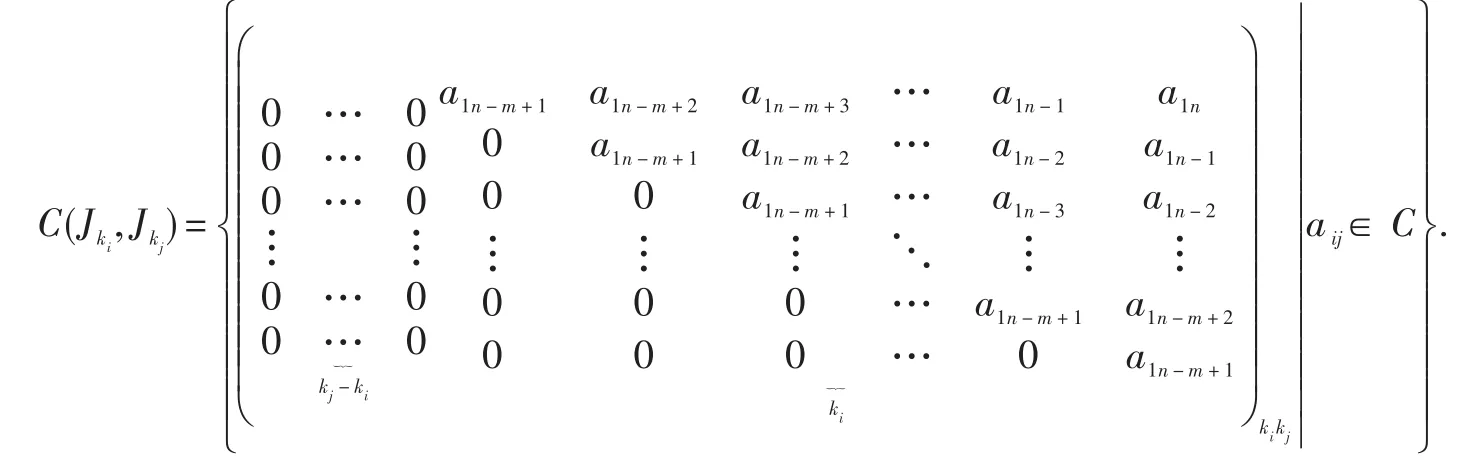
引理2.4 设Jn、Jm为两个Jordan块,A为m×n矩阵.令S={A-A Jn=JmA}. 则dim S=min{m ,n}.更确切地,
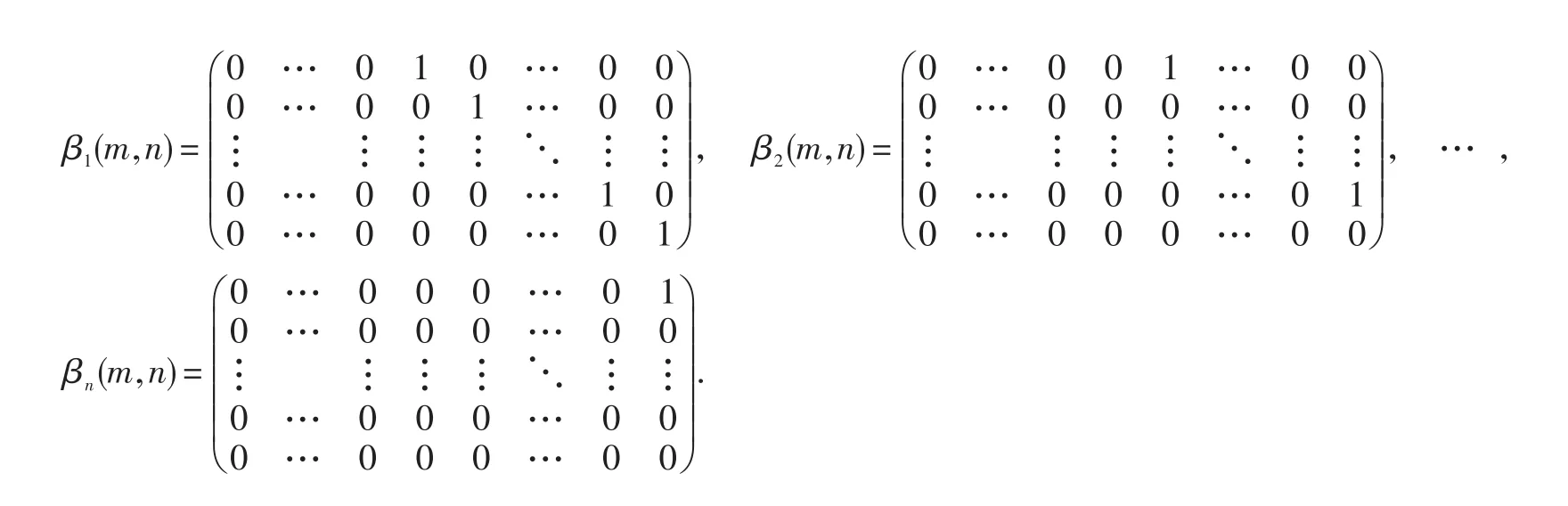
(1)若 m 进而dim S=m. (2)若 m>n,则 证明设A=()aijm×n为满足 A Jn=JmA 的矩阵 (1)当m 计算可得 上式中对应的元素相等,可得: 记 容易验证 β1(m,n),β2(m,n),…,βn(m,n)是S的一组基.所以dim S=m. (2)当m>n 时,由 Am×nJn=JmAm×n,可得 计算可得 上式中对应的元素相等,可得: 因此 记容易验证 γ1(m,n),γ2(m,n),…,γn(m,n)是S的一组基.所以dim S=n. 综上所述,dim S=min{m,n.} 定理2.5 设为Jordan矩阵.则 证明设与J交换.由 XJ=JX,得 即 上式中对应的子块相等,可得 下面分情况确定满足(*)式的Xij. 当i>j,此时 ki 当i 定义3.1 设 A ,B为n阶矩阵,如果存在n阶可逆矩阵P,使得P-1AP=B,则称 A 与B相似,记为A~B. 众所周知,复数域C上任一方阵A都与一个Jordan矩阵相似.本节将确定复数域上任意方阵的中心化子及其维数,为此需要下面的引理. 引理3.2 若 A,B相似,即存在可逆矩阵 P ,使得 P-1AP=B.则 P-1C(A) P=C(B).进而dim C(A)=dim C(B). 由上面的引理及定理2.5可得下面的定理. 定理3.3 设 A为复数域上任意n阶方阵.设 P为可逆矩阵满足 A=P-1JP,其中则 (1)C(A)=P-1C(J) P; [1]徐运阁,马晓静.矩阵对的相似标准形[J].大学数学,2008,24(1):104-107. [2]章超.矩阵中心化子[J].湖北大学学报:自然科学版,2009(4):325-328. [3]Sergeichuk V V.Canonical matrices for basic matrix problems[J].Linear algebra and its applications,2002,317(1-3):53-102.
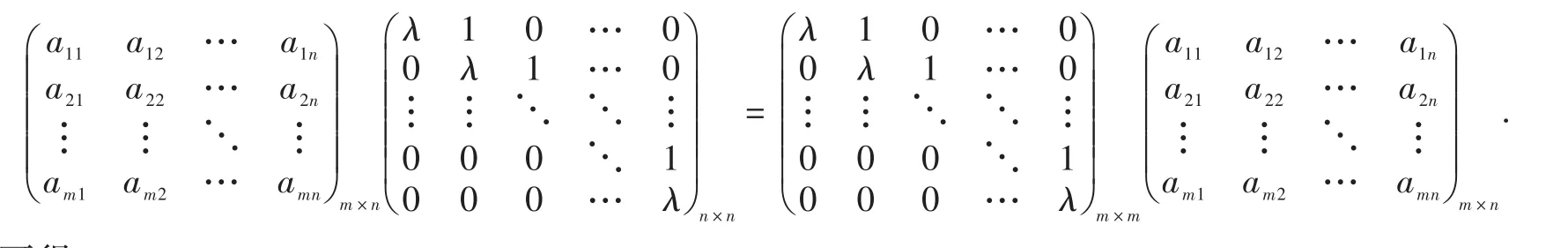
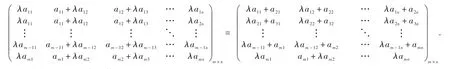



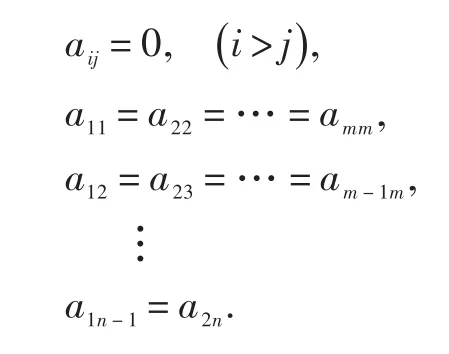
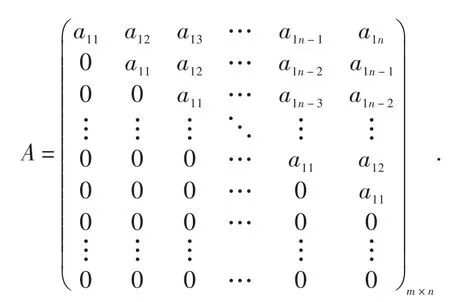

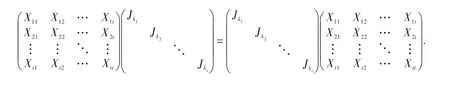


3 方阵的中心化子及其维数

