UHPC梁开裂弯矩和裂缝试验
徐海宾,邓宗才
UHPC梁开裂弯矩和裂缝试验
徐海宾1,2,邓宗才1
(1.北京工业大学工程抗震与结构诊治北京市重点实验室,100124北京;2.河南理工大学土木工程学院,454003河南焦作)
为研究超高性能混凝土梁的开裂弯矩和裂缝特征及评估现有规范公式计算超高性能混凝土梁开裂弯矩和裂缝宽度的适用性,进行了8根超高性能混凝土T形简支梁的受弯性能试验,观察试验梁的开裂弯矩和裂缝发展.试验结果表明:预应力水平对开裂荷载影响较大;超高性能混凝土梁的弯曲裂缝细而密,加载初期最大裂缝宽度发展较慢,纵筋屈服后最大裂缝宽度发展明显加快;利用现有规范公式计算超高性能混凝土梁开裂弯矩和最大裂缝宽度过于保守.在现行规范公式的基础上引入抗裂影响系数和裂缝修正系数,给出了超高性能混凝土梁开裂弯矩和最大裂缝宽度的建议公式,建议公式的计算值和试验值吻合良好.
超高性能混凝土;开裂弯矩;受弯性能;裂缝宽度;预应力
目前,超高性能混凝土(简称UHPC)因其卓越的力学性能和耐久性能受到越来越多的关注[1-2].为掌握UHPC梁的受力特性,国内外开展了一些试验并修建了一些示范桥,但对UHPC梁开裂弯矩和裂缝宽度的研究鲜见报道[3-5]. HRB500级钢筋是一种强度高、延性好的热轧带肋钢筋[6-8],将其与普通混凝土配合使用,存在正常使用极限状态下裂缝宽度超过规范限值的问题;若通过增加配筋率来限值裂缝宽度则失去了采用高强钢筋的意义,在一定程度上制约了高强钢筋的推广应用[6,7,9].将HRB500与UHPC配合使用,可以充分发挥两者的优越性能,然而目前相关研究鲜见报道.
本文进行了8根UHPC梁的受弯试验研究(其中6根梁中非预应力纵筋为HRB500级钢筋),研究了UHPC梁的抗弯性能,主要确定了在正常使用极限状态下梁的裂缝发展,提出了适合计算UHPC梁的开裂荷载及裂缝宽度的计算公式.
1 试验概况
1.1 试件设计
制备UHPC原材料如下:P.O52.5超细水泥,比表面积650 m2/kg;P.O42.5水泥,比表面积360 m2/kg;S95级粒化高炉矿渣,比表面积408 m2/kg;粒径40~70目的天然石英砂;高效聚羧酸类减水剂;直径0.12 mm、长8 mm的I型平直镀铜钢纤维;直径0.21 mm、长13 mm的II型端钩镀铜钢纤维.UHPC各组分质量比为,超细水泥:普通水泥∶矿渣∶石英砂∶高效减水剂∶I型钢纤维∶II型钢纤维=1∶2∶2∶4.544∶0.097 7∶0.858∶0.17∶0.34.
共制作8根T形截面试验梁,梁截面尺寸为:高350 mm,腹板厚120 mm,翼缘宽300 mm,翼缘厚50 mm.
梁主要变化参数为:纵筋类型、纵筋配筋率、预应力度PPR、张拉控制应力σcon.预应力筋采用φs15.2低松弛1860钢绞线,沿梁长水平直线布置,箍筋采用直径8 mm的HRB335钢筋,箍筋间距30 cm;2根非预应力梁未配置箍筋.试验梁具体参数见表1.
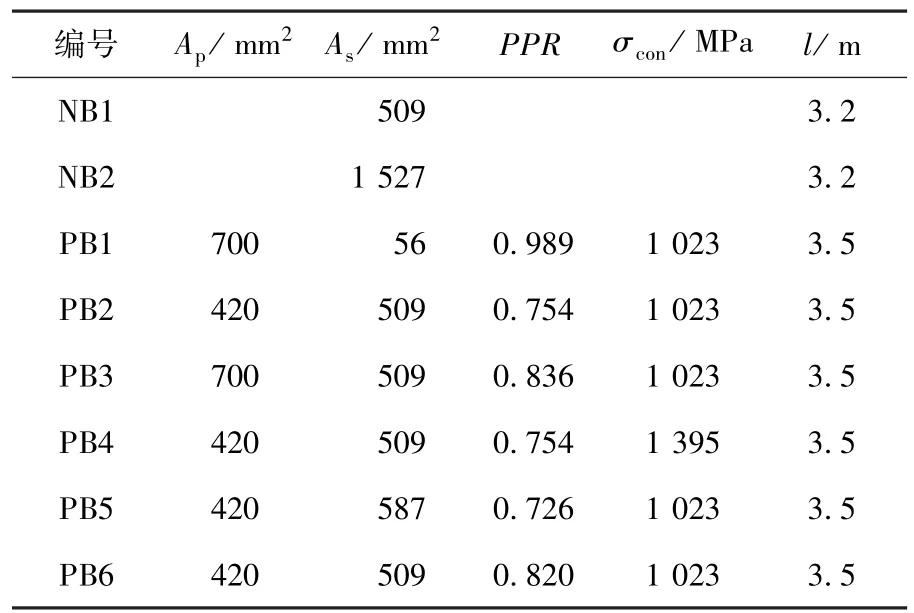
表1 试件参数
1.2 加载装置
加载装置见图1,在梁中部形成一个1 m长的纯弯段,以便研究纯弯段的裂缝性能.
1.3 测试设备及内容
试验加载采用300 t电液伺服控制系统,数据采集采用IMP35951B应变测试系统,裂缝宽度测量采用SW-LW-101型裂缝宽度观测仪.试验量测内容有:荷载、跨中区段纵筋应变与钢绞线应变增量、跨中截面混凝土应变、支座、跨中和两加载点处挠度、各级荷载下裂缝宽度.

图1 试验加载装置
1.4 材料力学性能
1.4.1 UHPC力学性能
根据与试验梁同时浇筑同条件养护的小试块测定的UHPC立方体抗压强度fcu、轴心抗压强度fc、轴心抗拉强度ft、弹性模量Ec见表2.
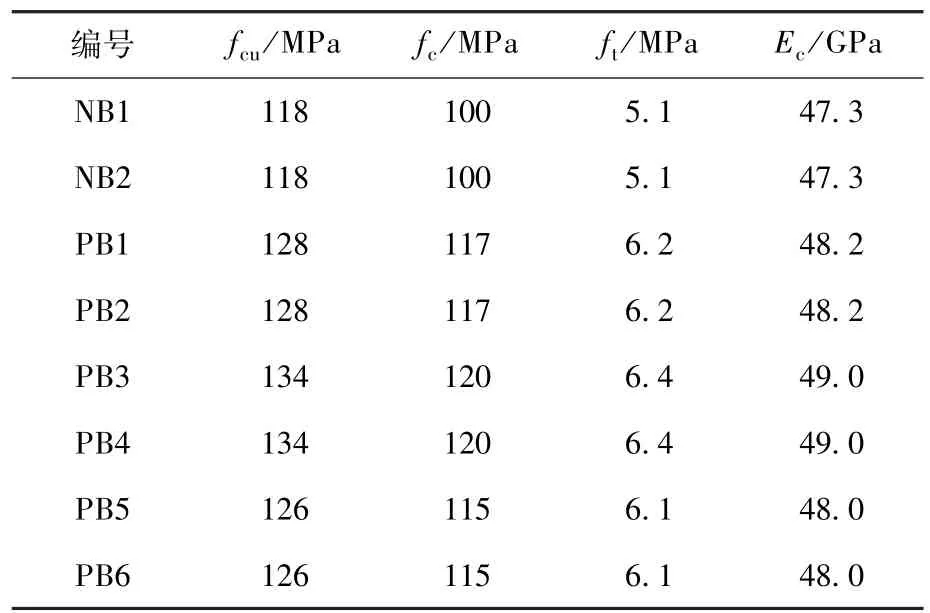
表2 UHPC力学性能
根据文献[3],UHPC的轴拉应力-应变见图2,极限拉应变εtu取0.007.
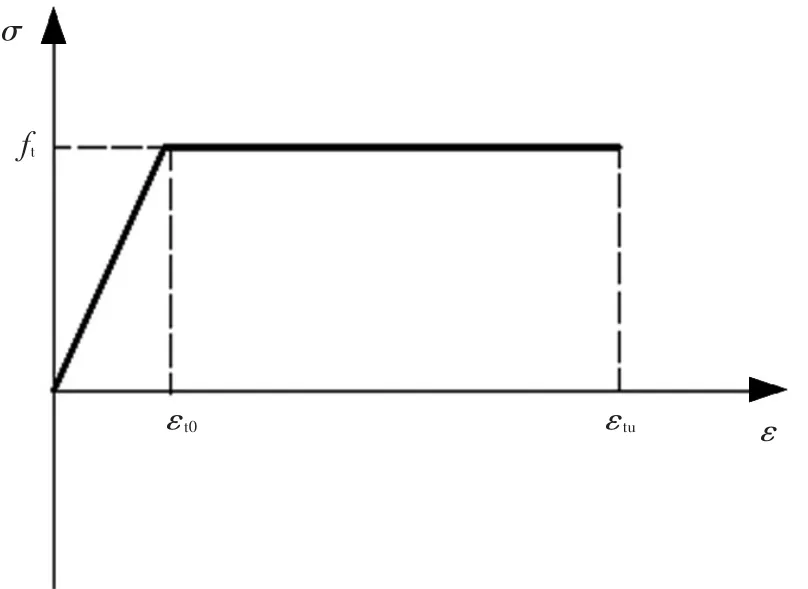
图2 UHPC轴拉应力-应变曲线
1.4.2 钢筋力学性能
试验采用HRB500钢筋分为直径16 mm和18 mm两种,实测屈服强度分别为521 MPa和536 MPa.HRB335钢筋直径18 mm,实测屈服强度380 MPa.
1.4.3 钢绞线力学性能
试验钢绞线实测名义屈服强度1 791 MPa、极限强度1 928 MPa、弹性模量193 GPa.
1.5 有效预应力
根据文献[3],计算UHPC构件收缩徐变引起的预应力损失时,可取收缩应变350×10-6,徐变系数0.2进行计算;其他原因引起的预应力损失依据JTG D62—2004《公路钢筋混凝土及预应力混凝土桥涵设计规范》[10]的相关条款进行计算,各梁有效预应力计算结果见表3.

表3 各梁有效预应力σpeMPa
2 试验结果与分析
2.1 试验过程及裂缝发展
图3为试件荷载-跨中挠度曲线,为清晰显示,除PB1外,其他梁的曲线较前一曲线均沿横坐标正向平移5 mm.图4为最终破坏阶段裂缝分布图.

图3 荷载-跨中挠度曲线

图4 试验梁裂缝分布
NB1和NB2为非预应力梁,达到开裂荷载时,加载点附近首先出现1~3条裂缝,荷载-挠度曲线出现首次明显转折;之后随着荷载的增加,裂缝数量和长度不断增加,NB1在接近屈服荷载时纯弯段形成3条较宽主裂缝,之后裂缝宽度快速增大,裂缝条数增加不多,达到屈服荷载时,荷载-挠度曲线出现第二次明显转折,之后荷载略有增加,挠度持续快速增大,试验梁破坏;NB2则在荷载达282 kN时,两加载点外侧出现指向加载点的斜裂缝;最终在荷载达512 kN时,左侧加载点外侧出现一条较宽斜向贯通裂缝,梁发生斜拉破坏.
6根预应力梁表现出典型的4阶段,即弹性阶段、裂缝开展阶段、屈服强化阶段、破坏阶段.弹性阶段,荷载与挠度基本成比例增长;开裂至纵筋屈服为裂缝发展阶段,随荷载增加,裂缝数量、长度、宽度均随之增加;纵筋接近屈服时,梁内形成3~5条较宽主裂缝,之后主裂缝宽度快速增加,纯弯段裂缝数量增加不多,弯剪段出现斜裂缝;当纵筋应力达到屈服应力时,荷载-挠度曲线出现第二次转折点,该阶段荷载-挠度曲线依然近似为直线;纵筋屈服至极限荷载段为屈服强化阶段,纵筋屈服后,由于钢绞线尚未屈服,受压区混凝土没有压碎,因此荷载继续增大,该阶段主裂缝长度和宽度增长较快,荷载-挠度曲线的斜率持续减小;极限荷载之后为破坏阶段,该阶段荷载下降,挠度快速增长,试验梁破坏.
2.2 裂缝影响因素分析
影响裂缝发展的因素较多,影响程度也有较大差异,下面分别就纵筋配筋率、纵筋强度等级、预应力水平、钢纤维对最大裂缝宽度和裂缝间距的影响加以探讨.
由于PB1中只配置了2根直径6 mm的光圆架立钢筋,加之构件采用后张法扁锚预应力体系,预应力钢筋布置位置靠梁底缘较远,因此钢筋对梁底缘混凝土应力分布帮助不大,造成裂缝间距及最大裂缝宽度均较大,裂缝宽度发展较其他梁发展快.由图5所示实测跨中弯矩-最大裂缝宽度曲线可知,纵筋屈服前,最大裂缝宽度随纵筋应力近似线性增长,纵筋屈服后,最大裂缝宽度增速明显加快,因此提高纵筋配筋率,增加构件的屈服弯矩,可以有效延缓裂缝宽度的发展.
PB2和PB6配筋面积完全相同,所不同在于所配纵筋类型分别为HRB500和HRB335钢筋.从裂缝分布图4可知PB2梁主裂缝间距比PB6更密集,且次生裂缝也更多.由图5可知,非预应力纵筋屈服前相同荷载下PB2和PB6的最大裂缝宽度基本相当,但由于HRB335纵筋屈服强度较低,因此HRB335钢筋屈服后PB6梁最大裂缝宽度迅速增大,而此时HRB500纵筋尚未屈服,其最大裂缝宽度增长缓慢.因此配筋相同时采用高强度等级钢筋可以有效延缓裂缝发展.
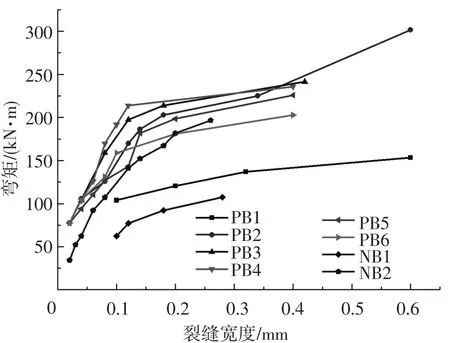
图5 弯矩-最大裂缝宽度曲线
从PB2、PB3、PB4、PB5实测最大裂缝宽度发展来看,预应力水平较高的PB3和PB4明显比预应力水平较低的PB2和PB5裂缝开展缓慢,0.6倍极限荷载时PB2、PB3、PB4、PB5对应的最大裂缝分别为0.13、0.08、0.10、0.13 mm,与各自的预应力水平相互对应.因此,提高梁的预应力水平,可以有效抑制裂缝的发展.
掺入钢纤维可有效抑制混凝土梁裂缝开展. UHPC中无粗骨料,且所用钢纤维直径小,钢纤维分布均匀,钢纤维与UHPC的粘结力较普通钢纤维混凝土更高.大量乱向分布的钢纤维一则能够降低基体中裂缝端部的应力集中从而延缓基体的开裂,二则跨越裂缝的钢纤维依靠与基体的较强粘结力承担裂缝截面上的部分拉应力,从而降低了裂缝截面处纵筋应力;三则钢纤维提高了纵筋与基体的粘结力,使纵筋的粘结滑移减小,裂缝间混凝土的平均拉应变提高,并产生众多细微裂缝,从而降低主裂缝宽度[11].因此提高钢纤维掺量、增强钢纤维与基体的粘结力对抑制裂缝开展具有显著的改善作用.
2.3 正截面开裂弯矩计算
计算开裂弯矩时需考虑受拉区混凝土塑性发展程度的影响,普通混凝土通常采用等效换算的方法,引入受拉区混凝土塑性影响系数γ的方法加以考虑.已有研究资料表明,影响γ的主要因素包括:截面尺寸、截面形状、配筋率及钢筋在截面中的位置、钢纤维掺量及钢纤维种类、预加力等[11].现行JTG D62—2004规范中γ及开裂弯矩计算公式分别为
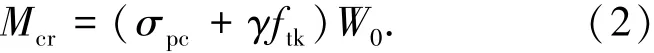
UHPC中由于钢纤维的桥联作用,其抗拉强度明显提高,且可延缓裂缝的萌生和扩展,受拉区UHPC塑性发展较普通混凝土更充分,受拉区塑性变形程度提高,开裂时的极限拉应变提高.钢纤维对受弯构件开裂弯矩的提高源于对钢纤维混凝土抗拉强度和塑性影响系数提高两方面的贡献.钢纤维对混凝土抗拉强度提高的贡献已经在开裂弯矩计算公式中得到体现,式(1)中也已经隐含了截面尺寸、截面形状、配筋率及配筋位置对γ的影响.因此,对超高性能混凝土,可在式(1)的基础上,引入抗裂影响系数β,用以考虑钢纤维对受拉区塑性发展程度提高的贡献,由此得:式中:β为抗裂影响系数,λf为钢纤维含量特征值,ρf为钢纤维体积率,lf为钢纤维长度,df为钢纤维直径或等效直径.
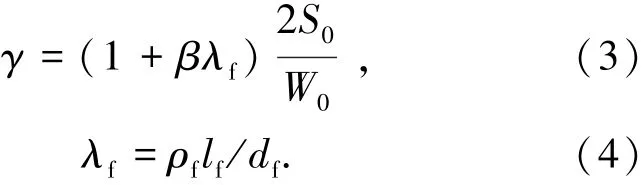
据试验数据及式(2)~(4)对抗裂影响系数β进行回归分析,回归得β=0.35,将β=0.35带入式(4)~(5)用于本文试验及文献[4]的计算,计算结果见表4.
由表4可知,计算值与试验值吻合良好,变异系数较小,可用于UHPC梁正截面开裂弯矩的计算.
2.4 裂缝宽度计算
结构设计时应对正常使用极限状态下结构的裂缝宽度加以限制,以免裂缝过宽影响结构的耐久性,造成结构承载力的下降和使用寿命的缩短.试验中偏保守的取0.6倍实测极限弯矩作为正常使用极限状态短期效应组合弯矩.试验中无法考虑长期效应的影响,因此对裂缝的长期发展不作讨论.
与普通混凝土相比,一则UHPC基体强度较高,远远超出规范中规定的最高强度C80;二则钢纤维对裂缝宽度开展具有较强的阻滞作用,因此不宜直接套用普通混凝土的裂缝宽度计算公式,但主裂缝间纵筋与混凝土的应变差决定裂缝宽度这一本质特征相同,因此可借鉴普通混凝土裂缝宽度的计算方法推求UHPC的裂缝宽度. GB50010—2010《混凝土结构设计规范》[12]提供的计算公式物理含义明确,方便理解,因此从GB50010—2010裂缝宽度计算公式出发,推求UHPC梁裂缝宽度的计算公式.GB50010—2010规定的在荷载标准组合或准永久组合并考虑长期作用影响的最大裂缝宽度计算公式为
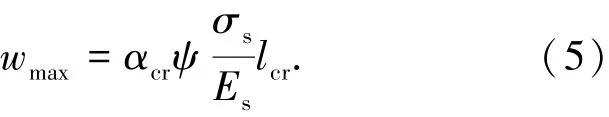
式中:αcr为构件受力特征系数,ψ为钢筋应变不均匀系数,σs为纵向受拉钢筋等效应力,lcr为平均裂缝间距.
下面通过分析UHPC与普通混凝土性能存在的差异,讨论GB50010—2010规范中各参数的变化规律.
1)纵筋应力.UHPC构件裂缝出现后,由于钢纤维的桥联作用,受拉区混凝土并不退出工作,而是可以协助纵筋承担部分拉力,随着裂缝的扩展和部分钢纤维的拔出,其所承担的拉力逐渐减小,因此,相比普通混凝土,UHPC中纵筋拉应力有所减小,但由于受拉区UHPC承担的拉力与裂缝宽度、钢纤维与混凝土粘结力、钢纤维数量及分布、钢纤维拔出量等有关,因此较难精确计算.8根试验梁的实测纵筋应力与依据GB50010—2010计算的钢筋应力比值的平均值为0.987,实测值较规范值偏小,但偏差不大.
2)平均裂缝间距.GB50010—2010中计算受弯构件平均裂缝间距的公式为
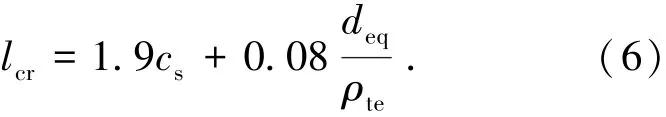
表5为按式(6)计算的平均裂缝间距与实测值的比较.表中lccr、ltcr分别为计算值和试验值.
鉴于梁NB2为斜拉破坏,因此表5中未统计.可见除PB1外平均裂缝间距的试验值均小于GB50010—2010计算值,而PB1中仅配置了2根φ6的光圆架立钢筋,且预应力钢筋位置距离梁下缘较远,对梁下缘裂缝开展抑制作用偏小,因此造成裂缝间距较大.分析其他梁平均裂缝间距较GB50010—2010计算值偏小的原因,由式(6)可知平均裂缝间距随纵向受拉钢筋配筋率ρte增大而减小,考虑UHPC中钢纤维的作用,实际上相当于增大了纵向受拉钢筋配筋率,而式(6)并未考虑该方面的影响.另外式(6)适用对象为普通混凝土,而UHPC一则强度较普通混凝土高出很多,二则不含粗骨料,内部缺陷较少,三则乱向分布的钢纤维具有抑制裂缝产生和限制裂缝扩展的作用,因此对UHPC的平均裂缝间距的计算,应考虑钢纤维的作用,对式(6)加以修正.

表5 平均裂缝间距计算值与试验值比较
3)钢筋应变不均匀系数.钢筋应变不均匀系数ψ是裂缝间钢筋平均应变与裂缝截面钢筋最大应变的比值.UHPC中钢纤维的桥联作用可以减小裂缝处钢筋的最大应变,但同时钢纤维也增加了钢筋与混凝土的粘结强度,从而导致钢筋平均应变减小,两者作用的结果互相抵消,对ψ的影响不大.8根试验梁实测ψ值与规范计算值比值的平均值为0.965,实测值比规范计算值略小.
4)构件受力特征系数.构件受力特征系数为

式中:τl为长期效应系数,此处不讨论;τs为最大裂缝宽度与平均裂缝宽度的比值,取1.66;αc为受拉混凝土平均应变影响系数,规范取0.77.
αc=1-εcm/εsm,其中εcm为裂缝间混凝土平均拉应变,εsm为裂缝间钢筋平均应变.UHPC中由于钢纤维的掺入使得钢筋与混凝土的粘结性能提高,裂缝间UHPC的平均拉应变提高,钢筋平均应变降低[11],因此系数αc应较GB50010—2010规范值偏小.
综合以上分析可知,利用GB50010—2010规范公式计算UHPC裂缝时,公式中各参数均应做适当调整,由于各参数主要受钢纤维类型、掺量、长径比等因素影响,且难以准确计算对各参数的影响程度,因此可以综合考虑钢纤维类型、掺量、长径比等对各参数的整体影响,对GB50010—2010规范公式加以修正:
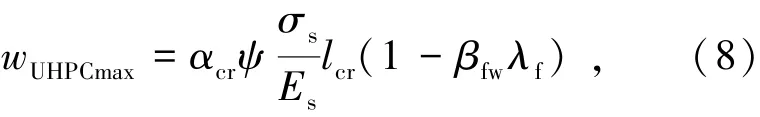
式中βfw为裂缝修正系数.
根据试验实测数据及公式(8)对裂缝修正系数βfw进行回归分析,结果见表6.表中为规范计算短期最大裂缝宽度,为试验实测最大裂缝宽度.

表6 裂缝修正系数
由表6可知,各梁回归所得裂缝修正系数βfw介于0.38~0.54,平均值为0.47,变异系数0.11,具有较高的可信度.出于保守考虑,可取βfw= 0.35,使得裂缝最大宽度计算值大于实测值,以便增加安全储备.
3 结 论
1)UHPC梁裂缝间距较普通混凝土梁密集,尤其是具有较多的次生裂缝;纵筋屈服前最大裂缝宽度随纵筋应力增加而近似线性增长,纵筋屈服后最大裂缝宽度快速增大,适当提高纵筋配筋率,可以有效控制正常使用阶段裂缝的最大宽度.
2)加大配筋率、采用高强度等级钢筋、提高预应力水平均有利于限制裂缝的发展.
3)由于钢纤维对受拉区混凝土塑性影响系数γ的提高作用,实测开裂弯矩比JTG D62—2004规范计算值偏大,通过引入抗裂影响系数β对γ加以修正后,可以较好的计算UHPC梁的开裂弯矩.
4)GB50010—2010裂缝计算公式可以反映UHPC梁裂缝规律,但计算结果过于保守.通过引入裂缝修正系数βfw,可以较好地对UHPC梁短期最大裂缝宽度进行计算.
5)试验中未考虑尺寸效应和长期效应对裂缝的影响,今后宜做进一步研究.
[1]徐海宾,邓宗才.超高性能混凝土在桥梁工程中的应用[J].世界桥梁,2012,40(3):63-67.
[2]STEINBERG E.Structure reliability of prestressed UHPC flexure models for bridge girders[J].Journal of Bridge Engineering,2010,15(1):65-72.
[3]GRAYBEAL B.Characterization of the behavior of ultrahigh performance concrete[D].Maryland:University of Maryland,2005.
[4]杨剑.CFRP预应力筋超高性能混凝土梁受力性能研究[D].长沙:湖南大学,2007.
[5]卢姗姗,郑文忠.GFRP筋活性粉末混凝土梁正截面抗裂度计算方法[J].哈尔滨工业大学学报,2010,42(4):536-540.
[6]易伟建,杨晓,李琼.HRB500级钢筋混凝土梁裂缝与变形性能试验研究[J].建筑结构,2011,41(8): 110-114.
[7]李志华,苏小卒,赵勇.配置高强钢筋的混凝土梁裂缝试验研究[J].重庆建筑大学学报,2010,32(1): 51-55.
[8]黄伟,张丽,吴明超.HRB500级钢筋混凝土梁受弯性能试验研究[J].工业建筑,2011,41(7):58-62.
[9]金伟良,陆春华,王海龙,等.500级高强钢筋混凝土梁裂缝宽度试验及计算方法探讨[J].土木工程学报,2011(3):16-23.
[10]JTG D62—2004公路钢筋混凝土及预应力混凝土桥涵设计规范[S].北京:人民交通出版社,2004.
[11]林涛,黄承逵.钢筋钢纤维高强混凝土梁正常使用极限状态研究[J].建筑结构,2006,36(4):81-83.
[12]GB50010—2010混凝土结构设计规范.[S].北京:中国建筑工业出版社,2010.
(编辑 赵丽莹)
Cracking moment and crack width of ultra-high performance concrete beams
XU Haibin1,2,DENG Zongcai1
(1.Beijing Key Lab of Earthquake Engineering and Structural Retrofit,Beijing University of Technology,100124 Beijing,China;2.School of Civil Engineering,Henan Polytechnic University,454003 Jiaozuo,Henan,China)
Eight ultra-high performance concrete T-beams subjected to bending were tested to investigate their cracking moments and cracking characteristics and evaluate the formulas for cracking moment and crack width specified in existing design codes.The test results show that the degree of prestress has a great impact on the cracking moment;the bending cracks are dense and fine,the development of the maximum crack width is slow at the early stage of loading and speeds up remarkably when the reinforcements reach to yield strength. Predicating the cracking moment and maximum crack width by existing code formulas will lead to overly conservative results.The modified formulas of cracking moment and crack width are suggested for ultra-high performance concrete beams by introducing the anti-cracking effect coefficient and crack-correction coefficient respectively,and the calculated values by the suggested formulas agree well with the test results.
ultra-high performance concrete;cracking moment;flexural behavior;crack width;prestress
TU375.1
A文章编号:0367-6234(2014)04-0087-06
��矩计算值与试验值比较
计算值/(kN·m)试验值/(kN·m)试验值/计算值NB135.132.80.93 NB237.935.30.93 PB1109.6106.71.03本文PB291.294.80.96 PB3108.5107.61.01 PB4109.6117.20.94 PB594.193.41.01 PB699.893.91.06 FB-65-R-S85.185.70.99文献[4]FB-00-R-S23.023.20.99 FB-45-R-S70.069.71.00 FB-45-R-S-NS71.368.41.04平均值0.99变异系数0.04
2013-08-06.
国家自然科学基金资助项目(50978006);教育部博士点基金资助项目(20131103110017).
徐海宾(1979—),男,讲师,博士研究生;
邓宗才(1961—),男,教授,博士生导师.
邓宗才,dengzc@bjut.edu.cn.

