内填部分混凝土箱形截面钢桥墩的延性影响参数

高圣彬，徐旻洋，张大旭（.上海交通大学船舶海洋与建筑工程学院土木工程系，0040上海；.上海现代设计（集团）有限公司技术中心，0004上海）

内填部分混凝土箱形截面钢桥墩的延性影响参数

高圣彬1，徐旻洋2，张大旭1
（1.上海交通大学船舶海洋与建筑工程学院土木工程系，200240上海；2.上海现代设计（集团）有限公司技术中心，200041上海）

为了研究内填部分混凝土箱形截面钢桥墩在恒定竖向荷载与柱顶水平往复荷载作用下的延性性能，建立三维弹塑性有限元模型，通过比较模拟结果与试验结果的水平荷载-水平位移滞回曲线和破坏模态，确定了所采用有限元分析方法的准确性与有效性.以翼缘宽厚比、柱长细比、混凝土填充率和柱轴压比为变化参数，建立56个三维弹塑性有限元分析模型，归纳总结了钢桥墩可能出现的各破坏模态:对于纯钢桥墩，局部屈曲发生在试件底部；对于内填部分混凝土钢桥墩，当混凝土填充率较小时，局部屈曲通常发生在内填混凝土上部钢板处；随着混凝土填充率的增大，局部屈曲出现在试件底部附近.最后分析上述4个参数对钢桥墩极限承载力和延性性能的影响规律.

内填部分混凝土钢桥墩；数值模拟；破坏模态；延性性能

钢管混凝土结构具有承载力高、塑性和韧性好、耗能能力强等优点，被广泛应用于土木工程领域［1-2］.为提高钢桥墩的抗震性能，日本学者［3-4］首先提出在钢桥墩内部填充部分混凝土的概念.在纯钢桥墩中填充混凝土，一方面可以提高其抵抗车辆撞击的能力，另一方面又可以提高其吸能能力并改善钢桥墩的延性.钢管混凝土桥墩分为全填充混凝土和部分填充混凝土两种类型，相比而言，部分填充混凝土钢桥墩具有如下优点：在安全性上，填充部分混凝土后的钢桥墩，自重较轻，降低了地基基础的负载；在经济性上，只填充部分混凝土，造价相对较低；在结构合理性上，在弯矩最大的桥墩根部附近填充混凝土，符合结构受力要求.

国内外学者对钢管混凝土结构的研究由来已久.日本学者［4-5］提出了混凝土最佳填充高度概念，认为评价混凝土最佳填充高度的标准为：在水平往复荷载作用下，中空部分钢板屈曲的同时，桥墩根部附近的混凝土刚好达到极限压应变，这样的混凝土填充高度即为最佳高度，所对应的混凝土填充率被称为最佳混凝土填充率.

王跃东等［6］在对部分填充混凝土钢桥墩进行试验研究的基础上，采用三维弹塑性有限元模型进行数值模拟.对于破坏发生在内填混凝土上方钢板的试件（当混凝土填充率较小时），模拟结果与试验吻合良好.对于破坏发生在底部的试件（当混凝土填充率较大时），由于混凝土严重压碎导致数值模拟发散，未能得出有效模拟结果.

日本学者Goto等［7-8］对内填部分混凝土圆形和箱形截面钢桥墩进行了数值模拟，采用基于分离裂缝模型的混凝土本构关系，成功模拟了混凝土填充率较大时的钢桥墩破坏.该分析模型需要人为指定较为薄弱的混凝土层，使得模拟过程中只允许在该处出现主裂缝，这种预设混凝土开裂位置的数值模拟方法带有较强的主观性，缺乏普遍适用性.

本文基于文献［6］的有限元建模方式，采用基于全应变理论的混凝土弥散裂缝模型，对破坏发生在底部的内填部分混凝土钢桥墩进行数值模拟.在与试验结果进行验证的基础上，建立56个三维弹塑性有限元分析模型，研究内填部分混凝土钢桥墩的破坏模态以及翼缘宽厚比、柱长细比、混凝土填充率、柱顶轴压比等4个参数对内填部分混凝土钢桥墩极限承载力和延性性能的影响规律.本文通过三维弹塑性有限元模拟所得钢桥墩试件的大量极限承载力和延性结果数据有望为后续开发应用于钢桥墩设计的二维梁单元简化模型提供非常宝贵的校核依据.

1 数值模拟方法的试验验证

1.1 有限元建模

图1为钢桥墩示意图，桥墩高度为h，混凝土填充高度为Lc．有限元模型中的单元选取、网格划分、边界条件、钢材本构关系、以及钢板与混凝土界面上的接触模型等与文献［6］基本相同，在此不再赘述.为了改善在高混凝土填充率下数值分析模型的收敛性，本文采用通用有限元软件DIANA［9］中的基于全应变理论的混凝土弥散裂缝模型，该模型首先由Vecchio等［10］提出，采用应力-全应变关系曲线描述混凝土受拉边与受压边的力学行为，与多方向混凝土固定裂缝模型相比，具有更好的数值稳定性.混凝土在受压时的应力-应变关系可以分为约束模型和非约束模型两种，混凝土约束模型的抗压强度高于非约束模型，且达到抗压强度后的曲线下降梯度缓慢.根据高圣彬等［11］对内填部分混凝土钢桥墩中的混凝土本构模型研究成果，本文采用图2所示“约束模型”曲线作为考虑钢板对内填混凝土约束效应后的混凝土应力-应变关系曲线.当混凝土压应变大于峰值应变εcc时，用下降直线来模拟混凝土受压边的应力软化特性．当压应变大于11εcc时，混凝土应力-应变关系变为水平直线［12］．

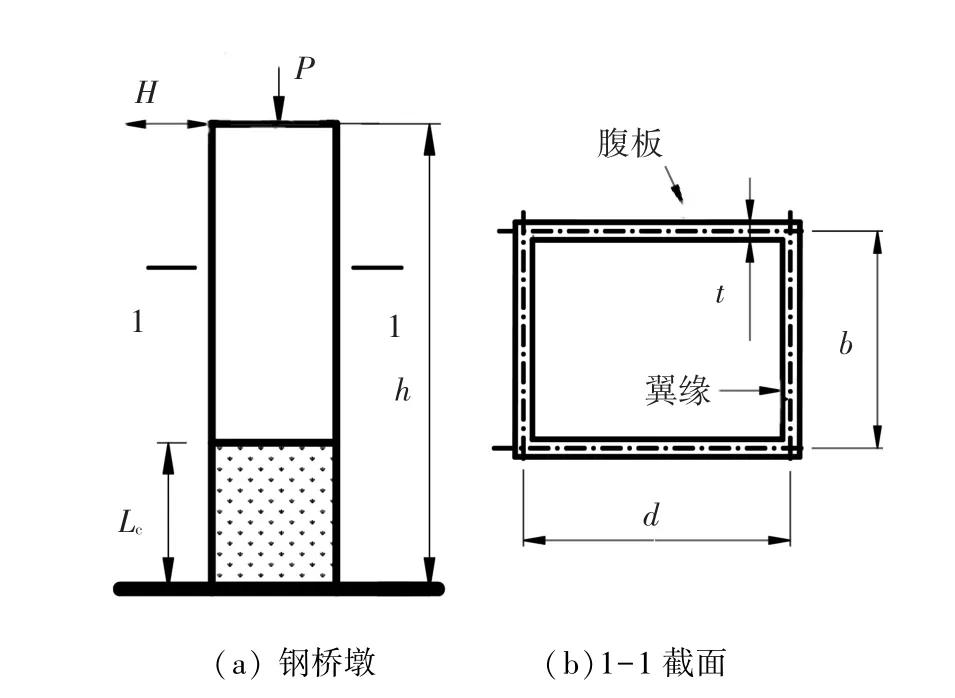
图1 钢桥墩示意

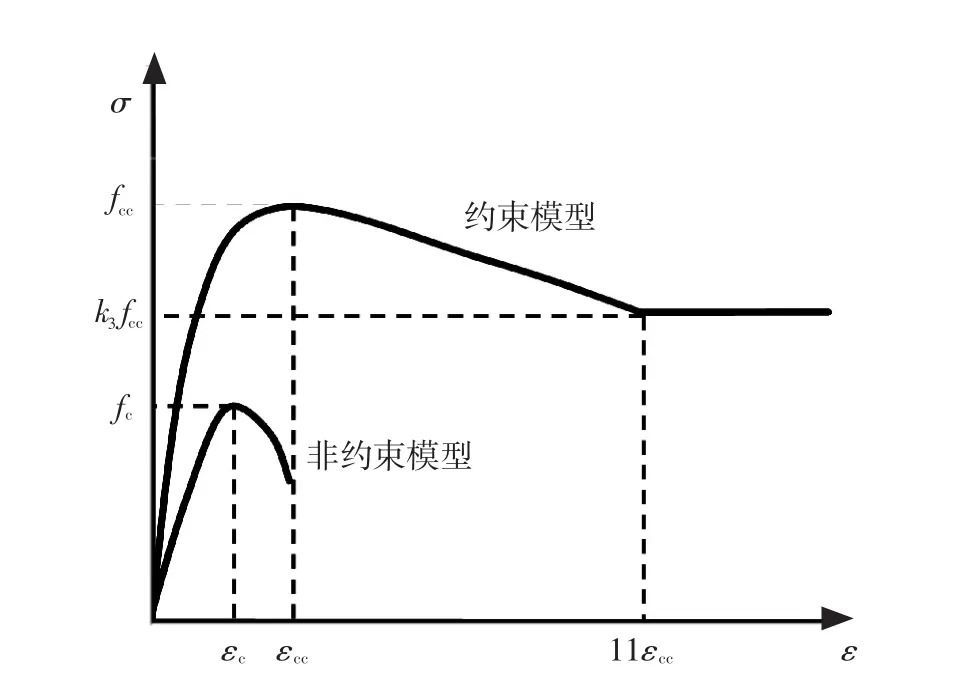
图2 混凝土单轴受压应力-应变关系

建立与试验试件几何属性完全相同的两个三维有限元分析模型，具体几何参数如表1所示.试件编号“S73-32-50”中，“73”表示翼缘宽厚比为0.73，“32”表示柱长细比为0.32，“50”表示混凝土填充率为试件高度的50%.其中，翼缘宽厚比Rf、柱长细比定义为

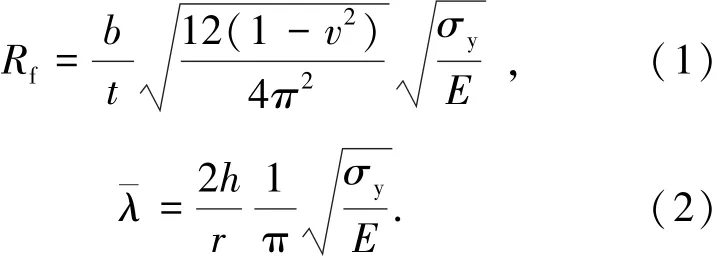
式中：b为翼缘板宽度，t为翼缘板厚度，σy为钢材屈服强度，E为钢材弹性模量，ν为钢材的泊松比，r为箱形截面回转半径．翼缘宽厚比参数控制钢板的局部屈曲，而柱长细比参数反映柱的整体稳定性大小．

表1 试件几何参数

1.2 计算结果与试验结果对比

1.2.1 水平荷载-水平位移滞回曲线比较

图3为有限元分析所得水平荷载-水平位移滞回曲线与试验结果的比较，其中纵轴和横轴分别采用考虑轴力影响的柱顶水平屈服荷载Hy和水平屈服位移δy进行无量纲处理．可以看出，模拟结果的初始刚度和最大荷载与试验结果吻合较好；最大荷载所对应的位移与试验结果有一些偏差，模拟结果的位移略小于试验结果；在达到最大荷载以后，模拟结果的荷载下降梯度与试验结果相比，相差不多，两者的下降段形状吻合较好．

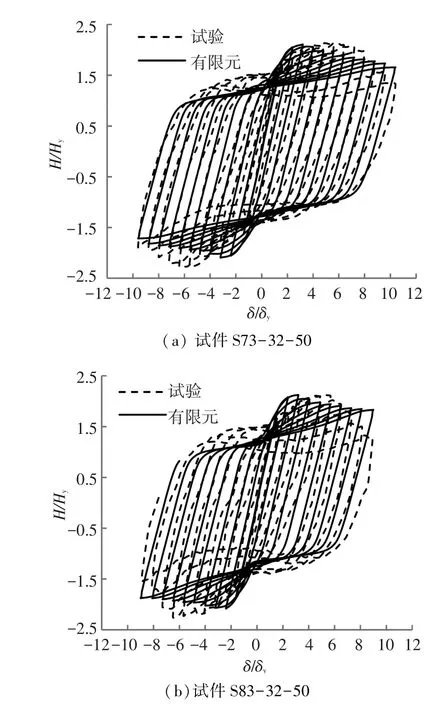
图3 水平荷载-水平位移滞回曲线比较

1.2.2 破坏模态比较

对于填充混凝土50%的试件S73-32-50和S83-32-50，钢板屈曲发生在试件底部附近，且由于内填混凝土对钢板的支撑作用，四周钢板均发生向外的鼓曲变形.图4为试件S73-32-50的有限元分析结果与试验结果比较，从破坏位置和破坏方式上看，有限元结果均与试验结果吻合较好.

图4 试件S73-32-50的破坏模态比较

综上所述，有限元分析所得滞回曲线、破坏模态与试验结果吻合较好，表明本文所建立的有限元分析模型可以有效模拟钢桥墩的滞回性能.

2 钢桥墩数值模拟与结果考察

以翼缘宽厚比、柱长细比、混凝土填充率和柱轴压比为变化参数，建立56个三维弹塑性有限元模型.试件编号“S60-40-50-1P”中，“1P”表示柱顶轴力为桥墩轴向屈服荷载的0.1倍，若无此项，则默认柱顶轴力为桥墩屈服荷载的0.2倍.

取试件达到最大荷载Hmax时对应的位移为荷载下降至Hmax的0.95倍处所对应的位移为试件的极限位移，延性系数μ为．各试件的有限元模拟结果见表2．

2.1 破坏模态分析

纯钢桥墩的破坏模态如图5（a）、（b）所示，破坏均发生在钢桥墩底部.图5（a）示翼缘处的钢板发生向外的凸起屈曲，而腹板处的钢板发生轻微向内的凹进屈曲；图5（b）所示翼缘处的钢板发生向内的凹进屈曲，而腹板处的钢板发生向外的凸起屈曲.

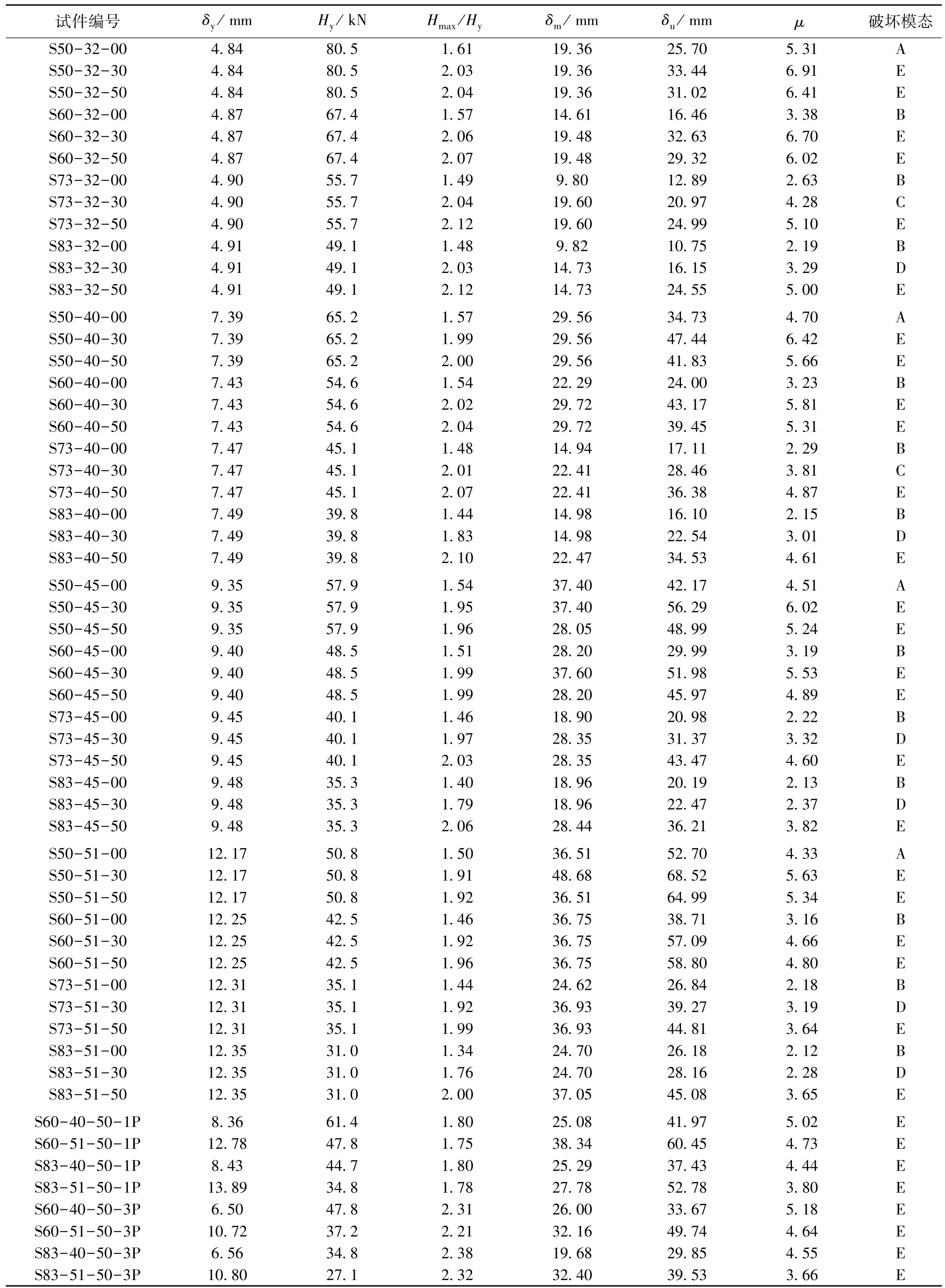
表2 有限元模拟结果

内填部分混凝土钢桥墩的破坏模态如图5（c）～（e）所示.图5（c）和图5（d）为混凝土填充高度小于最佳填充高度的情况，破坏发生在内填混凝土上方钢板处，底部弯矩较大部位的钢板并未屈曲，可见内填混凝土可以有效抑制底部钢板屈曲的产生.图5（e）为混凝土填充高度大于最佳填充高度的情况，钢板屈曲发生在试件底部，四周钢板出现向外的鼓曲变形.由此可见，虽然填充混凝土可以有效抑制钢板屈曲，使其位置发生变化，但内填混凝土达到最佳填充高度以后，钢板屈曲破坏仍发生在试件底部附近.

图6（a）、（b）是试件长细比分别为0.32和0.40时，钢桥墩5种破坏模态所对应荷载-位移滞回曲线的骨架曲线比较.由表2、图5和图6可以得出如下结论：

1）对于纯钢桥墩，破坏模态为试件底部钢板发生局部屈曲，分为底部钢板向外凸起屈曲和向内凹进屈曲两种模式.当翼缘宽厚比较小时（Rf= 0.50），破坏模态为底部钢板发生向外凸起屈曲．随着翼缘宽厚比的增大（Rf≥0.60），破坏模态转变为底部钢板发生向内凹进屈曲.发生向外凸起屈曲（S50-32-00、S50-40-00）时的延性性能优于发生向内凹进屈曲时（S60-32-00、S60-40-00）.

2）对于内填部分混凝土钢桥墩，当混凝土填充高度小于最佳填充高度时，破坏模态为内填混凝土上方钢板发生局部屈曲.其中，当翼缘宽厚比和柱长细比较小时，为向外凸起屈曲（S73-32-30、S73-40-30）.随着翼缘宽厚比和柱长细比增大，转变为向内凹进屈曲（S83-32-30、S83-40-30）.

3）当混凝土填充高度大于最佳填充高度（S83-32-50、S83-40-50）时，破坏模态为底部钢板发生向外鼓曲变形，该类桥墩有优越的延性性能.

4）对于破坏模态A和B以及C和D，虽然钢板发生局部屈曲的位置相同，但是屈曲方式不同.翼缘宽厚比和柱长细比越大的钢桥墩试件，越容易出现钢板向内凹进屈曲的破坏模态.

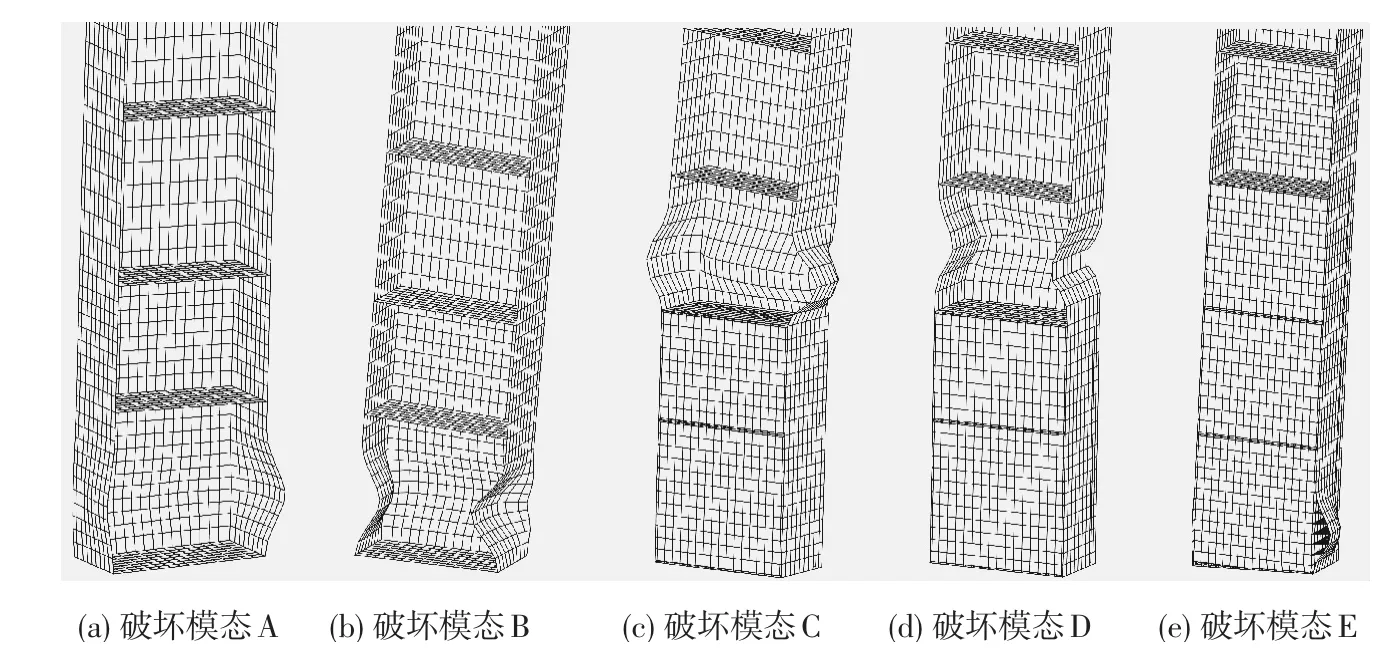
图5 钢桥墩破坏模态

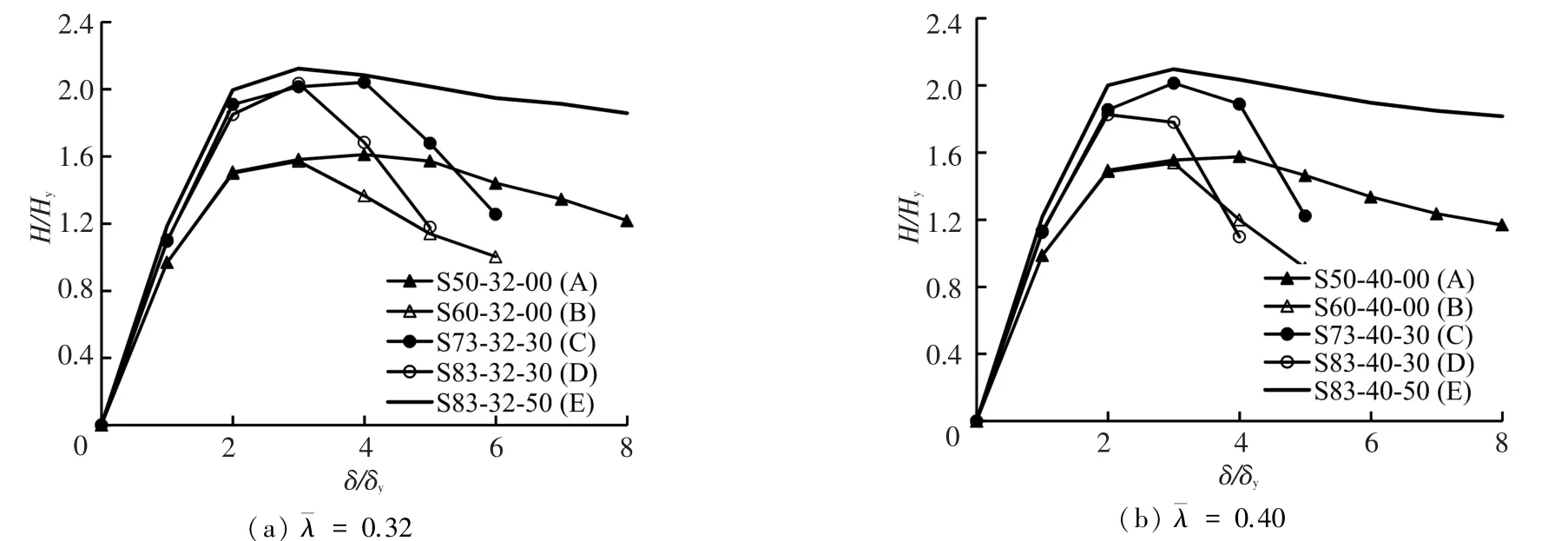
图6 各破坏模态所对应的荷载-位移骨架曲线比较

2.2 钢桥墩极限承载力和延性性能的参数影响分析

基于所建立的56个三维有限元分析模型，研究翼缘宽厚比、柱长细比、混凝土填充率和柱顶轴压比等4个参数对钢桥墩在承受恒定竖向荷载与水平往复荷载作用下的极限承载力和延性性能的影响，并各选取两张典型的水平荷载-水平位移滞回曲线的骨架曲线比较图来加以说明.

2.2.1 翼缘宽厚比影响

如图7（a）所示，对于混凝土填充率为30%的钢桥墩，翼缘宽厚比的增大将导致钢桥墩的极限承载力和延性性能降低.由于试件S50-45-30和试件S60-45-30的钢板破坏都出现在试件底部附近，它们的极限承载力和延性性能相差不大，且具有良好的延性性能.对于混凝土填充率为50%的钢桥墩（图7（b）），钢板破坏都出现在试件底部附近，翼缘宽厚比的变化对其极限承载力和延性性能影响很小.

2.2.2 柱长细比影响

图8是翼缘宽厚比分别为0.83和0.60时的柱长细比影响比较.当混凝土填充率为30%时（图8（a）），破坏模态为内填混凝土上方钢板出现局部屈曲，此时柱长细比的影响比较显著.图8（b）是混凝土填充率为50%的情况，破坏模态都是底部附近钢板出现局部屈曲，此时柱长细比的影响比较小.无论混凝土填充率为30%或50%，柱长细比的增大均导致钢桥墩极限承载力和延性性能的降低.

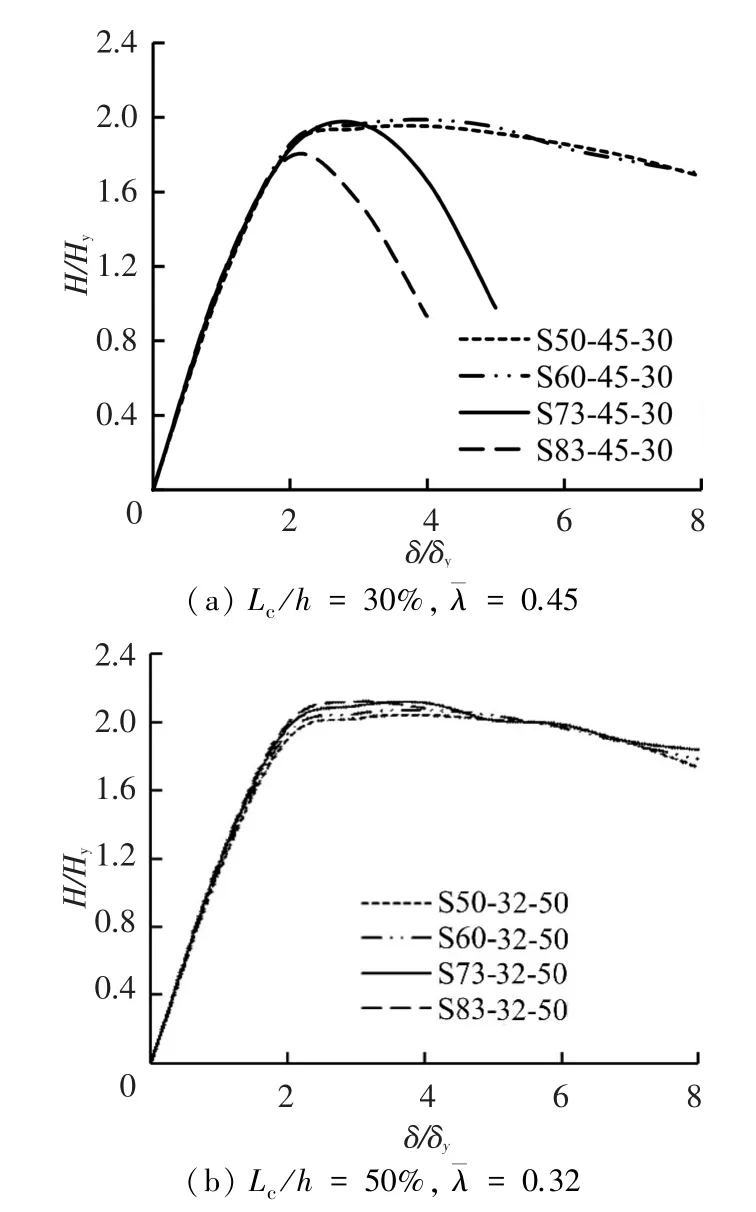
图7 翼缘宽厚比的影响

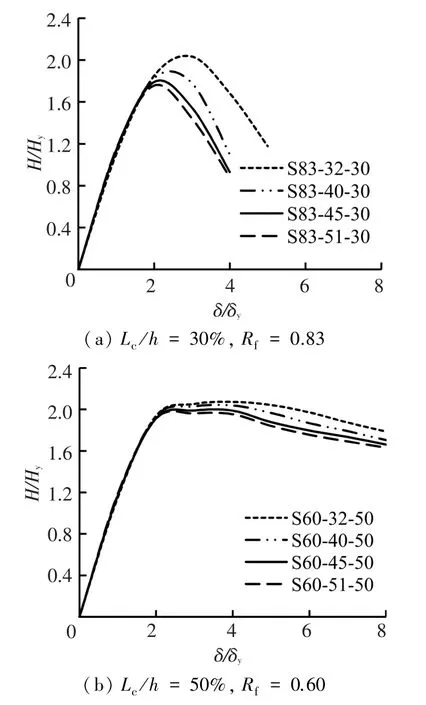
图8 柱长细比的影响

2.2.3 混凝土填充率影响

图9是翼缘宽厚比分别为0.50和0.83时的混凝土填充率影响比较.由于试件S50-32-30和试件S50-32-50（图9（a））的钢板破坏都出现在试件底部附近，它们的极限承载力和延性性能相差不大，且都具有良好的延性性能.该图同时表明混凝土填充率不是越大越好，达到一定的混凝土填充率以后，再继续填充混凝土对提高桥墩延性将作用甚微.图9（b）中纯钢桥墩S83-32-00的极限承载力和延性最小.当混凝土填充率为30%时（S83-32-30），桥墩的极限承载力和延性性能得到显著提高.当混凝土填充率提高到50%时（S83-32-50），虽然桥墩的极限承载力提高不多，但延性性能大为改善.由此可以看出，在钢桥墩内部填充混凝土，可以有效提升桥墩的极限承载力和延性性能.

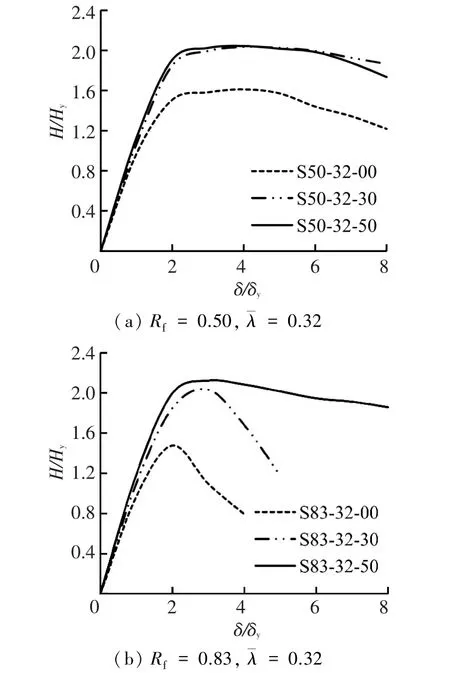
图9 混凝土填充率的影响

2.2.4 柱顶轴压比影响

图10是翼缘宽厚比分别为0.60和0.83时的柱顶轴压比影响比较.该图分别以不考虑轴力影响的柱顶水平屈服荷载Hy0和水平屈服位移δy0对荷载-位移骨架曲线进行无量纲处理．随着柱顶轴压比的增大，内填混凝土钢桥墩的极限承载力（H／Hy0）基本保持不变，但达到极限承载力后的承载力退化速率加快，延性性能变差，这与纯钢桥墩中的轴压比影响有所不同．笔者在文献［13］中指出，纯钢桥墩的极限承载力和延性性能均随轴压比的增大而显著降低．上述差异主要是由于它们之间不同的传力机理造成的．纯钢桥墩中的轴力都由钢板承担，因此轴力变化对纯钢桥墩的极限承载力影响显著，而内填混凝土钢桥墩中的轴力有很大一部分通过横隔板传给混凝土承担，此时的轴力变化（位于0.1Py至0.3Py之间）对内填混凝土钢桥墩的极限承载力影响较小．

图10 柱顶轴压比的影响

3 结 论

1）有限元分析结果和试验结果在荷载-位移滞回曲线和破坏模态的对比上吻合较好，表明采用的有限元分析方法是可行的.

2）对于纯钢桥墩，破坏模态为试件底部附近钢板发生局部屈曲.对于内填部分混凝土钢桥墩，当混凝土填充高度小于最佳填充高度时，破坏模态为内填混凝土上方钢板发生局部屈曲.当混凝土填充高度大于最佳填充高度时，破坏模态均为底部钢板发生向外鼓曲变形，该类桥墩的延性性能最为优越.

3）对于混凝土填充率为30%的钢桥墩，翼缘宽厚比的增大，将导致钢桥墩的极限承载力和延性性能降低；对于混凝土填充率为50%的钢桥墩，翼缘宽厚比的变化对钢桥墩的极限承载力和延性性能影响很小.无论混凝土填充高度如何，柱长细比的增大都导致钢桥墩极限承载力和延性性能的降低.

4）在钢桥墩内部填充混凝土，可以有效提升钢桥墩的极限承载力和延性性能，但达到一定的混凝土填充率以后，再继续填充混凝土对提高桥墩延性将作用甚微.柱顶轴压比越大，内填混凝土钢桥墩的延性性能越差.

［1］韩林海，杨有福.现代钢管混凝土结构技术［M］.北京：中国建筑工业出版社，2004：5-57，152-157.

［2］陈宝春.钢管混凝土拱桥设计与施工［M］.北京：人民交通出版社，2007：1-19，46-91.

［3］MATSUI C.Structural performance and design of concrete filled steel tubular structures［J］.JSSC Steel Construction Engineering，1994，1（2）：11-24.

［4］GE Hanbin，USAMI T.Analytical study on ultimate strength and deformation of partially concrete-filled steel beam-columns of box section［J］.Structural Engineering and Earthquake Engineering，JSCE，1995，513（31）：77-88.

［5］KASAIA，GE Hanbin，USAMIT.Seismic performance of partially concrete-filled steel piers［J］.Bridge and Foundation，1997，31（9）：23-29.

［6］王跃东，高圣彬.内填部分混凝土箱形截面钢桥墩的滞回性能研究［J］.四川建筑科学研究院，2012，38（1）：14-18.

［7］GOTO Y，MIZUNO K.Nonlinear finite element analysis for cyclic behavior of thin-walled stiffened rectangular steel columns with in-filled concrete［J］.Journal of Structural Engineering，ASCE，2012，138：571-584.

［8］GOTO Y，KUMAR G P.Nonlinear finite element analysis for hysteretic behavior of thin-walled circular steel columns with in-filled concrete［J］.Journal of Structural Engineering，ASCE，2010，136：1413-1422.［9］DIANA Material Library［M］.The Netherlands：TNO DIANA BV，Ver.9.4.3，2012.

［10］VECCHIO F J，COLLINS M P.The modified compression field theory for reinforced concrete elements subjected to shear［J］.ACI Journal，1986，83（22）：219-231.

［11］GAO Shengbin，GE Hanbin.Numerical simulation of hollow and concrete-filled steel columns［J］.An International Journal of Advanced Steel Construction，2007，3（3）：668-678.

［12］LIANG Q Q.High strength circular concrete-filled steel tubular slender beam-columns［J］.Journal of Constructional Steel Research，2011，67（2）：164-171.

［13］GAO Shengbin，USAMI T，GE Hanbin.Ductility evaluation of steel bridge piers with pipe sections［J］. Journal of Engineering Mechanics，ASCE，1998，124：260-267.

（编辑 赵丽莹）

Parametric study on ductility behavior of partially concrete-filled steel box-section bridge piers

GAO Shengbin1，XU Minyang2，ZHANG Daxu1
（1.Dept.of Civil Engineering，School of Naval Architecture，Ocean and Civil Engineering，Shanghai JiaoTong University，200240 Shanghai，China；2.Technical Center，Shanghai Xian Dai Architectural Design Co.，Ltd，200041 Shanghai，China）

To investigate the ductility behavior of partially concrete-filled steel box-section bridge piers subjected to a constant vertical load as well as cyclic lateral loads，a three-dimensional elastic-plastic finite element formulation is proposed for numerical simulation.By comparing the lateral load-lateral displacement hysteretic curves and failuremodes of numerical resultswith experimental results，the proposed finite element analysismethod is verified to be accurate and effective.56 analyticalmodels are established with four variable parameters，i.e.，flange plate width-thickness ratio，column′s slenderness ratio，filled-in concrete ratio and axial load ratio.A summary of possible failuremodes is given as follows.For pure steel piers，local buckling occurs near the bottom of the specimen.For partially concrete-filled steel piers，local buckling usually occurs at the upper plate adjacent to filled-in concrete in the case of small filled-in concrete ratio.With the increase of filled-in concrete ratio，local buckling will appear near the bottom of the specimen.Finally，the ultimate strength and ductility behavior of partially concrete-filled steel bridge piers are investigated on the basis of four variable parametersmentioned above.

partially concrete-filled steel bridge pier；numerical simulation；failuremode；ductility behavior

U443.22

A

0367-6234（2014）12-0089-07

2014-05-16.

上海市科学技术委员会浦江人才计划（08PJ1406400）.

高圣彬（1970—），男，副教授，硕士生导师.

高圣彬，gao-sb＠sjtu.edu.cn.