城市客运交通运营者经济决策双层规划模型
胡晓伟,王 健,王 雷(.哈尔滨工业大学交通科学与工程学院,50090哈尔滨;2.哈尔滨工业大学管理学院,5000哈尔滨)
城市客运交通运营者经济决策双层规划模型
胡晓伟1,2,王 健1,王 雷1
(1.哈尔滨工业大学交通科学与工程学院,150090哈尔滨;2.哈尔滨工业大学管理学院,150001哈尔滨)
为分析客运经济政策在不同运营者间的作用规律,应用博弈论分析了城市客运交通运营者之间的Nash均衡,构建了双层规划模型来描述运营者之间的经济决策行为,分析了不同策略下运营者的效益和社会总成本,包括时间、能源消耗和空气污染等成本,其中上层模型分析管理者优化不同客运方式的费率,下层模型分析运营者在限定费率下确定各自的服务频率以获得最大利润.采用GAMS和遗传算法分别构建了双层规划模型的求解算法,算例分析验证了模型的有效性.引入轨道交通服务,可以提高城市公共交通客运份额,有效降低环境、能源等外部性成本.
交通运输经济;城市客运交通;博弈论;双层规划模型;经济决策模型
城市客运交通系统中包含了运营公交、出租车、轨道交通等不同运输工具,而不同客运方式之间既有合作亦有竞争关系,与私家车一起构成了城市客运交通市场的主要部分.城市客运交通系统的某一均衡状态是所有运营者在考虑了其他运营者的策略后的决策结果所构成的稳定状态.
博弈论(game theory)通过严谨的数学模型来研究对抗条件下的最优决策问题,是研究决策主体行为直接相互作用时的决策及其均衡的数学理论和方法.文献[1]将博弈论引入交通领域,在城市客运交通市场分析中得到了广泛的应用.文献[2]基于博弈理论分析了城市客运系统一体化运行战略.文献[3]采用战略博弈思想分析了城市公交市场中的竞争关系.文献[4]建立了公交竞争中n个参与者的非合作博弈模型,并采用启发式算法和灵敏度分析进行求解.文献[5]则基于博弈论研究了城市公交系统中管理者和运营者的非合作Stackelberg关系.文献[6]综述了博弈理论在交通运输领域的应用.而对城市客运交通经济决策的研究,研究人员多使用双层规划模型.文献[7-8]利用双层规划和基于灵敏度分析的算法对道路收费问题进行了研究.文献[9]采用双层规划研究了动态次优收费定价问题,并将其转化为一个非线性规划问题,采用松弛方法进行求解.文献[10]构建了多用户双层规划模型来分析拥挤收费下机场时刻管理问题,目的是降低不同时段航班量的波动和平均延误时间.这些文献从不同的角度剖析了城市客运交通市场中存在的博弈行为,但是既有研究不能有效地分析经济政策下不同客运交通运营者的经济决策,难以保证管理者所制定的客运交通经济政策顺利执行并达到所预期的效果.因此本文运用博弈理论研究经济政策在运营者间合作竞争行为的作用过程,构建双层规划模型来分析经济政策运营者的经济决策行为.
1 城市客运交通运营者Nash均衡分析
1.1 运营者博弈要素分析
设每个运营者i有一个合作竞争策略集合Si,对于∀i∈{1,2,…,n},每个运营者i同时选择一个策略si∈Si,并且其支付函数为ui∈S1× S2×…×Sn→R.
每个运营者的支付函数ui包括了n个策略,可表示为
式中:Ri(Si)为第i个运营者在策略Si下的乘客数量;fi为第i个运营者服务费用(票价);Ci(Ri)为第i个运营者在乘客数量Ri下的广义成本,假设Ci(Ri)=ciFi[Ri(Si)],ci为运营者i的基准广义运营成本;Fi为基于乘客数量的服务频次,Fi=H为运营者i的单位载客量,取整数.
Nash均衡可定义为一系列的策略{SN1,SN2,…,SNn},且ui(SN1,SN2,…,SNn)≥ui(S1,S2,…,Sn),则

1.2 两人博弈的Nash均衡分析
城市客运交通运营者两人博弈的情况,例如城市客运交通市场中除了私家车外,仅有常规公交和出租车两种方式为乘客提供服务,则两者之间的Nash均衡为
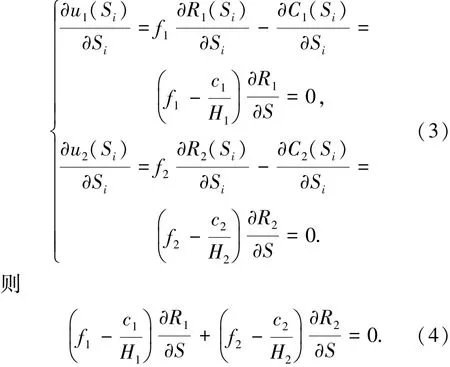
如果忽略广义成本的影响,假设f1=f2=f,则式(4)可转化为

1.3 多人博弈的Nash均衡分析
多人博弈的情况与大多数城市客运交通市场相一致,如除了私家车外,包含常规公交、轨道交通和出租车服务的客运市场.这种情形与两人博弈相类似,但是需要引入一个新的决策量:机会成本.个体运营者将最大化其期望收益,例如最大化期望乘客数量.根据式(4)、(5)的含义,说明运营者需要降低值,即在保证载客量一定的情况下降低每次运行成本,或者在保证运行成本不变的情况下,增加载客量.
一种新的交通方式的引入,会为城市客运交通市场提供新的客运服务和潜在的利润.文献[11]的研究发现需求响应交通(demand responsive transportation,DRT)服务的引入,为城市客运交通市场提供了潜在的利润业务.
2 城市客运交通运营者经济决策建模
研究问题描述:城市客运交通市场中存在着公交、轨道交通、出租车3种公共交通方式,私家车是一种个体交通方式.为简化,每类公共交通方式对应于一个独立的运营者,运营者之间通过竞争将会达到Nash均衡,即3个运营者在竞争中均不能作为领导者.
2.1 城市客运交通运营者市场份额分析
乘客基于自身的个体经济特性和车辆拥有等情况来选择不同的客运交通方式来实现自己效用的最大化,此处采用logit模型来分析乘客的方式选择行为,考虑了乘客的行程时间、等待时间和票价费用.则乘客的效用可表示为

式中:Ui为乘客选择客运方式i的效用,i=1、2、3、4分别对应于公交车、轨道交通、出租车和私家车;tT,i、tW,i分别为乘客选择客运方式i的行程时间和等待时间;fi为乘客选择客运方式i的费用,元/次,其中f4为私家车出行时所支付的停车费用、油费和通行费;a1、a2、a3分别为行程时间、等待时间和票价费用参数.
令Pri为客运方式i的市场份额,根据文献[12]的分析,城市客运交通运营者市场份额可表示为

2.2 模型假设
假设:1)3类公共交通客运方式对应于3个独立的运营者,运营者之间通过竞争将会达到Nash均衡,即3个运营者在竞争中均不能作为领导者.2)乘客将有4种客运方式可供选择,即公交、轨道交通、出租车和私家车.3)双层规划模型中,上层模型是优化管理者制定费率,下层模型是运营者在限定费率下确定服务频率;在管理者(作为领导者)与运营者(作为追随者)之间存在着Stackelberg均衡;同时在运营者(作为领导者)与乘客(作为追随者)之间也存在着Stackelberg均衡.4)采用logit模型分析乘客的方式选择概率. 5)出租车乘客平均等待时间为6 min.
通过对深圳市3 198辆出租车连续运营204 h(2011年4月18日0时至4月26日12时)的GPS数据分析统计得到的平均值.
2.3 城市客运交通运营者经济决策的双层规划模型
上层模型为社会成本的计算,即


其中:CS为社会成本;CT为出行时间成本;PA为空气污染成本;CE为能源消耗成本;bij为社会成本指数,j=1为出行时间指数,j=2为空气污染指数,j=3为能源消耗指数,i=1、2、3、4分别表示公交车、轨道交通、出租车和私家车;Fi为公交、轨道交通和出租车的服务频次;R为乘客总数,人次;Hi为方式i的座位数;d为出行起点与终点之间的距离,km.
下层模型为运营者i的利润,即

其中:ci为每频次(公交、轨道交通和出租车)的平均运营成本,元/次;式(13)为运营者i提供的座位要大于等于该方式的乘客需求;式(14)为服务频次非负和整数约束;式(15)为票价非负和整数约束;式(16)为发车频次与乘客等待时间的关系.
2.4 模型求解
对双层规划模型的求解,研究人员已提出了一些方法[13-14],包括分支定界法、互补旋转法、下降法、惩罚函数法和信任域法.同时,遗传算法[15-16]和GAMS软件[17]也被应用于双层规划模型的求解.
2.4.1 GAMS求解
一般性代数仿真系统(the general algebraic modeling system,GAMS)[18]融合了关系数据库技术和数学规划理论,可求解线性规划,非线性规划和混合整数规划等问题.
在GAMS模型的整体结构中,所需要输入(inputs)和输出(outputs)的内容主要如下所示:1)sets用来指定数学模型中的下标,例如本文所构建模型中不同的客运交通方式、不同的社会成本等.2)data用来指定数学模型中的常量,如本文中的乘客需求、行程时间、等待时间和票价费用参数等,其具体表示方法有lists、tables和direct assignment 3种形式.3)variables用来表示数学模型中的变量,例如所构建模型中的不同客运交通方式的发车频率、市场占有份额等.4)equations用来表示数学模型中方程和约束条件,包括等式和不等式约束,如上层模型和下层模型的目标函数、各约束条件等.5)model and solve用来说明所建立的GAMS模型定义和所采用的求解方法,例如非线性规划(nonlinear programming,NLP)方法、混合整数非线性规划(mixed integer nonlinear programming,MINLP)方法.6)display表示模型结果的输出,例如在本模型中输出不同客运方式的市场份额、上层和下层目标函数值等.
在前文所构建的城市客运交通运营者双层规划模型中,上层模型是管理者确定每种交通方式的优化票价;而在上层模型确定票价之后,下层模型是运营者确定每种交通方式的服务频次;之后运营者的服务频次将会返回到上层模型中,影响管理者最小化社会成本的目标.通过迭代的方法将双层规划模型中上层模型目标函数与下层目标函数相互联系起来.
2.4.2 遗传算法(GA)求解
双层规划模型求解中,可以利用下层规划模型的K-K-T最优性条件代替下层问题,并代入上层规划模型.由于遗传算法对目标函数没有凸性、可微和连续的要求,因此采用这种启发式算法对求解双层规划模型具有适用性.
阶段1 初始化.按照城市客运交通运营者经济决策模型中变量约束范围,随机产生一组初始种群.
阶段2 选择.通过对比染色体,并给出一个合适的函数,来识别解的优劣.本文的目标函数被用来作为适应度函数,并且种群的数量假设是定值.采用惩罚函数将下层模型(12)变化为上层模型(8)的目标函数.上层优化模型可以被简化为一个广义的线性约束规划模型.适应度函数定义为

其中:˜ε是由适应度函数用来选择的,M为惩罚因子.
此外,采用轮盘赌法选择染色体作为父本(parents),通过复制来产生子代(offspring),选择的概率为

其中:Pr(˜εk)为染色体k被选作父本的概率,˜εk为染色体k的适应度值.
阶段3 复制(交叉和变异).交叉是通过分配原则进行配对,然后交叉变化随机产生一组新的解的过程.变异是为保证所有可能的有用信息被复制和保留,通过改变一个或多个染色体上的基因产生新的个体,每个基因发生变异的机会是均等的,其概率值变化在0和1之间.
阶段4 终止.本文采用固定迭代次数来作为遗传算法的终止条件.当算法终止时,可行解的最小值即为遗传算法求得的最优解.
3 城市客运交通运营者经济决策算例分析
3.1 基本参数设置
本案例假设出行者起点到终点的距离为10 km,采用公交、轨道交通、出租车和私家车4种交通方式,出行时间成本bi1,空气污染成本bi2,能源消耗成本bi3,运营成本ci,座位数Hi,最大服务频次Fi,出行时间tT,i各参数值具体见表1[19-20].初始出行需求R为每小时4 000位乘客,结合文献[15],将行程时间参数、等待时间参数和票价费用参数分别取值为a1=-0.003,a2=-0.004,a3=-0.02.

表1 初始参数设置
3.2 模型求解结果及分析
采用MATLAB中的遗传算法工具箱编程求解,结果分别见图1、2,其中公交、轨道交通和出租车对应的票价分别为2、5、16元.
将参数代入GAMS中可以得到模型的求解结果,具体见表2.可以发现在乘客需求为每小时4 000人次的情况下,整体社会成本远高于运营者的收益.公交、轨道交通、出租车和私家车的市场份额比例分别为29.4%、27.7%、22.3%和20.6%,对应的票价分别为2、5、16、20元.此情景下社会成本为80 699元/h,运营者收益为5 164元/h.

图1 基于遗传算法的不同客运方式票价

图2 基于遗传算法的不同客运方式服务频次
对比图1、2和表2可知,采用遗传算法求得的结果与采用GAMS求解的结果一致,验证了GAMS所求得结果的准确性.GAMS由于融合了关系数据库技术和数学规划理论,可以用在双层规划模型的求解中.

表2 引入轨道交通后GAMS模型优化结果
目前我国有12个城市已开通了轨道交通,另有14个城市正在建设轨道交通,这也意味着部分城市目前只有公交和出租车两种公共客运交通方式,分析引入轨道交通的影响,首先要计算城市客运交通市场中仅有公交和出租车两种公共交通方式下的情况(乘客需求和票价不变),结果见表3,在这种情景下社会成本为102 413元/h,运营者收益为4 478元/h.
对比这两种情形可见,引入轨道交通可以有效降低社会成本,包括环境污染和能源消耗成本,降低的比例为21.2%,而运营者的收益得到了提高,提高的比例为15.3%.与此同时,城市客运交通系统中的市场份额发生了变化,私家车的份额从28.5%下降到20.6%,而公共交通整体从71.5%增加到79.4%,反映了引入轨道交通的效果.

表3 无轨道交通时GAMS模型优化结果
由表2、3对比可见,引入轨道交通这种公共交通方式之后,总的社会成本会显著下降,而运营者收益之和也会增加,但是对公交和出租车运营者而言,其利润下降,而新加入的轨道交通运营者收益则是呈增加趋势.为实现城市客运交通市场的和谐、可持续和环保发展,应鼓励发展城市轨道交通,以降低社会成本;同时对公交运营企业和出租车运营企业可通过补贴的方式弥补其损失.
同时,管理者需要考虑引入轨道交通的机会成本和沉没成本[2-3],这是因为轨道交通的巨额投资和较长的施工建设期所引起的.在管理机构制定了公共交通票价(私家车停车费、通行费)之后,运营者可以作出各自的运营服务频次决策.而管理机构对公共交通的补贴可以吸引乘客选择公共交通方式,促进城市客运交通方式结构的变化.
4 结 论
1)基于博弈理论剖析了城市客运交通运营者间的均衡关系,构建了双层规划模型分析运营者的经济决策行为,揭示了客运经济政策在不同运营者间的作用规律.
2)双层规划模型中,上层模型的目标函数是管理者优化不同客运方式的费率实现社会总成本最小化,包括了出行时间成本、空气污染成本和能源消耗成本;下层模型是运营者在限定费率下优化各自的服务频率实现收益最大化.
3)采用GAMS和遗传算法分别设计了双层规划模型的求解算法,模拟了客运交通市场中是否引入轨道交通下运营者的经济决策行为.未来将考虑政府补贴、出行者不同的出行时间价值等情况,拓展和完善模型,以期最大程度贴合实际中的多变状况,为运营者的决策实践提供帮助和参考.
参考文献
[1]FISK C S.Game theory and transportation systems modeling[J].Transportation Research Part B,1984(4/5):301-313.
[2]ROUMBOUTSOS A,KAPROS S.A game theory approach to urban public transport integration policy[J].Transport Policy,2008,15:209-215.
[3]WANG J Y T,YANG H.A game-theoretic analysis of competition in a deregulated bus market[J]. Transportation Research Part E,2005,41:329-355.
[4]ZHOU J,LAM W H K,HEYDECKER B G.The generalized nash equilibrium model for oligopolistic transitmarketwith elastic demand[J].Transportation Research Part B,2005,39:519-544.
[5]SUN L J,GAO Z Y.An equilibrium model for urban transitassignment based on game theory[J].European Journal of Operational Research,2007,181:305-314.[6]HOLLANDER Y,PRASHKER JN.The applicability of non-cooperative game theory in transport analysis[J]. Transportation,2006,33:481-496.
[7]YANG H,LAM W H K.Optimal road tolls under conditions of queuing and congestion[J]. Transportation Research A,1996,30:319-332.
[8]YANG H,MICHAEL G H B.Traffic restraint,road pricing and network equilibrium[J].Transportation Research B,1997,31:303-314.
[9]BAN X,LIU H X.A link-node discrete-time dynamic second best toll pricingmodelwith a relaxation solution algorithm[J].Networks and Spatial Economics,2009,9(2):243-267.
[10]王琨,朱金福,高强.采用拥挤收费的机场时刻管理多用户双层规划模型[J].哈尔滨工业大学学报,2014,46(5):120-124.
[11]BRAKE J,NELSON J D.A case study of flexible solutions to transport demand in a deregulated environment[J].Journal of Transport Geography,2007,15:262-273.
[12]BEN-AKIVA M,LERMAN S.Discrete choice analysis:theory and application to travel demand[M]. Cambridge:MIT,1985.
[13]MIGDALASA.Bilevel programming in traffic planning:Models,methods and challenge[J].Journal of Global Optimization,1995,7:381-405.
[14]COLSON B,MARCOTTE P,SAVARD G.An overview of bilevel optimization[J].Annuals of Operations Research,2007,153:235-256.
[15]王健.道路拥挤定价下的公共交通收费问题研究[D].哈尔滨:哈尔滨工业大学,2003:80-102.
[16]CHIOU Y C,LAN L W,CHANG K L.Sustainable consumption,production and infrastructure construction for operating and planning intercity passenger transport systems[J].Journal of Cleaner Production,2013,40:13-21.
[17]ZITO P,SALVO K,FRANCA L L.Modelling airlines competition on fares and frequencies of service by bilevel optimization[J].Procedia Social and Behavioral Sciences,2011,20:1080-1089.
[18]ROSENTHAL R E.GAMS—a user’s guide[R]. Washington DC:2010 GAMSDevelopment Corporation,2010.
[19]Transportation Research Board.Transit capacity and quality of service manual[R]//Transit Cooperative Research Program(TCRP)Report 100.2nd ed. Washington DC:Transportation Research Board,2003.
[20]ZHANG S,ZHOU W,SHAO C.Evaluation of urban passenger transport structure[J].Proceedings of the Eastern Asia Society for Transportation Studies,2005,5:441-449.
(编辑 魏希柱)
Econom ic decision-making bi-level programm ing model for urban passenger transportation operators
HU Xiaowei1,2,WANG Jian1,WANG Lei1
(1.School of Transportation Science and Engineering,Harbin Institute of Technology,150090 Harbin,China;2.School of Management,Harbin Institute of Technology,150001 Harbin,China)
To analyze the law of passenger transportation economic policy in different operators,based on game theory to describe the Nash equilibrium among urban passenger transportation operators,a bi-level programmingmodel is proposed tomodel urban passenger transportation operators’economic decision-making,operators’profit and social cost have been discussed,including the travel time cost,air pollution cost and energy consumption cost.The upper-levelmodel describes themanagementauthority’regulation on the fares of each mode,the lower-level model describes the operators’maximum profit by determining the service frequency.Based on GAMS and genetic algorithm,a numerical example verifies the validity of the proposed model.The introduction of subway service will increase the total market share of passenger public transportation,and effectively reduce the external cost,including the environmental emission cost and energy consumption cost.
transportation economy;urban passenger transportation;game theory;bi-level programming model;economic decision-makingmodel
U491
A
0367-6234(2014)12-0059-06
2013-05-02.
国家自然科学基金(71073035);中国博士后科学基金(2013M540299);中央高校基本科研业务费专项资金(HIT.NSRIF.2015075).
胡晓伟(1984—),男,讲师,博士;王 健(1974—),男,教授,博士生导师.
胡晓伟,hxwhit@163.com.

