基于迭代平方根CKF的SLAM算法

高 伟，张 亚，孙 骞，关 劲（.哈尔滨工程大学自动化学院，5000哈尔滨；.海军装备部，00036北京）

基于迭代平方根CKF的SLAM算法

高 伟1，张 亚1，孙 骞1，关 劲2
（1.哈尔滨工程大学自动化学院，150001哈尔滨；2.海军装备部，100036北京）

在大尺度环境中，平方根容积卡尔曼同步定位与地图构建算法的非线性误差严重制约了算法的定位精度，为解决这一问题，提出了一种基于迭代平方根容积卡尔曼滤波的改进算法，该算法结合迭代理论，对平方根容积卡尔曼滤波的量测更新过程进行迭代更新，充分利用最新的观测信息，降低滤波的估计误差，从而构建精确的地图并获得高精度的定位信息.仿真实验结果表明，采用本算法后，x轴和y轴方向上的位置误差均在1.5m以内，估计结果明显优于SRCKFSLAM、CKF-SLAM和EKF-SLAM算法；添加不同的环境噪声后进行仿真实验，该算法所取得的位置误差相比仍是最小的.利用该算法可以有效地减小非线性误差造成的影响，提高SLAM的定位精度.

迭代理论；同步定位与地图构建；非线性误差；平方根容积卡尔曼滤波；迭代平方根容积卡尔曼滤波

同步定位与地图构建（simultaneous localization and mapping，SLAM）是指运载体在完全未知的环境中，依靠自身携带的传感器对周围环境进行观测和识别，并利用获得的观测信息自主创建环境地图，同时利用该地图对运载体进行定位与导航［1-4］.目前SLAM问题的解决方法主要以概率估计为主，其中应用最为广泛的方法是基于扩展卡尔曼滤波（extended Kalman filter，EKF）的SLAM算法［5-7］.但是该算法在线性化过程中会引入较大的截断误差，并且计算量较大，不适用于复杂环境.针对上述不足，Julier等提出了基于无迹卡尔曼滤波（unscented Kalman filter，UKF）的SLAM算法，但当系统为高维时，UKF滤波过程中的协方差容易出现非正定情况，从而导致滤波数值不稳定且有可能发散［8-9］.为克服UKF-SLAM算法中存在的问题，很多学者开始研究基于容积卡尔曼滤波（cubature Kalman filter，CKF）和基于平方根CKF（square root cubature Kalman filter，SRCKF）的SLAM算法［1，10-11］.由于CKF是通过对一组具有相同权重的cubature点经过非线性系统方程转换来预测下一时刻系统的状态，从而避免了“维数灾难”.与CKF不同，SRCKF算法在滤波过程中直接以协方差矩阵的平方根形式进行递推更新，这样不仅可以降低计算复杂度，获得更高的计算效率，而且能够保证了协方差矩阵的对称性和非负定性，有效地避免滤波器的发散，提高滤波的收敛速度和数值稳定性［12-13］.但是在大尺度复杂环境中，观测过程中大量路标特征的加入会使得系统初始误差增大，量测方程高度非线性化，从而导致cubature点的非线性近似误差逐渐增大，降低了SRCKF-SLAM算法的估计精度，最终使得状态估计和地图构建误差增大［14-15］.为解决上述不足，本文在SRCKF算法的基础上，结合迭代方法，提出一种基于迭代平方根容积卡尔曼滤波（iterated square root cubature Kalman filter，ISRCKF）的SLAM算法.该算法汲取了SRCKF滤波的优点并充分利用最新观测信息，在大尺度复杂环境中可有效地降低系统状态的估计误差，提高地图构建的准确性及导航精度.

1 同步定位与地图构建

SLAM问题的本质是在整个路径中对系统状态的估计问题，系统状态包括载体的状态和观测到的环境中路标特征的状态［1］.设系统状态量x和协方差矩阵P分别为

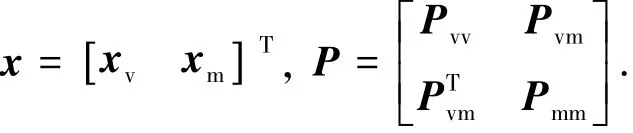
其中：xv为载体的状态量，包括载体在x轴和y轴的位置以及载体的航向角；xm为环境中路标特征的状态量，包括各路标特征在x轴和y轴的位置（xi，yi），其中i=1，2，…，l，l为路标的索引；Pvv为载体的协方差矩阵；Pmm为地图的协方差矩阵；Pvm为载体与地图的关联协方差矩阵．

SLAM问题即可转化为求取系统状态向量的后验概率密度问题，设k时刻系统状态向量和观测量分别为xk和zk，根据贝叶斯公式，状态量的后验概率密度为［2］

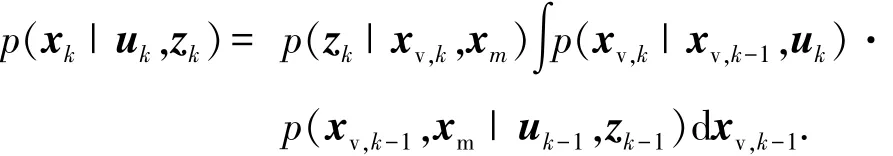
其中：uk为控制输入，p（xv，k｜xv，k-1，uk）为运动模型，p（zk｜xv，k，xm）为量测模型．

2 基于SRCKF的SLAM算法

假设离散非线性系统为

其中：xk为k时刻系统的状态向量，zk为k时刻系统状态的量测值，f（·）和h（·）分别为非线性的状态方程和量测方程，Wk-1～N（0，Q）和Vk～N（0，R）分别为系统噪声和观测噪声．

对于系统（1），SRCKF选取2n（n为系统状态向量的维数）个具有同等权值的容积点计算高斯权重分布，然后通过时间更新和量测更新即可得到SRCKF滤波算法，其中容积点集（ξi，wi）为

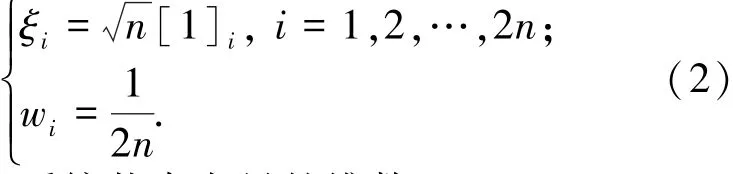
其中：n为系统状态向量的维数.

基于SRCKF的SLAM算法步骤如下［1，14］.

时间更新．假设p（xk-1）=N（x＾k-1｜k-1，Pk-1｜k-1）已知，利用Cholesky分解协方差矩阵Pk-1｜k-1= S ST，计算cubature点X= k-1｜k-1k-1｜k-1i，k-1｜k-1+通过非线性状态方程传播=状态预测=估计预测误差协方差矩阵的平方根为

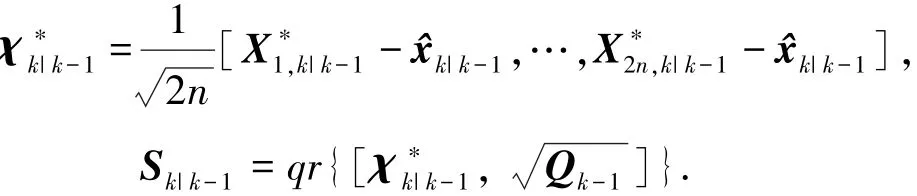
估计滤波增益与状态估计值分别为

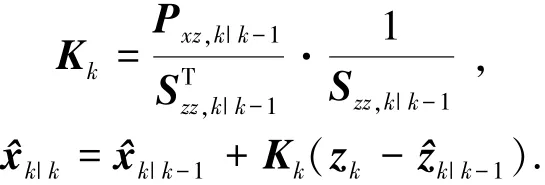
状态误差协方差矩阵平方根为

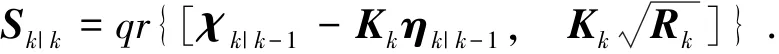
通过上述递推，在给定条件后即可实现对SLAM的观测更新，完成对系统状态的估计，从而确定载体在环境中的位置并实现地图的构建.但是在大尺度复杂环境中，随着观测的进行，大量路标特征的加入会使得系统的初始误差较大，量测方程的非线性度越来越高，cubature点的非线性近似误差也会逐渐增大，从而导致SRCKF-SLAM算法的滤波估计精度降低，甚至发散.

3 基于ISRCKF的SLAM算法

针对SRCKF-SLAM算法中存在的问题，本文利用迭代更新算法，提出了基于ISRCKF的SLAM算法.该算法的核心思想是：利用状态量预测值和协方差平方根的预测值，将量测更新过程利用迭代更新进行多次迭代，充分利用最新的观测信息，从而有效减小估计误差，提高算法的估计精度.

基于ISRCKF的SLAM算法过程描述如下.时间更新.在k时刻，按照第2节基于SRCKF的SLAM算法计算系统状态预测x＾k｜k-1和状态误差协方差矩阵平方根Sk｜k-1．

量测更新．量测更新是以x＾k｜k-1和Sk｜k-1为初始值的迭代过程．记第j次迭代的估计值和方差的平方根分别为x＾（j）和S（j），则量测更新的初始值为

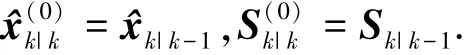
对于j=0，1，2，…，Nmax（其中Nmax为最大迭代次数），计算新的cubature点

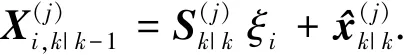
按照下式进行更新，可以得到j次迭代的状态和方差矩阵的平方根矩阵为

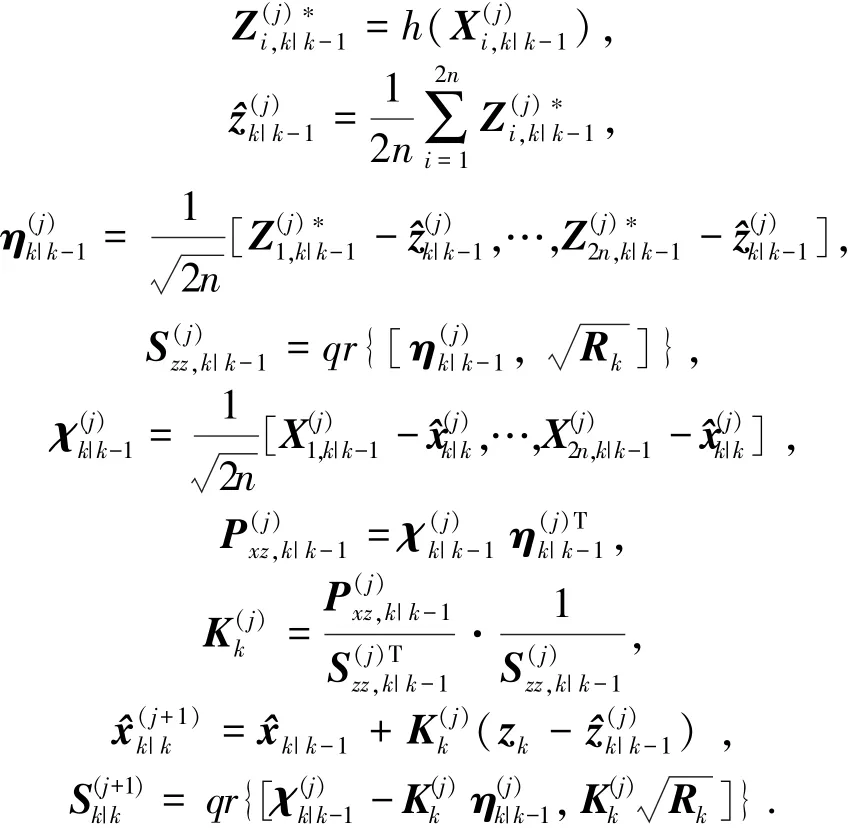
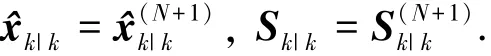
4 算法的实验验证与分析

4.1 实验条件

为了验证本文所提SLAM算法的有效性和可行性，通过MATLAB仿真验证.仿真环境采用悉尼大学学者Tim Bailey发布的开源SLAM仿真器中设置的实验环境.该实验环境在一个250 m× 200 m的室外环境区域中，其中包括人为设置的17个载体运行路径点和135个静止的路标特征，载体从（0，0）处开始逆时针沿路径点确定的轨迹运行，具体的实验环境如图1所示.

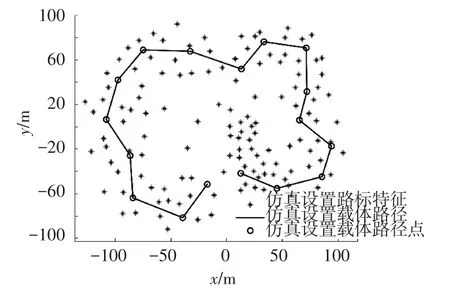
图1 仿真实验环境示意

载体的运动模型为

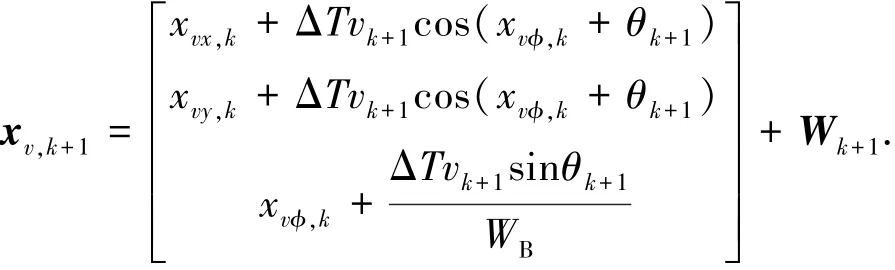
其中：［xvx，k，xvy，k，xvφ，k］T为k时刻载体的位姿，xv，k+1为载体在k+1时刻的位姿，ΔT为采样时间，vk+1和θk+1分别为k+1时刻载体的速度和航向角，WB为两轴间的轴距，Wk+1为k+1时刻的系统误差，且有W～N（0，Q）．

观测模型为

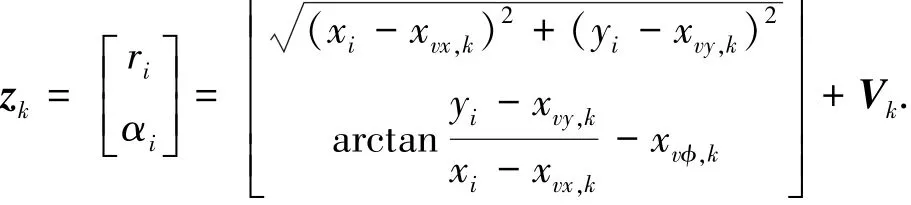
其中：（xi，yi）为探测到的第i个路标特征的位置坐标，ri和αi分别为传感器观测到的第i个路标特征与载体之间的距离及其与载体前进方向的夹角，Vk为k时刻的量测误差，且Vk～N（0，R）．

实验参数设置如下：载体的初始状态xv，0=［0，0，0］T，采样时间ΔT=0.025 s，速度v= 3 m／s，速度误差σv=0.25 m／s，航向角误差σφ=2°，最大角速度20°／s；量测的采样时间为0.2 s，最大观测距离为30 m，距离误差σr= 0.2 m，角度误差σα=1°；最大迭代次数设为20次．系统噪声Q和观测噪声R分别为

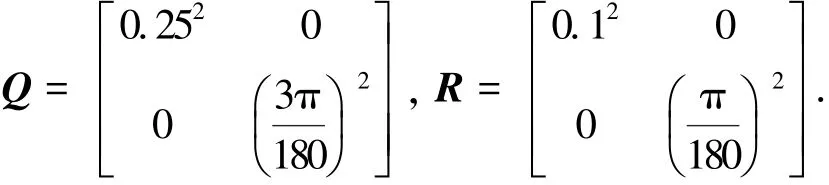
4.2 实验结果与分析

在上述实验环境下，分别对ISRCKF-SLAM、SRCKF-SLAM、CKF-SLAM和EKF-SLAM算法进行了20次独立重复仿真实验，并对实验结果的均方根误差（rootmean square error，RMSE）进行对比分析.

图2为4种SLAM算法对路径的估计结果对比图，图3为SRCKF-SLAM和ISRCKF-SLAM算法对路标的估计结果对比图.其中图2（b）、3（b）分别对应图2（a）、3（a）中矩形区域的局部放大图.

由图2、3可知，在运载体导航定位估计方面，ISRCKF-SLAM算法与SRCKF-SLAM、CKFSLAM和EKF-SLAM算法相比，估计路径和运载体真实路径契合度高，即ISRCKF-SLAM算法估计的精度高于其他3种算法.

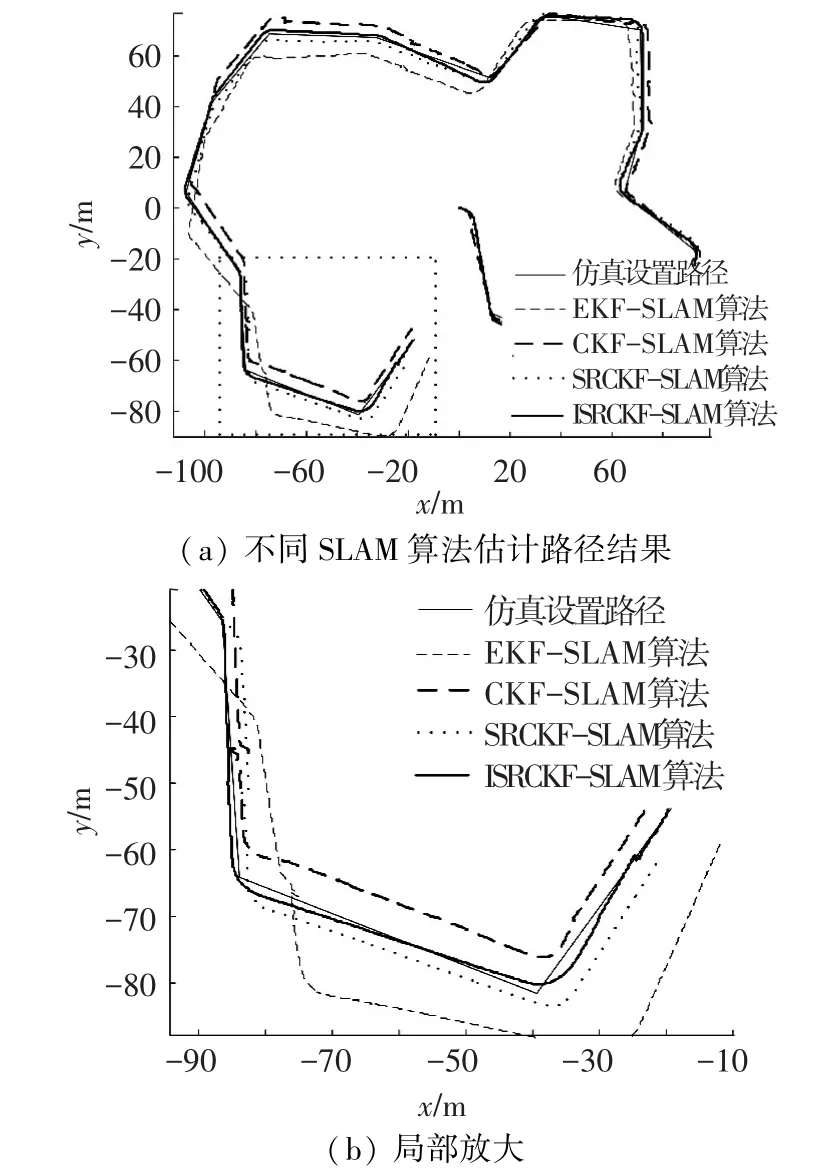
图2 ISRCKF-SLAM和SRCKF-SLAM、CKFSLAM、EKF-SLAM算法估计路径对比

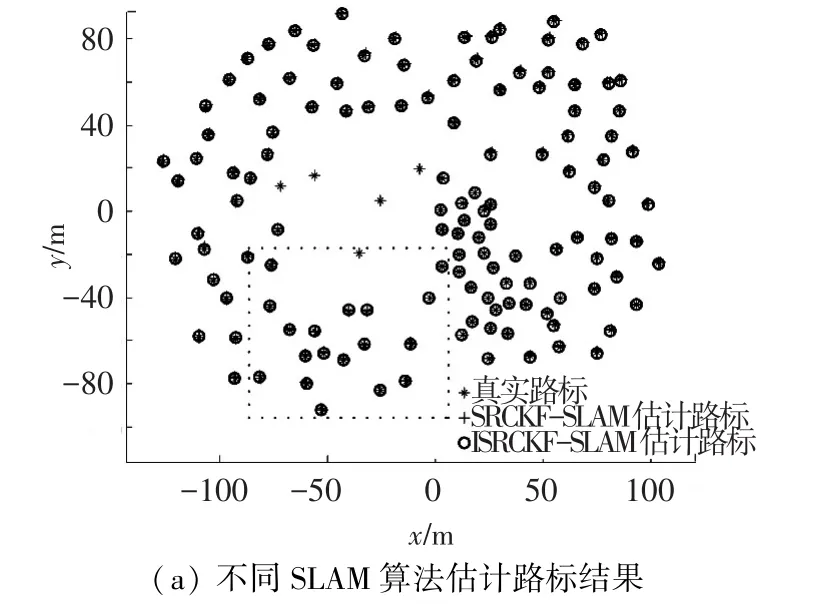
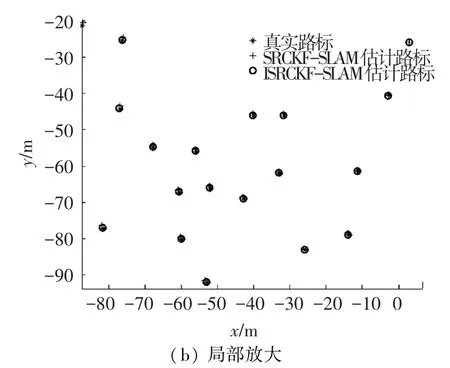
图3 ISRCKF-SLAM和SRCKF-SLAM算法估计路标对比

图4 、5为ISRCKF-SLAM、SRCKF-SLAM、CKF-SLAM和EKF-SLAM算法对载体运行路径x轴、y轴方向上的位置估计误差对比曲线．

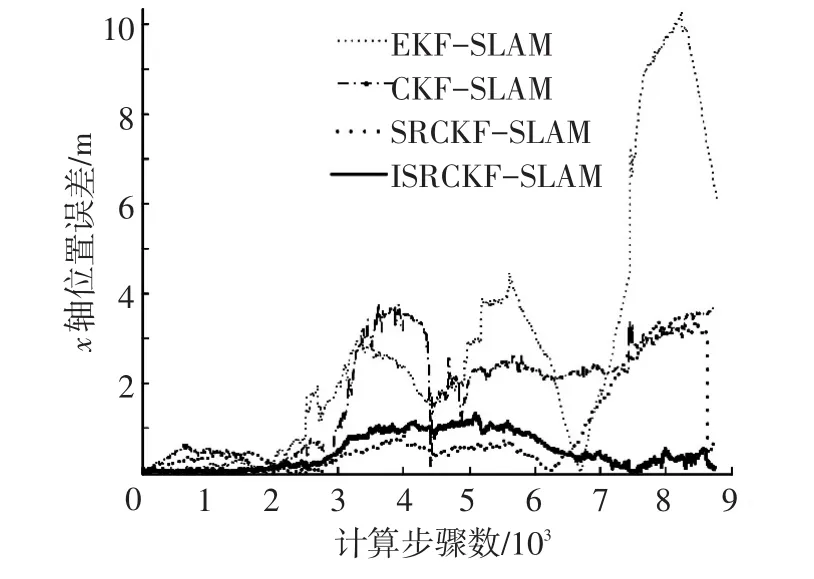
图4 4种SLAM算法下x轴方向位置估计误差对比

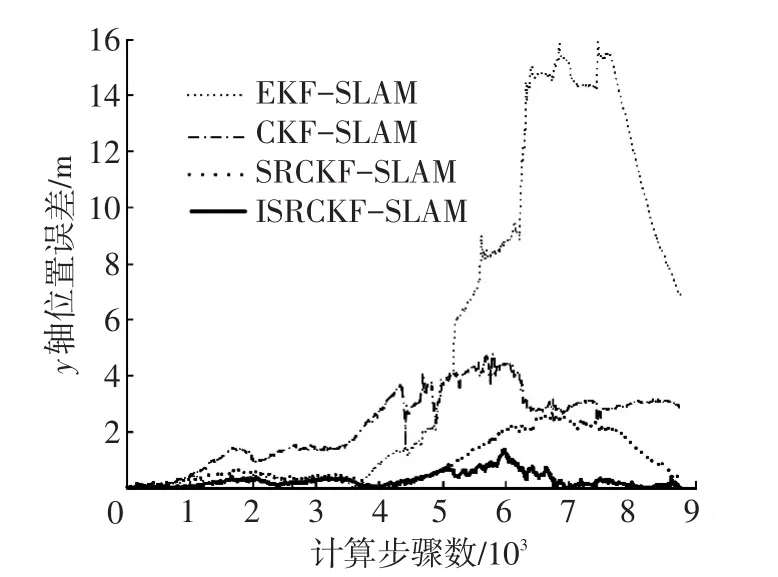
图5 4种SLAM算法下y轴方向位置估计误差对比

由图4、5的实验结果可知利用ISRCKFSLAM算法所得到的x轴和y轴方向位置估计误差均小于1.5 m；SRCKF-SLAM算法和CKFSLAM算法精度略低于ISRCKF-SLAM算法，位置估计误差均在4m以内；KF-SLAM算法的估计精度最差，位置估计精度在16m以内.因此SRCKFSLAM算法的估计精度优于其他3种算法，理论分析一致.由图4可以看出，虽然SRCKF-SLAM算法在前6 000步之前的估计精度均高于ISRCKF-SLAM，但后半部分误差迅速增大.这是由于随着观测的进行，大量路标特征的加入使得系统状态初始误差增大，并且系统高度非线性化，从而引起cubature点的非线性近似误差逐渐增大，系统的非线性误差越来越大，进而导致SRCKF-SLAM算法误差增大.而本文所提出的ISRCKF-SLAM算法通过迭代充分利用了最新的观测信息，有效降低了估计误差，提高了算法的估计精度.综上所述，在运载体运动的全过程中，ISRCKF-SLAM算法的定位估计精度高、误差小，且数值稳定性好，从而验证了ISRCKF-SLAM算法的有效性和优越性.

为了充分验证ISRCKF-SLAM算法的稳定性，添加不同的环境噪声重新进行仿真，其他参数不变.设观测噪声服从以下混合高斯分布，即

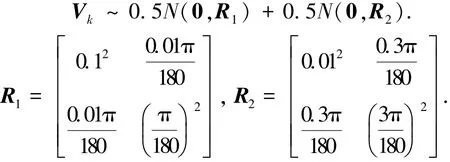
图6为ISRCKF-SLAM算法对载体运行路径x轴、y轴方向上的位置估计误差曲线．

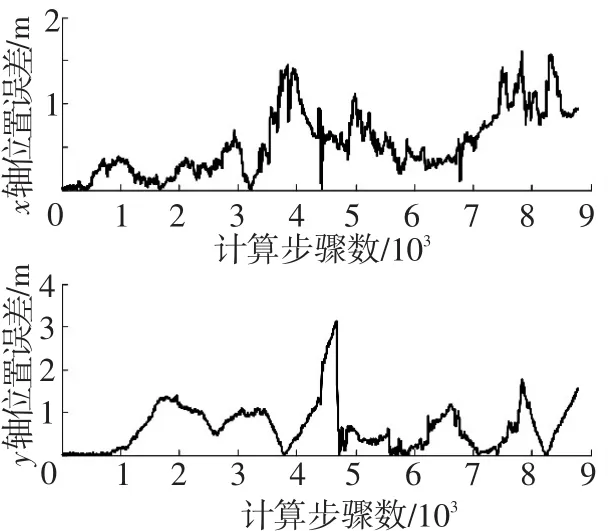
图6 ISRCKF-SLAM算法下运载体位置估计误差

从图6可以看出，在添加不同环境噪声后，ISRCKF-SLAM算法仍然能够较好地估计出运载体的运动轨迹，可取得较高的定位精度.

5 结 论

1）提出了一种基于ISRCKF的SLAM算法，该算法将迭代理论与平方根CKF滤波方法相结合，充分利用最新的观测信息，有效地解决了在复杂环境下量测信息增加导致cubature点的分布逐渐失真的问题，从而保证了滤波的数值稳定性，大大提高了系统状态的估计精度.

2）在相同的仿真环境中，对不同的SLAM算法进行仿真实验对比.仿真结果表明，所提出的ISRCKF-SLAM算法的估计误差小于与其他几种SLAM算法，通过仿真实验验证了本算法的稳定性.

［1］王宏健，傅桂霞，边信黔，等.基于SRCKF的移动机器人同步定位与地图构建［J］.机器人，2013，35（2）：200-207.

［2］袁赣南，王丹丹，魏延辉，等.水下石油管道漏油检测定位的粒子滤波SLAM算法［J］.中国惯性技术学报，2013，21（2）：204-208.

［3］杜航原，郝燕玲，高忠强，等.基于鲁棒非线性卡尔曼滤波的自适应SLAM算法［J］.宇航学报，2012，33（5）：620-627.

［4］张国良，汤文俊，敬斌，等.辅助粒子滤波算法改进的UFastSLAM算法［J］.哈尔滨工业大学学报，2012，44（11）：123-128.

［5］WILLIAMS B，CUMMINS M，NEIRA J，et al.A comparison of loop closing techniques in monocular SLAM［J］.IEEE Transactions on Robotics and Autonomous Systems，2009，57（12）：1188-1197.

［6］王宏健，王晶，边信黔，等.基于组合EKF的自主水下航行器SLAM［J］.机器人，2012，34（1）：56-64.

［7］田翔，张亮，陈耀武.基于中心差分卡尔曼滤波器的快速SLAM算法［J］.哈尔滨工业大学学报，2010，42（9）：1454-1461.

［8］JULIER S，UHLMANN J，DURRANTF.A newmethod for the nonlinear transformation of means and covariances in filters and estimators［J］.IEEE Transactions on Automatic Control，2000，45（3）：477-482.

［9］YAN Xuejun，ZHAO Chunxia，XIAO Jizhong.A novel FastSLAM algorithm based on iterated unscented Kalman filter［C］／／Proceeding of IEEE International Conference on Robotics and Biomimetics.Phuket：IEEE，2011：1906-1911.

［10］PAKKI K，CHANDRA B，GU D，et al.Cubature Kalman filter based localization andmapping［C］／／18th IFAC World Congress.Laxenburg，Australia：IFAC，2011：2121-2125.

［11］ARASARATNAM I，HAYKIN S.Cubature Kalman filters［J］.IEEE Transactions on Automatic Control，2009，54（6）：1254-1269.

［12］GAOWei，ZHANG Ya，WANG Jianguo.A strapdown interial navigation system／Beidou／Doppler velocity log integrated navigation algorithm based on a cubature Kalman filter［J］.Sensors，2014，14（1）：1511-1527.

［13］YU Fei，SUN Qian，LÜChongyang，et al.A SLAM algorithm based on adaptive cubature Kalman filter［J］. Mathematical Problems in Engineering，2014，2014：1-11.

［14］郝燕玲，杨峻巍，陈亮，等.基于SRCKF的水下航行器动基座初始对准技术［J］.华中科技大学学报：自然科学版，2012，40（2）：123-127.

［15］SMIDL V，PEROUTKA Z.Advantages of square-root extended Kalman filter for sensorless control of AC drives［J］.IEEE Transactions on Industrial Electronics，2012，59（11）：4189-4196.

（编辑 魏希柱）

Simultaneous localization and mapping based on iterated square root cubature Kalman filter

GAOWei1，ZHANG Ya1，SUN Qian1，GUAN Jin2
（1.College of Automation，Harbin Engineering University，150001Harbin，China；2.Navy Equipment Department，100036 Beijing，China）

In large-scale conditions，the large nonlinear error of simultaneous localization and mapping（SLAM）based on square root cubature Kalman filter（SRCKF）is a serious constraint to high positional accuracy.To solve this problem，an improved SLAM algorithm based on iterated square root cubature Kalman filter（ISRCKF）is proposed.Utilizing the iteration theory，the newest observation information is in full use. Thus the estimation errors of the new algorithm will be decreased noticeably，an accurate environmentmap will be established and high-precision localization will be obtained as well.The simulation results show that the location errors of x axis and y axis are both less than 1.5 m by the new algorithm.The estimating accuracy of the new algorithm is higher than that of SRCKF-SLAM，CKF-SLAM and EKF-SLAM algorithms.Adding different environmental noises，the position errors of ISRCKF are the smallest.

iterated theory；SLAM；nonlinear error；SRCKF；ISRCKF

U666.1

A

0367-6234（2014）12-0120-05

2013-09-13.

国家自然科学基金（51179039）；武器装备预研基金（9140A09040211CB0102）.

高 伟（1977—），男，教授，博士生导师.

张 亚，yzhang＠hrbeu.edu.cn.