散射体旋转角对二维声子晶体带隙结构影响分析
杜敬涛,贺彦博,冯浩成
(哈尔滨工程大学动力与能源工程学院,黑龙江哈尔滨150001)
散射体旋转角对二维声子晶体带隙结构影响分析
杜敬涛,贺彦博,冯浩成
(哈尔滨工程大学动力与能源工程学院,黑龙江哈尔滨150001)
为探讨散射体旋转作用对于弹性波在声子晶体中的传播特性产生的影响,采用平面波展开法将散射体与晶格轴线夹角因素引入结构函数,研究了在不同填充率下,伴随着旋转角的变化,正方形、椭圆形、正六边形散射体禁带出现的位置及宽度变化情况。研究结果表明:散射体旋转角度对二维声子晶体带隙结构具有显著影响,并且散射体旋转角对正六边形、正方形散射体的影响明显大于对于椭圆形散射体的影响;然而,无论散射体取为何种形状,旋转角度对声子晶体产生禁带的位置(禁带中间频率)影响并不明显。
声子晶体;带隙;禁带;旋转角;平面波展开法;散射体
声子晶体是指具有弹性波带隙的周期性复合材料或结构,作为一种新型声学功能带隙材料,声子晶体的研究不仅具有重要的理论价值,同时具有广阔的应用前景,可以为减振降噪提供一种全新的技术思路[1-2]。为此,声子晶体已经成为国际学术界的研究热点。尽管对于弹性波在层状介质中的传播特性的研究已有近70年的历史,但是声子晶体概念的提出及相关理论的研究时间并不长。1992年,Sigalas等从理论上证实了周期结构中弹性波禁带现象的存在[3],随后,Kushwaha等首次提出声子晶体概念[4]。1995年,Martinez-Sala等从实验角度对弹性波禁带特性进行了观测[5]。从此,声子晶体的研究引起了全世界学者的关注。
就目前研究状况而言,对于散射体在晶格中整齐排列理想情况的研究已经获得了较好的进展。无论是二维或三维的情况,只有在一定条件下才能产生弹性波或声带波间隙。在进行二组元二维声子晶体的研究过程中,散射体排列方式多采用正方形[6]、六边形[7]、氯化钥排列[8]等。散射体截面积大部分采用圆形,少数则采用正方形。但以上研究都存在不足,即一旦晶体制备完成,在实际使用的过程中无法根据实际需要调整带隙位置及宽度。
以上不足得到了中外学者的关注并提出了各自的解决方案。具体如K.Bertodi等提出了施加外应力的方案,从而拓宽了声子晶体带隙[9-11]。此外,颜琳等通过散射体旋转作用,从而成功地探究了声子晶体带隙宽度与旋转角度的关系[12]。与此类似,吴福根也对于液体—液体环境下,正方形散射体偏转角度对于带隙结构产生的影响进行了研究[13]。但是他们的研究成果仅限于正方形散射体,对于其他形状的散射体并未涉及。
基于散射体旋转角对于声子晶体禁带的产生具有一定影响的事实将对于实际过程中人为调整声子禁带的位置及宽度具有极大的指导意义,本文在之前的基础上进行了更为深入的研究,包括正方形散射体六边形散射体以及椭圆形散射体。
1 理论模型
依据弹性动力学理论,在材料的连续性均匀性、完全线弹性、小变形、无初始应力等基本假设下,分别建立描述质点力、位移以及应力应变之间的三类基本方程[14],首先是运动微分方程:

式中:σ是应力,ρ为质量密度,u表示质点的振动位移。
描述应变位移关系的几何方程为
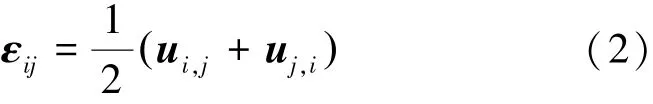
式中:ε表示应变。描述应力—应变关系的物理方程为
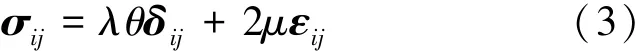
此处采用了张量理论中的爱因斯坦规则。在求解时,先将几何方程(2)代入物理方程(3),在得到用位移表示的应力分量后,将其代入运动方程(1),通过整理后可以得到以位移为未知函数的运动方程:
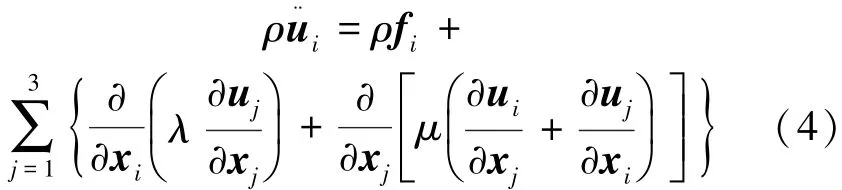
式中:u(r,t)是位移矢量,λ(r)与μ(r)是拉梅常数,ρ(r)是介质的质量密度,它们与纵波波速及横波波速之间的关系为
纵波波速:横波波速:


在研究弹性波在声子晶体内产生的带隙作用时,平面波展开法是常用的方法[14]。其基本思想是:由于声子晶体具有结构周期性,故而可以将弹性常数、密度等参量按照傅里叶级数展开,并与Bloch定理相结合,将弹性波波动方程在倒格矢空间内以平面波叠加的方式展开,即将波动方程转换为本征值求解,从而得到声子晶体的能带结构。由于结构的周期性,拉梅参数λ、μ和密度ρ都是空间r=(x,y)的周期性函数,从而将各材料参数进行傅里叶级数展开:(此处使用函数g统一来表示各材料参量)通过相关推导,可将傅里叶展开系数g(G)表示为

式中,G为倒格矢,对于二维晶格,倒格矢定义为

P(G)为散射体的几何参数,其定义为
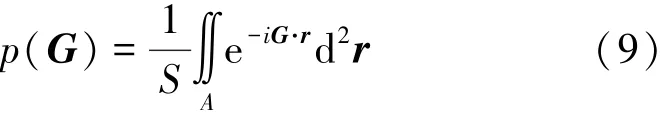
由于散射体形状多种多样,产生的结构函数也互不相同,其显现出的能带特性也有许多差别,本文重点讨论正方形晶格条件下几种具有代表性的散射体能带特性,即:圆形、椭圆形、正方形及正六边形。
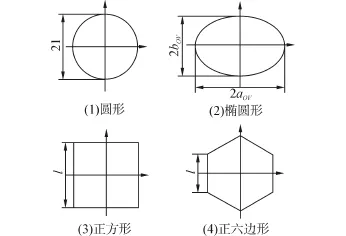
图1 不同形状散射体示意图Fig.1 Different shapes of scatters
对于图1所示的圆形、椭圆形、正方形、正六边形散射体,其形状不同主要体现在结构函数P(G)的差异,采用不同的散射体形状,其结构函数可表示为[15]
1)圆形:

式中:J1(·)为一阶第一类Bessel函数。
2)椭圆形:

式中:Gx'=Gxaov/bov,Gy'=Gy,aov为长半轴的长度,bov为短半轴的长度。
3)正方形:

4)正六边形:

如前所述,在实际中由于加工误差及环境因素的存在,散射体的排列方式可能并不是整齐划一,而是存在一定旋转角,经转化可以得出以下关系式[16]:
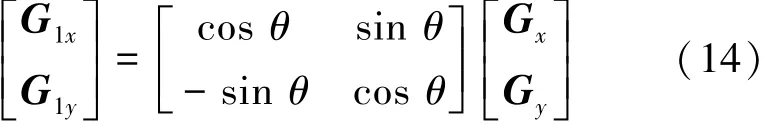
位移场由于结构的周期性,故而可以采用Bloch定理进行分解,产生结果为

式中:k为限制在第一Brillouin区内的Bloch波矢,uk(r)是与各材料参数具有相同周期的函数,同样将其展成傅里叶级数的形式[17-18]:

将以上理论推导的结果采用特征矩阵的形式,可以表示为[17]
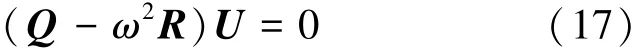
式中:Q和R分别为刚度矩阵和质量矩阵。通过求解这个标准的矩阵特征问题,并绘制特征频率Ω=ωa/2πCt与波数关系曲线,即可得到声子晶体的带隙结构。
2 数值结果与讨论
本节采用MATLAB对上述散射体旋转的二维声子晶体带隙结构进行仿真计算。以铝圆柱体按照正方形晶格周期排列在环氧树脂基体中构成的二维声子晶体作为分析算例,相关模型参数如表1所示。
取晶格常数a=0.01 m,为保证精度,取平面波数为625个,为方便问题的说明,本文采用带隙宽度ΔΩ=Ωmax-Ωmin及带隙中心频率Ωm=ΔΩ/2描述及对比不同形状散射体在正方形晶格内的带隙特性。
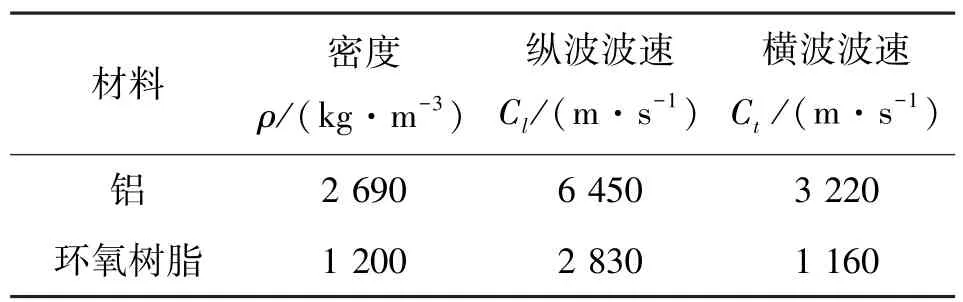
表1 仿真模型材料参数Table 1 Material parameters of simulation model
2.1 圆形散射体
首先,对圆形散射体采用表1中所示的相关数据,应用所建立的模型得到描述声子晶体带隙结构的特征值方程,求解特征值方程,得到如图2所示的能带结构图。
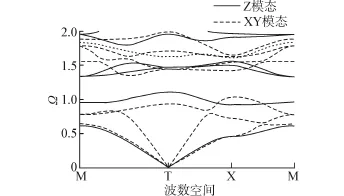
图2 圆形散射体二维声子晶体能带结构Fig.2 Band structure of 2-D phononic crystals with circle scatterers
本文所得到带隙曲线与文献[14]中对同样模型参数的计算结果基本一致,从而验证了本文理论建模和程序编制的正确性。根据图2可以明显地看出,经过测算,XY模态下最大正则化禁带宽度ΔΩmax为0.472 9,Z模态下最大正则化禁带宽度ΔΩmax为0.375 8。由于旋转角度对于圆形散射体不产生影响,故而不予探讨。
2.2 正方形散射体
对于正方形散射体,因存在结构的对称性,只用针对旋转角度θ由0向45°变化过程进行分析。首先对倒格子矢量依照式(14)进行转换,然后选取表1中的材料参数,依照所建立的理论模型形成特征值矩阵并求解特征值方程,得到声子晶体带隙结构图,记录禁带宽度及出现位置。
由图3可以看出,伴随着填充率的提高,禁带宽度呈现出先扩大后缩小的趋势,且在填充率很小时(f=0.1时)产生禁带宽度极小,且在该填充率下,当旋转角度超过25°时,禁带已经消失。在填充率小于或等于0.4时,伴随着旋转角度的增大,禁带宽度缩小,但是速度逐步减缓。当填充率大于0.4时,伴随旋转角度的增加,禁带宽度下降明显,且填充率越大,下降速率越快。

图3 不同散射体填充率条件下,正方形散射体禁带宽度与偏转角度关系图Fig.3 Relationship between rotation angle and gap width of square scatterers under various filling fractions
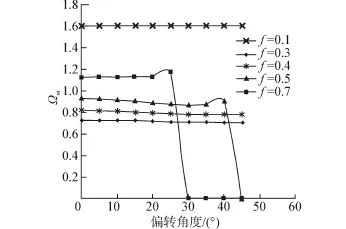
图4 不同散射体填充率条件下,正方形散射体禁带中间频率与偏转角度关系图Fig.4 Relationship between rotation angle and midgap of hexagon scatterers under various filling fractions
由图4可以看出,伴随着填充率的提高,禁带中间频率呈现逐步上升的趋势,即产生最大禁带的位置逐渐上升。当填充率等于0.1,结合图3可知,在前几阶特征频率下并没有禁带产生,在第8、9阶特征频率下有极窄禁带产生,且当旋转角度超过25°时,禁带基本消失。
图5为当填充率f=0.4时,旋转角θ分别为0及45°时Z模态下带隙结构图。
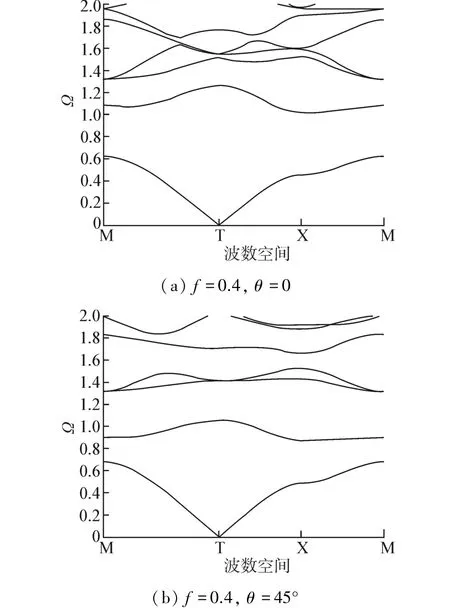
图5 正方形散射体Z模态禁带结构图Fig.5 Z mode of band gap of rectangular scatterers
2.3 正六边形散射体
由于正六边形散射体的对称性,取旋转角度θ范围在0~30°变化,分析过程同2.2节,得到声子晶体带隙结构图,记录禁带宽度及位置。如图6及图7所示禁带宽度及禁带中间频率都会产生显著变化。
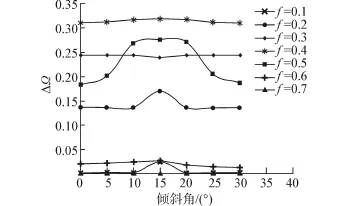
图6 不同散射体填充率条件下,正六边形散射体禁带宽度与偏转角度关系图Fig.6 Relationship between gap width of hexagon scatterers and rotation angle under various filling fractions
如图6所示,与正方形散射体的情况类似,伴随着填充率f的提高,禁带宽度总体呈现出先扩大再缩小的变化趋势。此外,当填充率过低或填充率过高时,禁带宽度较小,禁带宽度的变化也较小。伴随着填充率的上升,禁带宽度的变化也更加剧烈,当f>0.3时,禁带宽度均呈现出先扩大后缩小的趋势,且当旋转角θ=15°时,禁带宽度均达到最大值。
如图7所示,伴随着填充率f的提高,禁带中间频率总体呈现上升趋势,与正方形的情况相类似,伴随着旋转角度的增加,禁带中间频率较为固定,即禁带出现的位置较为固定。在实验过程中,也发现,无论填充率取到怎样的值,在旋转角θ=15°时,禁带出现的位置均有下降。

图7 不同散射体填充率条件下,正六边形散射体禁带中间频率与偏转角度关系图Fig.7 Relationship between midgap of hexagon scatterers and rotation angle under various filling fractions
图8 为当填充率f=0.5时,旋转角θ分别为0及15°时Z模态下带隙结构图。

图8 正六边形散射体Z模态禁带结构图Fig.8 Z mode of band gap of hexagon scatterers
2.4 椭圆形散射体
取椭圆短半轴与长半轴长度之比为aov∶bov=0.8∶1。分析过程如2.2所述,得到声子晶体带隙结构图,并记录禁带宽度及出现位置。
如图9所示,伴随着填充率f的提升,禁带宽度ΔΩ总体呈现逐步扩大的趋势。当填充率f较大时(f>0.5),伴随着旋转角度θ的上升,禁带宽度有着明显上升的趋势。但是当填充率f<0.5时,伴随着旋转角度的上升,禁带宽度呈现略微下降的趋势。
关于禁带产生的位置,如图10所示,伴随着填充率f的提升,禁带中间频率Ωm逐渐上升,当填充率f保持不变时,禁带中间频率稳定,不存在明显的变化。旋转角对于禁带中间频率(即禁带产生的位置)不存在明显影响。
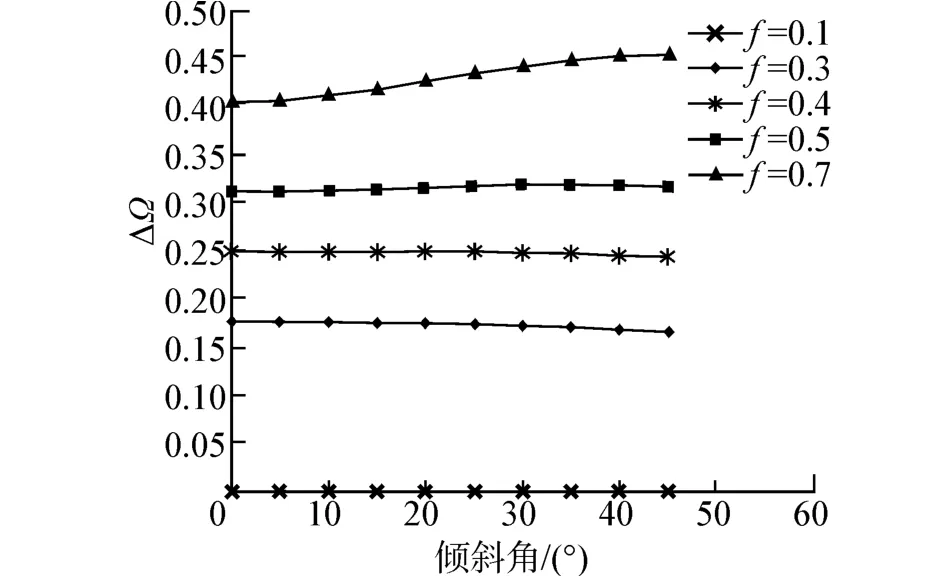
图9 不同散射体填充率条件下,椭圆形散射体禁带宽度与散射体偏转角度关系图Fig.9 Relationship between gap width of elliptical scatterers and rotation angle under various filling fractions

图10 不同散射体填充率条件下,椭圆形散射体禁带中间频率与散射体偏转角关系图Fig.10 Relationship between gap width of elliptical scatterers and rotation angle under various filling fractions
图11 为出现最大禁带宽度f=0.7,θ分别取0及45°时,其Z模态禁带结构图。

图11 椭圆形散射体Z模态禁带结构图Fig.11 Z mode of band gap of elliptical scatterers
3 结论
本文得到如下结论:1)散射体的旋转角对于禁带宽度具有显著影响。根据仿真结果可以看出,当散射体形状取为正方形时,在填充率固定的情况下,伴随着旋转角度的上升,禁带宽度总体呈现缩小趋势。但是当散射体形状取为正六边形时,同样在填充率固定的情况下,伴随着旋转角度的上升,禁带宽度总体呈现先扩大再缩小的趋势。2)散射体旋转角对于正六边形及正方形散射体的影响明显大于对于椭圆形散射体的影响。3)无论散射体取为何种形状,旋转角度对于声子晶体产生禁带的位置(禁带中间频率)影响并不明显。但较为明显的是,伴随着填充率的上升,最大禁带出现的位置都呈现上升趋势。
本文研究成果对于实际情况具有较好的指导意义,在实际应用中可以通过机械装置对散射体进行人为偏转,从而达到人为控制声子晶体带隙的目的。
[1]张荣英,姜根山,王璋奇,等.声子晶体的研究进展及应用前景[J].声学技术,2006,25(1):35-42.ZHANG Rongying,JIANG Genshan,WANG Zhangqi,et al.Progess of phononic crystal and the application perspectives[J].Technical Acoutics,2006,25(1):35-42.
[2]温激鸿,韩小云,王刚,等.声子晶体研究概述[J].功能材料,2003,34(4):1-3. WEN Jihong,HAN Xiaoyun,WANG Gang,et al.Review of phononic crystals research[J].Journal of Functional Materials,2003,34(4):1-3.
[3]SIGALAS M M,ECONOMOU E N.Elastic and acoustic wave band structure[J].Journal of Sound and Vibration,1992,158(2):377-382.
[4]KUSHWAHA M S,HALEVI P,ROUHANI B D.Acoustic band structure of periodic elastic composite[J].Phys Rev Lett,1993,71(1):2022-2025.
[5]MARTINEZ R S,SANCHO J,SANCHEZ J V,et al.Sound attenuation by sculpture[J].Nature,1995,378(1):241-248.
[6]KUSHWAHA M S,HALEVI P,MARTÍNEZ G.Theory of acoustic band structure of periodic elastic composites[J].Phys Rev B,1994,49(4):2313-2321.
[7]MESEGURE F,HOLGADO M.Rayleigh-wave attenation by a semi-infinite two-dimensional elastic-band-gap crystal[J].Physical Review B,1999,59(19):12169-12172.
[8]VASSEUR J O,DRYMIER P A,CHENNI B,et al.Experimental and theoretical evidence for the existence of absolute acoustic band gaps in two-dimensional solid phononic crystals[J].Physical Review Letters,2001,86(1):3021-3024.
[9]BERTODI K,BOYCE M C.Mechanically triggered transformation of phononic band gap in periodic elastomeric structures[J],Physical Review B,2008(77):052105.
[10]MULIN T,DESCHANEL S,BERTODI K,et al.Pattern transformation triggered by deformation[J].Phsical.Review Letter,2007(99):084301.
[11]BERTODI K,BOYCE M C.Wave propagation and instabilities in monolithic and periodically structured elastomeric materials undergoing large deformation[J].Phsical Review,2008(78):184107.
[12]YAN L,ZHAO H P,WANG X Y.Influence of scatterer's tropism on the band gaps of two dimension phononic crystal[J].Technical Acoustics,2006,25(6):608-612.
[13]WU F G,LIU Z Y,LIU Y Y.Acoustic band gaps created by rotating square rods in a two dimensional lattice[J].Phys Rev E,2002,66:046628.
[14]温熙森,温激鸿.声子晶体[M].北京:国防工业出版社,2009:61-68.
[15]王毅泽.磁电弹性声带隙材料中的弹性波传播与局部化研究[D].哈尔滨:哈尔滨工业大学,2009:18-32.WANG Yize.Elastic wave propagation and localization in magnetoelectroelastic band gap materials and structures[D].Harbin:Harbin Institute of Technology,2009:18-32.
[16]WANG R Z,WANG X H,GU B Y,et al.Effects of shapes and orientations of scatterers and lattice symmetries on the photonic band gap in two-dimensional photonic crystals[J].J Appl Phys,2001,90(9):4307-4313.
[17]赵言诚.二维声子晶体结构设计及其特性研究[D].哈尔滨:哈尔滨工程大学,2006:15-34.ZHAO Yancheng.Two dimensional phononic crystal design and its characteristics investigations[D].Harbin:Harbin Engineering University,2006:15-34.
Effects of the rotation angle of scatterers on the band gap structure of a two-dimensional phononic crystal
DU Jingtao,HE Yanbo,FENG Haocheng
(College of Power and Energy Engineering,Harbin Engineering University,Harbin 150001,China)
In order to investigate the influence of rotation of scatterers on the propagation characteristic of elastic waves in phononic crystals,the plane wave expansion method is utilized in this paper.The factor of rotation angle between scatterers and lattice axis is introduced into the structure function to explore the change of position as well as the width of the band gap structure for square,ellipse and hexagon scatterers corresponding to the change of rotation angle and filling fractions.The results demonstrated that the rotation angle of scatterers has significant impact on the band gap structure of two dimensional phononic crystals.In the meantime,such impact on the hexagon and square scatterers is more obvious than the elliptical scatterers.However,no matter what the shape of the scatterer is,the influence of rotation angle on the band gap position(mid-gap)of phononic crystals is not obvious.
phononic cyrstals;bandgap;forbidden band;rotation angles;plane wave expansion method;scatterers
10.3969/j.issn.1006-7043.201309069
http://www.cnki.net/kcms/doi/10.3969/j.issn.1006-7043.201309069.html
O481.1
A
1006-7043(2014)11-1358-06
2013-09-22.网络出版时间:2014-09-22.
国家自然科学基金资助项目(11202056).
杜敬涛(1981-),男,副教授,博士.
杜敬涛,E-mail:dujingtao@hrbeu.edu.cn.

