球杆系统的滑模变结构控制
郑艳伟,张井岗(太原科技大学电子信息工程学院,太原 030024)
球杆系统具备了非线性不稳定系统所有的动态特征,是典型的开环不稳定系统,也是一个验证各种先进控制算法具有代表性的实验平台。对其研究产生的控制算法和技术在机器人控制、军事领域和工业应用等方面都具有广泛的应用开发前景,所以对球杆系统这样的一个典型被控对象进行研究,无论在控制理论研究和工程实践中都具有重要的意义。
近年来国内外许多学者针对球杆系统提出了不同控制算法。如文献[1]提出了基于遗传算法的自适应PD控制,能使小球迅速的达到稳定位置;文献[2]采用网络化预测控制算法(NPC)设计了球杆网络化控制系统,通过实验证明相对于清空法和保持法,NPC可以使系统获得更好的控制效果;文献[3]针对球杆系统的非线性模型,分别提出了静态和动态基于等速趋近率的滑模控制;文献[4]提出了一种考虑驱动系统动态带有神经网络补偿的串级控制策略,基于常规的PD控制,将系统的闭环极点配置到期望的位置,最终实现了球杆系统的高精度控制;文献[5]针对球杆系统模型的不确定性,提出了一种自适应鲁棒控制策略;文献[6]设计基于插值的模糊控制器,使系统的控制性能得到进一步提高。
针对球杆系统,本文首先将其复杂的非线性模型进行线性化处理,其次针对简化的线性模型,基于指数趋近律设计滑模控制器;仿真和实验均表明:本文方法不仅能使小球较快的达到设定位置,而且具有较强的抗干扰能力,同时有效的削弱了滑模控制中存在的抖振现象。
1 球杆系统简介和数学建模
1.1 球杆系统简介
球杆系统的球杆装置机械结构示意图和组成示意图分别如图1和2所示。球杆装置主要包括大小齿轮箱减速机构、直流伺服电机、连杆、V型槽轨道。执行系统为不锈钢球和V型槽轨道。V型槽轨道两侧分别是直线位移电阻器和不锈钢杆。通过测量不锈钢杆上的输出电压可得球在轨道上的位置。计算机、线性传感器、IPM100智能伺服驱动器、光电码盘和球杆本体等几部分组成控制系统。控制器根据测量位置和目标位置之间的误差计算控制量,以及控制伺服电机转动减速齿轮角度θ,进而控制导轨与水平面的夹角α,最终使小球稳定到目标位置。
1.2 球杆系统的数学建模
由于完全描述小球运动的动态过程非常繁杂,本文对该控制系统给出一个相对简单的模型以便控制器的设计。
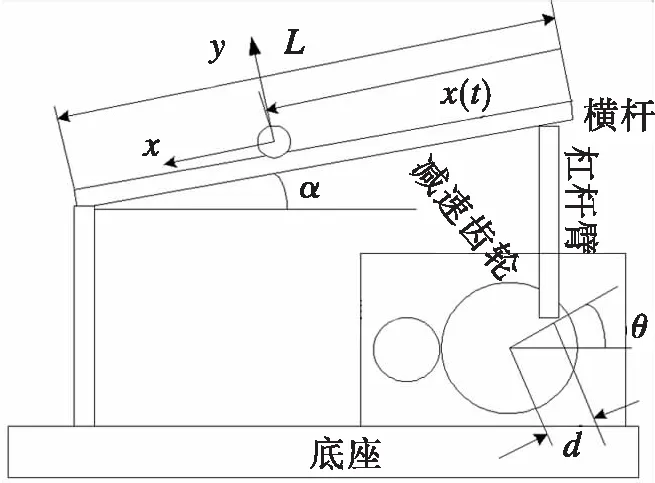
图1 球杆装置机械结构示意图
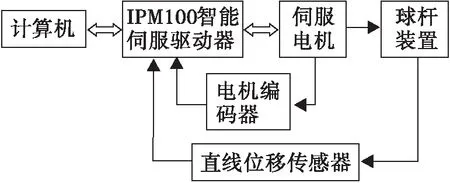
图2 球杆系统组成框图
小球在轨道上的受力为球受到的摩擦力和球的重力在平行与导轨方向上分力的合力。由小球的动力学方程可得小球在V型杆上的加速度表达式:
(1)
式中小球质量m=28 g;小球的转动惯量J=0.4mR2;小球半径R=14.5 mm;小球位置偏移r;重力加速度g=9.8 m/s;横杆偏角α;球杆长度L=0.4 m;杠杆臂与齿轮的连接点到齿轮中心的距离d=0.04 m.
由球杆机械结构知:
(2)
由于实际摩擦力较小,忽略摩擦力的影响,则小球运动的数学模型简化成下式:
(3)
当小球处于稳定位置时,α取值很小。当α<<1时,由sinα≈α,将式(3)线性化处理后,得到传递函数:
(4)
实际控制中,由电动机转角输出决定杆的仰角α.齿轮的减速比和非线性是电动机转角θ和杆仰角α之间关系的关键影响因素,对模型进一步简化得:
(5)
将式(5)代入式(4),可得简化模型为:
(6)
将参数带入,得系统的简化模型为:
(7)
2 球杆滑模变结构控制器设计
2.1 滑模变结构控制器设计
设计滑模控制器基本包括两个方面:滑模面s(切换函数)和控制量u(控制律)。滑模面一经选定,系统进入滑动模态后其动态响应只与滑模面参数相关而与扰动无关,继而可达到抑制扰动和参数摄动的效果。
对与单输入单输出的二阶系统:
(8)

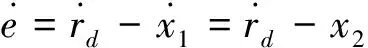
(9)
定义滑模函数如下:

(10)
为削弱系统的抖振,采用趋近律的控制方式,控制律推导过程为:

(11)
指数趋近律为:
slaw=-εsgn(s)-ksε>0,k>0
(12)
由式(8)、式(9)、式(11)得:
(13)
将式(12)带入式(13)得控制律:
(14)
对控制器进行稳定性分析,由式(11)和式(12)得:
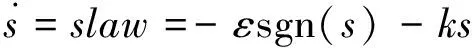
(15)
则有:
(16)
满足李雅普诺夫函数型的到达条件:
(17)
其中V(x)为定义的李雅普诺夫函数。
在式(14)所示的滑模控制律中,三个参数需要调整,即滑模面参数c,增益参数ε和趋近速度参数k.c是影响滑模运动稳定性和动态响应快慢的关键参数,参数k主要作用于切换函数的动态过渡过程。系统的快速性随着c和k的增加而变大,但过大的参数则会引起过大的控制量输出。ε的取值主要影响系统克服摄动及外界干扰,ε越大,系统克服摄动和外干扰的能力越强。但是,过大的增益则引起系统抖振加大。为了提高趋近效果同时削弱抖振现象,适当增大k而同时减小ε值。
2.2 球杆系统的滑模控制器设计
球杆系统的状态方程:
(18)
与式(8)中对应的g(x,t)=0,h(x,t)=0.7.
令控制器的状态变量为:
(19)
x1,x2为小球的位置,rd为小球位置的期望值,rd为常数,滑模面为:
将式(15)代入,得控制律:
(20)
本文用饱和函数sat(s)代替理想滑动模态中的符号函数sgn(s),这样能较好削弱滑模控制中抖振现象,基于式(20)则有:
(21)
MATLAB环境下以SIMULINK搭建球杆系统的仿真图进行仿真。将滑模控制器进行离散化,采样时间为0.02 s,球杆臂总长为0.4 m,取小球的期望置rd=0.25 m,在10 ms时加幅值为+0.05的阶跃干扰,参数选取c=0.000 2,ε=0.8,k=120时,系统的输出响应、滑模面和滑模控制器输出曲线分别如图3-5所示,由图3可以看出,本文方法可以使小球较快达到稳定位置,而且对外界干扰具有较强的抑制能力。
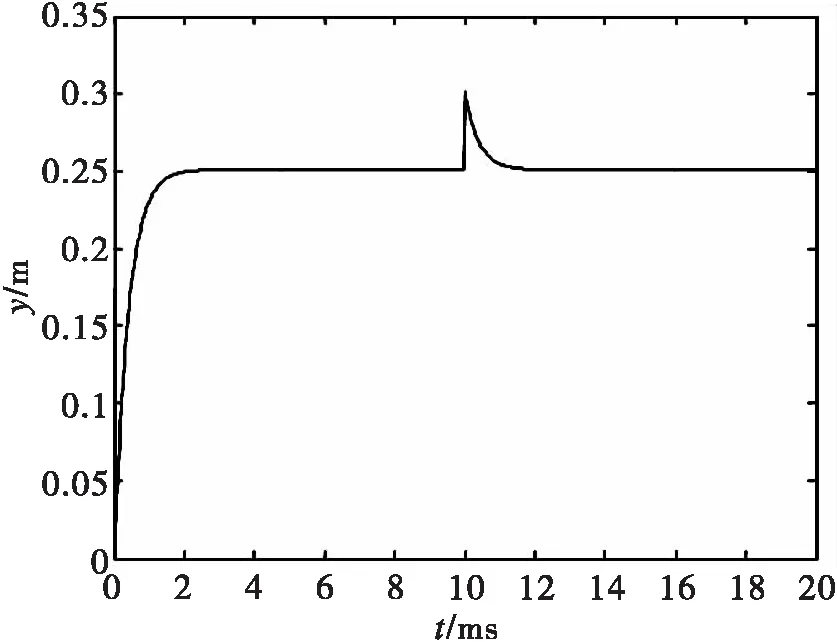
图3 滑模控制系统仿真曲线
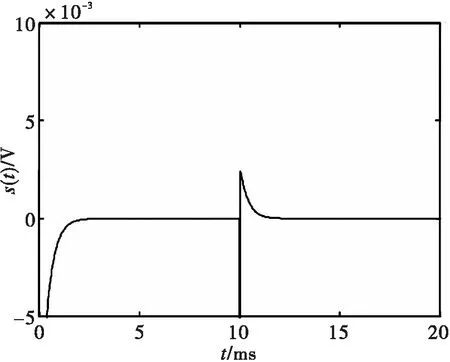
图4 滑模面仿真曲线
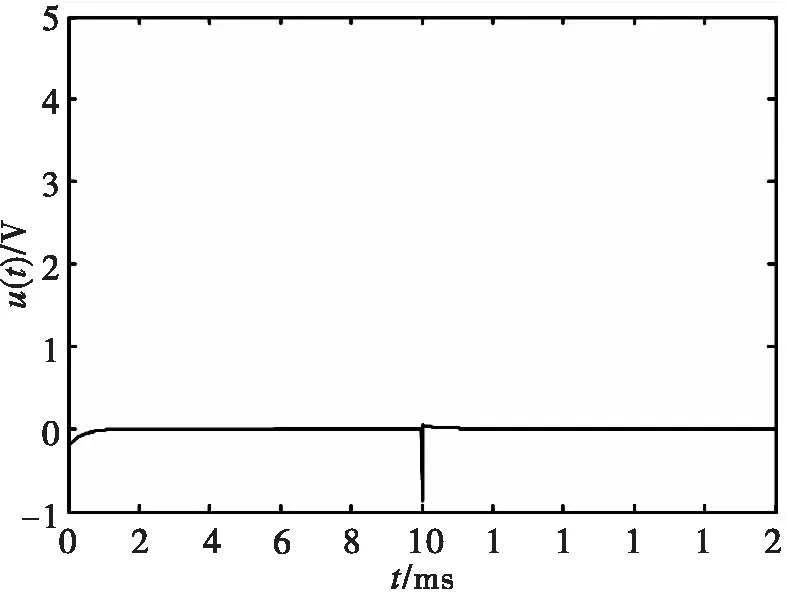
图5 滑模控制器仿真曲线
为验证本文方法在实际应用中的有效性,选用固高公司的GBB1004球杆系统进行实验控制研究。将滑模控制器进行离散化,采样时间为0.02 s.滑模控制器的参数选取为:c=0.02,ε=0.8,k=120.设定小球的期望值rd=0.25 m,在50 s时加幅值为+0.05的阶跃干扰,在Matlab/Simulink环境中进行实时控制,球杆系统实时控制界面为图6所示,其实验结果如图7-9所示。

图6 球杆系统实时控制界面
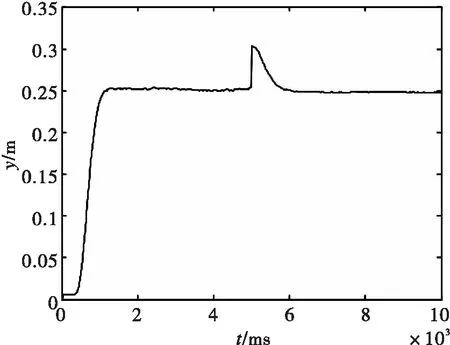
图7 滑模控制系统实时曲线
实时控制系统小球位置输出、滑模面输出和控制器输出曲线分别如图7-9所示,由图7可以看到,小球在10 s时稳定到期望值0.25 m,在50 s时加幅值+0.05的阶跃干扰,系统能较快的回到设定值。由图8和图9可以看出,有效的削弱了滑模控制中的抖振现象。仿真和实验效果验证了本文设计的基于指数趋近律滑模控制器可使小球快速,准确的稳定回到目标值,并且具有较强的抗干扰能力。

图8 滑模面实时曲线
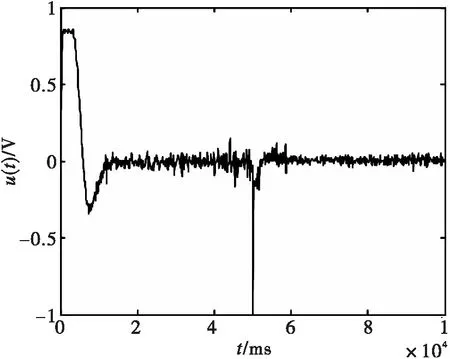
图9 滑模控制器实时曲线
3 结论
本文针对球杆系统,首先对复杂的非线性模型进行线性化简化处理,其次设计出基于指数趋近律的滑模控制器。仿真和实验结果表明该方法可使小球具有较好的动态响应性能,并且对外界具有良好的干扰抑制能力,同时有效的削弱了滑模控制中引起的抖振现象。
参考文献:
[1] 刘克平,史鹏飞.球杆系统自适应遗传PID控制[J].控制工程,2009,16(2):173-175.
[2] 罗浩铭,刘国平,桂卫华.球杆系统的网络化控制设计与实现[J].控制工程,2011,18(5):688-691.
[3] ALMUTAIRI NAIF B,ZRIBI MOHAMED.On The sliding mode control of a Ball on a Beam system[J].Nonlinear Dynamics,2010,59(1-2):221-238.
[4] 侯俊,王良勇,柴天佑,等.球杆系统的基于神经网络补偿的串级控制[C]∥World Congress on Intelligent Control and Automation,China,Jinan:2010.
[5] YANG J,WANG Z.Adaptive robust dissipative design on stability control for ball and beam system[J].IEEE,2010,4:68-71.
[6] 唐德旺,王庆林.球杆系统模糊控制的研究[C]∥Proceeding of the 27thChinese Control Conference,China,Yunan:2008.
[7] 胖永新,金迪,孟宪东.球杆系统的建模、仿真与控制器设计[J].武汉大学学报:工学版,2005,38(6):142-146.
[8] OH SUNGKWUN,JANG HANJONG,PEDRYCZ WITOLD.The design of a fuzzy cascade controller for ball and beam system:A study in optimization with the use of parallel genetic algorithms[J].Engineering Applications of Artificial Intelligence,2009,22(1):261-271.
[9] 陈志梅,王贞艳,张井岗.滑模变结构控制理论及应用[M].北京:电子工业出版社,2012.
[10] 刘金琨.滑模变结构控制MATLAB仿真[M].北京:清华大学出版社,2005.

