BP神经网络优化网络科技文献共享评价体系
冯世杰,谭 瑛,王 艳(太原科技大学复杂系统与计算智能实验室,太原 030024)
评价自古以来就广泛存在于人们的社会生活中[1],到了近代,随着社会生产力的快速发展,物质及精神文明高度丰富,人们在长期的实践评价中形成了百余种的评价方法和评价理论[2]。
评价指标体系是评价的基础,是根据评价对象的各个方面的特征以及之间的相互关系定义多个多层指标。如何对构建的指标体系进行优化,避免人为的情感干扰,使之更加科学合理,成为现在研究的热点。传统的优化方法(德尔菲法、主成分法等),主要还是凭借专家的经验及感受,并且数据量小,使得评价结果具有一定的不稳定性。而BP神经网络方法是神经网络中成熟且应用广泛的方法,其非线性拟合及联想记忆功能强使其在优化评价指标体系中具有一定的先进性,目前BP神经网络方法还没有在优化网络科技文献共享评价指标体系上得到应用。本文的实例应用也是对网络科技文献共享方面评价的创新。
1 研究对象及指标构建
本文是从网络科技文献共享方面进行研究。自从进入知识经济时代,日益增加的科技信息量和人们对科技信息的有效获取成了不可避免的一对矛盾。而网络科技文献共享平台就作为科技文献资源的载体为人们拥护提供方便、快捷的科技文献资源,极大的满足了人们对科技文献资源的需求。科技文献以共享机制为核心的网络平台建设在政府的大力支持下,在近些年得到了长足的发展,取得了显著地成绩,但是作为公共财政投资建设的共享平台,以往对的评估监测大多处于自我评价状态,评估结果很难做到客观公正。随着互联网技术的广泛应用和普及,其所具有的开放性和公众参与性,使得从第三方角度对网络科技文献共享程度进行公正科学的评估成为可能。本文以各省、市地方科技信息研究所的科技文献共享为对象,构建指标。
首先通过文献的调阅、小组讨论以及对专家学者请教访问,列出评价的指标,其次按照评价指标的构建原则、构建内容和构建程序进行归纳综合,得出一个三层指标的指标结构,初步形成网络科技文献共享的评价指标结构[3-4],如图1所示。
2 指标体系的主要评价方法
目前国内外常用的指标体系评价方法有德菲尔法(Delphi)[5]、主成分分析法(Principal Component)[6]、模糊综合评判法[7]、灰色系统评价法[8]、层次分析(AHP)法[9]、数据包络分析法(DEA)[10]、人工神经网络 (ANN)[11]等。

图1 网络科技文献共享评价指标初选
德尔菲法是一种主观、定性的方法,通过多次多轮专家对问卷问题的看法,经过反复的征询、反馈和归纳,汇成基本一致的看法。此方法可以充分反映人们对评价对象的感性的认识,得出具有直接性和可理解性的结果。但是由于依靠评价者的主观判断加上调查评价周期较长以及参评人员价值偏向等问题,容易使评价出的结果可靠性较低。
主成分法是把给定的一组组相关变量通过线性变换转成一组不相关的变量,在总方差不变的情况下,新的变量按照方差依次递减的顺序排列。由于这种对数据的相关性判断不能代表对指标的价值判断,所以常出现一些错误,使其不能解决实际问题。
模糊综合评价法是一种基于模糊数学的综合评价方法。该方法根据模糊数学的隶属度理论把定性评价转化为定量评价,即用模糊数学对受到多种因素制约的事物或对象做出一个总体的评价。它具有结果清晰,系统性强的特点,能较好地解决模糊的、难以量化的问题,适合各种非确定性问题的解决。
灰色系统评价法是对系统中所包含的相互联系、相互影响、相互制约的指标之间,在发展过程中,其同步(或同向)变化的程度进行比较的一种定量研究方法。它可以反映各因素随时间而演变的动态关系,可以理顺与分清系统中因素的“主次”或“亲疏”关系,为进一步阐明系统发展过程的主要特征和客观规律提供科学依据。
层次分析法是指将一个复杂的多目标决策问题作为一个系统,将目标分解为多个目标或准则,进而分解为多指标的若干层次,通过定性指标模糊量化方法算出层次单排序和总排序,以作为多指标、多方案优化决策的系统方法。层次分析法的特点是在对复杂的决策问题的本质、影响因素及其内在关系等进行深入分析的基础上,利用较少的定量信息使决策的思维过程数学化,从而为多目标、多准则或无结构特性的复杂决策问题提供简便的决策方法。该方法比较适合于具有分层交错评价指标的目标系统,而且目标值又难于定量描述的决策问题。
数据包络分析法是一种用来对一组具有多输入和多输出的决策单元的相对效率进行评价的数学规划方法。该方法以相对效率为基础,根据多指标投入与多指标产出对相同类型的决策单元进行相对有效性评价。
人工神经网络是一整套简化、抽象、模拟人脑功能的极其复杂的非线性动力学系统,它是在现代神经科学研究成果的基础上提出的,通过模拟大脑神经网络的功能及结构的若干基本特征,依靠着系统的复杂性以及通过调整内部各节点之间的相互关系,来达到模仿众多的神经元达到模仿人脑对信息的处理能力,人工神经网络法为非线性系统的指标优化提供了一种有效的方法。它是以核心指标作为网络输出,其他因素指标作为网络输入,通过网络来刻画出输入和输出之间的相关性。这种方法可以合理地选择需要的指标变量,排除不合理指标变量,其建模过程可以大为简化,精度也有较大的提高。
3 BP神经网络简介
根据上述对各种主流方法的简介,采用比较新型、人为干扰小、建模简便及计算精度高的人工神经网络作为优化评价指标体系的建模工具。
BP神经网络[12]作为众多神经网络中应用最多和成熟的神经网络算法,是RumeChart等人1985年在反向传播算法的基础上发展起来的,是一种多层次反馈型网络,是有导师学习算法,它的学习过程有正向传播与误差的反向传播组成的。输入样本从输入层输入,经过隐层逐层处理,传向输出层。若输出与期望的结果不符,则将误差以某种形式通过隐层传向输入层,并分摊给各层神经元,此时误差将作为修正单位权重的依据,不断调整各单位误差,直至输出的误差减少到规定的范围内[13]。网络结构如图2.

图2 BP神经网络结构
BP神经网络的学习算法步骤[14]:
(1)设置初始参数w和θ(w为初始权值,θ为临界值,均为随机较小的数);
(2)将样本数据加到网络上,利用一下公式计算网络输出;

(1)
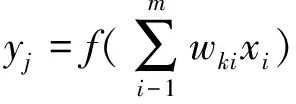
(2)
上述一式中f(x)为单极性Sigmoid函数,二式为纯线性purelin函数;i、j、k分别为神经网络的输入、输出和隐层单元,m、p分别为输入和隐层神经单元数;wki、wjk分别为输入神经元i到隐含神经元k的链接权和输出神经元j到隐含神经元k的链接权;
(3)各层权值的调整
调整量: △w=ηδjyj
(3)
其中,η为比例系数,即学习率,在计算中一般设置为[0,1]区间上一个较小的数;xj在隐节点为网络输入,在输出节点则为隐节点的输出;dj为期望输出数据;δj是一个与输出偏差相关的值,即(dj-yj);
对于输出节点:
δj=ηj(1-yj)(dj-yj)
(4)
对于隐层节点有:
(5)
其中k指要把上层(输出层)节点取遍,误差δj是从输出层反向逐层计算的;
各层神经元调整后的权值为:
wki(t)=wki(t-1)+△wki
(6)
其中t为学习次数,这个算法是个迭代过程,每一轮将各神经元间的权值调整一遍,这样一直迭代下去,直到输出误差小于某一允许范围为止。
4 应用分析
发放调查表收集样本数据,问卷的评分是根据每个指标对上一级指标影响的重要程度进行打分,除去残缺及具有明显个人不认真等不合格的数据样本,本文选取55为学者(研究人员)的打分作为样本数据。其中50人的打分数据作为训练样本,5人的打分数据作为测试样本。
总体优化方法,首先构建神经网络模型,其主要是根据指标体系结构和多少来确定神经网络结构及模型的训练参数;其次是训练专家学者打分的数据样本,得到稳定的训练结果;最后根据各个神经元间的链接权值求取各项指标的权重,得知各个指标在整个指标体系中的价值,进而优化初选的指标体系。具体步骤如下:
4.1 确定神经网络结构
本次优化采用三层BP神经网络进行训练,即为输入层、输出层、隐含层。输入为三级指标,输出为一级指标,由于三级指标数较多,优化分为三个模型进行样本训练,即一个一级指标对应下面的三级指标。隐含层是自行设定的,一般来说,问题越复杂需要的隐含层单元数就越多,但是过多的隐含层单元又会增加网络训练的计算量,影响训练效能,所以根据经验递减实验的方法来确定隐含层单元的个数。网络模型参数如表1.
4.2 网络训练参数确定
确定神经网络模型的基本训练参数如表2.
4.3 训练网络模型
对三级指标的打分作为网络的输入数据,一级指标的打分为网络的输出。应用Matlab软件编写程序[15-16],运行程序,得出神经网络的训练结果。由于有三个一级指标对应三级指标,需要三次训练求取各指标权重,方法是一样的,所以本文以“三级指标2”为例对可得性下的各个指标权重进行求取。训练误差变换如图3.

表1 神经网络模型参数

表2 神经网络训练参数

表3 三级指标2网络训练各神经元链接系数
4.4 指标权重的确定
表3中的数据只是反映了各个神经元之间的权重(链接权),如要求取各个输入指标对输出指标的真实关系,还需对神经元间的连接权值加以分析处理[17-18].
A、显著性系数:

(7)
B、相关系数:
Rij=|(1-e-y)/(1+e-y)|
y=rij
(8)
C、绝对影响系数:
(9)
i、j、k分别为神经网络的输入、输出和隐层单元,m、p分别为输入和隐层神经单元数;wki、wjk分别为输入神经元i到隐含神经元k的连接权和输出神经元j到隐含神经元k的链接权。
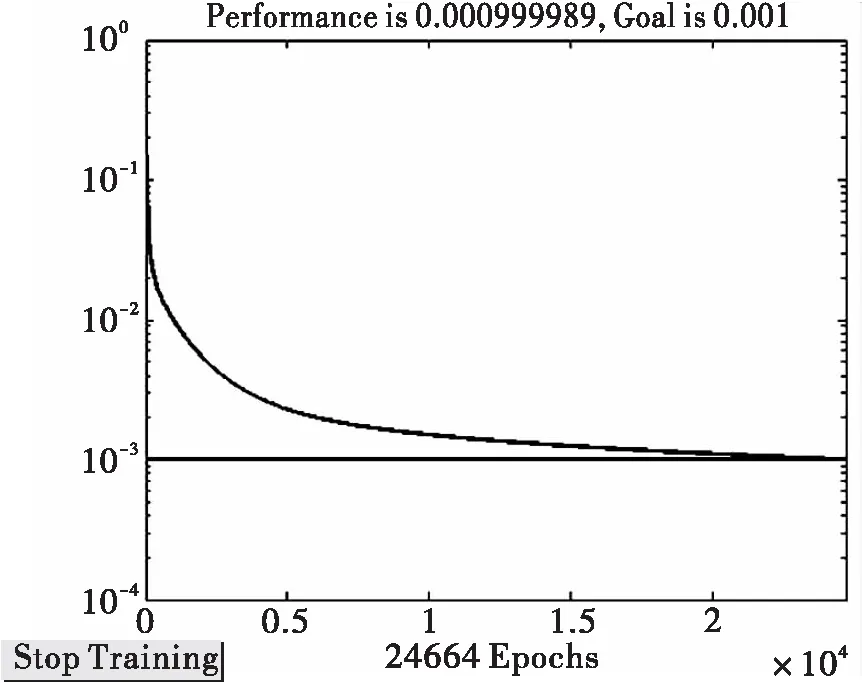
图3 BP神经网络训练误差变换
4.5 计算指标权重
根据公式7-9,计算出各个三级指标的权重如表4.
5 总结
利用BP神经网络方法来确定各指标的权重,可以清晰的看到各项指标在整个指标体系中的价值,从而优化改善指标初选指标,确定最终的网络科技文献共享评价指标体系。从上述权重表中可以得知,获取费用适度性指标在整个指标体系中所占的非常小,可以去除或进行替换。
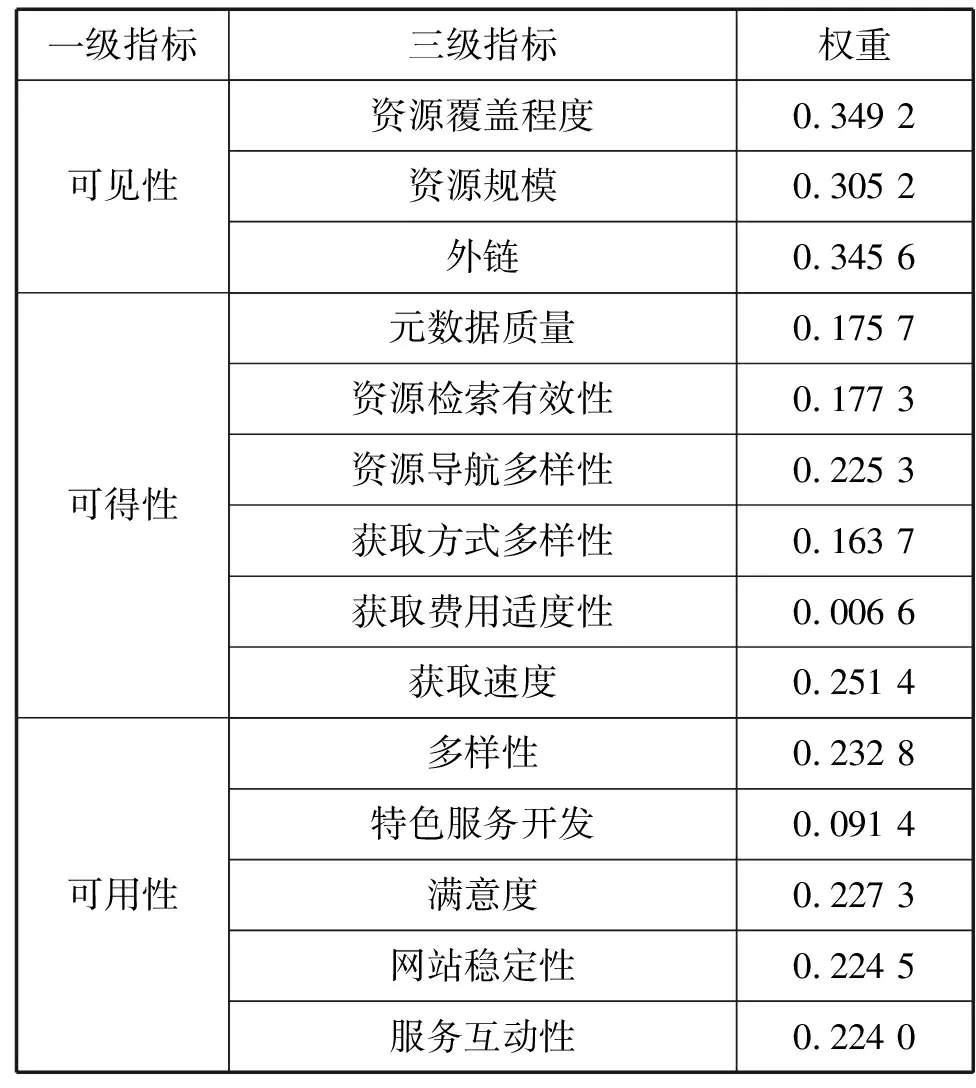
表4 三级指标的权重
任何方法都不是万能的,神经网络也不例外。随着社会的发展和样本基数的增多,神经网络模型的结构会越来越复杂,训练的效率也会降低。陷入局部最小值和样本数据过于复杂使训练难以收敛到要求的误差范围之内,因此单纯的BP神经网络就不能满足评价需要。这就需要和其他一些算法[19]进行结合应用(如遗传、粒子群等),目前应用粒子群(PSO)与BP神经网络结合的算法[20]来训练,能较大的提高训练的效率。
参考文献:
[1] 苏为华.多指标综合评价理论与方法研究[M].北京:中国物价出版社,2001.
[2] 王雪铭.评价方法的演变与分类研究[D].上海:上海交通大学,2009.
[3] 刘 仁,卞树檀,于强.评估指标体系构建的方法研究[J].计算机设计工程,2013,21(1):34-40.
[4] 蔡晶波.政府网站的服务性指标体系研究[D].长春:吉林大学,2013.
[5] CHRISTINA SEGERHOLM.Researching Evaluation in National (State)Politics and Administration,A Critical Approach[J].American Journal of Evaluation,2003,24(3):353-372.
[6] 王根蓓,赵晶,王慧敏.中国服务外包基地城市竞争力的演化-基于主成分方法的实证分析[J].经济与管理研究,2011(1):23-26.
[7] 叶俊杰,刘业政.采用模糊C均值聚类改进模糊综合评判模型[J].计算机工程与应用,2011,47(16):33-36.
[8] 张渊渊,何佳,贾海云.改进的灰色系统理论在汇率预测中的应用[J].计算机仿真,2011,28(11):21-24.
[9] GUISSEPPI A.Forgionnea,Rajiv Kohlib,Darniet Jenningsa.An AHP analysis of quality in AI and DSS journals[J].Omega,2002,30:171-183.
[10] 王婷,赵建.基于DEA/AHP混合模型的业务流程再造绩效评价研究[J].北京理工大学学报,2010,30(11):389-394.
[11] 刘天舒.BP神经网络的改进研究及应用[D].哈尔滨:东北农业大学,2011.
[12] 张乃尧,阎平凡.神经网络与模糊控制[M].北京:清华大学出版社,1998.
[13] 韩力群.人工神经网络理论、设计及应用[M].北京:化学工业出版社,2002.
[14] 魏海坤.神经网络结构设计的理论与方法[M].北京:国防科技大学,2005.
[15] 傅荟璇,赵 红.MATLAB神经网络应用设计[M].北京:机械工业出版社,2010.
[16] 葛哲学,孙志强.神经网络理论与MATLABR2007实现[M].北京:电子工业出版社,2007.
[17] 孙会君,王新华.应用人工神经网络确定评价指标的权重[J].山东科技大学学报,2001,20(9):84-86.
[18] 唐荣江.车内品质预测与控制技术研究[D].长春:吉林大学,2013.
[19] 曾建潮,崔志华.自然算法[M].北京:国防工业出版社,2012.
[20] 刘希玉,刘 弘.人工神经网络与微粒群优化[M].北京:北京邮电大学出版社,2008.

