摇摆对单相强迫循环流量波动特性的影响机理
幸奠川,阎昌琪,孙立成
(哈尔滨工程大学核安全与仿真技术国防重点学科实验室,黑龙江哈尔滨150001)
摇摆对单相强迫循环流量波动特性的影响机理
幸奠川,阎昌琪,孙立成
(哈尔滨工程大学核安全与仿真技术国防重点学科实验室,黑龙江哈尔滨150001)
针对摇摆条件下的单相强迫循环流量瞬变特性开展流量波动影响机理研究。通过调节离心泵转速、阀门状态及摇摆参数分析驱动压头、回路阻力及附加压降对流量波动幅值的影响。通过建立摇摆条件下单相流量波动方程,系统地揭示摇摆运动的影响机理.结果表明,增加驱动压头和回路阻力使得相对流量波动幅值减小,增加附加压降使得相对流量波动幅值增大。当驱动压头大于附加压降幅值的10~11倍时,摇摆对单相强迫循环流量波动的影响可忽略。流量波动方程分析结果与流量波动实验结果有很好的一致性。
摇摆运动;强迫循环;流量波动;驱动压头;理论模型;影响机理
受海浪冲击、海风等海洋条件的影响,船舶在运行中会伴随摇摆、起伏和倾斜等多自由度附加运动[1-4],动力装置内冷却剂流动所遵循的规律和陆基反应堆不同。鉴于摇摆条件下流动与传热的复杂性及实际工程应用的特殊性,需借助于摇摆台进行热工水力实验[1-9]。
由于实验条件不同,目前,摇摆条件下单相强迫循环流量是否周期性波动存在争议。文献[1-3]表明摇摆条件下单相强迫循环流量不波动。文献[5-7]实验结果表明,摇摆运动会导致流量显著波动,波动周期等于摇摆周期,波动幅值与摇摆周期、摇摆振幅及平均流速有关。近期实验结果表明,摇摆条件下流量是否周期性波动与驱动压头相对大小有关[8-9]。目前,学术界尚未对摇摆条件下单相流量波动特性相关文献进行系统总结,理论分析模型没有考虑不同驱动压头下的流量波动特性,摇摆运动影响单相流量波动幅值的机理尚不明确。因此,本文对前期研究进行系统的总结,结合一维流量波动分析模型,揭示摇摆运动对单相强迫循环流量波动的影响本质,获得摇摆运动对单相强迫循环产生明显影响的临界驱动压头,对开展摇摆条件下热工水力实验和工程设计都具有十分重要的意义。
1 流量波动方程
摇摆条件下单相绝热流动一维动量守恒方程为[10]

式中:Lv,j、Aj和W分别为第j段控制体的长度、流道面积和回路质量流量;Δpdri、Δpa和Δpresi分别为离心泵驱动压头,回路总附加压降及回路总流动阻力。回路总附加压降可按文献[10]计算得到
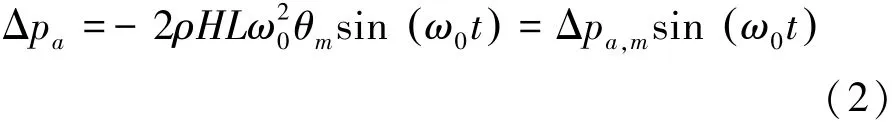
式中:ρ、ω0、θm分别为水密度、摇摆圆频率和摇摆振幅,H和L为实验回路高度和宽度。
摇摆条件下回路总流动阻力为
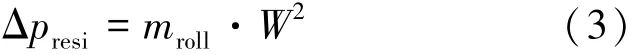
式中:mroll为摇摆条件下回路有效阻力系数。摇摆运动起始前回路总阻力应与驱动压头相等,即

式中:m0为竖直工况总阻力系数;W0为稳定状态下质量流量。摇摆条件下回路流量周期性波动时总阻力略大于稳定状态,从而导致平均流量比稳态略小[9]。因此,摇摆条件下回路总阻力系数应表示为

式中:ζ为摇摆条件下阻力修正因子,其取值与摇摆工况及平均流速有关,本文暂取1≤ζ≤1.08。
定义摇摆条件下相对流量为瞬时流量与摇摆起始前的稳定流量之比,Wrel=W/W0,则摇摆条件下流量波动方程可整理成:

式中:d1=Δpcl/W0∑Lv,j/Aj()为稳定项系数,对于确定的回路,d1表示驱动压头与初始流量的相对大小;d2=2ρlHLω20θm/W0∑Lv,j/Aj()为波动项系数,表示附加压降幅值与初始流量的相对大小。式(6)右端含有相对质量流量的平方项,为一阶非线性常微分方程,本文采用四阶Runge-Kutta方法对其进行求解,时间步长取为0.05 s,以T=10 s为例。
阻力修正因子ζ取值不同时的计算结果见图1。ζ越大,即摇摆引起的回路总阻力增加越明显,相应的回路平均流量越小,相对流量曲线整体向下平移。海洋条件下的实验参数范围内,ζ变化幅度很小,不会引起相对流量波动幅度的较大改变,见图1。因此,本文分析相对流量波动幅值时重点关注稳定项系数和波动项系数的影响。
图2表明,摇摆条件下相对流量周期性波动幅值随稳定项系数(d1)与波动项系数(d2)的比值的增加而迅速减小,当d1=10d2时,相对流量波动幅值小于5%,可近似认为摇摆运动的影响可忽略。前文指出海洋条件下阻力修正因子对瞬时流量波动幅值的影响有限,对确定的回路,初始流量相同时稳定项系数和波动项系数分别由驱动压头和附加压降决定。因此,有效驱动压头大于附加压降幅值的10~11倍[Δpdri>(10~11)Δpa,m],可作为摇摆运动对闭合回路单相瞬时流量无明显影响的判断标准。

图1 阻力修正因子比较Fig.1 Comparison of the modified resistance factor
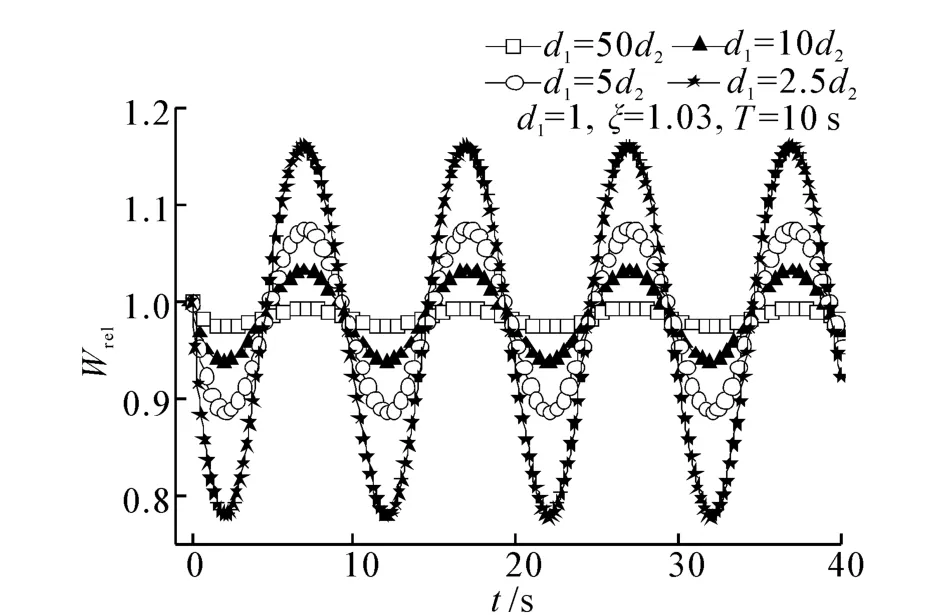
图2 瞬时流量计算值Fig.2 The calculated transient flow rate
2 实验装置
摇摆台及实验回路见图3。摇摆台由曲柄连杆机构驱动,绕中心轴做简谐摇摆运动,其运动规律及运动原理见文献[4-6]。实验回路垂直于摇摆台,见图3。离心泵驱动电机通过变频器供电,调节电机输入频率可获得不同的驱动压头。流量计量程0~2 m3/h,精度为0.1级;实验段进出口温度采用N型铠装热电偶测量,最大误差0.5℃。以上参数采用计算机采集系统动态监测和记录,采样频率为9 Hz。摇摆参数范围:摇摆振幅为10°、15°和20°;摇摆周期为10、15和20 s。
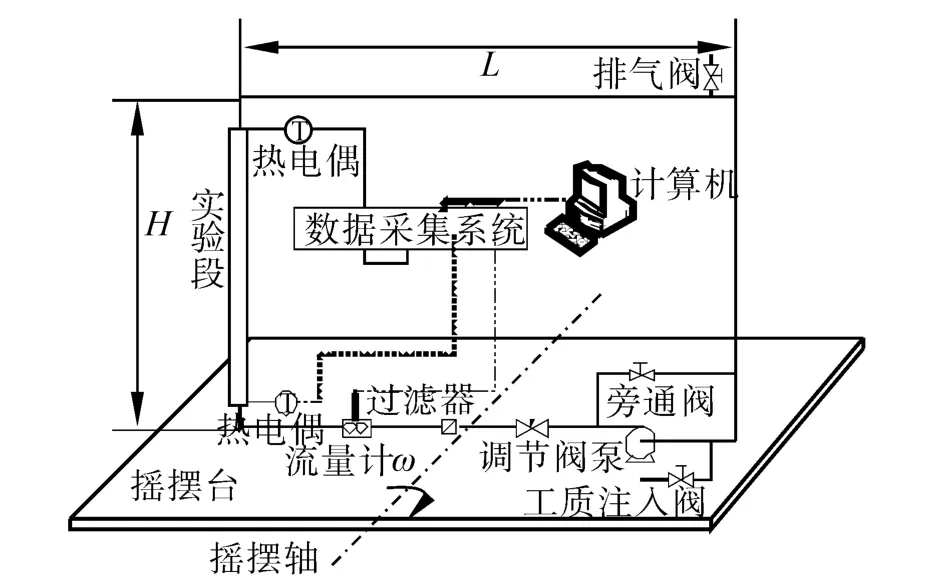
图3 摇摆台及实验回路示意图Fig.3 Schematic diagram of the rolling platform and experimental loop
3 实验结果分析
实际实验中,改变稳定项系数(d1)常通过调节阀门开度和离心泵转速2种方式实现,波动项系数(d2)常通过改变摇摆周期和摇摆振幅2种方式实现。
3.1 改变回路阻力
恒定的驱动压头下减小调节阀开度时,回路总阻力增加,从而引起初始流量减小。按照这种流量调节方式获得的摇摆条件下相对流量波动曲线见图4(a)。显然,保持驱动压头及附加压降不变时,减小阀门开度使得相对流量波动幅值迅速减小。实验中观察到减小阀门开度使得流量波动幅值及平均流量均迅速减小,且前者变化速率更快,因此,相对流量幅值随调节阀开度增加而减小。
采用调节阀门开度的方式改变流量时,摇摆运动对单相强迫循环流量波动幅度的影响还可从循环泵特性曲线结合回路阻力特性曲线来分析。摇摆条件下总阻力为

其中,下标kk为第kk个设定调节阀开度工况。摇摆条件下管路阻力特性曲线为位于mrollW2-d2和mrollW2+d2之间的曲线族。随着调节阀开度的减小,式(7)中的mroll增加,相应的阻力特性曲线族斜率变大,见图4(b)。阻力特性曲线族变陡后与泵特性曲线相交的范围变小,即泵的工作点变化范围随阀门开度减小而减小。因此,流量波动幅度随阀门开度减小而迅速降低。泵运行特性分析结果和实验结果有很好的一致性。
实际海洋条件下流动阻力特性实验中,往往采用固定驱动压头不变,改变调节阀开度的方式来改变回路流量,见文献[7]。由第1节中流量波动方程可知,这种实验方案在改变稳定项系数的同时,引起了波动项系数的改变,而驱动压头和附加压降幅值都没有变化,不适合用于探索摇摆运动对单相流量波动产生明显影响的判据。
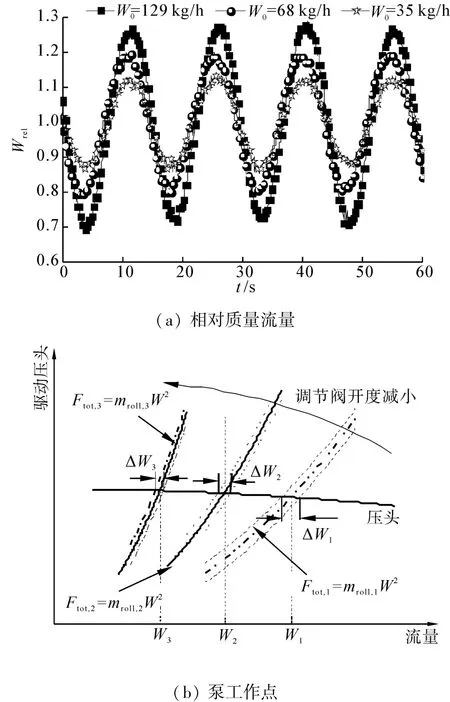
图4 调节阀门对流量波动的影响Fig.4 Effects of regulating the valve on flow fluctuation
3.2 改变驱动压头
阀门开度不变的条件下增加驱动压头,对应的初始流量增加。早期研究中曾采用这种实验方案调节流量[5-6],相应的流量波动曲线见图5(a)。这种流量调节方式下,增加初始流量引起实际流量波动幅值略微减小,但总体上变化不大,主要引起回路平均流量大幅增加,因此,相对流量波动幅值随驱动压头增加而明显减小。
按照调节循环泵压头的方式调节流量时,回路特性曲线并无明显改变,见图5(b)。提高驱动压头使得泵运行点变化范围略有减小,但总体上变化不大,相应的流量波动幅值变化也很小。另外,由第1节中流量波动方程可知,增加驱动压头使得稳定相系数大幅增加,从而使得相对流量波动幅值迅速减小。
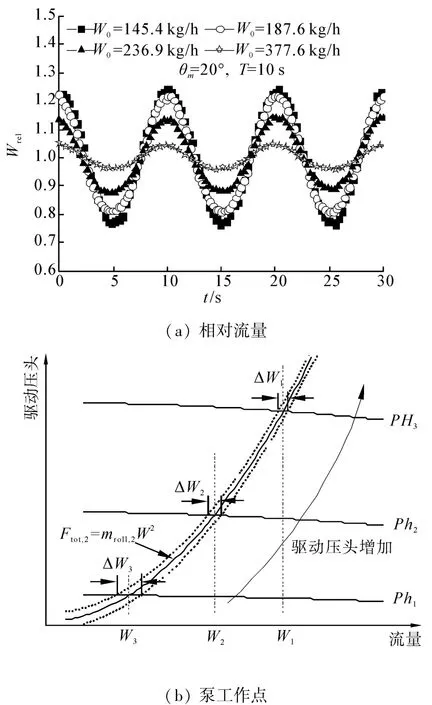
图5 调驱动压头对流量波动的影响Fig.5 Effects of regulating the pressure head on flow fluctuation
以上分析表明:增加回路阻力和驱动压头均能使相对流量波动幅值迅速减小。但这2种实验方案都引起了初始流量的改变,使得流量波动方程中稳定项系数具有不可预测性,不便用于探索判断摇摆运动影响单相流量波动特性的边界。
3.3 改变摇摆参数
波动项系数(d2)主要与摇摆参数、回路结构和初始流量有关。对于确定的回路和相同的初始流量,波动项系数主要受附加压降幅值影响,取决于摇摆周期和摇摆振幅。保持其他参数不变,摇摆振幅和摇摆周期对相对流量波动幅值的影响见图6。显然,摇摆条件下相对流量周期性波动幅值随摇摆振幅增加而增大,随摇摆周期减小而增大。增加摇摆振幅和减小摇摆周期,都会导致回路总附加压降幅值增加,也就是引起式(6)中波动项系数的增加,一维流动理论分析结果再次得到验证。本节建立的一维流动模型可用于摇摆条件下实验回路布置计算和实际工程参考,提出的流量波动影响因素分析方法可推广到任意周期性脉动流系统中。
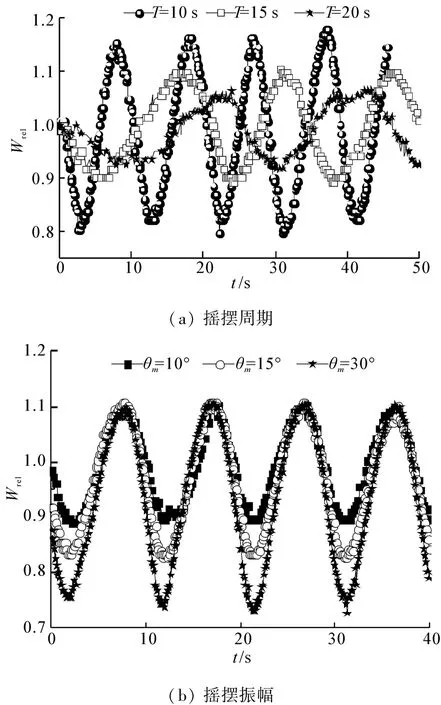
图6 摇摆参数对相对流量波动幅值的影响Fig.6 Effects of rolling parameters on fluctuation amplitude of the relative flow rate
3.4 临界驱动压头
实际实验中,保持初始流量不变的情况下增加驱动压头需减小阀门开度。不同驱动压头下实验测得的相对流量曲线见图7。显然,初始流量不变的条件下,相对流量波动幅值随驱动压头增加而迅速降低。当驱动压头为Δpdri=19.1 kPa时,对应的流量波动幅值小于其平均值的5%,可近似认为此时摇摆条件下流量无明显的周期性波动现象。此时附加压降幅值为Δpa,m=1 812 Pa(θm=20°,T=10 s),即Δpdri>10.5Δpa,m时,摇摆运动对单相流量波动的影响可忽略,本节实验结果很好的验证了理论模型分析结果。
调泵与调阀相结合的方式相当于回路阻力特性曲线和驱动压头同时改变,以保证初始流量恒定,对应的泵运行特性曲线见文献[8]。回路阻力特性曲线族斜率的增加使得其与驱动压头相交的范围减小,即泵运行点范围缩小,相应的流量波动幅值变小。由于初始流量恒定,相对流量波动幅值也呈减小趋势。

图7 相同初始流量下相对流量波动Fig.7 The fluctuation of the relative flow rate for the same original flow rate
由于实验条件的不同,学术界关于单相流量是否周期性波动存在争议,本节驱动压头和附加压降的相对关系可合理解释文献中的不同实验结果。文献[1-3]采用高扬程离心泵驱动,其压头远大于附加压降,相应的流量不波动。文献[5-6]采用调节循环泵转速的方式调节流量,小流量时对应的驱动压头低,流量呈明显的周期性波动;大流量时驱动压头大于附加压降幅值的10~11倍,流量不波动。文献[7]小流量时采用高位水箱提供压头,驱动压头相对较低;大流量时采用高扬程离心泵驱动,流量周期性波动不明显。本文提出的摇摆对单相流量波动产生明显影响的判据可合理解释不同文献中流量波动特性的差异。
4 结论
1)建立了摇摆条件下单相强迫循环流量波动分析模型,结果表明当驱动压头大于附加压降幅值的10~11倍时,摇摆条件下相对流量波动幅值小于5%,可近似认为摇摆对流动特性的影响可忽略。
2)增加回路阻力和驱动压头均能导致相对流量波动幅值迅速减小,实验结果和泵特性曲线结合回路阻力特性曲线的分析结果有很好的一致性。
3)初始流量恒定时,增加摇摆振幅和减小摇摆周期,即增加附加压降幅值使得相对流量波动幅值增大。
4)采用调节离心泵转速和调节阀门开度相结合的方式探索摇摆运动对单相流动产生明显影响的判据。实验结果和流量波动分析模型有很好的一致性。
[1]ZHANG J H,YAN C Q,GAO P Z.Characteristics of pressure drop and correlation of friction factors for single-phase flow in rolling horizontal pipe[J].Journal of Hydrodynamics:Ser,B,2009,21(5):614-621.
[2]曹夏昕,阎昌琪,孙立成,等.摇摆状态下竖直管内单相水摩擦压降特性分析[J].哈尔滨工程大学学报,2006,27(6):834-838.CAO Xiaxin,YAN Changqi,SUN Licheng,et al.Analysis of pressure drop characteristics of single-phase flowing through vertical rolling pipes[J].Journal of Harbin Engineering University,2006,27(6):834-838.
[3]刘晓钟,黄彦平,马建,等.摇摆条件下矩形窄缝通道单相等温流动摩擦阻力特性研究[J].核动力工程,2012,33(S1):54-58.LIU Xiaozhong,HUANG Yanping,MA Jian,et al.Frictional resistance characteristics of single-phase flow in narrow rectangular channel with rolling motion[J].Nucl Power Eng,2012,33(S1):54-58.
[4]TAN S,SU G,GAO P.Experimental and theoretical study on single-phase natural circulation flow and heat transfer under rolling motion condition[J].Applied Thermal Engineering,2009,29(14/15):3160-3168.
[5]刘培邦.摇摆状态下阻力特性分析[D].哈尔滨:哈尔滨工程大学,2008:31-45.LIU Peibang.Study on flow resistance characteristics under rolling[D].Harbin:Harbin Engineering University,2008:31-45.
[6]幸奠川,阎昌琪,曹夏昕,等.摇摆条件下单相水强制循环阻力特性实验研究[J].原子能科学技术,2011,45(6):672-676.XING Dianchuan,YAN Changqi,CAO Xiaxin,et al.Experimental study on forced circulation resistance characteristics of single-phase water flow under rolling condition[J].Atomic Energy Science and Technology,2011,45(6):672-676.
[7]XING D,YAN C,SUN L,et al.Effects of rolling on characteristics of single-phase water flow in narrow rectangular ducts[J].Nuclear Engineering and Design,2012,247:221-229.
[8]XING D,YAN C,SUN L,et al.Effect of rolling motion on single-phase laminar flow resistance of forced circulation with different pump head[J].Ann Nucl Energy,2013,54:141-148.
[9]王畅,高璞珍,谭思超,等.摇摆条件下强迫循环流量脉动特性分析[J].核动力工程,2012,33(3):56-60.WANG Chang,GAO Puzhen,TAN Sichao,et al.Analysis on Characteristic of forced circulation flow rate pulsation under rolling condition[J].Nuclear Power Engineering,2012,33(3):56-60.
[10]高璞珍,庞凤阁,王兆祥.核动力装置一回路冷却剂受海洋条件影响的数学模型[J].哈尔滨工程大学学报,1997,18(1):24-27.GAO Puzhen,PANG Fengge,WANG Zhaoxiang.Mathematical model of primary coolant in nuclear power plant influenced by ocean condition[J].Journal of Harbin Engineering University,1997,18(1):24-27.
Influence mechanism of rolling on the characteristics of flow fluctuation for single-phase forced circulation
XING Dianchuan,YAN Changqi,SUN Licheng
(National Defense Key Subject Laboratory for Nuclear Safety and Simulation Technology,Harbin Engineering University,Harbin 150001,China)
With a focus on the transient properties of the flow of single-phase forced circulation under rolling conditions,a study of the mechanism of the effects of flow fluctuation was carried out.The influences of the pressure head,flow resistance and additional pressure drop were analyzed by regulating the rotation speed of the centrifugal pump,state of the valve and rolling parameters respectively.And the mechanism of the effects of the rolling motion was revealed systematically by setting up the single-phase flow fluctuation equation.The results indicate that the fluctuation amplitude of the relative flow rate in rolling motion decreases rapidly as the pressure head and the flow resistance of the entire loop increase,and increase as the amplitude of the additional pressure drop increases.When the pressure head is higher than 10 to 11 times the amplitude of the additional pressure drop,the effect of the rolling motion on single-phase flow fluctuation could be neglected.The analysis result of the flow fluctuation equation is quite consistent with the results of the flow fluctuation experiments.
rolling motion;forced circulation;flow fluctuation;pressure head;theoretical model;Influence mechanism
10.3969/j.issn.1006-7043.201306020
http://www.cnki.net/kcms/doi/10.3969/j.issn.1006-7043.201306020.html
TL334
A
1006-7043(2014)06-0784-05
2013-06-04.网络出版时间:2014-05-14 15:51:27.
国家自然科学基金资助项目(11175050;51376052).
幸奠川(1986-),男,博士研究生阎昌琪(1955-),男,教授,博士生导师.
阎昌琪,E-mail:changqi_yan@163.com.

