基于弹性基础梁理论的球壳承压能力分析
熊志鑫,罗培林
(1.上海海事大学海洋科学与工程学院,上海201306;2.哈尔滨工程大学船舶工程学院,黑龙江哈尔滨,150001)
基于弹性基础梁理论的球壳承压能力分析
熊志鑫1,罗培林2
(1.上海海事大学海洋科学与工程学院,上海201306;2.哈尔滨工程大学船舶工程学院,黑龙江哈尔滨,150001)
为解决球壳的承压能力问题,从平板大挠度方程出发,假设板发生对称的球冠式初始弯曲变形,就能得出承受静水压力的球冠平衡方程,此方程可以简化成受横向载荷和轴向压力作用的弹性基础梁的平衡方程。通过弹性基础梁的屈曲问题,建立了球壳弹塑性失稳的极限强度和压杆临界应力的关系。在研究材料拉伸曲线的基础上,可以改进切线模量理论的计算方法,得出更简便、规范的切线模量因子算法。通过与大量深潜器球壳失稳的实验数据和数值数据比较,表明基于弹性基础梁理论的算法具有较高的准确性,可以推广用于计算承受均匀外压球壳的极限荷载。
大挠度;弹性基础梁;球壳;弹塑性;切线模量;承压能力
随着开发海洋的战略需要和深海勘探技术的不断发展,增大极限潜深是现代潜水器发展的一个主要方向。对于潜水器耐压结构,不仅要求其能承受较大的深水压力,同时还要求具有较小的重量。球形耐压壳在均匀外压力具有应力分布比较均匀、材料强度得到充分利用的优点,可以获得重量较轻承载能力较大的收益,因此成为深潜器最理想的结构形式,在深海工程中成为首选结构。弹性基础梁作为一种通用结构,其结构强度是工程人员比较熟悉的问题,曾在潜艇耐压圆柱壳的结构设计中得到深入应用[1]。近年来,被逐渐应用到球面舱壁及圆环壳结构中的强度分析[2-4]。这些应用说明,其可以解决许多旋转壳结构的工程实际问题。为此,本文从平板的卡门大变形方程出发,描述球壳的弯曲变形,并将球壳的弯曲问题转化为弹性基础梁的弯曲问题求解。
1 球壳对称弯曲的微分方程
假定球壳外表面受均压p作用,球壳在失稳前的变形是对称的,即认为有圆形固定边界的球冠变形对称于球冠的顶点,这可以通过设置坐标系的原点得到。已有试验结果表明[5],这种假设也能较准确地预报其破坏压力。如图1所示,u,v,w分别表示经线方向,纬线方向和径向方向的3个位移量。
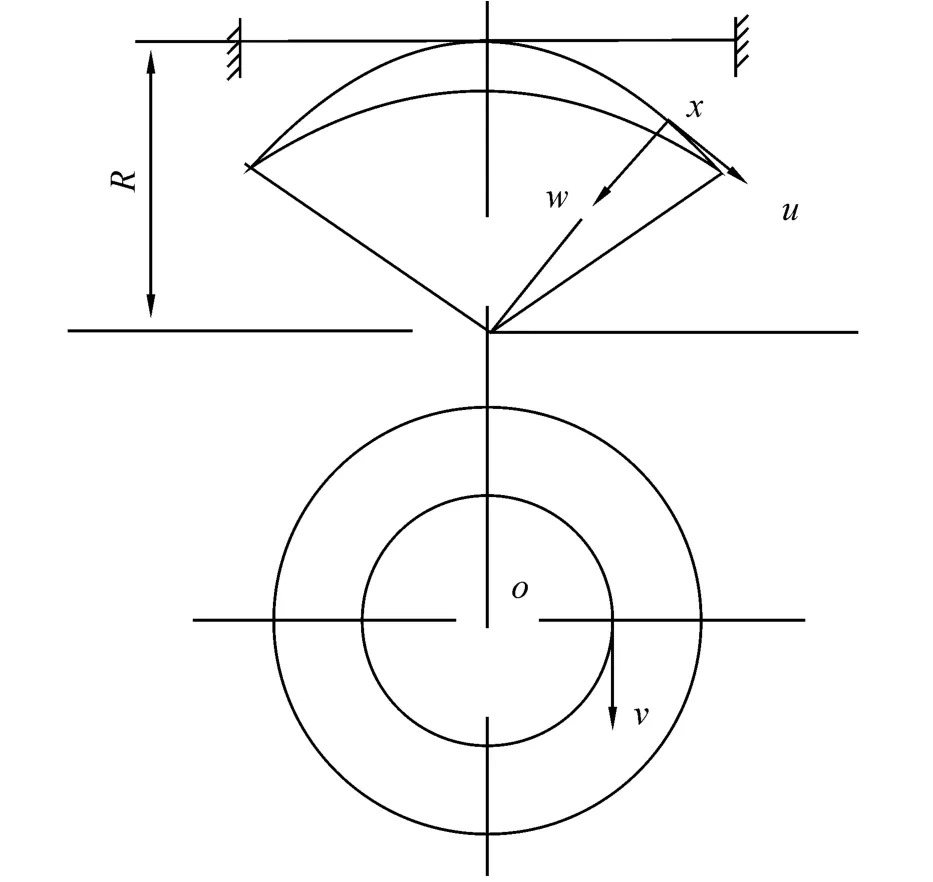
图1 平板的球冠式变形Fig.1 Deformation of a plate with deflection in form of a spherical cap
由于变形的对称性,可以判断它们都是坐标x的函数,而且v=0,则应力分量仅与位移分量u和w有关,并且也是坐标x的函数。将球冠看作是有初始球形初挠度的平板,即满足

式中:w0表示初挠度值,x、y分别表示平板2个方向坐标值。
下面从平板大挠度弯曲的基本微分方程出发,描述具有球冠形初挠度的平板弯曲情况。
理想平板大挠度弯曲的基本微分方程可以表示为

平衡方程:
式中:w为位移函数(挠度),φ为应力函数,t是平板厚度。在给定的边界条件下,解以上微分方程组求得w和φ,从而求出板的薄膜力和弯曲内力:

若平板产生如式(1)表示的初挠度,则

如图1所示,则平板的实际位移为w+we,代入式(2)得

具有初始曲率的平板,在压力p作用下变形时,它的应变分量是:

根据以上3个应变函数和虎克定律,可以得到初始变形为w0的平板的连续方程为
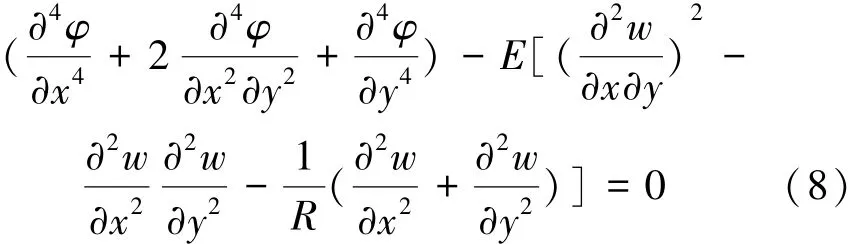
式(6)和(8)为扁球壳理论中球壳方程的相同表达形式,其中x、y代表球冠表面的径向和周向,如图1所示。令球冠的顶点为x轴的起点,则位移分量v=0,u,w仅为坐标x的函数。并且:

则胡克定律表示为
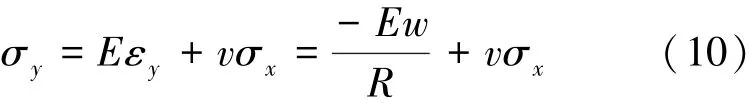
连续方程式(8)简化为

由于应力关于坐标原点x=0的对称性,式(12)可以直接从式(11)积分得到

式中:n1为应力系数,是积分常量。通过边界条件,可以确定n1的值,令x=0处的位移w为wx=0表示球冠顶点的位移,由于该点处经线和纬线2个方向的应力相等,即

根据式(10)、(12)、(13)可以得到表达式:

根据球冠弯曲变形的特点,式(6)可以简化为

式中:

式(15)即为弹性基础梁的平衡状态方程,从此式可以看出球冠的弯曲变形可以用板来描述,由于变形的轴对称性,板变形挠度w在y方向上没有变化,板处于筒形弯曲状态。筒形板的复杂弯曲状态求解就要用到复杂弯曲梁的结果,所以可以用弹性基础梁的计算方法应用到球壳强度的求解问题。
2 球壳失稳强度的弹性基础梁法
2.1 切线模量理论的改进表达
基于上述的理论分析,受压球壳的极限强度稳定可以归结为求解弹性基础梁的非线性失稳问题;弹性基础梁的临界应力又可以转化为梁杆的失稳问题求解。所以,球壳,弹性基础梁和梁杆的临界载荷求解方法一致,只是三者的结构刚度不同。通过无量纲的应力可以解决这一问题,并回归到材料的应力应变曲线;由求取的临界应力,再得出各自结构的临界载荷。在梁杆的临界应力求解中,按切线模量理论求得的临界力是最接近于压杆所能承受的最大荷载。所以,应用该理论方法求得的球壳承载能力也是较为接近实验结果的,并在深潜器耐压球壳的极限强度上得到广泛的应用[6]。
由于柱子曲线需要查表,且需通过测得每点的切线模量值形成图表计算。引入参数切线模量因子Φ,可以较好的将切线模量的表达显化,从而改进切线模量理论,得到更简便更规范的求解方法:

式中:ϕ=σ0/σE是代表欧拉应力或理想结构的参数,σ0为材料屈服应力或其他特定值。
n是表示结构缺陷的参数,称为协调因子,Φ为二者的乘积,即是表示实际承压结构的特征值。
设实际结构极限应力为σmax,理想结构的临界应力为σcr,则对于结构在非线性阶段失效的参数n可表示为

联合式(20)、(21),Φ可以表示为

由以上分析可知,切线模量因子Φ是耦合了结构特征和材料曲线的参数。
对于每一个极限平衡状态的应力,都有其对应的切线模量因子值Φ。所以,通过材料的应力应变曲线,可以得到表达平衡状态的σ--Φ曲线(n=1)。船舶与海洋常用材料的σ--Φ曲线如图2所示。σ--Φ曲线可以采用以下四参数方程表达[7]:

式中:A,B,c,m是表征材料的参数值。

图2 船用材料的切线模量因子曲线图Fig.2 Tangent modulus factor curves of marine material
观察图2所示的材料切线模量因子曲线特征,可以对σ--Φ曲线采用更为简便的直线式或二次式的表达:

将弹塑性失稳关于长细比λ的表达式代入式(23)得到


式中:
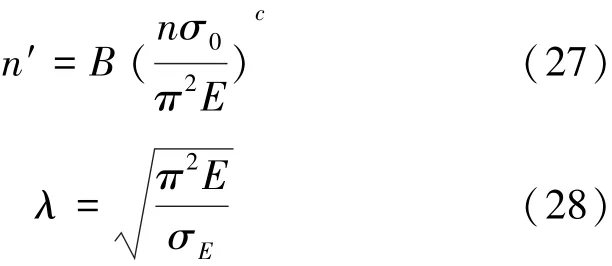
显然,通过取不同的表征材料的参数可得式(23)是包含柱子曲线一次表达式和二次算式的通式。
通过代入结构的欧拉应力至式(20),再输入结构对应的n值即可得到该结构的切线模量因子值,在分析材料拉伸曲线的基础上,将切线模量因子值代入到式(23)即得到承压结构的极限应力。
2.2 深潜球壳极限强度的计算与比较
无论是我国的潜水器耐压壳或潜艇结构设计计算规则,还是国外的泰勒水池海军公式,一般均是基于弹性稳定理论导出理论临界应力,再引入修正参数,分别计及初始挠度和材料非线性的影响,然后给出耐压壳实际失稳临界压力的计算公式。严格来说,壳体的几何非线性和物理非线性是交替影响的,但在处理上却机械地把它们割裂开来,在求解修正系数时没有同时考虑几何非线性和物理非线性的影响。通过引入n可以有效考虑这种影响,n既可以是单一的数值,也可以是ϕ的表达式,嵌入到物理非线性的表达中,使计算值更为准确。
2.2.1 钛合金深海球壳的极限承载力
1)钛合金的材料特性及表达。大深度潜水器耐压壳体的选材要求高比强度、高比刚度的金属或非金属,钛合金具有良好的机械性能,且重量轻、强度高,成为深潜器耐压壳的首选材料。该材料的σ-ε曲线和σ--ϕ曲线分别如图3和图4所示。
对于材料应力应变的非线性部分,可以采用下列拟合直线式来表达:
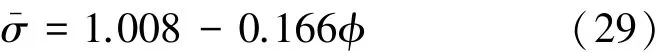
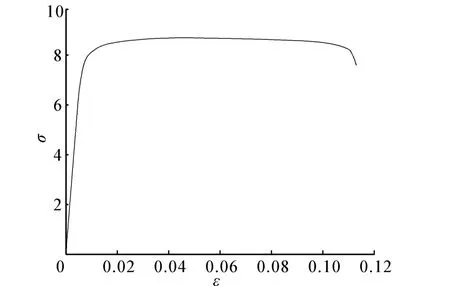
图3 钛合金的σ-ε曲线Fig.3 σ-ε curve of titanium alloy
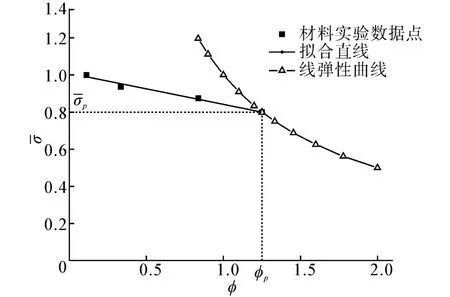
图4 钛合金的σ--ϕ曲线Fig.4 σ--ϕ curve of titanium alloy
2)钛合金深潜器球壳的简化表达式。在工程实际中,由于制作工艺因素,球壳总是存在初始挠度缺陷,残余应力等影响因素,这些因素将影响球壳的极限承载能力。这时可以引入综合因子n量化表示各种因素的影响。
实际极限状态下,式(29)可以表示为

根据球壳载荷和应力的对应关系,可方便求出对应的承压球壳极限载荷:

3)钛合金载人潜器球壳的结果分析。很多科研学者和研究机构对钛合金材料制成球壳的极限强度进行了多方面的深入研究和探索,可以将算式(30)的计算结果与数值及实验结果进行比较,如表1、2所示。

表1 式(29)与文献[8]数值计算结果的比较Table 1 Compare the FEM results of Ref.[8]with formula(29)

表2 式(29)与文献[6]实验值的比较。Table 2 Compare the experimental results of ref.[6]with formula(29)
由表1及图5可知,式(11)的计算结果与有限元方法的结果误差在10%以内。采用系数n表达由球壳制造工艺等产生的球壳初挠度对临界载荷进行修正,可以进一步减少误差值。

图5 式(29)计算值与有限元法结果的比较Fig.5 Comparison of formula(29)and FEM
2.2.2 TC4材料球壳的实验比较
1)TC4材料特性及切线模量因子表达式。TC4材料是“蛟龙”号设计阶段用于球壳实验模型的材料[9],其材料的σ--ϕ曲线如图6所示。根据实验数据,采用最小二乘法或数学软件拟合得到材料的切线模量因子表达式:
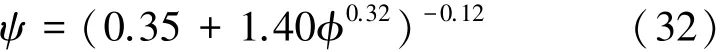

图6 TC4合金的σ--ϕ曲线Fig.6 σ--ϕ curve of TC4 alloy
2)TC4试验球壳。文献[9]对TC4合金材料制成的1#和2#球壳进行试验。2个球壳的参数如表3所示,其中2#球壳的不圆度达到1.812 4 mm,超过允许的250×0.5%=1.25 mm,所以,引入因子n对其进行修正。当取参数n=20以量化误差时,计算值与试验值的误差在5%范围内。

表3 与文献[9]模型实验结果的比较Table 3 Compare the results of experiment with Ref.[9]
2.3 开孔球壳的简化模型
根据前述的推导分析,球冠可以用弹性基础梁的力学模型表达,那么球台壳体部分也可以应用这一模型来说明。球台边界的封闭端,例如耐压壳开孔的观察窗等也可以使用弹性基础梁的力学模型。其力学简化模型如图7所示,两端部分是球台结构,中间长度l部分是开孔补强构件。

图7 开孔球壳的简化弹性基础梁计算图Fig.7 Simplified calculating model based on elastic foundation beam spherical hull with a hole
文献[10]对带大开口观察窗的球形耐压壳的非线性稳定性进行分析,耐压壳的参数如表4所示。球壳部分材料为16MnR,根据材料的拉伸曲线可得其σ--ϕ曲线的拟合表达式如式(33)所示,并进一步得出计算结果如表5所示。
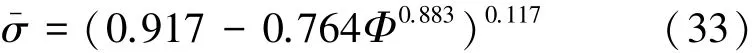

表4 耐压壳的结构和材料参数Table 4 Structure parameter and material parameter of pressure hull

表5 各种方法的分析结果比较Table 5 The results comparison among several methods with experiment results
由以上分析可知,由于观察窗的高强度,球壳的失稳强度仍然取决于球壳部分。显然,本文提供的方法比有限元分析值要低,这对于设计是偏安全的。本文提供算法较泰勒水池公式的方法更为准确,原因在于基于切线模量理论求得的临界力比双模量算法更接近于压杆所能承受的非弹性荷载。
3 结论
通过以上分析,得出承受外压球壳的等效弹性基础梁算法,并为开孔球壳的简化计算模型指明理论基础。通过本文的分析,还可以得出以下结论:
1)本文提供的切线模量因子算法表达规范,计算简便,计算结果准确且比试验值偏安全,值得在深潜器耐压球壳初步设计中推广使用;
2)协调因子n值是半解析半经验参数,可以在理论求解和试验数据的配合下完善其表达,以进一步提高计算精度;
3)选择合适的材料拉伸曲线表达式有助于简化计算,提高准确率;然而,当前合金材料的性能研究并未十分成熟,关于材料拉伸曲线的试验数据表达和评估仍然值得进一步的研究。
[1]徐秉汉,朱邦俊,欧阳吕伟,等.现代潜艇结构强度的理论与试验[M].北京:国防工业出版社,2007:45-67.
[2]蔡新钢,朱邦俊.球壳开孔应力分析的一种解析方法[J].船舶力学,2007,11(5):759-767.CAI Xinggang,ZHU Bangjun.An analytical method for stress of opening in spherical shell[J].Journal of Ship Mechanics,2007,11(5):759-767.
[3]朱邦俊,王丹,万正权.端部球面舱壁应力近似解[J].船舶力学,2011,15(11):1255-1263.ZHU Bangjun,WANG Dan,WAN Zhengquan.An analytical solution for stress of the end spherical bulkhead[J].Journal of Ship Mechanics,2011,15(11):1255-1263.
[4]邹广,彭兴宁,杜青海.加筋圆环壳的理论求解及性能研究[J].船舶力学,2012,16(1-2):83-92.ZOU Guang,PENG Xingning,DU Qinghai.Theoretical solution and essential research of the ring-stiffened toroidal shell[J].Journal of Ship Mechanics,2012,16(1/2):83-92.
[5]郑衍双,陆正福,张定武.均匀外压下有几何缺陷球壳的破坏压力[J].中国造船,1986,162(1):48-58.ZHENG Yanshuang,LU Zhengfu,ZHANG Dingwu.Collapse pressure of spherical shells with initial imperfections under uniform pressure[J].Shipbuliding of China,1986,162(1):48-58
[6]刘涛.深海载人潜水器耐压球壳设计特性分析[J].船舶力学,2007,11(2):218-219.LIU Tao.Research on the design of spherical pressure hull in manned deep-sea submersible[J].Journal of Ship Mechanics,2007,11(2):214-220.
[7]熊志鑫,张志平,佟福山.材料衍生比例定律的建立及其在结构屈曲断裂非线性失效中的应用[J].船舶力学,2011,15(4):377-382.XIONG Zhixin,ZHANG Zhiping,TONG Fushan.Estabilishment of derivative proportional law and its application in elastic-plastic buckling and fracture of structures[J].Journal of Ship Mechanics,2011,15(4):377-382
[8]PAN Binbin,CUI Weicheng.An overview of buckling and ultimate strength of spherical pressure hull under external pressure[J].Marine Structures,2010(23):227-240.
[9]PAN Binbin,CUI Weicheng,SHEN Yunsheng.Experimental verification of the new ultimate strength equation of spherical pressure hulls[J].Marine Structures,2012(5):1-8.
[10]卢骏锋,赵耀,张维衡.带大开口观察窗的球形耐压壳的稳定性分析[J].中国造船,2008,184(1):135-141.LU Junfeng,ZHAO Yao,ZHANG Weiheng.The stability analysis of sphercial pressure shell with a large opening[J].Shipbuilding of China,2008,184(1):135-141
Analysis of the pressure-bearing capacity of spherical hulls using the elastic foundation beam theory
XIONG Zhixin1,LUO Peilin2
(1.College of Ocean Science and Engineering,Shanghai Maritime University,Shanghai 201306,China;2.College of Shipbuilding Engineering,Harbin Engineering University,Harbin 150001,China)
In order to analyze the pressure-bearing capacity of spherical shells,the equilibrium equation of a spherical cap subjected to hydrostatic pressure may be obtained on the basis of the plate large-deflection equation,assuming that a symmetrical spherical-cap type of initial bending deformation occurs on a plate.This equation can be simplified to the equilibrium equation of the elastic foundation beam subjected to the lateral and axial loads.Through the buckling of the elastic foundation beam,the relationship between the ultimate strength of the spherical hull at a loss of the elastic-plastic stability and the critical stress of a pressure bar can be established.Based on the stressstrain curve of the material,the method of the tangent modulus theory may be improved,and the improved algorithm is more simplified and standardized.When comparing the large number of experimental results with the calculation data,this method based on the elastic foundation beam theory proves to have a higher quality of accurateness,and this method can be applied to calculating the ultimate strength of spherical hulls under pressure.
large deflection;elastic foundation beam;spherical hull;elastoplasticity;tangent module;pressurebearing capacity
10.3969/j.issn.1006-7043.201304044
http://www.cnki.net/kcms/doi/10.3969/j.issn.1006-7043.201304044.html
TU344.3
A
1006-7043(2014)06-0690-06
2013-04-11.网络出版时间:2014-05-14 15:53:42.
国家自然科学基金资助项目(51108259);上海高校选拔培养优秀青年教师专项基金资助项目(shhs12056);2013年上海市研究生教育创新计划实施项目(20131129).
熊志鑫(1983-),男,讲师,博士;罗培林(1928-),男,教授,博士生导师.
熊志鑫,E-mail:zxxiong@shmtu.edu.cn.

