GPU在SPH方法模拟溃坝问题的应用研究
杨志国,黄兴,郑兴,段文洋
(哈尔滨工程大学船舶工程学院,黑龙江哈尔滨150001)
GPU在SPH方法模拟溃坝问题的应用研究
杨志国,黄兴,郑兴,段文洋
(哈尔滨工程大学船舶工程学院,黑龙江哈尔滨150001)
SPH方法是一种无网格的粒子方法,对于求解强非线性水动力学问题具有重要意义。随着粒子数增加,该方法的计算效率成为限制其大规模工程应用的重大瓶颈。可将大规模并行计算引入SPH方法中,以得到良好的计算加速效果。采用将GPU运用于SPH方法并行计算的技术,借助CUDA硬件计算架构,研究SPH方法的并行计算通用性问题。以二维溃坝问题作为数值算例,对GPU计算结果的稳定性和收敛性进行验证,比较CPU与GPU的计算效率。通过计算,验证了GPU在SPH方法并行计算应用中的可靠性、可行性以及高效性,为提高SPH方法的计算效率提供一种重要的参考途径。
GPU;并行计算;CUDA;SPH方法;溃坝;水动力学;数值计算;
SPH方法是一种基于拉格朗日力学的无网格粒子法,该方法通过将连续的流场离散成一系列的流体粒子,而后用离散的流体粒子通过核近似的方式代替连续流场,并求解离散后的流场动力学方程。由于SPH方法的无网格特性以及带有相应物理量的粒子的自由运动的特点,使得SPH方法在研究带有强非线性自由表面的流场问题等领域中有着独特的优势。SPH方法最早是在求解天体物理问题[1-2]时提出,后经一系列研究发展,其研究领域得到不断拓展,如应用于可压缩非耗散流体问题[3]、弹性和断裂问题[4]、弱可压缩流体自由表面流动问题[5]、波浪破碎问题[6-7]。
随着计算机科学的不断发展以及科学计算中对计算机的性能要求不断提高,图形处理器(graphics processing unit,GPU)作为新型的计算处理单元,以其强大的并行计算能力,满足了诸多领域的计算需求,近年来得到迅猛的发展。其功能已由最初的图形处理加速的简单需求,转变为新型的面向计算机通用计算平台的通用计算图形处理器(general purpose GPU,GPGPU)。目前,GPU在物理[8]、生物[9]、化学[10]等诸多科学领域已经得到较为广泛的应用。
针对SPH方法计算过程中的效率问题,将GPU应用于SPH方法计算中,是提高计算实效的有效途径。目前,SPH的GPU并行研究主要集中于流体实时模拟问题[11]、近海海浪仿真[12]等问题。
由于GPU平台下SPH方法并行计算结果可靠性问题研究目前尚不充分,本文首先介绍了基于GPU平台的SPH并行计算方法,之后着重对GPU模拟二维溃坝问题数值结果的收敛性与稳定性进行详细研究,探讨GPU并行架构在SPH方法求解溃坝问题中的可行性。之后,根据GPU硬件特性和数值求解结果,对CPU-GPU计算效率以及GPU内线程数量对计算效率的影响进行重点分析,从而为GPU上实现SPH方法并行计算,验证求解结果可靠性,提高SPH方法计算效率等问题提供一定参考。
1 SPH方法

式中:Ω为包含x的积分体积,f为三维坐标向量x的函数;δ( x-x′,h )为δ函数,性质如下:
在SPH方法中f x()函数的积分表达式定义为

经离散化后N-S方程质量守恒,动量守恒的SPH表达式可写为

本文选取Monaghan[13]提出的三次样条函数作为核函数。边界粒子布置采用镜像法[14],镜像粒子满足方向不可穿透,镜像可滑移条件。此外,为确保数值结果的稳定性,传统的弱可压缩SPH方法需考虑人工压缩性、人工粘性[5]等问题,对于人工粘性问题,特别是对粘性系数选取问题,许多学者进行了深入研究[15]。
2 CUDA架构
GPU一般存在于计算机的显卡中,拥有多处理器结构。随着计算机科学的不断发展,GPU已经从原本的图形处理器逐步转变为适合处理具有较高计算密度和简单逻辑分支任务的通用处理器。
目前,市场上出售的GPU主要是NVIDIA和AMD/ATI两家公司的产品。本文适用NVIDIA公司GTX660产品。
2.1 CUDA及存储模型
统一计算设备架构(compute unified device architecture,CUDA)是NVIDIA公司于2007年6月推出的计算架构体系,它为GPU应用于数据并行计算提供了一套完备的硬件架构和软件体系。CUDA编程模型中,分为主机(Host)与设备(Device)或者主机(Host)与协处理器(co-processor)[16]。主机是CPU在CUDA中的代号,而设备、协处理器则是GPU的代号,之所以将二者分开来,主要是为了便于在调用CPU或GPU时区分两者功能。GPU上每个完整的处理核心称为一个core。
设备端内存种类较多,以其在执行过程中作用不同,可分为全局存储器、常数存储器、纹理存储器、局部存储器、共享寄存器和寄存器[16]。
2.2 执行方式及执行单位
CUDA执行以主机端控制设备端,设备端返回给主机端的执行结果的方式进行。当执行任务时,先由主机端程序开辟任务所需的内存或显存,然后将主机端数据拷入显存中,设备端接收到主机端的执行指令后执行相应的任务要求,执行结束后,将执行结果传递给主机端,主机端释放开辟的内存或显存,执行结束,执行过程如图1所示。

图1 GPU-CPU执行模式Fig.1 GPU-CPU execution model
CUDA线程是设备端运行的基本单位。线程是以Grid、Block、Thread为层次机构执行的。每个Block由若干个Thread组成一维、二维或者三维形式,而每个Grid则由若干个Block组成一维、二维或者三维形式。在设备端执行的过程中,线程作为最小执行形式被分派到Block中,而Block又被分派到Grid中,控制器将Block发送到流多处理器中,进而将线程发送到流处理器中计算相应指令,执行结束后完成设备端计算任务,返回主机端。
2.3 SPH并行模式
本文在SPH方法的每步迭代过程中,以单线程控制单个流场粒子,以多线程同时执行的方式计算不同粒子的相应流场物理量。线程数量的多少取决于GPU硬件的配置,而并行效率则与线程数量和GPU计算能力有很大的关系。
初始时刻,先将粒子信息考入显存当中,在GPU上完成所有计算任务,之后将所得结果返回CPU,减少了由于CPU-GPU数据通讯花费的计算时间。每步计算过程中,采用链表查找法对所有粒子进行排序,采用改进欧拉迭代法,具体流程如图2所示。
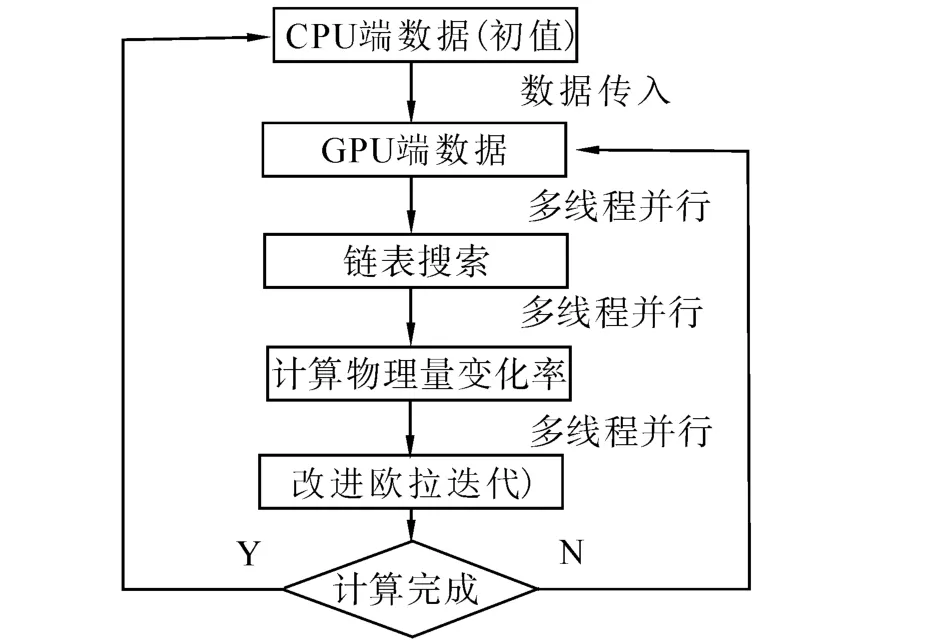
图2 SPH并行方式Fig.2 SPH parallel manner
3 二维溃坝模拟
本节以二维溃坝问题为研究对象,验证GPU并行方法的可靠性与实用性问题。计算平台为Intel i5-3570 CPU,8 G内存,GTX660显卡。
3.1 溃坝模型
溃坝模型如图3所示。
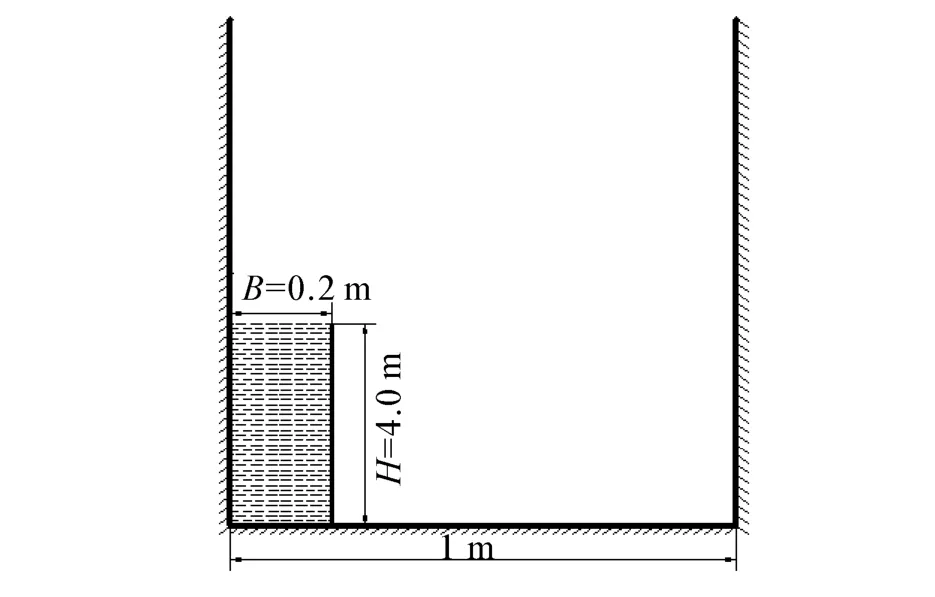
图3 溃坝模型Fig.3 Dam breaking model
水柱宽度B=0.2 m,高度H=0.4 m。矩形体宽度为1 m,光滑长度h=0.01 m,粒子总数为800,初始时刻粒子间距与光滑长度相等。ρ0=1 000 kg/ m3,采用弱可压缩性假设,时间步长取0.1 ms。
3.2 计算结果及分析
图4给出了T为0.1、0.4、0.7、0.9、1.05 s的SPH方法的GPU计算结果。计算结果较好地描述了从溃坝开始,溃坝前端触壁、爬升、翻卷,二次入水等强非线性特征的典型模拟过程。

图4 不同时刻计算结果(800粒子)Fig.4 Calculation result at different time(800 particles)
比较水柱前缘位置是验证计算结果准确性的重要参考。取时间步长为0.1 ms,将计算结果与Martin[17]等的实验结果、Lee[18]等的VOF方法、徐卜男[19]SPH方法的数值结果进行比较,如图5所示。本文计算值与Lee、徐等数值模拟结果吻合较好,但与实验值相比,数值结果普遍呈现出偏快的特点。

图5 水柱前缘位置比较Fig.5 Comparison of water column front edge position
3.3 收敛性分析
收敛性分析作为验证数值结构的有效性与可靠性的重要手段,一直都作为研究论证的重点。本文采取相同粒子数量下不同时间步长以及相同时间步长下不同的粒子数量2种方式验证收敛性。
3.3.1 时间步长影响
考察相同粒子数下不同时间步长的影响,本文以粒子数为800时为例,时间步长分别取为0.1、0.05、0.01、0.005 ms。
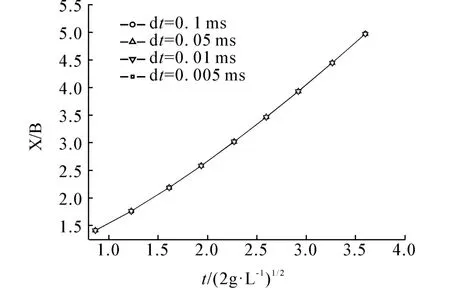
图6 不同时间步长比较Fig.6 Comparison of different time steps
图6 表明,水柱前缘随着计算时间步长的改变,变化并不显著,结果表明数值计算结果趋于稳定,GPU并行计算取得良好的收敛性。
3.3.2 粒子数目对溃坝问题的影响
研究流场中粒子数量多少对数值结果的影响,是收敛性分析的重要工作之一。本小结保持计算域的大小不变,时间步长取为0.01 ms,光滑长度为0.01、0.005、0.004、0.002和0.001 m所对应的粒子数分别为N=20×40、N=40×80、N=50×100、N=100×200、N=200×400。
图7分别取T=0.3 s、T=0.6 s、T=1.0 s、T=1.1 s 4个时刻自由液面数值结果。结果表明,在溃坝开始的最初阶段,粒子数的数值结果自由表面形状吻合较好,至前缘爬升阶段仍较为一致。出现翻卷时,自由表面开始显现出差异,尤其是水舌前部重新入水以及出水后的形状有些许差异。但这种差异随着粒子数增加而减小,计算结果趋于稳定。
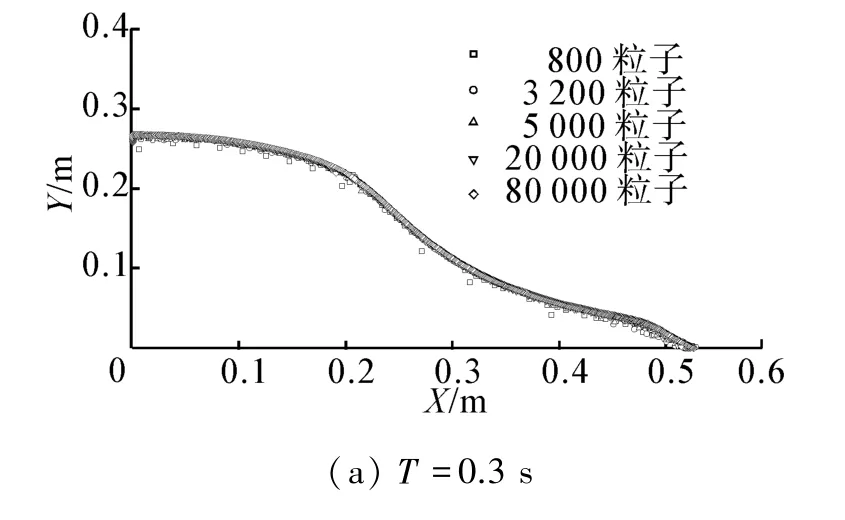
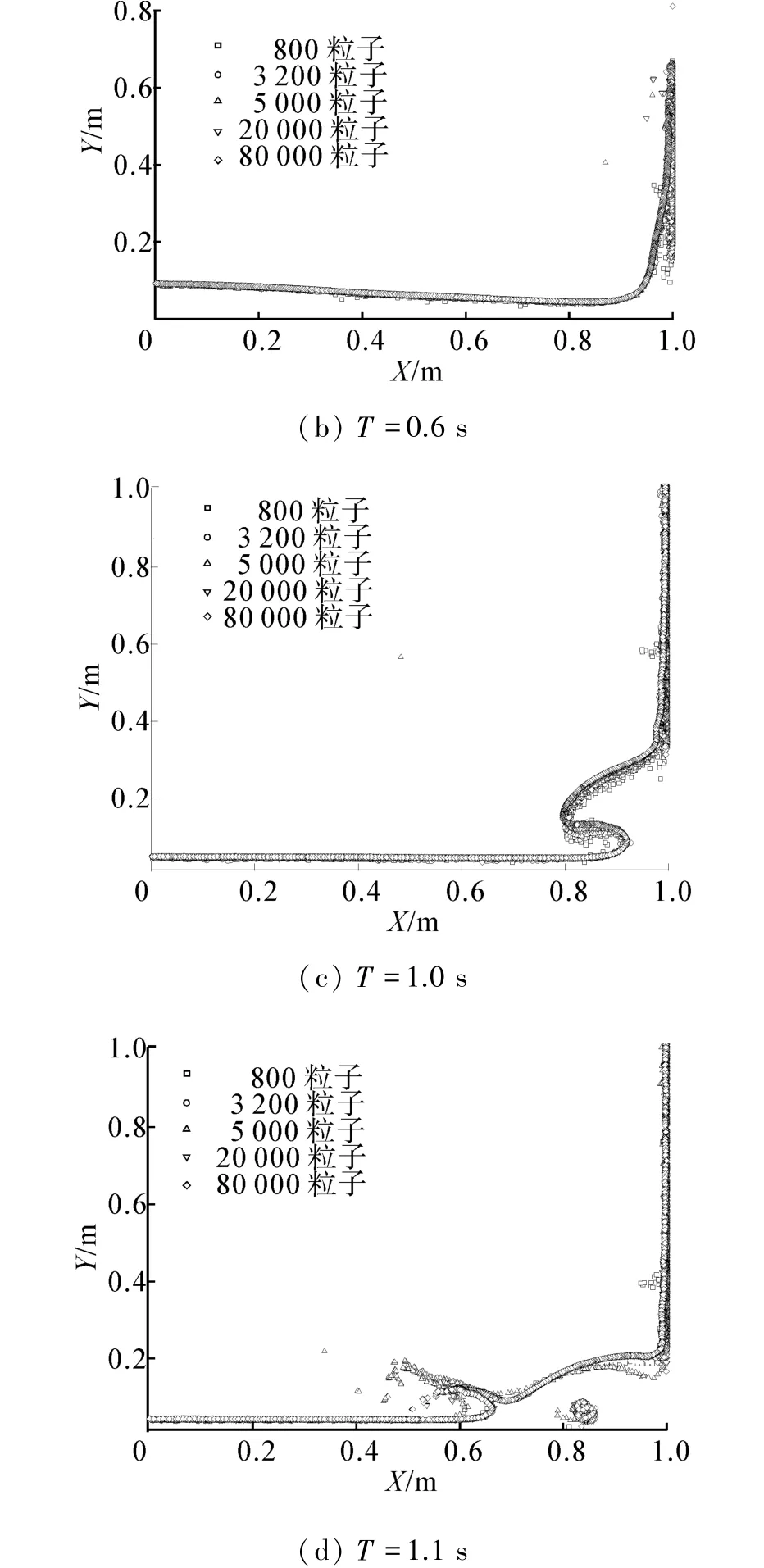
图7 自由液面不同粒子数比较Fig.7 Free surface comparison of different particle number
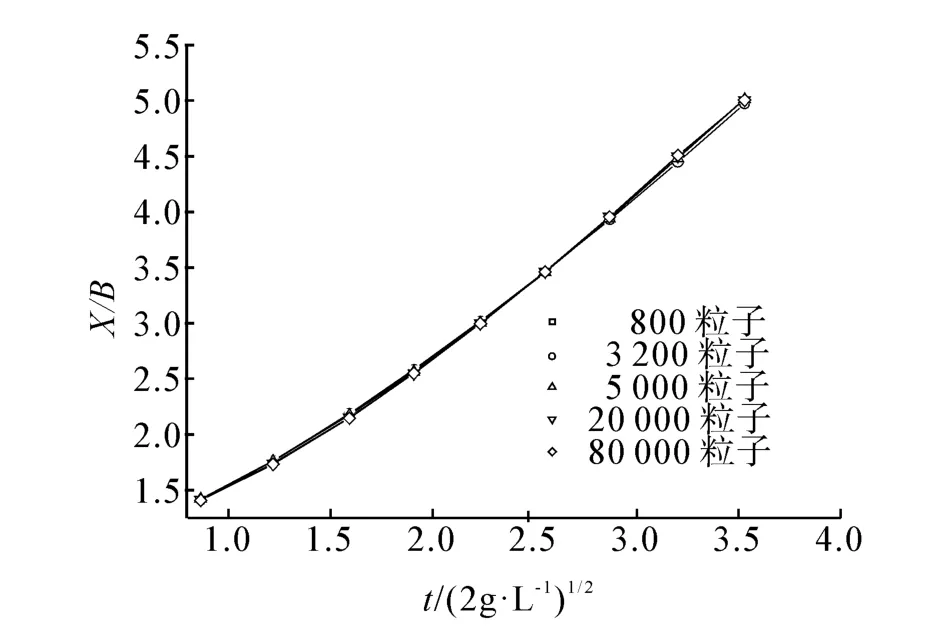
图8 不同粒子数水柱前缘对比Fig.8 Front edge contrast of different particle number
从图8中可以看出,当粒子数增加时,水柱前缘位置呈先慢后快的趋势,但差距不超过1%。
3.4 计算时间
文章通过将GPU计算耗时长度与CPU计算耗时进行对比,研究GPU的加速效率问题。GTX660显卡拥有960 core,2G显存,GPU主频频率为1 033 MHz,每个线程块中理论上允许同时使用的最大线程数量为1 024。CPU采用i5 3570型号,主频为3.4 GHz。本节取粒子数分别为800、3 200、5 000、20 000、80 000,时间步长取0.01 ms,计算150 000步。分析GPU线程对计算速度的影响以及比较CPU-GPU间计算效率问题。
3.4.1 GPU线程影响
本小节分别取单个Block内线程数量为128、256、512、768,比较分析不同线程数量对计算效率的影响。图9显示了粒子数相同情况下,取不同线程所需的平均单步计算时间,从图中可以看出,GPU的计算效率并不是随着线程数量的增加而呈现出简单的递增关系,线程数量越多,计算时间未必越少,在本算例中单块内的线程数取256时,不同粒子数下计算时间均为最短,而当线程数增加或减小时,计算所需时间反而增加,且粒子数不同,增加的趋势也不尽相同。

图9 线程时间比较Fig.9 Time comparison of thread spend
3.4.2 CPU-GPU比较
分析比较CPU与GPU计算时间的差异,是本文工作的重点之一。图10显示了2种不同计算核心的计算时间对比。
当粒子数量为800时,CPU运算速度较GPU有14%的增速,其原因在于GPU的单线程计算能力不及CPU,在计算量相对较小的情况下,CPU在计算时间上显现出一定的优势。但随着粒子数的逐渐增加,GPU多线程优势开始发挥,从2.35倍的加速效果递增至3.89倍,同时,随着粒子数的增加,GPU并行计算加速效果更加明显。

图10 CPU-GPU时间比较Fig.10 Time comparison of CPU and GPU
4 结论
本文以GPU为计算平台,研究SPH方法溃坝问题并行计算的数值模拟方法,结果表明:
1)GPU用于SPH方法并行计算研究的可靠性。本文以SPH方法理论和GPU计算结果为依据,将数值结果与实验值比较,通过取不同粒子数以及不同时间步长进行收敛性验证,表明GPU并行计算求解水动力学问题的可靠性与适用性。
2)GPU并行加速SPH方法的有效性。比较GPU与CPU计算时间,单步GPU的计算加速最高时达到CPU计算时间的3.89倍,随着计算量的增加,加速效果逐渐凸显,由此可见,GPU在研究SPH方法并行计算中存在很大的适用性。
3)在SPH方法计算过程中,GPU线程数量对计算时间影响较大。通过相同粒子数下不同线程数量对计算时间比较可知,线程数量对计算速度而言有显著影响,但并不成正比关系。使用GPU时,综合考虑硬件特点以及研究问题的特殊性,结合合理的算法,是取得良好加速效果的重要保证。
[1]GINGOLD R A,MONAGHAN J J.Smoothed particle hydrodynamics:theory and application to non-spherical stars mon[J].Monthly Notices of the Royal Astronomical Society,1977,181:375-389.
[2]LUCY L B.A numerical approach to the testing of the fission hypothesis[J].Astronomical Journal,1977,82:1013-1024.
[3]LIBERSKY L,PETSCHEK A G.Smooth particle hydrodynamics with strength of materials advances in free Lagrange methods[J].Lecture Notes in Physics,1991,395:248-257.
[4]GINGOLD R A,MONAGHAN J J.Kernel estimates as a basis for general particle methods in hydrodynamics[J].Jour-nal of Computational Physics,1982,46:429-453.
[5]MONAGHAN J J.Simulating free surface flows with SPH[J].Computational Physics,1994,110:399-406.
[6]MONAGHAN J J.Energy distribution in a particle alpha model[J].Journal of Turbulence,2004,5:22.
[7]郑兴,马庆位,段文洋.K2_SPH方法及二维破碎波的模拟[J].计算物理,2012,29(3):317-325.ZHENG Xing,MA Qingwei,DUAN Wenyang.K2_SPH method and simulation of 2D breaking waves[J].Journal of Computational Physics,2012,29(3):317-325.
[8]JIA X,PAGANETTI H S J,JIANG S B.GPU-based fast Monte Carlo does calculation for proton therapy[J].Physics in Medicine and Biology,2012,57(23):7783-7797.
[9]JONES E A,Van ZEIJL R J M,ANDREN P E,et al.High speed data processing for imaging MS-based molecular histology using graphical processing units[J].Journal of the A-merican Society for Mass Spectrometry,2012,23(4):745-752.
[10]CHENG Ling,BENKRID K.Design and implementation of a CUDA-Compatible GPU-based core for gapped BLAST algorithm[J].Procedia Computer Science,2010,1(1):495-504.
[11]郭秋雷,唐逸之,刘诗秋,等.一个SPH流体实时模拟的全GPU实现框架[J].计算机应用与软件,2011,28(11):69-72.GUO Qiulei,TANG Yizhi,LIU Shiqiu,et al.A full GPU implementation framework of SPH fluid real-time simulation[J].Computer Applications and Software,2011,28(11):69-72.
[12]陈俊.近海海浪的仿真研究[D].武汉:武汉理工大学,2011:13-14.CHEN Jun.Research on simulation of waves in shallowwater[D].Wuhan:Wuhan University of Technology,2011:13-14.
[13]FLUCK D A,QUINN D W.An analysis of 1-D smoothed particle hydrodynamics Kernels[J].Journal of Computational Physics,1996,126:699-709.
[14]LIU G R,LIU M B.Smoothed particle hydrodynamics:a meshfree particle method[M].Singapore:World Scientific Publishing Co.Pte.Ltd,2003:138-141.
[15]ZHENG Xing,DUAN Wenyang.Numerical simulation of dam breaking using smoothed particle hydrodynamics and viscosity behavior[J].Journal of Marine Science,2010,9:34-41.
[16]张舒,褚艳利,赵开勇.GPU高性能运算之CUDA[M].北京:中国水利水电出版社,2009:14-16.
[17]MARTIN J C,MOYCE W J.An experimental study of the collapse of liquid columns on a rigid horizontal plane[J].Philosophical Transactions of the Royal Society of London A,1952,244(882):312-324.
[18]LEE B H,PARK J C,KIM M H,et al.Numerical simulation of impact loads using a particle method[J].Ocean Engineering,2010,37(2/3):164-173.
[19]徐卜男.SPH方法模拟液舱晃荡及量纲分析[D].大连:大连理工大学,2011:45-51.XU Pu′nan.SPH simulation and parametric analysis on sloshing tank[D].Dalian:Dalian University of Technology,2011:45-51.
The application research of GPU in the SPH method to simulate the dam breaking problem
YANG Zhiguo,HUANG Xing,ZHENG Xing,DUAN Wenyang
(School of Shipbuilding Engineering,Harbin Engineering University,Harbin 150001,China)
As a mesh-free particle method,the SPH method is very important for dealing with the hydrodynamic problems with strong nonlinear problems.However,following the increase of the particle number,the calculation efficiency becomes a bottleneck for applying the method to the engineering practice.Good acceleration performance can be attained by applying massively parallel computing into the SPH method.In order to study the general parallel purpose of the SPH method,the parallel technology through the use of GPU on the compute unified device architecture platform has been used.The convergence and the stability of the computing results generated by GPU have been verified and the computational efficiency of GPU and CPU has been compared according to the computing results by using a numerical example of the two-dimensional dam-breaking problem.The capability,feasibility and high efficiency of GPU computing have been proved by the results which provide important reference channels to increase the calculation efficiency of the SPH method.
graphics processing unit(GPU);parallel computing;compute unified device architecture(CUDA);SPH method;dam breaking;hydrodynamic;numerical simulation
10.3969/j.issn.1006-7043.201305062
http://www.cnki.net/kcms/doi/10.3969/j.issn.1006-7043.201305062.html
O352
A
1006-7043(2014)06-0661-06
2013-05-23.网络出版时间:2014-05-14 15:49:41.
国家自然科学基金资助项目(51009034,51279041).
杨志国(1964-),男,副研究员.
杨志国,E-mail:yangzhiguo@hrbeu.edu.cn.

