基于总体坐标法的大变形锚泊线的静力分析
马刚,孙丽萍
(哈尔滨工程大学船舶工程学院,黑龙江哈尔滨150001)
基于总体坐标法的大变形锚泊线的静力分析
马刚,孙丽萍
(哈尔滨工程大学船舶工程学院,黑龙江哈尔滨150001)
为解决锚泊线轴向大拉伸问题,提出了一种联合应用总体坐标、能量变分原理和有限元法的解决方法。通过总体坐标使用节点斜率取代转角,直接在总体坐标系下以当前构形形成微元非线性应变位移关系的描述方法,同时建立当前构形与参考构形下的参量映射关系;利用能量变分原理建立应变能和外力功的平衡方程,进而形成锚泊线的单元刚度矩阵;按照有限元法完成单元组装和数值求解。这种方法在三维空间内较为准确地刻画了锚泊线的大转动和大拉伸变形,并且在单元组装时,不必进行局部坐标与总体坐标之间的转换,节省了计算时间。与具有解析解的可拉伸悬链线理论的对比显示,该方法具有较快的收敛速度和较高的计算精度。
总体坐标;能量变分原理;有限元法;锚泊线;静力分析
锚链是深水浮式结构物进行锚泊定位的主要构件之一。在计算分析中,一般认为锚链完全柔性,不具备抗弯能力,属于锚泊线构件[1]。因为锚链由较高强度的钢材构成,在工作载荷下只有较小的应变产生,所以通过在经典悬链线理论中假设锚链没有轴向拉伸或小拉伸,也可以得到较为可靠的计算结果。在这种假设下,集中质量法和细长杆法也是对完全柔性的锚泊线进行分析的重要理论[2-3]。集中质量法采用能量原理和有限元法,通过单元局部坐标和总体坐标的转换完成总体刚度矩阵的组装;细长杆法在总体坐标系中使用矢量力学方法和有限元法,省去了单元局部坐标与总体坐标的转换,并且与集中质量法相比,基于总体坐标法的细长杆法不再使用转角作为单元坐标,而是使用斜率,这种方式具有更灵活的特性。基于总体坐标方法的索、杆、梁等单元的研究在海洋工程和其他学科中也得到了广泛的关注[4-8]。但是,目前对于索单元的研究限制在轴向无变形和小变形的假设下。一般认为悬链式锚链通过自身的重力效应产生较大的水平力从而实现定位功能。在精确度要求不高的工程应用中,假设缆索轴向无拉伸或小拉伸,虽然计算结果仍然较为可信,但却不符合实际情况,因为它忽略了轴向弹性变形对锚泊力的贡献,这在由聚酯材料构成的张紧式锚泊线中的体现尤为明显。在张紧式锚泊线中,水平锚泊力主要通过缆索的轴向弹性变形获得。这也要求对锚泊线的研究必须较为严格地考虑轴向变形因素。另外,由于小变形假设不区分变形前后的构形和采用了线性几何关系,因此不能直接应用于大变形的分析中。
总体坐标法的相关理论正在持续发展,并形成了矢量力学总体坐标法和能量变分总体坐标法。在海洋工程中,矢量力学总体坐标法已经有了较为深入的研究,不过,目前大多用于研究大弯曲变形和轴向小(无)拉伸变形。能量变分总体坐标法目前主要在机械、多体动力学等领域内应用,并集中在全参数实体杆梁单元的研究上[9],针对应用在深水环境中的锚链等一维柔性构件的研究还不深入[10]。在矢量力学总体坐标法中,单元坐标由15个分量构成,包括6个平动坐标,6个斜率坐标和3个拉格朗日乘子(近似张力)。通过能量变分总体坐标法形成的单元坐标由前12个分量构成,这在一定程度可以减少求解方程数量[11]。本文借助总体坐标法来研究锚泊线的轴向大变形问题。利用能量原理和有限元法提出一种解决轴向大变形问题的锚泊线静力计算方法。
1 锚泊线的能量变分总体坐标法
1.1 基本假定
在分析中,锚泊线的计算方法将遵循以下假设:1)刚性截面假设:截面在外载荷作用下截面尺寸和形状不发生变化,即由于锚泊线轴向尺寸远远大于截面尺寸,因此截面变形忽略不计。2)锚泊线发生变形后,中心线和截面依然保持垂直,且忽略相对扭转。3)材料线弹性假设:应力和应变呈线性关系。4)完全柔性假设:锚泊线不具备抗弯能力,完全依靠张力维持平衡。5)质量守恒:变形前后总质量不发生变化。
1.2 总体坐标法和非线性应变位移关系
深水锚泊线的轴向尺寸远远大于截面尺寸,因此将其中心线当做一条空间中的曲线来进行模拟。将无应力状态的曲线看作参考状态,曲线上任意一个质点可以由矢径r表示(即总体坐标),其中矢径是参考构形下弧长s的函数。曲线在外载荷的作用下,由参考状态转变为变形后状态(或称当前状态)。在变形后状态下,矢径r是变形后弧长s~的函数。在曲线任意质点上均伴随一个活动标架,该活动标架是一个直角坐标系,由单位切向量τ、单位法向量n和单位副法向量b组成,如图1所示。切向量的方向为质点沿曲线运动的方向,切向量随着弧长变化的方向为法向量的方向,通过切向量和法向量按照右手螺旋规则确定副法向量的方向。
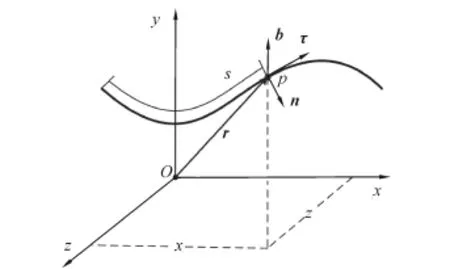
图1 空间中的曲线的描述方法Fig.1 Description of the curve in the space
在曲线上任意选取一段微元作为研究对象,参考构形和当前构形下的关系如图2所示。

图2 变形前后单元坐标Fig.2 Cable element in the reference configuration and deformed configuration
设参考构形下弧长为ds,当前构形下弧长为ds~,微元的轴向应变即为εl=∂s~/∂s-1,式中∂s~/∂s是一个标量,其物理意义为:在轴线上一点附近的微元在切向的伸长比。同时,由微分几何关系可知,单位切向量和总体坐标之间的关系为

式中:r′=∂r/∂s为斜率,s为变形前弧长。因此,微元的轴向应变可以写为

该式即为微元的非线性应变位移关系式。
本文采用有限元法研究锚泊线的求解问题。从曲线上选取一个单元作为研究对象,单元上任意一个质点的坐标通过形函数S和单元坐标q插值获得。锚链处于完全柔性状态,认为其在空间中连续、光顺,因此曲线保持节点坐标连续和坐标的一阶导数连续,是一条C1型曲线。
借助艾尔米特(Hermite)插值多项式,将任意质点的位置矢量写成r=Sq,式中S为形函数,q为单元节点坐标。形函数的表达式为
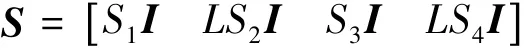
式中:I为单位矩阵。形函数的具体形式为

式中:ξ=s/L,s为单元弧长度。三维空间中单元节点坐标为

式中:

1.3 锚泊线能量变分法
由于锚泊线在外载荷的作用下发生了较大变形,因此不同于小变形情况,相关方程必须在变形后的状态下建立。为了充分利用已知的变形前的各项特征参数,在锚泊线静力计算方法中,通过变形前后弧长的映射关系,实现完全拉格朗日格式的平衡方程。
在静力分析中,锚泊线受到外力作用,产生相应的变形。通过能量守恒原理,可得总功W为零,即应变能WS等于外力功WE,有
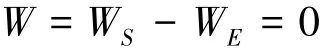
由于锚泊线的拉伸变形是主要的关注点,因此,将应变能展开成具体的形式,可将能量方程写为

通过对全量形式的方程两边取变分得到增量形式的方程,同时将外力功展开成分布外力作用的形式,有
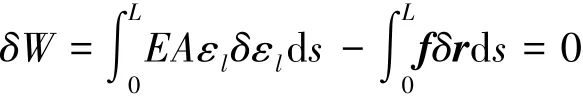
式中:f表示单位长度上施加的外载荷。引入有限元位移模式q,有变分关系式:

应用单元位移变分δq获得新形式的平衡方程:

此时,平衡方程可简写,整理有
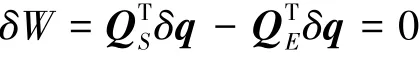

为求解方程组,整理出完整形式的切线刚度矩阵KT。按照此前轴向应变的定义εl=r′-1,同时借助高斯积分法即可较为方便地计算出该切线刚度矩阵。之后,按照标准有限元流程进行单元组装,使用牛顿法和高斯消去法求解即可获得结果。

因此,该模型是一个2节点单元,每个节点具有6个自由度,具有一阶导数连续的特性。单元内各处截面属性相同,重点涉及了锚泊线的单元长度、抗拉刚度和线密度等参数。由于锚泊线有钢链、钢缆、纤维缆等多种形式,其截面也各不相同,因此计算中需要采用等效的方法进行估算,如等效截面积,可通过厂商提供的锚泊线手册查得。单元长度由分析者在无拉伸状态下指定。节点初始自由度通过位置坐标给出即可,方便起见,可按某个角度下的直线给出,由迭代法计算得到平衡状态。
2 新理论与弹性悬链线的对比分析
因为锚泊线呈悬链形态,所以具有解析解的悬链线理论经常被用来校核相关理论是否准确。在此次分析中,轴向拉伸变形特性是主要的分析特征,所以本节将使用具有轴向拉伸特性的弹性悬链线理论与锚泊线理论进行对比分析。
2.1 可拉伸悬链线基本数据
假设悬链线顶端铰接,底端只受水平力作用,计算出悬链线的形态,通过悬链线水平投影、垂向投影分别与总链长比值的无量纲量对比计算结果的准确性,如图3所示。

图3 底端水平的悬链线Fig.3 Catenary line with tangent lower point
在这种情况下,底端只受水平力作用意味着锚链底端与海底相切,在触地点的水平力即为锚链的张力。根据触地点水平力的大小不同对比计算分为4种情况,每个张力下通过4组单元数量来验证程序的收敛性,通过与精确解的对比验证结果的准确性。
在本次分析中,选取一条锚泊线的参数作为计算数据,抗拉刚度4.35×107N,单位长度重力1 084 N/m,总长度3 536 m,计算收敛误差1.00× 10-11。锚泊线的初始形态按照水平直线给出,由程序计算出平衡状态下的位形和各点处的张力,完成平衡构形分析。在40个单元情况下各个张力下的悬链线形态如图4所示,从图中可以看出水平力越小,曲线越趋于垂直状态。其他相关计算结果如表1、2所示。

表1 水平段无量纲值的计算结果与解析解Table1 Comparison of calculated and analytical results on non-dimensional horizontal displacement

表2 垂直段无量纲值的计算结果与解析解Table2 Comparison of calculated and analytical results on non-dimensional vertical displacement
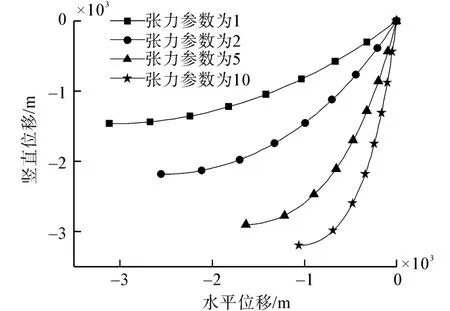
图4 各张力参数下悬链线形态Fig.4 The catenary shapes under different tensions
2.2 计算结果对比分析
从表1和表2中的结果可以看出,在各个工况下,随着单元数量的增加,计算结果不断趋近于精确解,表现出了一致的收敛性。在水平段无量纲值的第4种张力中,由于水平力较小,收敛性最为复杂,仅从前3组单元中很难判断结果的收敛情况。通过增加一组40个单元的计算可以看出,结果与20个单元的计算值逐渐趋于一致。与精确解相比也达到了小数点后6位的匹配度。
整体来看,在各种张力的计算中,程序表现出了较好的收敛性和较快的收敛速度。在水平段无量纲值的第1种情况下,1个单元的计算已经取得了小数点后3位的匹配度。随着单元数量增加到10个,结果可以吻合至小数点后7位,计算精度有了显著的提升。从表3和表4的相对误差分析中也可以看出,计算结果收敛迅速,10个单元的情况下计算结果已经趋于稳定。从图5和图6中可以看出,在本次计算中10个和20个单元已经取得较好的计算结果,因此在实际计算中,从节省计算资源的角度来看,10~20个单元是建议的取值范围。

表3 水平段无量纲值的相对误差Table 3 The relative errors for horizontal segment

表4 垂直段无量纲值的相对误差Table 4 The relative errors for the vertical segment

图5 各张力参数下水平段相对误差分析Fig.5 The relative errors of horizontal segment under tensions
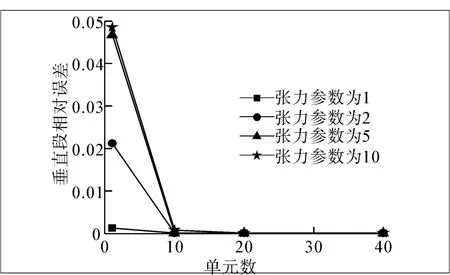
图6 各张力参数下垂直段相对误差分析Fig.6 The relative errors of vertical segment under tensions
4 结束语
总体坐标方法通过斜率代替转角坐标,克服了原先复杂的大变形问题描述过程,省去了单元局部坐标和全局坐标之间的转换,能方便地通过有限元法进行求解。同时,结合能量变分法和非线性几何方程较为准确地描述了轴向大拉伸问题。通过与弹性悬链线方法的对比结果可以看出,基于能量变分总体坐标法的锚泊线理论可以有效地应用于解决轴向大变形锚泊线问题。
[1]WEBSTER W C,LAMBRAKOS K,KIM J,et al.Rod dynamics with large stretch[C]//Proceedings of the ASME 2012 31st International Conference on Ocean,Offshore and Arctic Engineering.Rio de Janeiro,Brazil,2012.
[2]GARRETT D L.Dynamic analysis of slender rods[J].Journal of Energy Resources Technology,1982,104(4):302-306.
[3]LOW Yingmin,ROBIN S.Langley dynamic analysis of a flexible hanging riser in the time and frequency domain[C]//Proceedings of OMAE2006 25th International Conference on Offshore Mechanics and Arctic Engineering.Hamberg,Germany,2006.
[4]SUN Liping,HE Qiang,AI Shangmao.Safety assessment for a side-by-side offloading mooring system[J].Journal of Marine Science and Application,2011,10(3):315-320.
[5]孙丽萍,聂武.杆、梁结构振动能量密度的简化解法[J].哈尔滨工程大学学报,2004,25(4):403-406.SUN Liping,NIE Wu.A simplified method for solving energy density of rods and beams[J].Journal of Harbin Engineering University,2004,25(4):403-406.
[6]WANG Hongwei,LUO Yong,HU Kaiye,et al.Mooring truncation design of a deepwater spar[J].Journal of Marine Science and Application,2010,9(2):168-174.
[7]王宏伟,罗勇,苏玉民.悬链线式锚泊及立管系统等效截断设计[J].哈尔滨工程大学学报,2010,31(12):1565-1572.WANG Hongwei,LUO Yong,SU Yumin.Equivalent truncation design of catenary mooring and riser system[J].Journal of Harbin Engineering University,2010,31(12):1565-1572.
[8]田强,张云清,陈立平,等.柔性多体系统动力学绝对节点坐标方法研究进展[J].力学进展,2010,40(2):189-202.TIAN Qiang,ZHANG Yunqing,CHEN Liping,et al.Advances in the absolute nodal coordinate method for the flexible multibody dynamics[J].Advances in Mechanics,2010,40(2):189-202.
[9]ZHANG Jian,REN Huilong,ZHANG Lijie.A nonlinear restoring effect study of mooring system and its application[J].Journal of Marine Science and Application,2012,11(2):74-82.
[10]赵阳,范菊,袁梦,等.多刚体动力学在缆索动力分析中的应用[J].船海工程,2011,40(1):152-155.ZHAO Yang,FAN Ju,YUAN Meng,et al.Application of the multi-body system dynamics in the dynamic analysis of mooring lines[J].Ship&Ocean Engineering,2011,40(1):152-155.
[11]GERSTMAYR J,IRSCHIK H.On the correct representation of bending and axial deformation in the absolute nodal coordinate formulation with an elastic line approach[J].Journal of Sound and Vibration,2008,318(3):461-487.
Static analysis of the mooring line under large deformation by utilizing the global coordinate method
MA Gang,SUN Liping
(College of Shipbuilding Engineering,Harbin Engineering University,Harbin 150001,China)
To solve the defect of large axial stretching of the mooring line,a new solution jointly applying the global coordiantes,the energy variational principle and the finite element method have been proposed.The rotation angles were replaced by the slope of the node in the global coordinate,in order to make the description of the nonlinear relationship of the strain and the displacement.At the same time,mapping relationships of the parameters of the current and the reference configurations were set up.Then the equilibrium equations of the strain energy and externalforce work were created on the basis of the energy variational principle so as to form the element stiffness matrix of the mooring line.Finally,all the elements were assembled and solved by use of the numerical method.This new method shows a precise presentation of the deformation of the large rotation and the large stretch in the 3D,and no translation is needed between the element coordinates and the global coordinates when the assembling is performed.One comparison was executed with the extensible catenary theory which has the analytical resolution.The comparison results show that this new method has rapid convergency and good accuracy.
global coordinate method;energy variational principle;finite element method;mooring line;static analysis
10.3969/j.issn.1006-7043.201306006
http://www.cnki.net/kcms/doi/10.3969/j.issn.1006-7043.201306006.html
O33
A
1006-7043(2014)06-0674-05
2013-06-03.网络出版时间:2014-05-14 15:52:55.
国家高等学校学科创新引智计划资助项目(B07019);中央高校基本科研业务费专向资金资助(HEUCFD1402);高等学校博士学科点专项科研基金新教师类资助课题(20132304120008).
马刚(1984-),男,博士研究生;孙丽萍(1962-),女,教授,博士生导师.
马刚,E-mail:magang@hrbeu.edu.cn.

