基于Schmidt正交单位化的稀疏化定位算法
赵春晖,许云龙,黄辉,崔冰
(哈尔滨工程大学信息与通信工程学院,黑龙江哈尔滨150001)
基于Schmidt正交单位化的稀疏化定位算法
赵春晖,许云龙,黄辉,崔冰
(哈尔滨工程大学信息与通信工程学院,黑龙江哈尔滨150001)
为了提高在一个移动信标节点下的无线传感器网络节点定位的精度,提出了一种稀疏化的无线传感器网络节点定位算法。该算法通过网格化感知区域把节点定位问题转化为稀疏信号重构问题,并提出了Schmidt正交单位化的预处理方法,对观测矩阵进行预处理,使其有效地满足了约束等距性条件。并针对稀疏定位模型中得到的稀疏信号是近似稀疏信号的问题,采用质心算法来优化算法的定位精度。实验结果表明,相比于MAP类算法,稀疏化的无线传感器网络节点定位算法的定位精度更优,同时所需要的信标节点的广播次数也更少。
稀疏化定位;节点定位;压缩感知;Schmidt正交单位化;无线传感器网络;移动信标
无线传感器网络(wireless sensor network,WSN)是由随机分布在监测区域内大量的、廉价的、微型的传感器构成的多跳自组织网络。WSN以其低功耗、低成本、自组织和分布式等特点为信息感知带来了一场重大的变革。由于资源和成本的限制,在WSN的多数应用中,除了少数信标节点外,绝大多数节点的位置是未知的。然而,网络中传感器的布局、覆盖、目标定位[1]、目标追踪[2]等都离不开节点的位置信息,没有位置信息,网络的监测消息将毫无意义。因此,确定节点的自身位置是WSN实际应用过程中亟待解决的问题。
根据信标节点的类型,无线传感器网络节点定位算法可分为基于静态信标节点的定位算法和基于移动信标节点的定位算法。由于静态信标节点在网络中不能随机移动,为了使所有的节点都能被准确定位,网络需要布设大量的静态信标节点,这样就会使得系统的功率损耗和网络的硬件开销大大地增加。而移动信标节点在网络中可以动态的移动并在移动过程中广播位置信息,一个移动信标节点在网络中的作用等同于多个静态信标节点。因此,移动信标节点的使用能使网络成本得到有效地控制。WSN中,典型的基于移动信标节点的定位算法有基于测距[3]的定位算法、HADO[4]定位算法、MAP[5-7]类算法等。其中,基于测距的定位算法是利用节点间的距离信息估计节点的位置,由于算法依靠测距技术,因此需要附加额外的测距设备,增加了系统的硬件开销;HADO算法通过利用信标节点的到达和离开来估计节点的位置,然而该算法对移动信标节点的移动路径要求高;MAP类算法通过利用节点感知边界上的信标点来估计节点的可能位置,但是,该类算法的定位精度易受其选择的信标点影响。
本文提出了一种新的无线传感器网络节点稀疏化定位模型。通过网格化感知区域,将基于移动信标节点的无线传感器节点定位问题有效地转化为了压缩感知[8-9]的问题。在此基础上,针对观测矩阵不能满足RIP[9]问题,提出了Schmidt正交单位化的预处理方法,使得观测矩阵有效地满足RIP条件,保证了压缩感知算法的重构性能。最后,针对模型中信号不是严格的1稀疏信号的问题,采用了加权质心算法[10]来进一步改善节点的定位精度。
1 系统模型
1.1 稀疏化定位模型
假设一个节点在其感知区域内,能够监听到M个信标点的信号,则可利用这M个信标点来确定该节点的无线感知区域。将所确定的感知区域均匀地划分成N个网格,由于节点只会存在于其中的一个网格中,将该网格看作1,其他网格看作0。这样,就可以将节点的定位问题转化为稀疏度为1的N维向量的重构问题,此时,节点需要根据接收到的信标点的信号最终确定自身所在的网格位置。节点的稀疏化定位模型如图1所示。
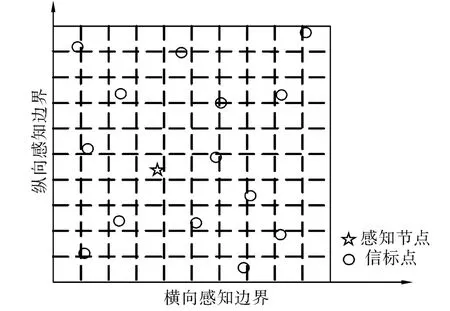
图1 稀疏化定位模型Fig.1 Sparse localization model
1.2 压缩感知算法
依据压缩感知[8-9]理论,未知信号X∈RN在测量矩阵AM×N(M≪N)的投影下,可转换为线性观测值Y∈RM如下:

压缩感知的最终目标是将方程组(1)中的未知信号X准确的重构出来。由于上式中Y的维数M远小于信号X的维数N。因此,此方程组为欠定线性方程组,即方程组有无穷多解。
压缩感知[8]理论认为:若X为k稀疏的信号,且测量矩阵AM×N满足RIP条件,则信号X的精确重构可通过求解一个l1范数最小化的问题获得,过程如式(2)所示:
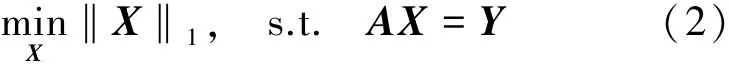
在稀疏化定位模型中,测量矩阵A中第m行第n列元素表示的是第m个信标点到第n个网格中心点的信号接收强度RSSm,n。这样,稀疏度为1的信号X的压缩采样过程可描述如下:

式中:yi(1≤i≤M)为节点接收到第i个信标点的信号强度;在定位模型中,若节点存在于第n个网格中,则xn=1,其余为0。显然,未知信号X是1稀疏的。这样,通过网格化感知区域,节点定位问题就变成了稀疏信号X的重构问题了。
2 SLSO定位算法
2.1 Schmidt正交单位化预处理
由于测量矩阵A是通过信标点与网格之间的信号衰减模型得到,因此,A中元素较为相关,即无法满足等距约束条件。为此,本文利用Schmidt正交单位化对测量矩阵进行预处理,得到的新的测量矩阵能有效地满足RIP条件,从而保证算法的重建性能。
Schmidt正交单位化预处理包括正交化和单位化2个过程。首先,正交化测量矩阵A的过程如式(4)所示:

式中:A1,A2,…,AM为测量矩阵A的行向量,且有Am=[RSSm,1,RSSm,2,…,RSSm,N]表示第m个信标点到每一个网格中心点的信号接收强度;〈·,·〉表示内积算子;T是一个对角线元素全为1的下三角矩阵;通过正交化后得到矩阵B的正交向量组B1,B2,…,BM。然后,对矩阵A进行行单位化得

式中:‖·‖指的是矩阵的模值。因此,矩阵Q是行向量相互正交的单位向量。
最后,列单位化矩阵Q,即得新的测量矩阵Φ如下:

式中:Q1,Q2,…,QN为矩阵Q的列向量。由于Q的行向量是相互正交的单位向量,且Φ是通过列单位化Q得到。因此,Φ是压缩感知理论中常用的观测矩阵之一的部分正交矩阵[8]。换句话说,Φ是完全满足等距约束条件的。
令T1=diag(‖B1‖,‖B2‖,…,‖BM‖)。对观测值Y进行下面的变换可得新的观测值Y′:
Y′=(TT1)∗Y=(TT1)∗AX=(TT1)∗TT1QX=
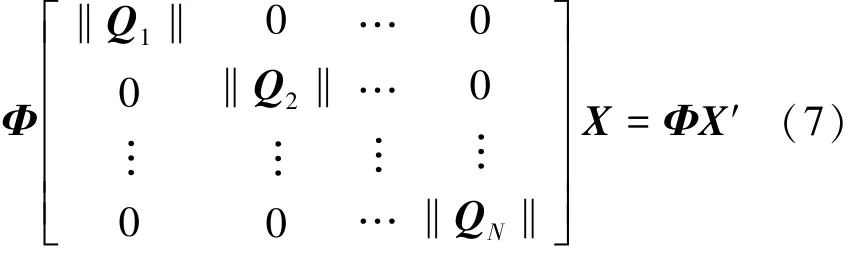
式中:(·)∗表示矩阵的逆运算。由式(7)可知:

显然,X′是由矩阵X左边乘一个对角矩阵得到,由于稀疏化定位模型中的未知信号X是稀疏的,因此X′也是稀疏的,且其稀疏度与X相等。又由于Φ完全地满足等距约束条件,因此,X′能够依据压缩感知理论被准确地重构出来,这样,原信号X也就被确定了。
2.2 节点位置估计
在稀疏化定位模型中,理论上将每个网格的中心位置作为该网格的坐标。然而,在实际的WSN应用场景中,节点是随机分布的,换句话说,节点的位置不一定在网格的正中心。因此,实际的X应该是一个近似的稀疏度为1的稀疏信号。为了减小定位误差,本文采用加权质心算法[10]估计节点的位置。
首先,归一化信号X,得到每个网格对该节点估计位置的权值ωn:

式中:ωn为第n个网格对该节点估计位置的权值大小。然后,利用加权质心算法求解该节点的估计位置,如式(10)所示:
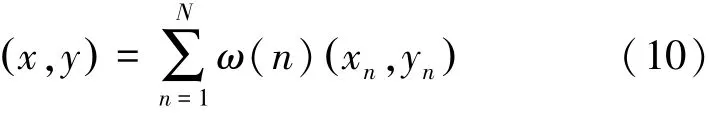
式中:(x,y)表示节点的估计位置,(xn,yn)表示第n个网格的中心所在的位置。
2.3 感知区域的确定
稀疏化定位模型首先需要对节点的感知区域进行网格化,因此,节点感知区域的确定是节点定位的基本前提。然而,WSN中待定位的节点自身是无法确定其感知区域的,这时,在节点感知区域内的一些位置信息已知的信标点则能发挥其关键作用,即可利用这些信标点来确定节点的感知区域。为了使节点感知区域的覆盖范围尽可能的小,MCB(monte carlo localization boxed)定位算法[11]利用信标盒子的思想对感知区域进行确定。然而,该信标盒子并没有将所有的信标点包含到感知区域内。因此,为更准确地确定感知区域坐标,本文对其进行如下改进:

式中:xmin、xmax、ymin、ymax分别表示感知区域的x轴,y轴坐标的最小值和最大值;xi和yi分别为第i个信标点的x轴和y轴坐标;r为节点的通信半径;M是节点感知到的信标点的个数。
2.4 信标点个数的选择
由于在感知区域内,节点能感知到的信标点的个数可能非常多,这将给普通节点带来很大的计算负担。此外,由文献[8]可知:当M大于等于O(C· k·μ2·(logN)4)时,算法已经能准确地重建出原信号,其中k是信号的稀疏度,C是一个常数,μ=Nmax |Φi,j|,这也就是说,信标点个数达到一定
i,j值后,过多的信标点对节点定位精度的提升并不明显。因此,合理的选择信标节点个数是非常必要的。为便于合理取值信标点个数,本文把普通节点的稀疏化定位模型抽象成为在一个方形的无线感知区域内定位某一固定目标的问题。
假设在一个20 m×20 m的方形感知区域内,随机地分布着M个传感器,将感知区域均匀地网格化为15×15的小格子。则在信标点的发射信号强度为-40 dBm,信噪比为20 dB的环境下,对2~10的每一个固定的M值进行100次仿真,取节点定位误差的平均值作为其平均定位误差,得到如图2所示的目标平均定位误差随传感器个数M变化的曲线。从图中曲线可以看出:节点的平均定位误差随传感器个数M的增加而降低。然而,当传感器个数M≥4时,目标的平均定位误差均保持在0.5 m左右;当M≥8时,目标的平均定位误差已基本无变化。
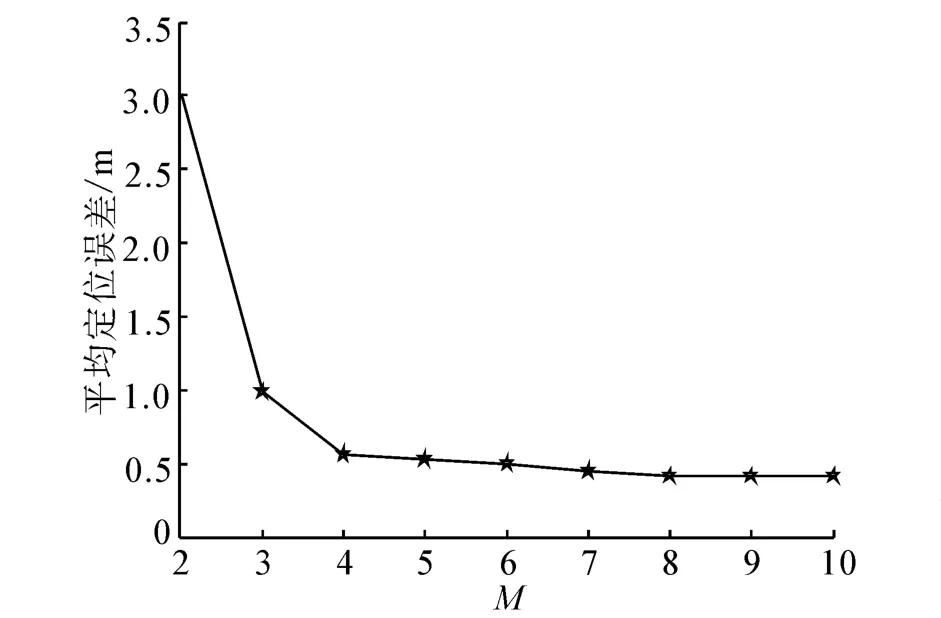
图2 定位精度与传感器个数的关系Fig.2 Relationship between localization accuracy and number of nodes
3 仿真结果和分析
为了验证算法的有效性,利用MATLAB对SLSO算法进行了仿真,并将其与MAP+GC[6]、MAPM[7]和MAP-M&N[7]算法的定位精度进行对比。其中,假设在一个边长为100 m的方形感知区域内随机地分布着1 000个普通节点,网络中所有的普通节点和信标节点的通信半径均为20 m,信标节点最大移动速度为20 m/s,且其移动路径遵循RWP[12]模型。此外,在SLSO算法中,将节点感知区域均匀地划分为15×15的网格,信标点的发射信号强度为-40 dBm,信噪比为20 dB。当节点感知到的信标点个数大于或等于8时,则取其中信号强度最强的8个信标点进行定位,即M=8,否则M为实际感知到的信标点个数。在SLSO算法中,设定信标节点每1 s广播一次信标信号,广播400次。而在MAP类算法中,由于信标点广播间隔太大会影响定位精度,因此,设定信标节点每0.1 s广播一次信标信号,广播10 000次。
本文采用文献[13]中的信号衰落模型,则有距离信号源为d时感知节点接收到的信号强度为

式中:Pt为距离信号源节点为d0的节点接收到的信号强度,η为衰减指数,通常取2~4,本文取2。
3.1 理想环境下的定位精度对比
在MATLAB仿真环境下,对SLSO、MAP+GC、MAP-M和MAP-M&N 4中算法在理想环境中的节点位置误差进行对比如图3所示。图3中的圆圈表示该节点未被定为到。通过比较可以看出:SLSO算法定位的大部分节点定为误差均小于5 m,即使最大的误差也只有15 m左右。而MAP类定位算法中,有较多的节点存在很大的定位误差,最大的甚至超过了30 m。此外,MAP类算法即使信标节点广播了10 000次,也依然存在定位不到的节点。这是由于MAP类算法需要选择合适的信标点进行定位,否则会对节点定位产生较大的影响,甚至在没有合适的信标节点的情况下,无法完成节点的定位。而SLSO算法只有当接收到的信标点较少时,其定位精度才会较差,并且算法对信标点没有特定的要求。


图3 算法定位精度对比Fig.3 The localization accuracy comparison
3.2 通信半径对定位精度的影响
如表1所示定量的比较了理想环境中4种算法在不同的通信半径下的定位精度。从表中数据可以看出:在相同的节点通信半径下,SLSO算法的平均定位误差远小于MAP类算法。此外,对同一种定位算法而言,随着通信半径的增加,节点的平均定位误差也在逐渐的增加,这是由于半径增大,对节点的约束性越来越小,因此误差也越来越大。

表1 通信半径对算法定位精度的影响Table1 The impact of radio range on the localization accuracy
3.3 障碍物环境下的定位精度对比
在实际WSN应用环境中,节点定位往往会受到各种障碍物的影响,因此,本节将进一步的分析算法在障碍物环境下的定位精度。障碍物环境下的节点分布图如图4所示。
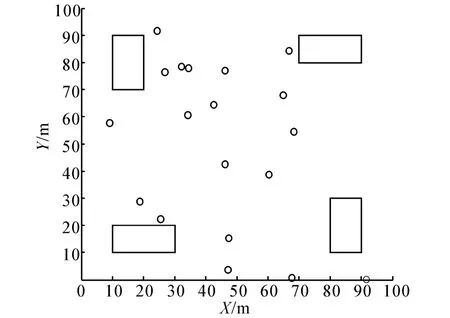
图4 障碍物环境下的节点分布图Fig.4 The distribution of nodes with obstacles
在如图4所示的障碍物环境下,对4种算法的定位精度进行MATLAB仿真实验,得到如表2所示的障碍物环境下各算法的平均定位误差。

表2 障碍物环境下算法的定位精度对比Table 2 The localization accuracy comparison under obstacle environment
从表2中数据可知:即使在障碍物环境下,SLSO算法的节点平均定位误差依然要远小于MAP类算法,也就是说,相比于MAP类算法,不论是在理想环境下还是在存在障碍物的环境中,SLSO算法都是一个更好的选择。此外,通过对比表1和表2可以看出:在障碍物存在的情况下,MAP类算法的性能下降的比较厉害,而SLSO算法的平均定位误差波动不大。这是MAP类算法中靠近障碍物的节点选择了错误的信标点,这样,会影响其弦方位,进而影响到节点的定位精度,其中在MAP-M&N算法中表现尤甚,这是因为其节点定位本身存在着定位误差,而该算法还利用了这些存在定位误差的已定位节点去定位其他还未被定位的节点,因此其很有可能会错误的选择节点可能位置。而在SLSO算法中,障碍物的存在仅使得靠近障碍物的节点所能接收到的信标点个数减少了,因此其定位精度仅受到较小的影响。
3.4 GPS定位误差对定性性能的影响
WSN中,信标节点依赖于GPS设备进行自身的定位,然而,实际应用中GPS设备往往也会存在一定的定位误差。在信标节点GPS误差标准差为0.05 m,GPS误差均值分别为0、0.1、0.2、0.3、0.4 m时,对4种算法的定位精度进行仿真实验对比如图5所示。由图中曲线可知:4种算法的定位精度均随着GPS平均定位误差的增大而缓慢的降低。而在相同的GPS误差均值的条件下,SLSO算法在平均定位误差要远优于MAP类算法。此外,通过表1和图5可以看出:信标节点的GPS误差对算法的定位精度并没有较大的影响。

图5 GPS误差对定位精度的影响Fig.5 The impact of GPS error on the localization accuracy
3.5 通信半径不规则性对定性性能的影响
在实际环境中,节点的通信半径具有一定的不规则性(degree of irregularity,DOI)。DOI是指节点的最大通信半径在不同的角度和方向上具有不同程度的衰减,衰减因子[14]如下:

其中:K0-K359≤DOI。
图6对比分析了通信半径的不规则性对算法定位精度的影响。

图6 定位精度与通信半径的不规则度的关系Fig.6 Relationship between localization accuracy and DOI
图中曲线表明:4种算法的定位精度均随着通信半径不规则度的增大而降低。而在相等的通信半径不规则度下,SLSO算法的平均定位误差远小于MAP类算法。此外,通信半径不规则度对SLSO算法的影响远小于MAP类算法。这是由于SLSO算法采用的是信号接收强度进行节点定位,因此通信半径的不规则性对其基本上没什么影响,而MAP类算法需要利用通信半径估计节点的位置,因此通信半径的不规则性,将会严重地影响算法的定位精度。
3.6 噪声对定位精度的影响
如表3所示是在不同信噪比下仿真了SLSO算法的定位精度。由表中数据可知:算法的平均定位误差随着信噪比的增大而不断减小,即算法的定位精度越来越好。这是由于信噪比越大,节点接收到的信号强度越准确,因此算法的性能越好,反之亦然。同时,通过对比表3和表1可知:即使在0dB的信噪比环境下,SLSO算法的定位精度仍优于MAP类算法。因此,在复杂环境下,SLSO算法仍然是一个较好的选择。

表3 噪声对SLSO算法定位精度的影响Table 3 The impact of noise on SLSO localization accuracy
4 结束语
本文提出了基于Schmidt正交单位化的稀疏化定位算法。首先,算法通过网格化感知区域,首次把只存在一个移动信标节点的无线传感器网络的节点定位问题转换为了稀疏度为1的N维向量重构问题;然后,为使测量矩阵完全有效地满足RIP性质,提出了Schmidt正交单位化的预处理方法,保证了算法的压缩感知重建性能;最后,利用质心算法准确地估计节点位置。仿真结果表明:相比于MAP类算法,SLSO算法有更小的平均定位误差,也就是说,SLSO算法的定位精度远优于MAP类算法。与此同时,定位所有的节点,SLSO算法需要的信标点个数远少于MAP类算法,且障碍物和通信半径不规则性对SLSO算法无明显影响。并且,在信噪比很低的情况下,SLSO算法仍然优于MAP类算法。因此,SLSO算法具有更强的适应性和实用性。
[1]赵春晖,许云龙.能量约束贝叶斯压缩感知检测算法[J].通信学报,2012,33(10):1-6.ZHAO Chunhui,XU Yunlong.Energy constraint Bayesian compressive sensing detection algorithm[J].Journal on Communications,2012,33(10):1-6.
[2]WANG Xingbo,FU Minyue,ZHANG Huanshui.Targettracking in wireless sensor networks based on the combination of KF and MLE using distance measurements[J].IEEE Transactions on Mobile Computing,2012,11(4):567-576.
[3]SICHITIU M L,RAMADURAI V.Localization of wireless sensor networks with a mobile beacon[C]//IEEE International Conference on Mobile Ad-hoc and Sensor Systems.Raleigh,USA,2004:174-183.
[4]XIAO Bin,CHEN Hekang,ZHOU Shuigeng.Distributed localization using a moving beacon in wireless sensor networks[J].IEEE Transactions on Parallel and Distributed Systems,2008,19(5):587-600.
[5]SSU K F,OU C H,JIAU H C.Localization with mobile an
chor points in wireless sensor networks[J].IEEE Transac
tions on Vehicular Technology,2005,54(3):1187-1197.[6]LEE S,KIM E,KIM C,et al.Localization with a mobile beacon based on geometric constraints in wireless sensor networks[J].IEEE Transactions on Wireless Communications,2009,8(12):5801-5805.
[7]LIAO W H,LEE Y C,KEDIA S P.Mobile anchor positioning for wireless sensor networks[J].IET Communications,2011,5(7):914-921.
[8]CADES E.Compressive sampling[J].International Congress of Mathematicians,2006,3:1433-1452.
[9]CADES E,PLAN Y.A probabilistic and RIP less theory of compressed sensing[J].IEEE Transactions on Information Theory,2011,57(11):7235-7254.
[10]WANG Jun,URRIZA P,HAN Yuxing,et al.Weighted centroid localization algorithm:theoretical analysis and distributed implementation[J].IEEE Transactions on Wireless Communications,2011,10(10):3403-3413.
[11]ALINE B,KOEN L.Monte-Carlo Localization for mobile wireless sensor networks[J].Ad Hoc Networks,2006,6(5):718-733.
[12]BROCH J,MALTZ D A,JOHNSON D B,et al.A performance comparison of multi-hop wireless Ad hoc network routing protocols[C]//ACM International Conference on Mobile Computing Networking.Dallas,USA,1998:85-97.
[13]PATWARI N,ASH J N,KYPEROUNTAS S,et al.Locating the nodes:cooperative localization in wireless sensor networks[J].IEEE Signal Processing Magazine,2005,22(4):54-69.
[14]HE T,HUANG C,BLUM M B,et al.Range-free localization schemes for large scale sensor network[J].ACM Transactions on Embedded Computing System,2005,4(4):877-906.
Sparse localization on the basis of Schmidt orthonormalization in wireless sensor networks
ZHAO Chunhui,XU Yunlong,HUANG Hui,CUI Bing
(College of Information and Communication Engineering,Harbin Engineering University,Harbin 150001,China)
To improve the localization accuracy of a node in the wireless sensor network with a mobile beacon node,a sparse localization algorithm using Schmidt orthonormalization(SLSO)was proposed.With the SLSO,the node localization problem was converted to a reconstruction problem of the sparse signal by gridding the sensing area,and a new observation matrix which is able to effectively satisfy the restricted isometry property(RIP)was obtained by Schmidt orthonormalization.To solve the problem of the sparse signal being approximately sparse in the model,a centroid algorithm was adopted to improve the localization accuracy.The experiment results show that,compared with MAP algorithms,SLSO has better localization accuracy,and requires less broadcasting times.
sparse localization;node localization;compressed sensing;Schmidt orthonormalization;wireless sensor network;mobile beaconing
10.3969/j.issn.1006-7043.201305076
http://www.cnki.net/kcms/doi/10.3969/j.issn.1006-7043.201305076.html
TP393
A
1006-7043(2014)06-0747-07
2013-05-30.网络出版时间:2014-05-14 15:53:57.
国家自然科学基金资助项目(61077079);黑龙江省自然科学基金资助项目(ZD201216);哈尔滨市优秀学科带头人基金资助项目(RC2013XK009003).
赵春晖(1965-),男,教授,博士生导师.
赵春晖,E-mail:zhaochunhui@hrbeu.edu.cn.

