迭代寻优的稳健波束形成
王燕,吴文峰,范展,梁国龙
(哈尔滨工程大学水声技术重点实验室,黑龙江哈尔滨150001)
迭代寻优的稳健波束形成
王燕,吴文峰,范展,梁国龙
(哈尔滨工程大学水声技术重点实验室,黑龙江哈尔滨150001)
针对导向矢量失配程度较大时,常见稳健波束形成算法性能下降问题,提出了一种迭代搜索最优导向矢量的稳健波束形成算法。首先利用修正后的导向矢量构造使波束输出功率最大的目标函数,分别从干扰抑制和噪声抑制2个方面推导了新导向矢量应满足的约束条件。给出了利用矩阵滤波思想构造约束条件的方法并分析其合理性。针对优化问题难以求解的问题,提出了一种迭代寻优的搜索方法,将每次迭代转化为求解一次二阶锥规划问题。仿真分析表明,相比于常见稳健波束形成算法,该算法有更高的抗导向矢量失配的稳健性,且需要的先验信息更容易获取。
稳健自适应波束形成;矩阵滤波器;迭代优化;二阶锥规划;导向矢量
自适应波束形成在无线电通信、声呐、雷达、医学成像等领域有广泛的应用[1]。标准Capon波束形成器(standard Capon beamformer,SCB)[2]是理想条件下阵增益最高的处理器。但是SCB算法是建立在阵列对期望信号响应精确已知的假想基础上,在实际应用中不可避免存在观测方向误差、阵型标定误差、快拍数有限等条件失配情况,此时SCB算法会将实际期望信号误作干扰[3-4],导致信号自消现象。基于特征空间的波束形成方法(eigen-space projection,ESP)[5]和对角加载类算法是提升SCB算法稳健性的常用方法。ESP方法需要精确已知信号子空间的维数,且在低信噪比情况下失效。Li等提出的稳健Capon波束形成算法(robust Capon beamforming,RCB)等[6-9]都属于对角加载算法,但在导向矢量失配程度较大时,这些算法对干扰的抑制能力受到限制[7]。Hassanien等提出的基于二次规划的稳健波束形成(sequential quadratic programming,SQP)[10]能在给定区间内搜索最优导向矢量,但算法中过多的参数设置使算法的性能很难达到最优。针对标准Capon波束形成器在存在条件失配时,特别是失配程度较大时性能严重下降问题,提出了一种迭代寻优的稳健波束形成(iterative optimization robust Capon beamforming,IO-RCB)算法,该算法首次使用矩阵滤波思想构造约束条件,惟一的先验信息是期望信号可能的入射区间。本文提出的算法可以减小声呐系统等在实际应用中受环境和条件失配的影响。
1 稳健波束形成算法
考虑M元均匀线阵,阵元间距为半波长,K+1组窄带平面波(一组信号和K组干扰)从Θ=θ0θ1… θK]方向入射到基阵,信号、干扰与噪声均互不相关,则基阵接收数据协方差矩阵为
[


式中:w∈CM×1为待优化权值,as为预设导向矢量。针对SCB算法在实际应用中性能下降问题,文献[6]提出了稳健Capon波束形成方法(RCB)。假设期望信号的真实导向矢量属于如下不确定集:

则RCB波束形成器可以表述为
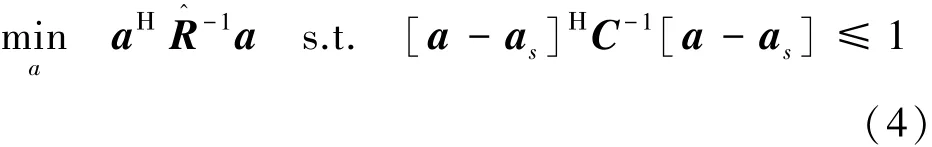
式中:C为用户设定的正定矩阵。RCB算法的性能不仅依赖于导向矢量不确定集的估计精度,且在导向矢量失配程度较大时严重退化。
2 迭代寻优的稳健波束形成算法
2.1 目标函数和约束条件的构造
对式(2)中的预设导向矢量作如下修正:

式中:Q∈CM×(M-1)为列满秩阻塞矩阵,满足QΗas=0且QΗQ=I;η∈CM-1为待求向量。利用新的导向矢量下,式(2)中的目标函数变为
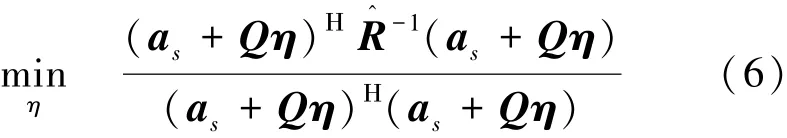
式(6)中对as+Qη归一化是为了防止尺度模糊。新导向矢量需满足如下2个约束:1)在期望信号功率小于干扰功率时不能指向干扰方向,且对干扰的抑制能力不能降低;2)不能放大基阵的噪声成分,即不能降低对噪声的抑制能力。下面分别从这2个约束讨论,训练数据中不含期望信号成分且快拍数足够大时,式(2)中权向量可以写成[11]


式中:γm(m=1,…M)为Ri+n按降序排列的特征值,满足γ1≥…≥γK≥γK+1=…=γM,um为对应的特征向量。γmin表示最小的特征值。wSCB对应的波束响应可以表示为式中:a(θ)表示基阵对θ方向的导向矢量;pm(θ)=uΗma(θ)为第m个特征波束,即以第m个特征向量作为加权向量得到的波束响应;ρm=aΗsum可视为调节因子。文献[11]指出,特征向量是正交的,特征波束间也是相互正交的,且在干扰方向ρm通过调节pm(θ)的大小使ρmum(θ)=aΗsa(θ)。因此wSCB对第k个干扰的响应为
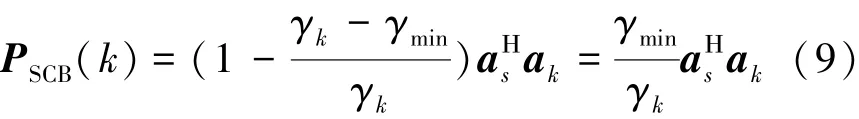
若要保证新导向矢量对应权值对干扰方向抑制能力不降低,必须有

式(10)显然也可以保证新的导向矢量不会指向干扰方向。
令Θs表示期望信号可能出现的扇面(区域大小和预处理精度有关),Θp表示其补集。若要保证新导向矢量对噪声不放大,需满足[10]
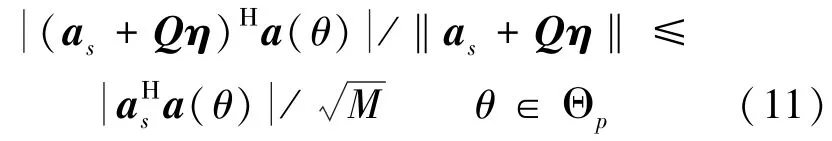

由于干扰信号真实方向未知,同时为了全局优化,结合式(10)和式(11)可得式中:δθ表示θ方向噪声功率的平方根。利用δk和δθ作为加权是为了保证对功率越大的干扰或噪声的抑制能力越强。利用干扰、噪声间互不相关,式(12)等价于:

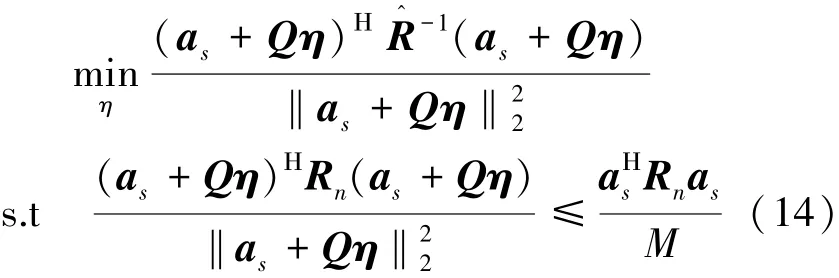
2.2 Rn的构造
本节以矩阵滤波原理[12]为基础,给出一种适合存在导向矢量误差时特定区域干扰和噪声协方差矩阵的重构方法,将Θs扇面设为矩阵滤波器的阻带,并离散化为θi(i=1,2,…,Ns);同时将Θp设为矩阵滤波器的通带,并离散化为θj(j=1,2,…,Np)。按阻带约束通带最小均方误差准则,矩阵滤波器优化问题可以表述为
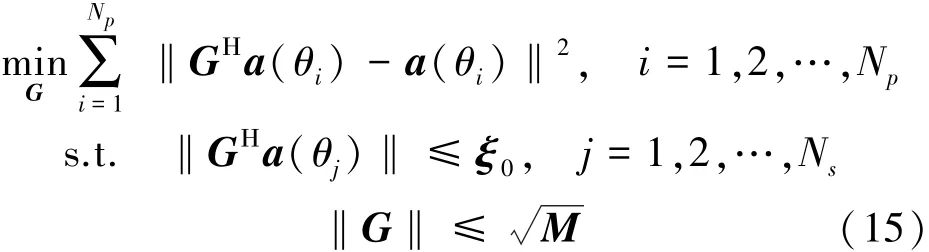
式中:ξ0为人为设定的阻带扇面内衰减率。式(15)可以转化为二阶锥规划问题[13]利用Sedumi或CVX等工具箱求解。
现验证利用式(15)设计的矩阵滤波器对存在导向矢量误差时的适用性。期望信号导向矢量误差由观察方向误差和随机误差组成,而对干扰只需考虑随机导向矢量误差,不妨设
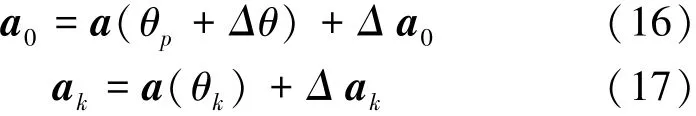
式中:θp为观测方向,Δθ为观测方向误差,Δ a0和Δ ak分别为随机导向矢量误差。利用Rayleigh商的性质可得
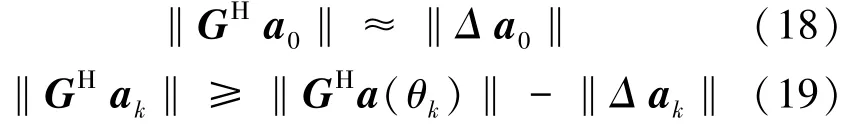
一般导向矢量误差的范数‖Δ a0‖≪‖a(θ0)‖,由式(18)知矩阵滤波器对真实信号仍具有抑制能力。同样式(19)中‖Δ ak‖≪‖GΗa(θk)‖,即第2项对第1项影响较小,矩阵滤波器仍能保证干扰近似无失真通过。综上存在随机导向矢量失配时,矩阵滤波器仍具有一定空域的滤波能力,滤波能力和随机导向矢量误差范数大小有关。
下面由一个数值仿真说明,考虑12元均匀线阵离散阻带设定为Θs=[5°∶1°∶15°],通带设定为Θp=[-90°∶1°∶-5°]∪[25°∶1°∶90°],阻带衰减设为-30 dB,利用式(15)设计滤波器。
图1分别显示理想情况和存在随机导向矢量误差时矩阵滤波器幅度响应,其中随机导向矢量误差为服从均值为0,方差为δ2I(δ=0.1)复高斯分布。从图1可以看出存在随机导向矢量误差时,阻带衰减虽减少但仍小于-21 dB,且通带起伏不超过0.3 dB,这和利用式(18)和式(19)估计结果吻合。

图1 矩阵滤波器幅度响应Fig.1 Magnitude response of the matrix filter
存在随机导向矢量失配时,矩阵滤波器仍具有一定的空域滤波能力,因此Θp扇面内的干扰和噪声协方差矩阵可由下式重构:

2.3 问题的求解
式(14)无法直接求得最优解,下面给出一种迭代寻优的方法。忽略尺度模糊的影响,则式(14)转化为

式(21)为二次约束二次规划问题,易转化为二阶锥规划问题求解。迭代寻优的具体步骤如下:
1)令上次迭代获得的最优导向矢量为as,求对应于as的阻塞矩阵Q,并求解式(21)获得η。
2)对新导向矢量as+Qη进行归一化

若迭代终止时获得最优导向矢量为a^s,则IORCB算法权值为
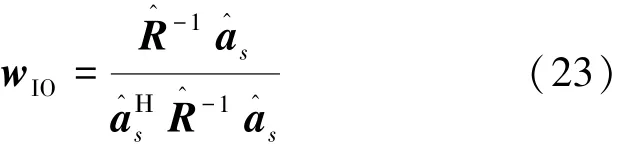
3 仿真分析
为了对比各算法的性能设计了以下几组实验。考虑12元均匀线阵,阵元间距为半波长。两组干扰分别从-30°和35°方向入射到基阵,干噪比分别为20 dB和25 dB,期望信号入射方位在[5°,15°],信号、干扰和噪声均为互不相关的窄带随机过程。对下述方法进行了对比分析:SCB算法、固定对角加载算法FDL、HKB算法[8]、GLC算法[9]、ESP算法、RCB算法和联合处理SQP算法[10],其中FDL算法固定对角加载量为10倍白噪声功率,对ESP算法而言假设信号子空间维数精确已知,SQP算法的参数同文献[10],RCB算法中的不确定集选取为球形且参数ε根据实际情况按文献[7]计算。所有仿真结果除波束图外均为200次Monte-Carlo实验取平均值,κ=10-5,除3.4节外矩阵滤波器设计参数均同2.2节。
3.1 波束图的对比
考察存在导向矢量失配时,各算法的波束图(只显示SCB、RCB和本文方法)。期望信号信噪比为20 dB,入射方向为13°,波束观测方向为10°,即存在3°观测方向误差,随机导向矢量误差Δa为服从均值为0、协方差矩阵为δ2I(δ=0.1)的复向量。快拍数取200,RCB算法参数ε=4.3。图2显示各算法波束图,其中垂直虚线表示信号和干扰的实际入射方向。
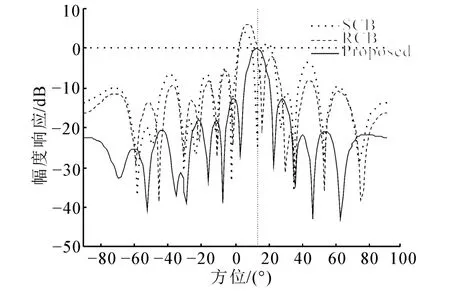
图2 存在导向矢量失配时波束图Fig.2 Beam-pattern in the presence of look direction error and random steering vector error
从图2可以看出RCB算法主瓣峰值未对准实际信号方向,虽然保证了整个不确定集内响应均大于0 dB,但也导致对干扰和噪声的抑制能力降低。本文算法主瓣峰值自动对准期望信号方位,且干扰零陷深度和对旁瓣的抑制能力高于RCB算法。
3.2 对快拍数不足稳健性的对比
考虑快拍数有限时各算法的性能。期望信号入射方位为10°,信噪比为20 dB,快拍数从12到204以阵元数为间隔变化,暂不考虑其他失配的情况。RCB算法中的参数取0.3 M。
图3显示各算法输出信干噪比随快拍数变化曲线。从图3可以看出,当快拍数为1 M时,本文算法的性能略低于RCB算法,但仍高于其他算法。在快拍数大于4 M后,本文算法性能优于其他所有算法。在快拍数较小时本文算法性能相对较低的原因是,由于快拍数不足引起的数据协方差矩阵误差可以看作由随机导向矢量误差引起,快拍数很低时等效的随机导向矢量误差较大,正如2.2节中的分析,此时矩阵滤波器的滤波效果受随机导向矢量误差限制,因此导致本文算法性能在低快拍时受限。
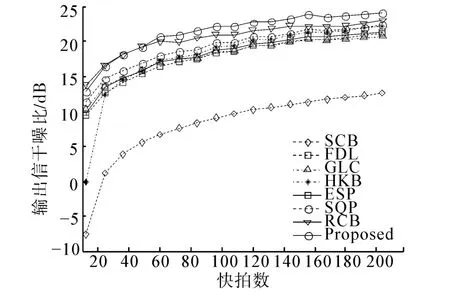
图3 输出信干噪比随快拍数的变化曲线Fig.3 Output SINR versus the number of snapshot
3.3 对观测方向误差稳健性的对比
波束观测方向固定为10°,实际信号入射方向在[5°,15°]以1°为间隔变化,期望信号信噪比为10 dB,快拍数取200,不考虑随机导向矢量误差的影响。图4显示各算法性能随观测方向误差变化曲线。从图4中可以看出,随观测方向误差的增加,本文算法和ESP算法的性能几乎没有下降,且本文算法的性能优于ESP算法。本文算法对观测方向误差稳健性较高的原因在于主瓣能自适应指向信号实际入射方向。
图4 各算法性能随观测方向误差变化曲线Fig.4 Output SINR versus look direction error
3.4 导向矢量失配对算法性能影响对比
考虑同时存在观测方向误差和随机导向矢量误差时算法性能。期望信号入射方位为13°,波束观测方向为10°,随机导向矢量误差同3.1节,快拍数取200,RCB算法参数取5。图5显示存在导向矢量失配时各算法性能曲线。从图5可以看出在整个观测区间内本文算法性能均优于其他算法。
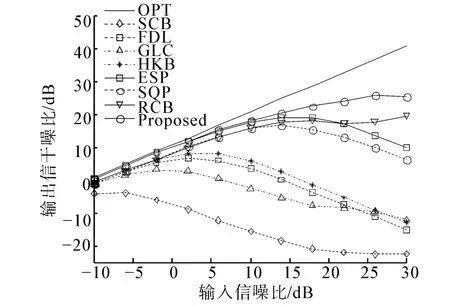
图5 输出信干噪比随输入信噪比的变化曲线Fig.5 Output SINR versus SNR
3.5 矩阵滤波器参数对算法性能的影响
本节将考察阻带区域的设置对本文算法性能的影响。实际信号入射方向为13°,且存在3.1节所述随机导向矢量误差,快拍数取200。波束指向方位θp=10°,矩阵滤波器的阻带设置为[θp-α,θp+ α],过渡带区域间隔设置为10°,阻带衰减为-30 dB。图6显示α取不同值时本文算法的性能。
从图6可以看出,当实际信号入射方位在阻带内时,阻带区域设置越小本文算法的性能越好,α适当偏大对本文算法影响不大。当滤波器阻带设置小于观测方向误差(α=2°时),算法性能在期望信号输入信噪比较大时略有降低,此时本文算法仍然有效的原因是是矩阵滤波器的过渡带仍有部分滤波作用。

图6 阻带区域设置对算法性能的影响Fig.6 The performance of the proposed algorithm under different parameters
5 结论
针对导向矢量失配程度较大时,常见稳健波束形成算法性能下降问题,提出了一种迭代搜索最优导向矢量的稳健波束形成算法。推导了新的目标函数和约束条件,并针对该优化问题难以求解问题,给出了一种迭代寻优解。仿真分析结果表明:
1)本文算法唯一利用的先验信息是期望信号可能的入射区间,且对先验信息的精度要求不高,相对于基于不确定集的稳健波束形成算法,该先验信息较易获取;
2)存在观测方向误差时,本文算法能将主瓣峰值指向实际信号入射方向,对观测方向误差有较高稳健性;
3)随机导向矢量误差对矩阵滤波器效果有一定影响,但本文算法对随机导向矢量误差的稳健性能满足实际应用需求;
4)和目前较为常见算法相比,本文算法能获得更高的输出信干噪比。
参考文献:
[1]陈阳,惠俊英.声矢量阵导向最小方差波束形成算法研究[J].哈尔滨工程大学学报,2008,29(11):1199-1204.CHEN Yang,HUI Junying.Acoustic vector sensor array steered minimum variance beamforming[J].Journal of Harbin Engineering University,2008,29(11):1199-1204.
[2]JIN W,JIA W M,YAO M L,et al.Robust adaptive beamforming based on iterative implementation of worst-case performance optimization[J].Electronics Letters,2012,48(22):1389-1391.
[3]武思军,张锦中,张署.存在指向性误差时的稳健自适应波束形成算法[J].哈尔滨工程大学学报,2005,26(4):531-535.WU Sijun,ZHANG Jinzhong,ZHANG Shu.Robust adaptive beamforming against pointing error[J].Journal of Harbin Engineering University,2005,26(4):531-535.
[4]刘凯,梁国龙,稽建飞.随机阵列误差影响下的声矢量阵噪声特性和阵增益[J].哈尔滨工程大学学报,2011,32(5):624-631.LIU Kai,LIANG Guolong,JI Jianfei.Noise characteristics and array gain of an acoustic vector-sensor array influenced by random array errors[J].Journal of Harbin Engineering University,2011,32(5):624-631.
[5]FELDMAN D D,GRIFFITHS L J.A projection approach for robust adaptive beamforming[J].IEEE Transactions on Signal processing,1994,42(4):867-876.
[6]LI J,STOICA P,WANG Z S.On robust Capon beamforming and diagonal loading[J].IEEE Transactions on Signal Processing,2003,51(7):1702-1715.
[7]ZHU LIANG YU,MENG H E.A robust minimum variance beamformer with new constraint on uncertainty of steering vector[J].Signal Processing,2006,86(9):2243-2254.
[8]SELEN Y,ABRAHAMSSON R,STOICA P.Automatic robust adaptive beamforming via ridge regression[J].Signal Processing,2008,88(1):33-49.
[9]JIAN L,LIN D,STOICA P.Fully automatic computation of diagonal loading levels for robust adaptive beamforming[J].IEEE Trans on Aerospace and Electronic System,2010,46(1):449-458.
[10]GU Y J,ZHU W P,SWAMY M N.Adaptive beamforming with joint robustness against covariance matrix uncertainty and signal steering vector mismatch[J].IET Electronics Letters,2010,46(1):86-88.
[11]鄢社锋,马远良.传感器阵列波束优化设计及应用[M].北京:科学出版社,2009:235-237.
[12]VACCARO R J,CHHETRI A.Matrix filter design for passive sonar interference suppression[J].Journal of the A-coustical Society of America,2004,115(6):3010-3020.
[13]STEPHEN B,LIEVEN V.Convex optimization[M].Cambridge:Cambridge University Press,2004:156-160.
Robust adaptive beamforming based on iterative optimization
WANG Yan,WU Wenfeng,FAN Zhan,LIANG Guolong
(Science and Technology on Underwater Acoustic Laboratory,Harbin Engineering University,Harbin 150001,China)
The performance of common robust adaptive beamforming degrades with the increasing degree of the signal steering vector error.To solve this problem,a robust adaptive beamforming algorithm was proposed on the basis of searching optimal signal steering vectors with an iterative strategy.The objective function that maximizes the beamformer output power was constructed by a corrected steering vector,while the constraint was deduced from both respects of interference suppression and noise suppression.The approach of structuring constraint by using a matrix filter was given and the rationality was explicated.Considering the difficulty in solving the optimization problem,an iterative optimization method was proposed,and the method solved a second-order program problem at each iteration.The simulation results show that,compared with common methods,this proposed method achieves higher signal-to-interference-plus-noise ratios(SINR)in the case of a steering vector mismatch.Moreover,the prior information of this proposed method is easier to extract.
robust adaptive beamforming;matrix filter;iterative optimization;second-order program;steering vector
10.3969/j.issn.1006-7043.201306015
http://www.cnki.net/kcms/doi/10.3969/j.issn.1006-7043.201306015.html
TB566
A
1006-7043(2014)06-0741-06
2013-06-03.网络出版时间:2014-05-14 15:50:57.
国家自然科学基金资助项目(51279043,61201411,51209059);黑龙江普通高等学校青年学术骨干支持计划(1253G019);水声技术国家重点实验室基金资助项目(9140C200203110C2003).
王燕(1973-),女,教授,博士生导师;范展(1983-),男,博士研究生;
范展,E-mail:wwf@hrbeu.edu.cn.

