水面舰船风浪环境适应性模糊综合评价方法

焦甲龙，孙树政，任慧龙

（哈尔滨工程大学船舶工程学院，黑龙江哈尔滨150001）

水面舰船风浪环境适应性模糊综合评价方法

焦甲龙，孙树政，任慧龙

（哈尔滨工程大学船舶工程学院，黑龙江哈尔滨150001）

为了研究舰船实际航行中的综合性能，综合船舶原理的多个学科对水面舰船风浪环境适应性提出一套全面的评价指标，采用层次分析法和熵值法的主客观综合方法得到各指标权重，并采用模糊综合评价模型作出最终评价。综合评价过程中通过选用半岭型函数将数据转化为百分制和选用正态分布函数确定隶属度使得评价结果更加合理。通过以某船型优化为算例的风浪环境适应性综合评价结果表明该评价方法具有一定的应用价值。

水面舰船；模糊综合评价；环境适应性；熵值；层次分析法；隶属度；正态分布

水面舰船风浪环境适应性是指舰船在所遭遇的风、浪、流、海水温度、盐度等一切外界条件的作用下，不仅能够被动地保持其原有的各种功能、性能不被破坏，甚至可以主动利用环境的改变以提高自身各方面的功能、性能［1］。其研究范围包括快速性、耐波性、操纵性、隐身性、波浪载荷、振动、稳性和抗沉性等多学科，其不仅仅是这些领域的简单叠加而是需要考虑各学科之间的矛盾性和一致性等综合因素，是一个多目标多变量的复杂系统。英法美日等国虽然对于研发高风浪环境适应性的舰船已取得明显成效，但是舰船风浪环境适应性的评价体系还不够完善。国内对舰船环境适应性评价方法的研究更是处于起步阶段，还有许多工作需要开展和完善。徐昌文［2］将模糊数学理论应用于船舶工程中。赵峰等［3］曾提出过基于系统工程思想的MDO方法研究舰船在风浪中的综合航行性能。孙树政［4］曾提出过专家评分法和层次分析法等模型评价船舶环境适应性。

一套完善的评价指标体系包括3个方面：全面合理的评价指标、科学的指标权重和完善的评价方法。本文综合现有的研究状况分别从这3方面逐项着手建立出一套更加完善的评价体系。本文综合多学科对水面舰船风浪环境适应性建立出一套全面的综合评价指标；采用主客观结合的综合评价方法，将层次分析法和熵值法相结合对指标进行赋权；运用多级模糊综合评价模型对舰船环境适应性作出最终评价。

1 多级模糊综合评价模型

多级模糊综合评价［2］是对许多综合问题进行评价的一种有效方法，在很多工程领域均有广泛的应用。评价的原则是首先在较低层次中进行一级综合评价，在此评价的基础上，再进行较高层次的二级综合评价，这种多级模糊综合评价方法与人脑处理复杂问题的思维方式十分相似。

1.1 建立因素集

设因素集为

式中：元素ui（i＝1，2，..，n）是第1层次中的第i个因素，它由第2层次中的m个子因素决定，即

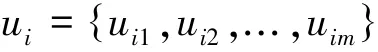
式中：元素uij（i＝1，2，..，n；j＝1，2，..，m）是第i个因素的第j个子因素。

要对水面舰船风浪环境适应性做出科学合理的评价必须要建立科学合理的评价指标体系，本文综合多学科对水面舰船风浪环境适应性建立出一套全面的综合评价指标，如表1所示。

表1 环境适应性评价指标Table 1 Evaluation indexes of environmental adaptability

1.2 建立权重集

根据每一层次中各个因素的重要程度，分别对每一因素给出相应的权数，于是得到各个层次的因素权重集。第1层次的因素权重集：

式中：元素ai（i＝1，2，..，n）是第1层次中第i个因素ui的权数；第2层次的因素权重集：

式中：元素aij（i＝1，2，..，n；j＝1，2，..，m）是第2层次中第i个因素的第j个子因素uij的权数。

因素权重的确定是综合评价过程中的一个重要环节，指标权重的确定是否科学、合理、准确，将直接影响最终评价结果的准确性。本文采用主客观结合的方法，将层次分析法和熵值法相结合对指标进行赋权。

1.2.1 层次分析赋权法

层次分析法（AHP）是一种处理多目标、多层次问题的有效方法，通过咨询专家两两比较指标的重要程度，从而得到指标权重，具体步骤如下：

1）比较指标之间的相对重要程度，并按照同样重要、稍微重要、相当重要、强烈重要、极端重要5个等级分别以1、3、5、7、9对指标间的相对重要程度进行标度。

2）根据指标之间的两两相对重要程度构造判断矩阵，求出最大特征根及其所对应的特征向量。

1.2.2 熵值赋权法

设待评价的舰船数目为t，m项评价指标组成的数据矩阵为X＝［xij］tm，对于某项指标，若各待评对象的指标值xij间的差距越大，则该指标在综合评价中所起的作用就越大；反之，作用越小［7-9］。在指标数据矩阵中，某项指标值差异程度越大，信息熵越小，则该指标的权重越大；反之，某项指标值的差异程度越小，信息熵越大，则该指标的权重越小。

熵值赋权用于对第1层次中第i（i＝1，2，..，n）个因素集的m个子因素赋权。熵值赋权法的步骤如下：

1）计算因素对指标的贡献总量Ej：

2）定义Dj为第j个指标下各方案贡献度的一致性程度：

3）计算各指标属性的权重aij：

1.2.3 组合权重的确定

设由层次分析法和熵值法确定的第1层中第i（i＝1，2，..，n）个因素集的m个子因素权重向量分

定义组合权重向量Ai和偏好系数β，则指标组合权重，取偏好系数β＝0.5。

以上确定的是第2层次中各因素的组合权重，第1层次中各因素的权重由层次分析法所得结果确定。

1.3 建立备择集

备择集是对评判对象可能做出的评判结果所组成的集合，因而无论因素层次有多少，备择集都可以只有一个，表示为

式中：元素vk（k＝1，2，..，p）是可能作出的第k个评判结果。

1.4 一级模糊综合评价

由于每个因素都是由低一层次的若干子因素决定，因而对于每一因素的单因素评判，可以看成是低一层次的多因素综合评判。显然，一级模糊综合评判即是相对于第2层次的多因素综合评判。设对评判对象考虑第2层次子因素uij作出评判结果vk的隶属度为

rijk（i＝1，2，…，n；j＝1，2，…，m；k＝1，2，…，p）则第2层次的评判矩阵可表示为

式中：第j行表示考虑第2层次第j个子因素uij的单因素评判集。于是，一级模糊综合评价集为

1.5 二级模糊综合评价

在考虑2个因素层次的情况下，二级模糊综合评价即是对于第1层次所有因素ui（i＝1，2，…，n）的综合评判。可见一级模糊综合评价集Bi也就是二级模糊综合评判的评判矩阵R，即

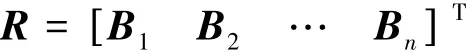
于是，二级模糊综合评判集为

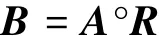
1.6 模糊综合评价过程

将评价原始数据转化为百分制为模糊评价进行数据预处理。各种模糊综合评价模型都能在特定的运算下得到不同的评价结果，因此确定隶属函数和综合评价模型至关重要。

1.6.1 数据的预处理

通过试验或理论的方法可以得到某评价指标的评价数据，并给出该指标的衡准范围，将评价数据与该指标的衡准范围相对比作为计算所采用数据的量度。如果某个指标远大于或远小于衡准值，则会使该指标的权重过度夸大或缩小，为了消除数据失真采用半岭型函数［10］作为转换函数将评价数据转化为百分制评分数据：

式中：N为百分制得分，umax为指标的最大值，umin为指标的最小值，u为该指标的数值。k＝0时指标数值越大环境适应性越好，k＝1时指标数值越小环境适应性越好。

图1 半岭型函数图形Fig.1 Graph of half-ridge like function

由于M（·，+）模型最充分考虑到各种因素的影响和全面反映各单因素评判的信息，因而在工程模糊分析中常采用这一模型，本文也采用这一模型进行计算。

2 算例分析

半岭型函数在指标值较大或较小时变化较平缓，而在中间值时变化较大，这与自然界的客观现象的规律相符，并且也非常符合人类的惯常评价思维。1.6.2 确定隶属度

在模糊数学中对于一个元素是否属于某一子集不是绝对地肯定或否定，而是把对该子集的属于程度用隶属度的概念加以描述。

通过分析建立指标得分N相对于各备择元素的隶属度函数，采用具有正态分布特性的模糊分布

本文以某万吨级高速圆舭船（R0）为参照船型，分别设计出深V船型方案（V1和V2）以及UV过度船型方案（UV1和UV2）作为目标优化船型，以研发高风浪环境适应性新船型。各船型横剖线图如图2所示，各船型主尺度如表2所示。现对5个舰船方案在七级海况（h1／3＝7.5 m）下以航速30 kn迎浪航行时的风浪环境适应性进行模糊综合评价。

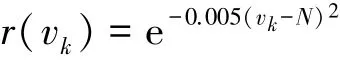
计算某指标得分对备择集中各分数等级的隶属度。式中：r（vk）为隶属函数，vk为备择集中的元素分数等级，N为该指标的百分制得分。

1.6.3 模糊综合评判模型

在不同的问题中，选取不同的模糊综合评判模型造成的信息得失会对评价结果造成很大的影响，常用的模糊综合评判模型归纳如下：

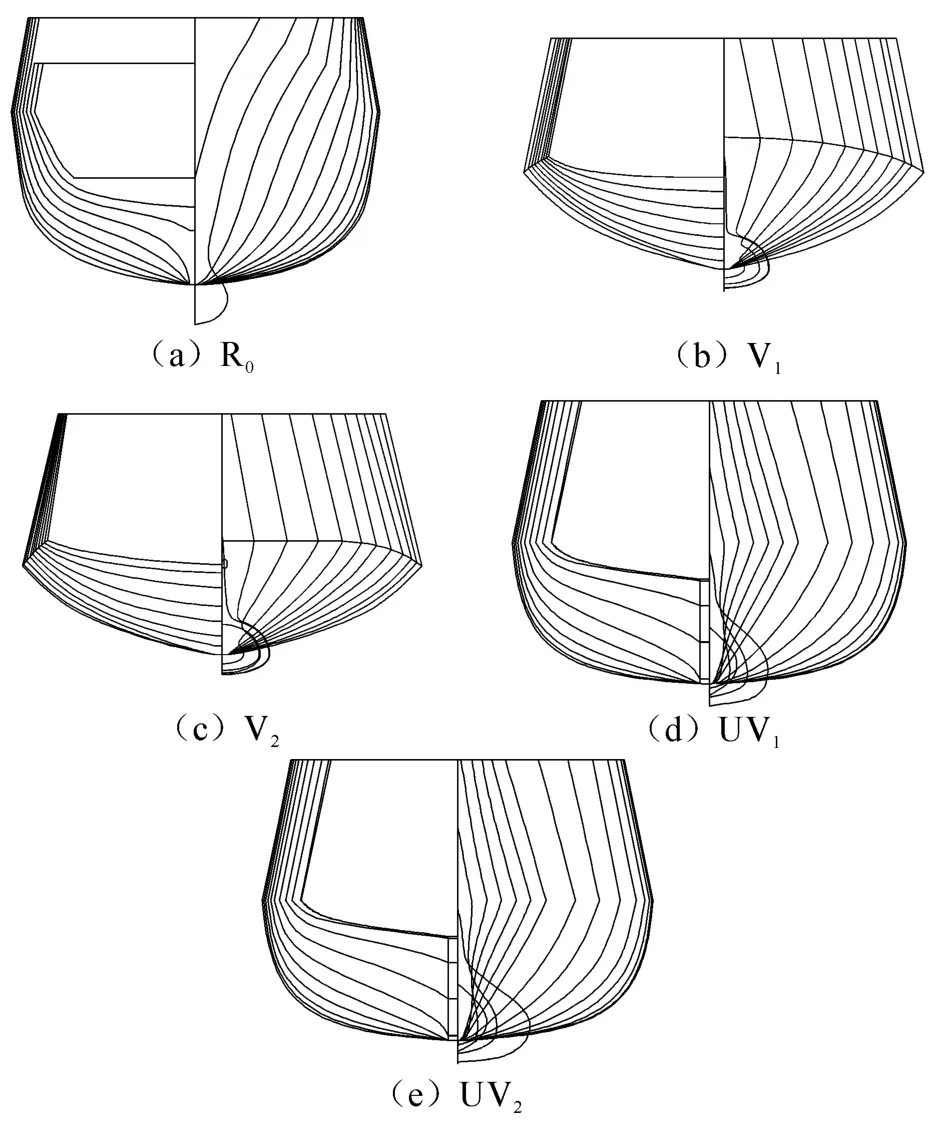
图2 各船型横剖线图Fig.2 Body plans of each ship

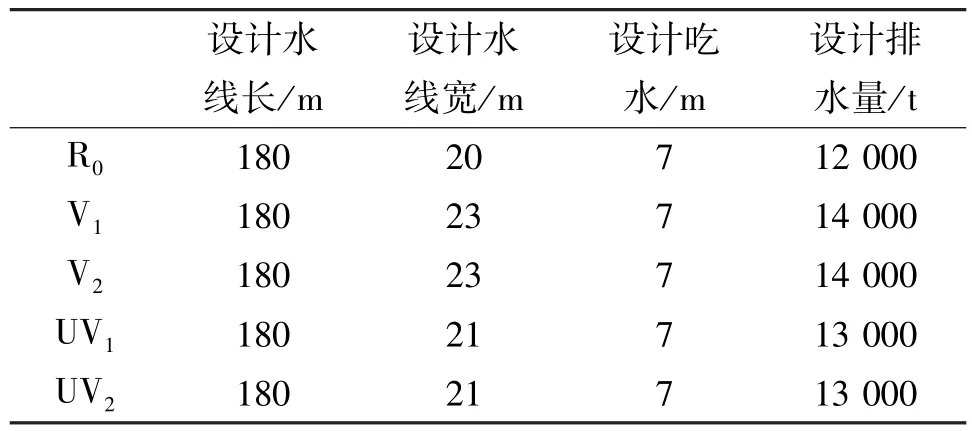
表2 各船型主尺度Table 2 Principal dimensions of each ship

2.1 评价指标的建立

考虑到模型试验和理论计算所得数据的有限性，本文只选取了一些典型的指标，计算或测量指标的数据值。其中耐波性和快速性指标数据由水池模型不规则波试验得到，模型缩尺比为1∶50，所给出的指标数据均为换算成实船后的数据，升沉、纵摇和加速度均为统计的1／10最大值。稳性数据通过参考经验公式计算得到，其中抗横风速为舰船在静水当中的计算数值，稳性衡准数为舰船在飓风作用下的数值。为了充分体现分数差，最小值和最大值即分别取自现有的数据值，典型指标的选取以及数据如表3所示。2.2 指标权重的确定

表3 典型指标选取及数据Table 3 The data of typical indexes

层次分析法中，第1层次的判断矩阵为

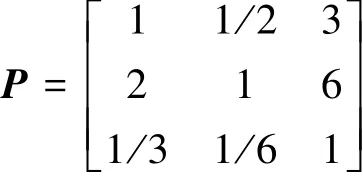
第2层次的判断矩阵为

以上判断矩阵通过咨询专家的方式得到。

熵值赋权法中，根据表3和表5的客观数据信息计算权重。

第1层次的指标权重由层次分析法所得结果来确定，A＝［0.3 0.6 0.1］。

第2层次的指标权重根据层次分析赋权法和熵值赋权法的组合来确定，其结果如表4所示。

表4 组合权重确定Table 4 Determination of the combination weights

2.3 建立备择集

为评分简洁清晰起见，以百分制的评分方式给出V＝｛10，20，30，40，50，60，70，80，90，100｝，共10个等级，所有指标均选定此备择集。

2.4 评价过程

通过半岭型函数将表3数据转化为百分制得分，结果如表5所示。

以R0船型为例，将百分制得分代入隶属函数以确定某指标得分对备择集中各分数等级的隶属度，然后将隶属度归一化即可得到模糊评判矩阵：

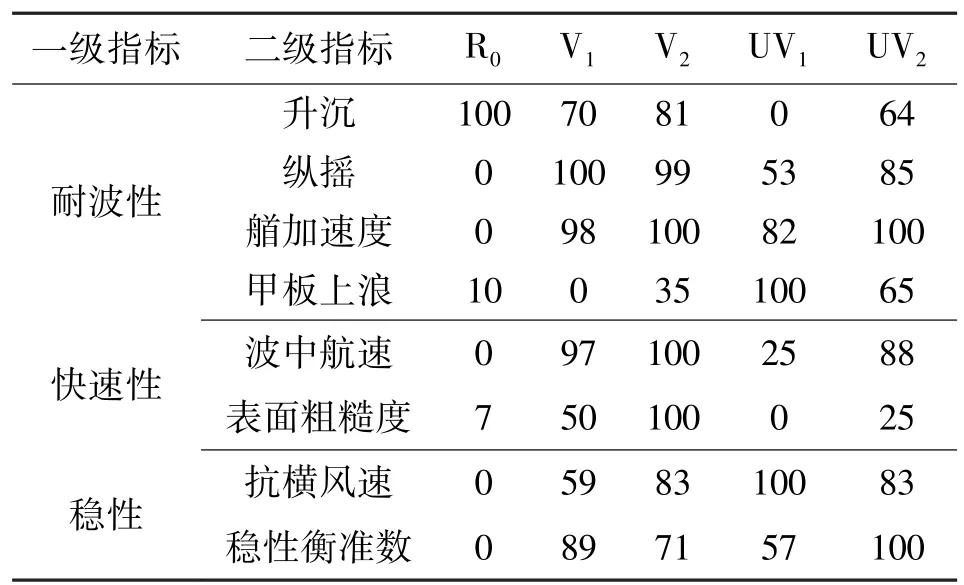
表5 评价数据百分制得分Table 5 Evaluation data of percentile

得到隶属度之后就可以进行模糊计算，本文选用M（·，+）模型计算，得到圆舭船型的一级和二级模糊综合评价集如表6所示。其他船型的计算过程与此相同。

将二级模糊综合评判集与备择集相乘即可得到评价结果：

此评价结果即为不同方案的最终百分制得分，根据此结果可以对优化方案进行筛选，舍弃分数较低的方案，而保留分数高的方案，该结果具有形式简单等优点。

表6 圆舭船模糊综合评判集Table 6 Fuzzy comprehensive evaluation sets of round bilge model

2.5 评价结果

5个船型的百分制综合评价结果如表7所示。

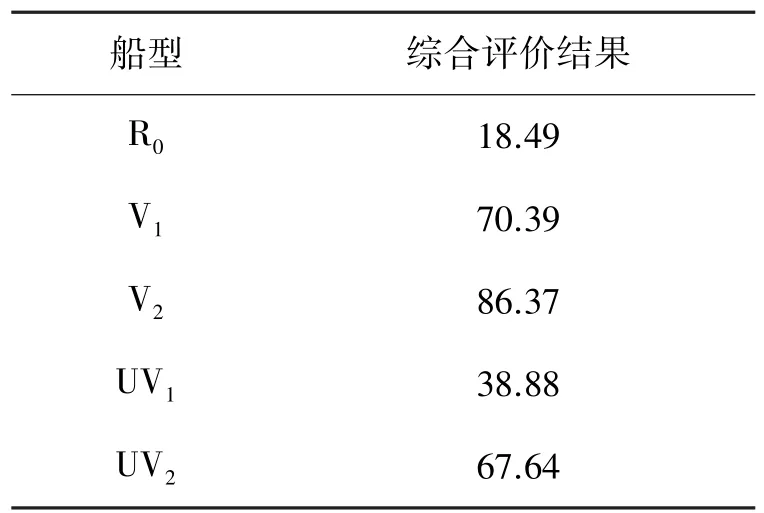
表7 各船型评价结果Table 7 Evaluation results of each ship

评价结果表明V2船型的得分最高，R0船型得分最低，所设计船型的风浪环境适应性均有所提高。评价结果以分数的形式给出一目了然，且分数差值明显，评判中会出现得分很低的船型，在船型优选时可以直接剔除。

3 结论

本文应用多级模糊综合评价模型建立出一套水面舰船风浪环境适应性评价指标体系，并以某船型优化为算例进行模糊综合评价，可以得出以下结论：

1）本文所建立的评价指标对于舰船在实际海浪中的综合航行性能具有典型的代表性；

2）主客观相结合的指标赋权方法更具有合理性；

3）评价结果以单一分数表达具有直观方便的特点，且与实际情况相符合。该评价系统在船型方案优选、船级评定等方面具有较高的参考应用价值与广泛的应用前景。

［1］李积德.船舶耐波性［M］.哈尔滨：哈尔滨工程大学出版社，1992：65-72.

［2］徐昌文.模糊数学在船舶工程中的应用［M］.北京：国防工业出版社，1992：122-131.

［3］赵峰，程素斌，杨磊，等.水面舰船航行性能MDO系统顶层设计研究［J］.船舶力学，2012，16（11）：1257-1266.ZHAO Feng，CHENG Subin，YANG Lei，et al.Top-down design research for the navigational performance MDO system of naval surface combatant［J］.Journal of Ship Mechanics，2012，16（11）：1257-1266.

［4］孙树政.高耐波性单体复合船型环境适应性评估［D］.无锡：中国船舶科学研究中心，2013：66-73.SUN Shuzheng.Evaluation of environment adaptability for hybrid monohull with high seakeeping performance［D］.Wuxi：China Ship Scientific Research Center，2013：66-73.

［5］武月琴，傅耘，敖亮.典型环境条件下装备环境适应性的评估方法［J］.装备环境工程，2010，7（6）：109-112.WU Yueqin，FU Yun，AO Liang.Equipment environmental worthiness evaluation method in representative environmental condition［J］.Equipment Environmental Engineering，2010，7（6）：109-112.

［6］熊德国，鲜学福.模糊综合评价方法的改进［J］.重庆大学学报，2003，26（6）：93-95. XIONG Deguo，XIAN Xuefu.Improvement of fuzzy comprehensive evaluation method［J］.Journal of Chongqing University，2003，26（6）：93-95.

［7］林望，王义闹.研发人员绩效的熵值模糊综合评价模型［J］.温州大学学报，2008，29（4）：1-5.LIN Wang，WANG Yinao.Model for the fuzzy assessment of entropy power of research and development personnel performance［J］.Journal of Wenzhou University，2008，29（4）：1-5.

［8］丛建春，杨玉中.基于熵权的模糊综合评价模型的库存控制绩效评价［J］.价值工程，2009（10）：78-81.CONG Jianchun，YANG Yuzhong.The evaluating on performance of inventory controlling based on entropy-weighted fuzzy comprehensive evaluation model［J］.Value Engineering，2009（10）：78-81.

［9］刘力，周建中，杨俊杰，等.基于信息熵的改进模糊综合评价方法［J］.计算机工程，2009，35（18）：4-6.LIU Li，ZHOU Jianzhong，YANG Junjie，et al.Improved fuzzy comprehensive assessment method based on information entropy［J］.Computer Engineering，2009，35（18）：4-6.

［10］王海英，张正宇，吴赞敏.薄型织物手感的模糊评价［J］.纺织科技进展，2008（1）：58-60.WANG Haiying，ZHANG Zhengyu，WU Zanming.Fuzzy evaluation of the lightweight fabric’s handle［J］.Progress in Textile Science and Technology，2008（1）：58-60.

A method of fuzzy comprehensive evaluation of the adaptability of surface ships in stormy wave environments

JIAO Jialong，SUN Shuzheng，REN Huilong
（College of Shipbuilding Engineering，Harbin Engineering University，Harbin 150001，China）

：In order to study the integrative performance of a ship in actual navigation，a set of overall evaluation indices of the adaptability of the ship in stormy wave environments were proposed by integrating a multidisciplinary ship theory.The analytical hierarchy process and entropy were used to obtain the index weights.Then the final evaluation was made by using the fuzzy comprehensive evaluation model.The data were converted into percentiles by use of the half-ridge-like function and the membership degree was determined by use of the normal distribution function，which made the evaluation results more reasonable.Finally，an example of evaluating the adaptability of ships in stormy wave environments indicates that this method has a certain application value.

surface ships；fuzzy comprehensive evaluation；environmental adaptability；entropy；analytical hierarchy process（AHP）；membership degree；normal distribution

10.3969／j.issn.1006-7043.201306037

http：／／www.cnki.net／kcms／doi／10.3969／j.issn.1006-7043.201306037.html

U662.3

A

1006-7043（2014）06-0667-07

2013-06-19.网络出版时间：2014-05-14 15：49：25.

国家自然科学基金资助项目（51209054）；中央高校基本科研业务费专项基金资助项目（HEUCFR1201）.

焦甲龙（1990-），男，博士研究生；任慧龙（1965-），男，教授，博士生导师.

焦甲龙，E-mail：jjlship＠163.com.