学生发展性学习评价模型的理论建构

邹敏 谭顶良

学生发展性学习评价模型的理论建构

邹敏 谭顶良

传统以学生的学习成绩为主要产出指标的评价方式与教育目标存在着偏差，严重影响了学生的发展，受到了很多批判。随着评价理论的发展与现实问题的凸显，应新课改所提出的发展性评价要求，本研究试图就学习评价的发展性功能探讨学生学习效率的评价模型。

发展性评价；学习评价；模型

一、问题提出

由于我国长期以来对学生的学习评价较少关注学习起点以及投入因素的影响，埋没了学生的主观努力与实际的进步幅度，导致我国教育中的“片面追求升学率”和“高分低能”、学生的学习时间投入与产出不相匹配的现象。随着对素质教育认识的不断深化与新课改具体目标的设置，新型的学习评价除了关注全面性与过程性评价外，更重要的是，逐渐关注学生的发展性评价。

依据新课改的要求，发展性评价要根据学生的个别差异来评价其进步幅度，即评价学生学习的有效性。因为学习基础差、成绩并不优秀的学生未必学习效率就低，而学习基础好、成绩优秀的学生未必学习效率就高，因而评价要考虑学生在原有学习基础上的发展。我们需要考虑的是：假如学生处于同样的学习起点，那么他们的学习差异会如何？要保证素质教育的真正实施，评价者就必须在学生原有水平的基础上对学习效率进行相对有效性评价。

新课改明确提出：要改变评价过分强调甄别与选拔的功能，发挥评价的教育功能，促进学生在原有水平上的发展。但现有的学习评价多是针对学生学习的比较性评价，虽然体现了前一阶段学习的结果，但未能提供学生后期阶段学习的反馈信息。正如有学者所指出的：当前学业评价中存在的一个主要问题就是缺乏对考评信息的深度挖掘，且未能体现考评的诊断与发展功能。

鉴于此，本研究试图就学习评价的发展性功能探讨学生学习效率的评价模型。

二、发展性学习评价模型的理论探讨

1.增值性评价

有关学生学习效率评价的数学模型在以往的研究中已有所体现，这种数学模型大多关注学习时间变量与学习结果之间的关系，即用数学表达的形式来描述二者之间的关系。已有学者指出了一种学习时间变量与学习结果的线性关系模型，并将这一线性相关模型表示为

其中，Lt表示经过时间t后学生的学习成绩水平；

L0表示学生初始的学习成绩水平；

K为常数。

这一模型最重要的假设就是学习时间与学习成绩之间呈线性关系，且学生每时每刻的学习效率完全相同。这显然不符合学生的学习实际，因为学生的学习活动较为复杂，不同时刻的学习效率均是不同的，即使学生对同一内容花费相同的学习时间，其学习成绩也未必相同。基于此，卡韦特提出了学习时间与学习结果的动态关系数学模型

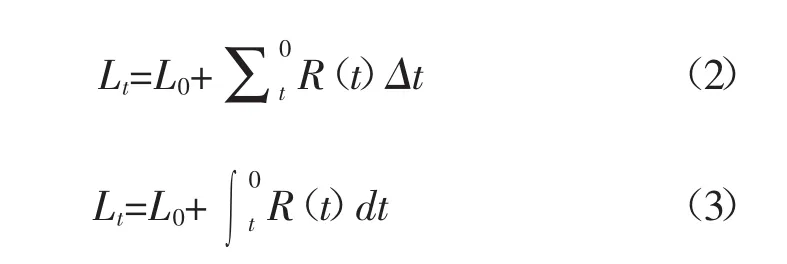
研究者指出：如果学生的学习效率R（t）比较稳定，那么经过时间Δt后的学习成绩可表示为式（2）；如果学生学习效率R（t）不稳定，那么一定时间后的学习成绩应以各个时刻学习成绩积分的形式来表示，可表示为式（3）。

以上三式均隐含着一种认识，即学生经过一段时间后的学习水平是由原有的成绩基础和新增长的水平两部分构成，其中新增长的水平是学习效率与学习时间的函数。这一表达形式固然为学习效率评价提供了新的视角，但其中也忽视了一项因素——学生的初始成绩水平并非是固定不变的，而是在后期的学习过程中不断变化的，或遗忘，或保持，或增值。比如说，学生A、B初始成绩均为80分，经过一段时间新知识的学习后成绩亦均为80分，但学生A在学习中将原有知识遗忘了10%，学生B在学习中原有知识水平保持不变。据此可知，学生A知识的增值要高于学生B，但依据式（2）（3）可得，学生A、B知识的增值水平相等。可见，简单地将学习后的水平扣除初始的水平不能完全表现出学生知识水平增值的部分。

卡韦特提出的学习时间与学习结果的动态关系数学模型为学习效率评价的研究提供了一种理念，即学习效率评价亦应针对每位学生的发展进行增值性评判，而不仅仅关注于将不同学生的学习效率进行相互比较。通常认识中，效率水平是指产出与投入的比值，在此我们只考虑一种简单的产出投入模型，即将学生学习后的水平作为产出，将学生原有的水平作为投入，则指标的产出投入比具体可表示为

其中，ei表示学习后指标i的产出投入比；

yi表示学习后指标i的得分；

xi表示学习前指标i的得分；

ai表示学习后指标i测试内容较之学习前指标i测试内容的增值系数，采用专家赋值的方式较为合理。

采用式（4）对学生的产出投入比进行评价基于以下两大原因。

一是由于通常情况下，后期的学习内容是以前期的学习内容为基础的，学习内容的获得是逐渐呈递增趋势的，即后期的学习内容较之前期的学习内容，其获取均有所增加，因而在这一模型中我们加入了增值系数，表示学习内容在原有学习基础上的增长比率，据此将后期的测试得分加以调整，从而更为合理地表示学生学习的产出投入比。

二是因为评价应真切地体现学生水平的增长，使得学生用努力换来的所得均能够得以充分展现，而不宜抹杀他们在学习过程中的努力程度。若采用卡韦特提出的学习评价数学模型，很多时候即便考虑了前后测试内容的增值系数，仍免不了会出现知识增长为负的情况。比如说，学生在前期测试中得了40分，经过一段时间新知识的学习后，后期的测试得了30分，但据评判，后期测试内容的增值系数为1.2，由此后期测试得分可调整为30×1.2=36分，由（3）式可得，新增长的水平为36-40=-4分，但事实上，该生的水平是提高了的，因为测试涉及到新的内容，若其中鲜少涉及先前知识的保持项目，那么这30分本身就可以看作是新知识的增长水平，因而不能简单地将后期得分减去前期得分来表现增长的部分。再者，负数本身就是对学生学习努力的一种抹杀，因而为了体现学生学习水平的增长，本研究采用产出投入比来评判学生的学习。

基于学生发展评价建构的n项指标，其总体产出投入比可表示为

其中，ki表示评价指标i占总指标的权重；

ai为专家评定的增值系数。

2.相对性评价

有关学生学习的效率评价既不能抹杀由学生自身努力所带来的水平增长，也无法忽视自身与他人比较时所增长的程度，有些学生虽然在学习过程中付出了努力，产出投入比较高，但这一阶段其他同龄学生的学习效率可能更高，因而，在学习评价过程中，既要考虑体现学生自身增长水平的产出投入比评价，也要关注对不同学生的学习效率进行相互比较性评价。

既然要在学习群体中比较不同学生的学习效率，那么就无可避免地要考虑到学习群体的平均指标。在建构学生学习效率的评价模型时，可将学生经过学习后距离平均指标的差距与学习前距离平均指标的差距相互比较，若二者差距为正数，则表明学习相对进步，正数越大，进步幅度越大；若二者差距为负数，则表明学习相对退步，负数越小，退步幅度越大。当然，后一阶段的测试指标仍然要考虑测试内容的难度，同时也要顾及到学生原有的基础水平，如式（6）所示。

其中，ei表示学习后指标i的学习效率；

yi表示学习后指标i的得分；

xi表示学习前指标i的得分；

Xi表示指标i的满分分值；

di表示学习后指标i测试内容与学习前指标i测试内容的难度系数之比。为了符合日常习惯，本研究所界定的难度系数越大，表明测试内容越难；难度系数越小，表明测试内容越容易。其取值方式如式（7）所示。

由于与他人比较的相对效率评价无需考虑学生水平的真实增长，而主要是评价不同学生之间学习的相对效率，因而可采用式（7）的方式对测试内容进行难度系数比的评判。虽然这一评判方式纳入了群体平均数的概念，所得难度系数比并非一定大于1，但其本身所具有的相互比较成分并不影响对不同学生学习效率的比较。

基于学生发展评价建构的n项指标，其总体相对学习效率评价可表示为

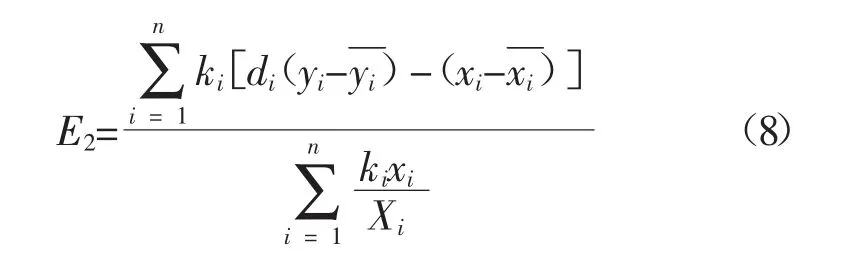
上述有关学生学习效率评价的（4）、（5）、（6）、（8）各式均是以学生学习时间的统一性为前提假设的，若考虑到学生用于不同指标的时间差异性，就应在模型中加入时间t这一因素，因为很多指标最终的产值在一定程度上是以时间投入的增加而增长的。据此，上四式可调整为以下变式

式（4）变式

式（5）变式

式（6）变式

式（8）变式

其中，ti表示平均每天用于指标的时间占全天24小时的比率。

综上所述，本研究所建构的学生学习效率评价模型主要从两个方面入手：一是关注学生学习的增值性评价，一是关注学生学习的相对效率。评价目的不同，评价的方式与系数的设置也有所区别，具体如表1所示。

表1 学生学习发展性评价模型整合

三、模型应用

为解释模型的可操作性，基于上述所建构的发展性学习评价模型，本文以四名中学生的数学测试成绩（采用单项指标）为例，运用增值性与相对性评价模型对其学习效率进行评价。

数据采用被试前后两次不同内容的数学测试成绩（以百分计）。结合任课教师的评定，这里暂设两次测试间被试所学知识的增值系数为1.5，具体情况如表2所示。

依据上式（4）可得四名学生的学习增值结果，即测试2成绩除以测试1成绩再乘以增值系数；上式（9）是在式（4）的基础上考虑学生的学习时间对学习效率所产生的影响，即纳入学生的学习时间计算其学习增值情况。

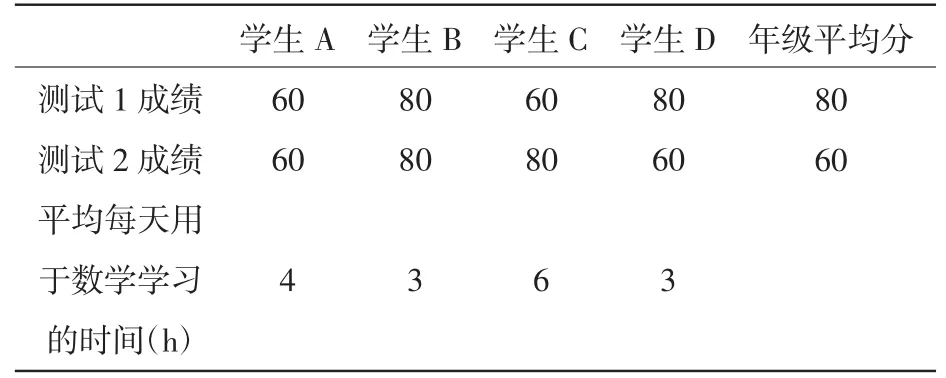
表2 四名中学生数学测试成绩基本情况

依据上式（7）可计算系数d=（100-60）/ （100-80）=2，将相应数据代入上式（6）可得学生单项数学指标的学习效率，上式（11）则是在式（6）的基础上考虑学生的学习时间对学习效率产生的影响。

所得结果如表3所示。

表3 四名中学生数学学习的评价结果

表3的学习效率评价结果中，增值性评价与相对性评价皆显示了两种情况下的被试学习效率：一是假设学生用于学业的时间大体相同，则省略学习时间这一变量来评价学生的学习效率；二是当考虑学生用于学业的时间各不相同时，则将学习时间这一变量纳入到学习效率评价当中。结果数据越大，表明学生的学习效率越高。表3显示，学习时间对学习效率的影响比较明显，学习时间越长，学习效率相对越低，当不考虑学习时间时，学生C的增值效率相对较高，但由于其用于数学学习的时间比其他同学要长，所以当纳入时间变量时，其学习效率降低。相对性评价的结果解释是以0为基准的，若评价结果约等于0，表明被试这一阶段的学习仍相对稳定；若评价结果小于0，则表明被试这一阶段的学习与被试的整体水平比较而言有所退步，数据越小，表明退步的幅度越大；若评价结果大于0，则表明被试这一阶段的学习与整体水平比较而言获得了进步，正向数据越大，表明进步的幅度越大。由表3我们可以看出，经过这一阶段的学习，A、B、C三名学生均有所进步，其中B、C进步的幅度较大，而D的数学学习对于整体水平而言较为稳定。增值效率相同的被试，其进步幅度不一定相同，如在不考虑学习时间的情况下，学生A、B学习的产出投入比相近，但与整体比较而言，其相对的学习效率却有高有低，可见增值效率与相对效率对于评价学生的学习具有不同的效用。

四、讨论

本研究关于学生学习效率的评价模型主要关注学生学习的发展性评价，包括增值性评价与相对性评价，有助于学生在学习过程中进行自我比较与他人比较，从而凸显出评价的重要价值。

增值性评价与相对性评价最重要的区别就在于，增值性评价采用产出投入比，用于体现学生基于自身水平上真实的水平增长，即根据学生的个别差异来评价其进步幅度，突出了学生自身的纵向发展；相对性评价则主要采用相互比较的方式，用于体现不同学生之间的效率差异，即根据学生与整体之间的差异来评价其进步幅度，突出了学生之间的横向比较。二者所采用的系数具有不同的含义，增值性评价的系数a主要是为评价学生水平增值程度而设置的，若采用d对测试内容的增值进行评判，就又引入了学生之间相互比较的成分。因为有时候会出现测试内容实际增值，但学生水平增长程度普遍较高的现象，此时若采用d评判测试内容的增值程度，那么就会抹杀学生学习过程努力的幅度，因而应用产出投入比进行增值性评价时，对系数的确定采用专家赋值的方式较为合理；而相对性评价的系数主要是为评价不同学生之间相互效率高低而设置的，进行难度系数评判并不影响不同学生学习效率的比较。为了将二者加以区分，我们把增值性评价中的系数a称为增值系数，将相对性评价中的系数d称为难度系数。将增值性评价与相对性评价结合起来评价学生的学习效率不仅可以体现出学生真切的纵向学习增长，发挥评价的教育功能，而且可以使学生通过相互之间的横向比较来了解自身的学习效率，从而为进一步发展指引方向。

学生学习发展性评价是基于学生原有基础的一种评价理念，本研究所建构的增值性评价与相对性评价模型皆是此理念的一种表达。增值性是基于原有基础上的一种实际的增长，而相对性则是基于原有基础与所在群体水平的一种相对进步幅度变化，两种评价的目的不同，所得结果也不一。若要对学生自身的发展进行纵向评价，那么适于采用产出投入比的增值性评价；若要对学生相互之间的学习效率进行横向比较，则适于采用相对性评价。

需要指出的是，考评更重要的价值在于诊断，学生的学习过程与结果中包含着丰富的信息，充分挖掘这些信息对学生的发展至关重要。在评价学生学习效率的同时，若忽视其诊断功能，那么就无法寻求学习低效的原因。若学生通过评价都无法获知自己今后的努力方向，那么可见评价的价值并不大。在有关学习评价的模型中，运筹学当中的数据包络分析方法无疑对学生的学习诊断具有重要的价值。

［1］辛涛.新课程背景下的学业评价：测量理论的价值［J］.北京师范大学学报，2006（1）：56～61.

［2］白益民.学习时间与学习结果关系模型研究述评［J］.外国教育研究，1999（6）：1～7.

［3］刘亚荣.我国高等学校办学效率评价分析［J］.教育与经济，2001（4）：31～36.

［4］陈通，白建英.西部地区高等教育投入产出相对有效性的评价研究［J］.西北农林科技大学学报，2003，3 （2）：102～105.

［5］郭新立.基于DEA的学科有效性评价［J］.中国管理科学，2003，11（6）：78～81.

［6］窦爱女.教师教学效益的DEA评价［J］.培训与研究——湖北教育学院学报，2003，20（2）：66～67.

［7］贾微.网络课程教育综合效益评价研究［D］.大连：大连理工大学，2006.

［8］程利军.评价学习成绩相对有效性的数学模型［J］.滨州师专学报，1999，15（4）：27～29.

［9］王香柯，王金柱.基于数据包络分析模型的学习效率评价研究［J］.陕西教育学院学报，2002（1）：66～68.

责任编辑/王彩霞

G40-058.1

A

1674-1536（2014）10-0004-05

本文为全国教育科学“十一五”规划项目“中小学生课堂学习投入产出比研究”（课题批号：DEA060138）阶段性成果。

邹 敏/潍坊医学院心理学系教师，博士，主要从事学习与教学心理研究。（潍坊 261053）

谭顶良/南京师范大学心理学院教授，博士生导师，主要从事学习与教学心理研究。