有限导流压裂定向井耦合流动模型

贾 品， 程林松， 黄世军， 方思东

（中国石油大学（北京）石油工程学院，北京 102249）

有限导流压裂定向井耦合流动模型

贾 品， 程林松， 黄世军， 方思东

（中国石油大学（北京）石油工程学院，北京 102249）

考虑人工裂缝、斜井筒和地层中的耦合流动，将压裂定向井的流动分为地层向裂缝渗流、裂缝内流动和斜井筒变质量管流.采用镜像反映和势叠加原理，建立地层中势分布和渗流数学模型.应用边值理论，将人工裂缝面离散为裂缝网格，并与斜井筒变质量管流模型进行耦合，建立有限导流压裂定向井耦合流动数学模型，并形成相应的迭代算法.应用分析表明：该模型与Prats图版法相比，对于垂直缝吻合度较高；裂缝导流能力和井斜角对产量及裂缝面压力分布影响较大.

压裂定向井；有限导流；耦合模型；网格离散；产能

0 引言

随着滩海低渗透油田的大规模开发，为节约钻井成本，钻井平台大多建在陆地上.开发此类油藏普遍采用定向井，为获得较高产量，定向井通常进行压裂［1－3］.压裂定向井对于开发滩海油藏、多层系油藏和钻井平台不易建设的油田尤其有效.因此，研究压裂定向井的产能亟待进行.从研究现状看，国内外学者［4－6］只有对压裂定向井的压力动态做过研究，对裂缝有限导流时的产能研究几乎为空白.

基于前人对无限导流压裂定向井压力动态的研究［4－5］，将流动分为油层向裂缝渗流，裂缝内流动和井筒变质量管流.利用叠加原理、微源汇、边值理论和管流理论，同时考虑裂缝有限导流和井筒压力损耗，推导压裂定向井渗流耦合模型，建立压裂定向井的产能公式，可以预测压裂定向井的产能和压力分布.

1 压裂定向井及裂缝三维空间描述

将倾斜裂缝面离散为若干裂缝网格，并将井筒划分为若干井筒微元段.各裂缝网格有不同的网格压力和油层流量，各井筒微元有不同的流压和管流流量.

油层为上下封闭，均质等厚水平无限大油藏，油层厚度为h.假设定向井（见图1）沿X-Z平面，井斜角为θ，在油层中的长度为Ls，将其划分为M个微元段（见图2），每个井筒微元长度为ΔLs．压裂裂缝沿着Y方向延伸，纵向上完全穿透油层，裂缝半长为Lf，宽度为w，划分整个裂缝面为2N ×M个裂缝网格（见图3），裂缝网格沿裂缝延伸方向（Y方向）长度为ΔLf，沿井筒方向长度为ΔLs，与井筒微元长度一致.

设倾斜井筒上端点的坐标M0（x0，y0，z0），式1给出了井筒上第i微元段上任意一点坐标

图1 压裂定向井示意图Fig.1 Fractured deviated well

其中，1≤i≤M，t取值为0≤t≤1表示在第i微元段上的任意一点，例

图2 离散井筒示意图Fig.2 Discreted wellbore

图3 裂缝面网格示意图Fig.3 Fracture grid

如t＝0或t＝1表示第i微元段上的两个端点．由于井筒半径相对于裂缝半长很小，因此在计算裂缝面上任意一点坐标时，井筒半径可以忽略不计，则裂缝面上沿井筒方向第i网格，沿裂缝延伸方向第j网格上任意一点坐标

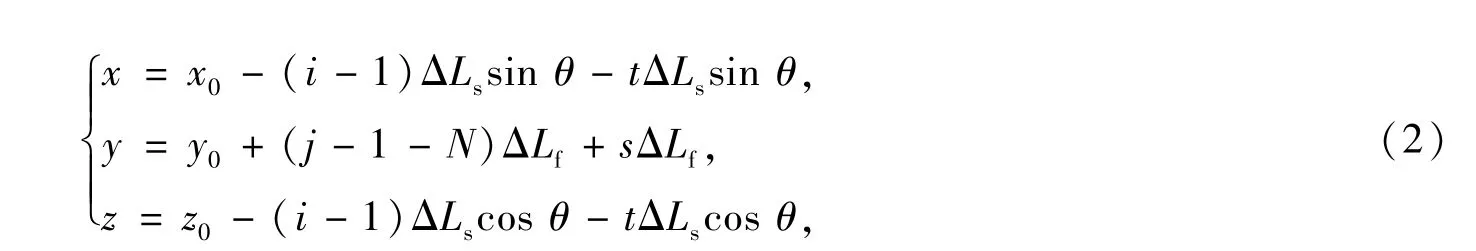
其中，1≤i≤M，1≤j≤2N；0≤t≤1，0≤s≤1表示在第（i，j）裂缝网格上X和Y方向上的任意一点.

2 耦合流动数学模型

2.1 油层向裂缝流动

根据刘想平［8］，黄世军［9］等人的研究，油层中任意一长为L，产量为Q的线汇在无限大油层M（x，y，z）点产生的势分布，将此结论引入到本文中．基于镜像反映原理，将上下封闭水平无限大油层中裂缝面的第（i，j）裂缝网格映射成无界地层中的倾斜板源，其z方向中点坐标Z为

其中zm，（i，j）为第（i，j）裂缝网格z方向的中点坐标.

设裂缝面的第（i，j）裂缝网格中与井筒平行的某条线汇（XZ平面上的线汇）y方向坐标为Y．利用叠加原理，可得该线汇在上下封闭油藏中M（x，y，z）点产生的势

等式中qr，（i，j）为油层到第（i，j）裂缝网格的流量，r1、r2分别为线汇的两个端点到M（x，y，z）的距离．εi，j定义为εi，j（Z，x，y，z；Y）＝ln［（r1＋r2＋ΔLs）／（r1＋r2－ΔLs）］．

对与井筒平行的线汇（XZ平面线汇）沿着裂缝延伸方向（Y轴正方向）积分，即对等式（3）的变量Y沿y方向积分，可得裂缝面的第（i，j）整个裂缝网格在上下封闭油层中M（x，y，z）点产生的势

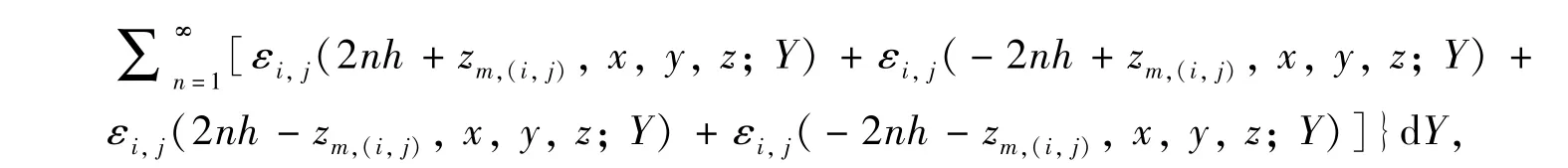
积分上下限为y2＝y0＋（j－N）ΔLf，y1＝y0＋（j－1－N）ΔLf．由于以上积分形式复杂，本文采用数值积分进行计算.

将整个裂缝面共划成了2N×M个裂缝网格．从左到右，从上到下依次对裂缝网格编号，序号为I＝j＋（i－1）2N．设供给边界处的势为Φe，则有

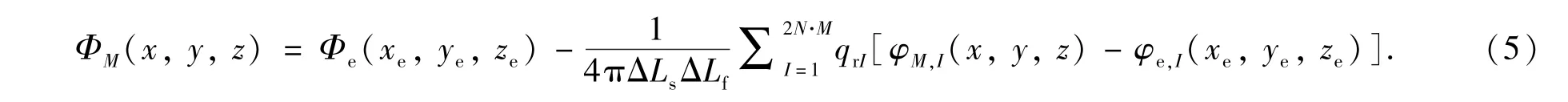
设供给边界处的压力为pe，第I裂缝网格的压力为pfI，油层流入第I裂缝网格的地层流量为qrI，则每个裂缝网格压力和油层流量的关系矩阵为

其中φi，j表示第J裂缝网格在第I裂缝网格中心处产生的势，φe，J表示第J裂缝网格在油层边界处产生的势，Km为基质渗透率，μ为流体粘度.由以上流动方程可以看出，给定裂缝网格压力，可以得到油层到裂缝网格的流量，反之可得到裂缝网格压力.

2.2 裂缝有限导流

裂缝面流动为稳态流动，即渗流过程为边值问题.以裂缝网格为研究对象，则流入流出该网格的流量包括两部分（见图4）：①相邻网格的流入流出流量；②油层到该网格的流量.

利用微元法对第（i，j）裂缝网格的控制方程进行推导．裂缝网格为均匀网格，i方向网格大小为Δx，j方向网格大小为Δy，油层流入裂缝网格的流量为qr，（i，j），裂缝宽度为w．根据物质平衡原理及达西渗流方程，以裂缝网格为微元，则有以下离散形式的控制方程

图4 裂缝网格流量示意图Fig.4 Scheme of flux to fracture grid

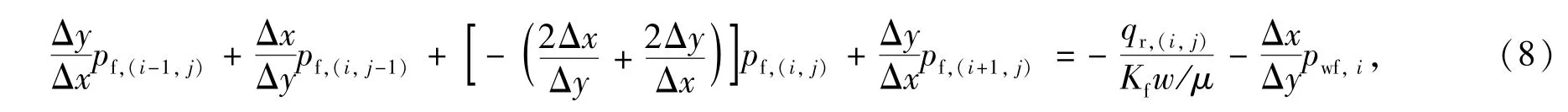
其中pf，（i，j）为第（i，j）裂缝网格压力，pwf，i为第i井筒微元流压，Kf·w为裂缝导流能力.

因此对于裂缝面流动，网格压力可由等式（7）和等式（8）计算.裂缝面共有2NM个网格，则共有2NM个流动方程，若给定油层到裂缝网格的流量qr，（i，j）（1≤i≤M，1≤j≤2N）和井筒微元压力pwf，i（1≤i≤M），通过求解2N×M个线性方程组，可以得到每个裂缝网格压力pf，（i，j）（1≤i≤M，1≤j≤2N）.

2.3 井筒变质量管流

压裂定向井的裂缝完全穿透油层时，油井生产过程中沿定向井井筒各处均有流体从裂缝流入井筒.从定向井底部到顶部，井筒内流体质量不断增加，井筒流动为变质量管流流动.国内外学者［10－12］对变质量流动做了大量研究，模型计算结果准确，且利用应用.引用于乐香等人［12］的结论，应用到压裂定向井微元井筒中（见图5），可以得到压裂定向井沿井筒的压力损失计算模型：

与井筒微元相邻的裂缝网格，控制方程为

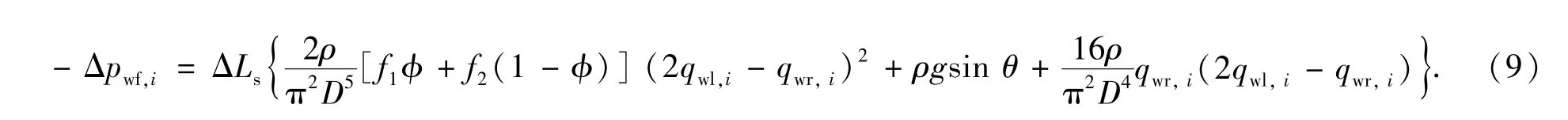
等式（9）右端第一项为摩擦阻力项，第二项为重力项，第三项为上下游端面压力项.其中，Δpwf，i为第i井筒微元与第i＋1井筒微元井底流压压差；φ为油层孔隙度；f1为生产井筒管壁摩擦系数；f2为由于从裂缝网格流入生产井筒的流体所造成的摩擦系数；qwl，i为第i井筒微元的管流流量；qwr，i为与第i井筒微元相邻裂缝网格流入该井筒微元的流量；ρ为流体密度；D为井筒直径，i的取值范围为1≤i≤M－1．

其中qwr，i可以由以下等式计算

图5 井筒微元及与其相邻裂缝网格示意图Fig.5 Wellbore grid and neighboring fracture grid

等式（10）右边第一项为与第i井筒微元左端邻的裂缝网格流入井筒微元的流量，第二项为与右端相邻的裂缝网格流入井筒微元的流量，i的取值范围为1≤i≤M．

3 耦合流动计算模型

若压裂定向井为定井底流压生产，则pwf，1为已知量，即油井生产时的定井底流压.假设计算出了裂缝网格压力和井筒微元压力，则由等式（10）和等式（11）可得出裂缝网格流入每个井筒微元的流量qwr和管流流量qwl．剩下未知量Δpwf，i和pwf，i共有2M－1个，联立等式（9）和等式（12）共有2M－2个方程，加上pwf，1为已知量，共有2M－1个方程组，则2M－1个未知量可以求解，pwf，i（2≤i≤M）可以计算出来.

生产井井筒微元管流流量qwl和井底流压pwf满足以下约束关系式

三部分流动模型有很强的耦合性，每一部分流动模型的计算都需要其他流动模型的计算结果.因此，为简化计算过程，并提高模型收敛性和计算效率，本文基于以下的耦合方法和迭代算法求解生产井产量和油层压力分布，对于矩阵方程，采用预处理共轭梯度法求解.具体计算流程图如下（见图6）.

具体耦合计算步骤如下

步骤1：井筒微元流压pwf，i（1≤i≤M）赋初值；

步骤2：裂缝网格压力pf，（i，j）（1≤i≤M，1≤j≤2N）赋初值；

步骤3：由等式（6）计算油层流入裂缝网格流量qr，（i，j）（1 ≤i≤M，1≤j≤2N）；

步骤4：由等式（7）和（8）计算裂缝网格压力pf，（i，j）（1≤i ≤M，1≤j≤2N）；

步骤5：判断步骤4计算的裂缝网格压力与步骤2的网格压力初值是否达到收敛条件.若收敛进行步骤6，否则返回步骤2；

步骤6：由等式（9）计算井筒微元流压pwf，i（1≤i≤M）；

图6 耦合计算流程图Fig.6 Flowchart of coupling calculation

步骤7：判断步骤6计算出的井筒微元流压与步骤1的井筒微元流压初值是否达到收敛条件.若收敛则计算结束，否则返回步骤1，继续计算，直到流压pwf，i收敛.

其中，步骤5和步骤7的收敛条件分别为以下形式：

步骤5收敛条件

4 应用分析

4.1 模型检验

为检验本文模型的准确性，根据我国东部某滩海油田压裂定向井的地层参数和完井数据（见表1），利用耦合流动模型进行计算，与Prats图版法［13］进行对比.Prats于1961年研究了压裂直井稳态渗流问题，给出了裂缝不同无因次导流能下的有效井筒半径，此方法只适用于计算垂直裂缝产能，而不能用来计算倾斜裂缝产能.因此为与Prats方法对比，设模型中的井斜角为0°.表1给出了主要计算参数，对比结果见图7.

表1 地层及完井参数Table 1 Reservoir and completeion parameters

从图7中可以看出，本文井筒无限导流时的产量与Prats图版法产量相差很小，井筒无限导流产量与Prats图版法产量几乎重合，吻合度较高.

4.2 裂缝导流能力的影响

裂缝为有限导流时，每个裂缝网格的压力Pf和油层到网格的流量qr不同.取压裂定向井井斜角为60°，不同裂缝半长，不同裂缝导流能力下的单井产量和裂缝面压力分布见图8.

油田现场压裂时，人工裂缝导流能力一般在300 mD·m～3 000 mD·m.从图8中可以看出，在此范围内产量随裂缝导流能力不断增加；当裂缝导流能力接近10 000 mD·m，产量不再由明显变化，裂缝接近无限导流.裂缝半长为120 m时，产量随着裂缝导流能力增加从12 m3·d－1增加到20 m3·d－1，说明裂缝导流能力对产量影响较大.

在不同裂缝半长下，裂缝导流能力的增加对单井产量的贡献不同.裂缝半长为200 m时，产量最大增加11 m3·d－1；而裂缝半长为40 m时，产量最大增加3 m3·d－1，因此在定向井压裂时，对于裂缝半长较大的生产井，增加裂缝导流能力对提高单井产能尤为重要.

图9为裂缝倾角60°，半长80 m，导流能力300 mD·m，裂缝面压力分布，图中纵坐标为生产井井筒方向，横坐标为裂缝延伸方向.

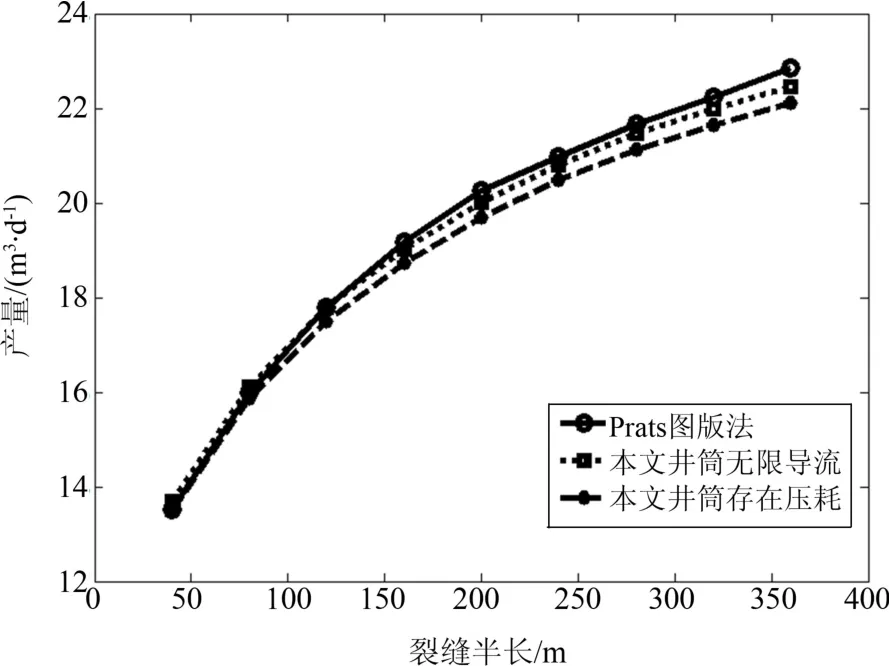
图7 本文模型与Prats图版法对比Fig.7 Results of coupled model and Prats method

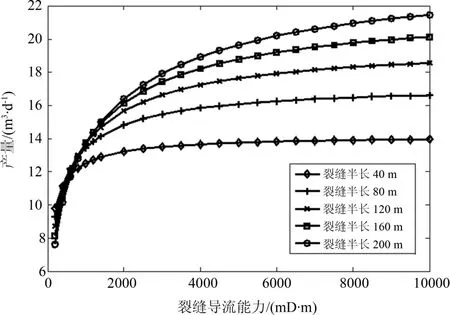
图8 不同裂缝半长不同裂缝导流能力下产量Fig.8 Productivity with different fracture length and conductivity

图9 裂缝面压力分布Fig.9 Fracture pressure distribution

根据图9，裂缝导流能力较低时，裂缝面沿横轴端部与井筒（横轴中间部位）压差较大，为2 MPa，井筒处上下两端也存在压差，最大为0.2 MPa，整个裂缝面压差较大.

4.3 井斜角和裂缝半长的影响

从图10可以得出，裂缝半长对压裂定向井的产能有较大影响，而当井斜角较大时，裂缝面与油层的接触面积增加，其对产能也有一定影响.因此，以下对井斜角和裂缝半长对产能的影响做以讨论.

裂缝导流能力为2 000 mD·m，井斜角为20°～80°，裂缝半长为40 m～200 m，不同裂缝半长和不同井斜角下的产量对比如下图.

从图10中不难得出，同一裂缝半长下，单井产量随着井斜角的增加而增大，当井斜角小于60°时，产量增加缓慢，井斜角大于60°时，产量增加很快，以裂缝半长40 m为例，井斜角小于60°时，产量增加1 m3·d－1，井斜角大于60°时，产量增加5 m3·d－1.井斜角增加，相同裂缝半长下，裂缝与油藏的接触面积不断增加，近井地带渗流阻力减小，产量增加.不同裂缝半长下，井斜角的增加对单井产量的贡献几乎相同.因此，在定向井开发油藏时，较大的井斜角可以显著提高生产井的产油能力.

图11中得到，井斜角一定时，裂缝半长越大，生产井产量越大，压裂定向井的产量与裂缝半长呈近似直线关系，说明由于裂缝半长增加而增大的等效井径与裂缝半长为指数关系.同样，不同井斜角下裂缝半长的增加对生产井的产量贡献几乎相同.

图10 不同井斜角下产量Fig.10 Productivity with different inclined angle

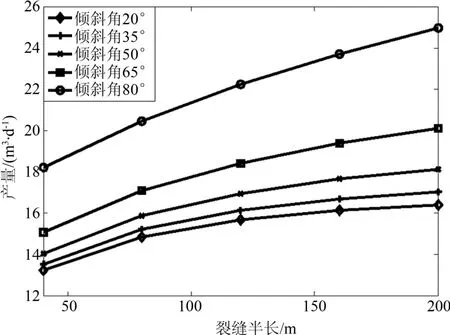
图11 不同裂缝半长下产量Fig.11 Productivity with different fracture length

5 结论

1）井筒存在压力损失时的产量比井筒无限导时产量差距较大，且沿井筒产量呈上大下小分布.

2）裂缝半长较大时，裂缝导流能力的增大会显著增加生产井的产量；裂缝半长较小时，产量增加不明显；对于裂缝半长较大的裂缝，提高裂缝导流能力尤为重要.无论裂缝半长大小，生产井产量随裂缝导流能力的增加有最大值，达到最大值后，产量不再增加.

3）井斜角小于60°时，井产量随井斜角产量增大而缓慢增加；井斜角大于60°时产量增加变快.单井产量随裂缝半长的增加而增大，且与裂缝半长呈直线关系.

［1］Niu Zengqian，Sui Xiangyun，Zhang Ping，et al.Research of fracturing technics for high angle deviated hole［J］.Oil Drilling ＆Production Technology，2005，27（5）：61－63.

［2］Yan Jinchuan，Diao Su，Zhu Liping，et al.Optimization and field application of hydraulic fracturing design of directional wells ［J］.Petroleum Geology and Recovery Efficiency，2008，15（5）：102－104.

［3］Diao Su，Yan Jinchuan，Ren Shan，et al.Research and field application on hydraulic fracturing technology of directional wells in western region of Sichuan［J］.Journal of Southwest Petroleum University（Science＆Technology Edition），2009，31（1）：111－115.

［4］Cinco H，Ramey H J，Miller F G.Unsteady-state pressure distribution created by a well with an inclined fracture［J］.SPE 5591，1975.

［5］Habte A D，Dinh A V，Tiab D.Pressure analysis of a well with an inclined asymmetric hydraulic fracture using type curves ［J］.SPE 140638，2010.

［6］Dinh A V，Tiab D.Pressure analysis of well with an inclined hydraulic fracture［J］.SPE 120540，2008.

［7］Zhang Yi.Research on productivity of horizontal and high deviated hydraulic fractured well［D］.Chengdu：Southwest Petroleum University，2003.

［8］Liu Xiangping，Zhang Zhaoshun，Liu Xianger，et al.A model to calculate pressure drops of horizontal wellbore variable mass flow coupled with flow in a reservoir［J］.Journal of Southwest Petroleum Institute，2000，22（2）：36－39.

［9］Huang Shijun，Cheng Linsong，Zhao Fenglan，et al.The flow model coupling reservoir percolation and variable mass pipe flow in production section of the stepped horizontal well［J］.Journal of Hydrodynamics，2005，20（4）：463－471.

［10］Novvy R A.Pressure drop in horizontal wells：When can they be ignored？［J］.SPE 24941，1992.

［11］Dikken B J.Pressure drop in the horizontal wells and its effects on their production performance［J］.JPT，1990：1426－1433.

［12］Yu Lexiang，Zhou Letian，Zhang Qi，et al.Pressure gradient model for variable mass fluid flow in horizontal wellbore［J］. Journal of University of Petroleum，China，2001，25（4）：47－50.

［13］Prats M，Hazebrock P，Strickler W R.Effect of vertical fractures on reservoir behavior-imcompressible-fuild case［J］.SPEJ，1962，22（5）：87－94.

［14］Lian Peiqing，Tong Dengke，Cheng Linsong，et al.A coupling model low permeability reservoir and fractured horizontal wellbore in nonsteady state［J］.Chinese J Comput Phys，2010，27（2）：203－210.

［15］Cheng Linsong，Pi Jian，Lian Peiqing，et al.A computational method of productivity of horizontal well in naturally fractured reservoirs［J］.Chinese J Comput Phys，2011，28（2）：230－236.

［16］Ye Shuangjiang，Jiang Hanqiao，Li Junjian，et al.Productivity calculation of infill horizontal wells in mixed well pattern［J］. Chinese J Comput Phys，2011，28（2）：693－697.

［17］Du Dianfa，Li Dongdong，Shi Dayou，et al.A study on heavy oil well test［J］.Chinese J Comput Phys，2011，28（3）：385－396.

A Coupling Flow Model of Finite-conductivity Fractured Directional Well

JIA Pin，CHENG Linsong，HUANG Shijun，FANG Sidong
（Faculty of Petroleum Engineering，China University of Petroleum（Beijing），Beijing 102249，China）

Considering artificial fracture，inclined wellbore and formation coupling flow，flow to directional well is divided into three parts：Flow from reservoir to fracture，flow in fracutre and variable mass flow in production pipe.Principles of potential superposition and mirror reflection as well as the concept of infinitesimal line congruence are used to model flow from reservoir to fracture and potential distribution in reservoir.By discreting fracuture to 2D grid，boundary theory is used to couple flow dynamics in fracture with variable mass flow in inclined pipe.A comprehensive coupling model for finite-conductivity fractured directional well is shown. Iteration method is used to solve the model.A practical case shows that for vertical fracutre result of coupling model agrees with that of Prats method.Fracture conductivity and inclined angle have great effects on productivity and pressure.

fractured directional well；finite-conductivity fracutre flow；coupling flow model；discreted grid；productivity

date：2013－09－17；Revised date：2013－11－27

TE312

A

2013－09－17；

2013－11－27

国家973（2013CB228000）及国家自然科学基金（51174215／E0403）资助项目

贾品（1990－），男，硕士研究生，从事油藏工程和渗流理论研究，E-mail：jiapin1990＠163.com

1001-246X（2014）05-0559-08