基于简单波的无限长竖直管道内检测器运动状态研究

杨 超，刘红旗

（机械科学研究总院 北京 100044）

基于简单波的无限长竖直管道内检测器运动状态研究

杨 超，刘红旗

（机械科学研究总院 北京 100044）

针对管道内检测器（包括输油和输气管道）通过盾构井时运行状态，建立了理想输气管道内检测器突然转向无限长竖直管段物理模型。基于简单波理论对该物理模型的运动状态进行了研究，并采用有限体积法进行了波动影响区的验证。分析结果表明：检测器在突然转向无限长竖直管段后会失去平衡，开始一段加速度逐渐减小的加速运动，但很快有达到另一种平衡态。

管道内检测器；盾构井；简单波；有限体积

0 引言

管道内检测器[1]是依靠压差在管道内移动的自走式检测仪器，广泛应用于石油、天然气管道的在线在役缺陷检测。检测器（包括输油和输气管道）在管道内的运动是依靠检测器前后的压差驱动的，压差作用在检测器上的推力正好能克服检测器和管道内壁的摩擦阻力，使检测器在管道内可以匀速（近似）前行。当检测器沿着水平管道运行到穿越峡谷、河流的盾构竖井时，检测器会在自身重力作用下加速，但其后的运动状态如何，检测器触底时速度是多少，检测器会受多大的冲击，是否安全等，这些一直困扰着管道检测人员。

笔者受某管道检测施工单位委托，对检测器突然竖直转向后的运动状态进行了研究，本文依据简单波理论对水平运动的检测器突然转向无限深度的竖直盾构井后运动状态进行了研究。

1 简单波动理论介绍

气体的扰动是以波的形式在流场中传播的，波速等于当地声速[2]。从物理上讲，当扰动仅从一个方向向均匀流动区域传播时，就产生了简单波[3,4]。简单波可分为四类：右行稀疏波，右行压缩波；左行稀疏波，左行压缩波 （一般沿流速方向为右行）。

右行波特征特征方程为：

其中：x—位移，距波源的距离；t—时间，波传播时间；v—流体速度；c—当地声速。式（1）积分后得：

在右行波区内有一黎曼不变量α：

其中：γ—气体比热比。同理，左行波特征方程为：

在左行波区内也有一黎曼不变量β：

2 竖直管段检测器等效物理模型

根据检测器实际运行经验可知：检测器刚刚转向到无限深竖直盾构井后可还依然保持原有运动速度，但此时重力的方向和运动速度方向一致，成了检测器加速的动力，其物理模型可以等效为在水平匀速运动的检测器突然施加一个大小为Mg，方向沿着运行方向的推力见图1。此时，检测器产生一个沿着运动方向大小为g的加速度。根据简单波理论，相当于检测器给了两端的气体一个扰动（波源），检测器两端的气体由一维定常流动变为了一维非定常流动[2]，检测器左端的气体形成了左向的稀疏波，检测器右端的气体形成了右向压缩波[5]。

图1 竖直管段等效模型Fig.1 Equivalent model of vertical pipe section

3 基于简单波检测器运动规律

根据简单波的性质[3]，检测器右端气体满足以下规律：

左端气体满足以下规律：

其中：v1—距离检测器 （波源）x处左向稀疏波的波速；v2—距离检测器 （波源）x处右向压缩波的波速；P10—检测器左端距离检测器（波源）x处的初始气体压强（常态下气压）；P20—检测器右端距离检测器 （波源）x处原始气体压强（常态下气压）；P1—检测器左端距离检测器 （波源）x处t时刻的气体压强；P2—检测器右端距离检测器（波源）x处t时刻的气体压强；c0—常态下的气体声速。根据检测器的受力分析，可得检测器的加速度：

式（7）～（11）是检测器突然转向无限深竖直管道（突然受F=mg作用）后的运动状态方程。联立（7）～（11），通过迭代求解可求解处检测器的加速度a,进而对a积分可以求得检测器的速度v。

下面以具体实例进行说明。无限长管道（图1），管径D=1016mm，管道中气体压强P1=7MPa，40寸检测器重m=4吨，总的阻力 f=20KN，检测器和气体开始以 7. 23m/s的速度匀速运动，在时间t=0时，突然在检测器突然转向无限深竖直管道 （突然受作用，方向沿气流方向），通过迭代求解可得检测器加速度曲线如图3所示。采用Matlab进行曲线拟合可得检测器加速度：

从图2可以看出，检测器突然转入无限深竖直管段（突然受作用，方向沿气流方向），检测器的平衡状态被打破，开始了加速度逐渐减小的加速运动，大约0.6s后再次区域平衡，此时，P1=6.9756MPa，P2=6.9997MPa。此时检测器速度V=8.0812m/s2；检测器位移S=5.2m。

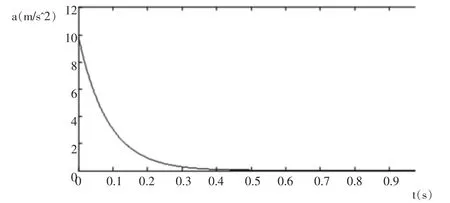
图2 检测器加速度曲线图Fig.2 Accelerating curve of detector

根据简单波理论，波源的有效影响区为L=340×0.6= 204m，影响区以外管段内气体压力不变。

4 基于有限体积法的有效影响区验证

检测器趋于平衡时，影响区内压强P是位移x的函数。对左端气体任取一有限体积[6]Sl，它的受力情况如图3所示。 Ps为沿程压力损失。根据牛顿第二定律，S1满足：

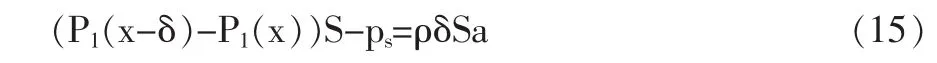
其中：P1（x-δ）—有限体积左侧气体压强；P1（x）—有限体积右侧气体压强；ps—沿程压力损失；S—管道截面积；ρ—气体密度；δ—有限体积气体长度；a—基于简波计算出的气体加速度。

图3 有限体单元积受力情况Fig.3 The force balance of finite volume element

根据式（15），运用Matlab进行迭代运算可得稀疏段压强分布如图4所示。同理，可求得压缩波的影响区如图5所示。

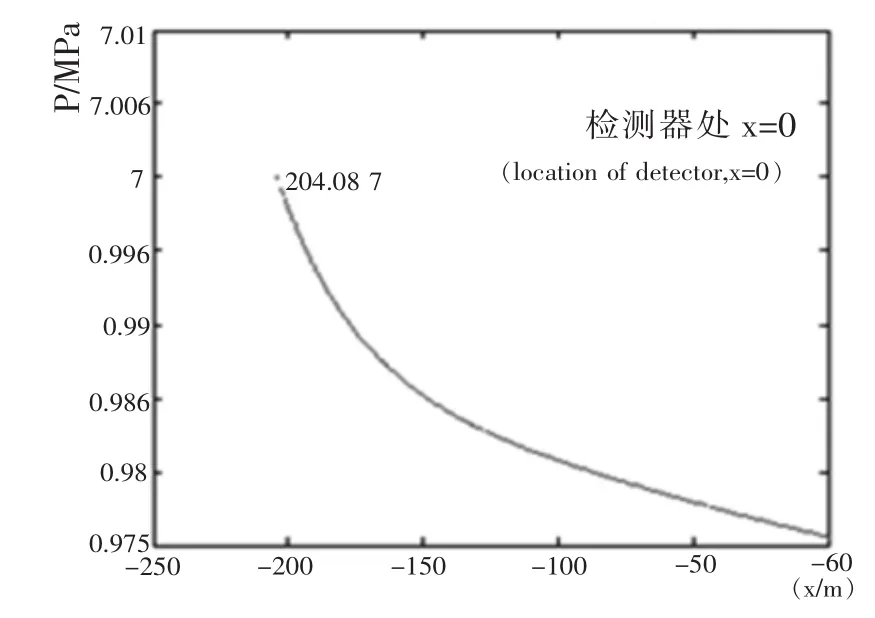
图4 有限体积法计算的稀疏波影响区Fig.4 Rarefaction wave affected zone

图5 有限体积法计算的压缩波影响区Fig.5 Compression wave affected zone

从图4、图5可以看出：在假定波动理论得到的加速度曲线的情况下，运用有限体积法进行影响区域验证，两种方法得到的影响区域基本吻合。

5 结论

以上分析表明：无限长管道内检测器突然转向竖直管段（突然受作用），相当于在流体中形成一个激励源，在检测器两端分别形成稀疏波和压缩波。

在稀疏波影响区内，压力向右衰减，速度大小向左衰减；在压缩波影响区内，压力向右衰减，速度大小也向右衰减。

检测器两端左端压强减小，右端压强增大。一定时间后检测器再次趋于平衡（加速度趋近于0）。本文中实例大约0.6s后趋于平衡，末速度为8.0812m/s。两端影响区各204m左右。

此后检测器引起的激励以波的形式继续向两端传播（能量损失完以前），同时影响区范围内形成的压力和速度包络波也向两端传播（能量损失完以前）。

[1]刘宝余．输气管道内检测器设计及理论研究[D]．北京：中国石油大学，2010.

[2]王保国，刘淑艳，等．气体动力学[M]．北京：北京理工大学出版社，2005．

[3]卢芳云．一维不定常流体动力学教程[M]．北京:科学出版社，2006．

[4]Gabi Ben,Ozer lgra,Tov Elperin.Handbook of Shock Waves.Academic Press.2000.

[5]李维新．一维不定常流与冲击波[M]．北京：国防工业出版社，2003．

[6]R.Keck,D.Hietel.A projection technique for incompressible flow in the meshless finite volume particle method.Advances in Computational Mathematics,2004.

Research on Motion State of Detector in Infinite Vertical Pipeline Based on Simple Waves

YANG Chao，LIU Hong-Qi
（Mechanical Science Research Institute,Beijing 100044，China）

The physical model of detector in ideal gas pipeline turning suddenly to infinite vertical pipeline has been build in this paper to simulate the motion state of the in-pipe detector (including oil and gas pipeline)moving through the shield shaft.Research on motion state of this physical model based on the simple waves and the test of fluctuation affected zone based on the finite volume method have been achieved.Results show that the detector will lose balance when turning abruptly to the infinite vertical pipeline and will reach equilibrium soon through a length of acceleration movement in which the accelerated speed diminishing.

detector in pipe；shield shaft；simple wave；finite volume method

TU311

：Adoi:10.3969/j.issn.1002-6673.2014.03.043

1002－6673（2014）03－109－03

2014－03－01

项目来源：国家科技支撑计划项目（2012BAH08F01）

杨超，男，博士研究生，专业为机械设计及理论；刘红旗，男，研究员，博士生导师，国务院特殊津贴专家。