基于人工神经网络的磷酸三丁酯络合萃取Np(Ⅳ、Ⅵ)的模拟
周羽,未根华,何辉,陈延鑫
1.哈尔滨工程大学核安全与仿真技术国防重点学科实验室,黑龙江哈尔滨150001; 2.中国原子能科学研究院放射化学研究所,北京102413
基于人工神经网络的磷酸三丁酯络合萃取Np(Ⅳ、Ⅵ)的模拟
周羽1,未根华1,何辉2,陈延鑫2
1.哈尔滨工程大学核安全与仿真技术国防重点学科实验室,黑龙江哈尔滨150001; 2.中国原子能科学研究院放射化学研究所,北京102413
近年来,核燃料后处理的计算机模拟研究成为世界各国研究核燃料后处理工艺过程的重要手段。本工作以磷酸三丁酯为萃取剂、煤油为稀释剂的混合有机萃取剂,在HNO3介质中络合萃取Np(Ⅳ、Ⅵ)的体系中,利用BP人工神经网络将萃取平衡分配比和萃取操作条件如初始硝酸浓度、初始Np(Ⅳ、Ⅵ)浓度、初始U(Ⅵ)浓度及温度进行了关联。建立了该体系下磷酸三丁酯络合萃取Np(Ⅳ、Ⅵ)的人工神经网络模型,并用该模型计算且检验了不同萃取条件对平衡分配比的影响。结果表明:在25~60℃、水相c0(HNO3)为0.1~11 mol/ L、水相初始铀质量浓度为0~210 g/L时,该人工神经网络模型可以对Np(Ⅳ、Ⅵ)萃取分配比进行预测,具有较高的计算精度。经过文献Np(Ⅳ、Ⅵ)萃取平衡分配比实验值检验,其检验平均相对误差在2%以内。
人工神经网络;镎;磷酸三丁酯;络合萃取
237Np的辐照产品238Pu是比功率很高(0.5 W/g)的α放射源,其广泛应用于航天航空、舰艇、医疗卫生及军事领域,近年来需求量日益增加[1]。Np在天然环境中并不存在,而对于3.5%235U的动力堆核燃料,辐照燃耗为33 000 MWd/t,会产生445 g/t(以重金属计)[2]。并随着燃耗增加,其Np的产额会以燃耗的1.5次方成正比增长[3]。因此,从乏燃料后处理流程中提取237Np就成为众多提取途径中非常重要的一条。但由于后处理体系中的组分复杂、放射性毒性高,因此各国都选用计算机模拟计算或仿真的手段进行预测研究。目前许多代码都成功的模拟了Np的萃取行为和过程。如:法国马库尔和英国塞拉菲尔德研究队伍都成功地实现了在Purex流程中Np的萃取行为的控制和模拟,并成功实现了“镎管理”[4-5]。这项工作是依赖于经过验证,且准确、可靠的分析仿真程序,例如法国原子能委员会(CEA)的PAREX和英国BNFL(英国核燃料公司)的Speed Up程序。这些程序均是双方在大量的Np分配数据和氧化还原动力学数据的基础上独立开发的。其中,Purex流程中共去污分离循环(U、Np、Pu共萃)的工艺条件由法国CEA提供[6],铀线中铀中去镎的工艺条件由BNFL提供[7-8]。前者的程序在法国ATALANTE(CEA马库尔)的热室(Chaîne Blindée Procédé,简称CBP)中,经过乏燃料元件溶解液和脉冲柱实验验证。随后,在英国塞拉菲尔德的热室中重现。张虎等[9]也用程序模拟了Purex流程中共去污过程的萃取行为,并用微型混合澄清槽的台架实验验证了该程序。综上,各个Np萃取过程的仿真模拟程序,都需要建立相应的Np萃取过程的分配比计算程序或预测程序。因此,本工作拟应用BP人工神经网络建立不同温度下Np(Ⅳ、Ⅵ)的萃取平衡分配比模型,以期为后处理工艺及提镎工艺提供一定的预测分析手段和方法。
1 BP人工神经网络
1986年Rumelhart等提出一种人工神经网络(ANN)的误差反向传播训练算法(BP算法),系统解决了多层网络中隐含单元连接权的学习问题,由此算法构成的网络被称为BP网络。BP网络是向前反馈网络中的一种,被广泛应用于非线性建模、函数逼近、模式分类等领域中[10]。其典型结构示于图1。
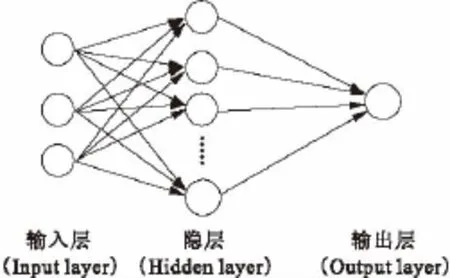
图1 典型BP网络结构图Fig.1Typical BP network structure
1.1 Np萃取模型的建立
BP人工神经网络亦广泛应用于液液溶剂萃取过程,利用其优良的函数逼近能力,用来描述萃取过程操作条件与平衡分配比的关联[11]。
1.1.1 Np(Ⅳ,Ⅵ)萃取平衡分配比数据本工作采用的Np(Ⅳ,Ⅵ)萃取平衡分配比数据来源于文献[12]。其中Np(Ⅳ)萃取平衡分配比数据287组,Np(Ⅵ)萃取平衡分配比数据321组。本工作建立的BP人工神经网络中,分别使用240组Np(Ⅳ)萃取平衡分配比数据和260组Np(Ⅵ)萃取平衡分配比数据作为学习样本。余下数据作为该模型的检验样本。学习样本与检验样本均为随机抽取。
1.1.2 平衡分配比数据的标准化处理BP算法的学习过程分为两个阶段:(1)正向传播过程,即给出输出信息通过输入层经隐层处理并计算每个单元的实际输出值;(2)反向过程,若输出层未能得到期望的输出值,则逐层递归地计算实际输出与期望输出之差(误差),以便调节权值。虽然这一过程在数学层面保障了误差的反向传播,但它仍然是属于前馈型网络,故它不是非线性动力学系统,而只是一个非线性映射。它也存在不少问题:(1) BP算法按均方误差的梯度下降方向收敛,可能导致局部极小;(2)学习收敛速度慢。为使BP神经网络收敛更快,本工作采用了min-max标准化处理分配比数据,即将输入与输出数据均按式(1)处理,使其映射为区间[0,1]的数据集合。
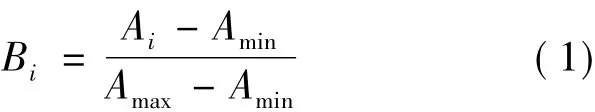
式中:Ai,Bi分别表示输入和输出数据,如:初始硝酸浓度、温度等;Amin、Amax分别表示输入数据的最小值和最大值。
1.2 Np萃取过程的BP神经网络算法分析及建立
本工作应用Matlab人工神经网络工具箱来建立Np(Ⅳ、Ⅵ)萃取过程的模型。由于标准BP神经网络模型收敛周期长,学习周期多,亦采用了多种提高训练速度的方法来改进BP模型,使其在达到准确度的前提下,效率相对较高。将标准化处理之后水相c0(HNO3)、c(U)、c(Np(Ⅳ))和温度作为输入变量,将标准化处理之后四价镎的萃取平衡分配比作为输出变量,采用以下参数来建立BP神经网络:神经网络的设定神经元数目在1~18;隐层传递函数为Logsig、Tansig;训练目标最小误差为10-3;学习速率在0.1~0.5;输出层传递函数为Purelin。训练算法分别采用标准BP算法(Traingd)、共轭梯度算法(Trainscg)、L-M算法(Trainlm)、动量梯度下降法(Traingdm)、自适应梯度算法(Traingda)分析神经网络收敛和优化后对Np(Ⅳ、Ⅵ)萃取过程平衡分配比的影响。不同神经网络算法的收敛曲线示于图2。由图2可知,标准BP算法(Traingd)的收敛周期最长,而共轭梯度算法(Trainscg)和L-M算法(Trainlm)收敛速度明显快得多。从HNO3介质中Np(Ⅳ,Ⅵ)、含铀HNO3介质中Np(Ⅵ)的不同训练算法的收敛周期的比较来看,也是L-M算法收敛速度最明显。故本工作主要讨论基于L-M法的神经网络模型。
2 结果与讨论
2.1 Np(Ⅳ)萃取过程神经网络模型结果及优化
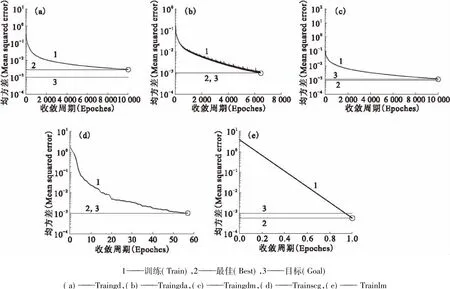
图2 含铀HNO3介质中Np(Ⅳ)不同神经网络训练算法的收敛曲线Fig.2Convergence curves at variable training algorithms of Np(Ⅳ)in nitric acid and uranium medium ANN model

图3 HNO3介质中Np(Ⅳ)神经网络模型不同隐层传递函数的收敛曲线Fig.3Convergence curves at variable transfer functions of hidden layer of Np(Ⅳ)in HNO3medium model
2.1.1 HNO3介质中Np(Ⅳ)萃取分配比模拟不同隐层神经元数目时,Np(Ⅳ)萃取平衡分配比模拟结果的相对误差列入表1。由表1可知,在隐层神经元数目为15时,对Np(Ⅳ)萃取过程的平衡分配比造成的相对误差最小,为0.26%。不同隐层传递函数的收敛曲线示于图3。由图3可见,Tansig函数的收敛周期更小,为123,并且收敛曲线更加平滑。因此,在HNO3介质中Np(Ⅳ)的神经元模型中的隐层传递函数采用Tansig函数。2.1.2含铀HNO3介质中Np(Ⅳ)萃取分配比模拟不同隐层神经元数目时,含铀HNO3介质中Np (Ⅳ)萃取平衡分配比模拟结果的相对误差列入表2。由表2可知,在隐层神经元数目为16时,对Np (Ⅳ)萃取过程的平衡分配比造成的相对误差最小,为0.47%。不同隐层传递函数的收敛曲线示于图4。由图4可见,Tansig函数的收敛周期更小,为443。
因此,在含铀HNO3介质中Np(Ⅳ)的神经元模型中的隐层传递函数应采用Tansig函数。
2.1.3 学习速率优化学习速率的作用是不断调整权值的阈值,如果变化太大或过小均会对模型的收敛周期产生影响。因此,在建立Np(Ⅳ)神经网络模型基础上,通过改变学习速率,比较计算结果收敛速度,选择收敛速度快且稳定的作为优化后的学习速率,结果列入表3。由表3可见,HNO3介质和含铀HNO3介质中,两个模型均是在
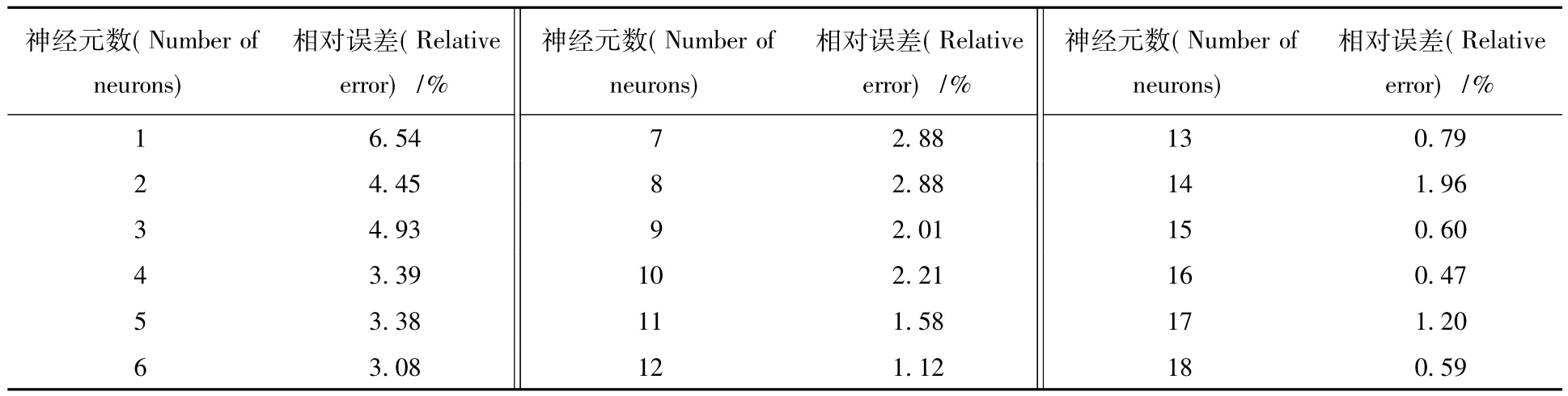
表2 神经元数对含铀HNO3介质中Np(Ⅳ)萃取平衡分配比模拟的影响Table 2Influence on distribution ratio of Np(Ⅳ)in nitric acid and uranium medium at variable hidden layer number of ANN
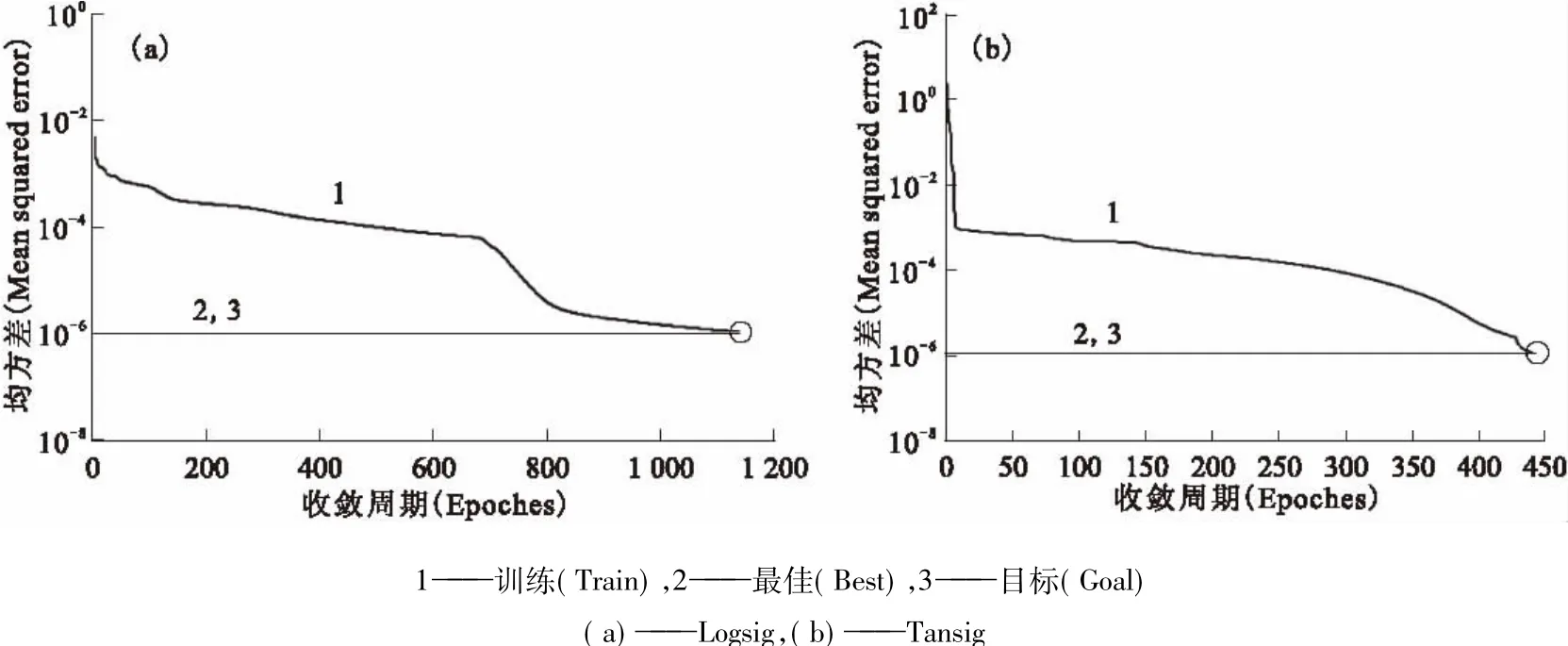
图4 含铀HNO3介质中Np(Ⅳ)神经网络模型不同隐层传递函数的收敛曲线Fig.4Convergence curves at variable transfer functions of hidden layer of Np(Ⅳ)in HNO3and uranium medium model
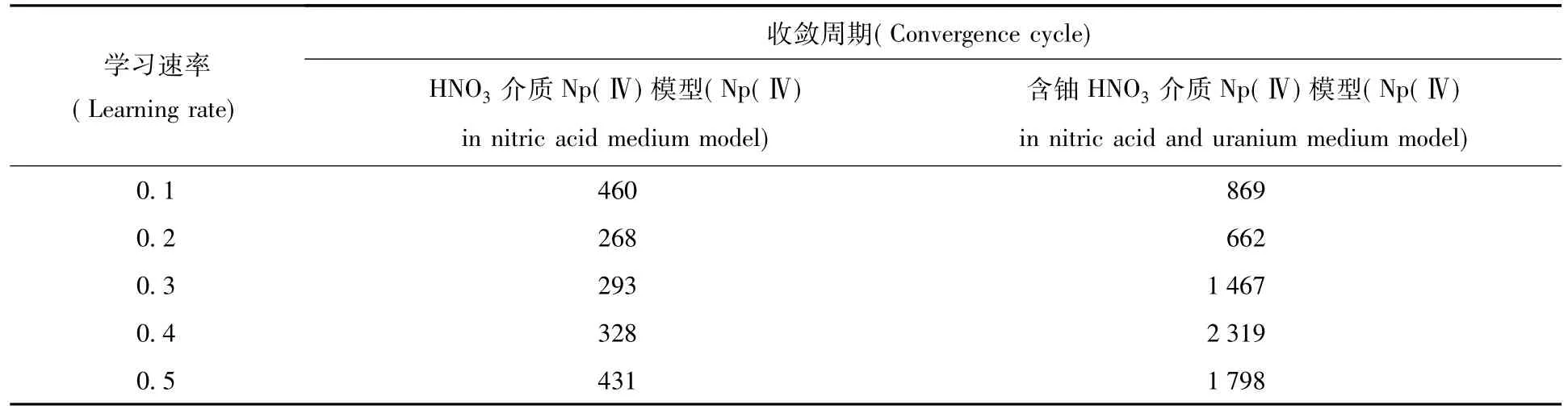
表3 学习速率对Np(Ⅳ)神经网络模型收敛周期的影响Table 3Influence on convergence cycles of Np(Ⅳ)ANN at variable learning rate
学习速率为0.2时收敛最快,故优化后的两个神经网络模型均采用学习速率为0.2。
2.2 Np(Ⅵ)萃取过程神经网络模型结果及优化
2.2.1 HNO3介质中Np(Ⅵ)萃取分配比模拟不同隐层神经元数目时,Np(Ⅵ)萃取平衡分配比模拟结果的相对误差列入表4。由表4可知,在隐层神经元数目为18时,对Np(Ⅵ)萃取过程的平衡分配比造成的相对误差最小,为0.56%。不同隐层传递函数的收敛曲线示于图5。由图5可见,Tansig函数的收敛周期更小,且Logsig函数在精度比较低的情况下就停止了训练。因此,在HNO3介质中Np(Ⅵ)的神经元模型中的隐层传递函数应采用Tansig函数。
2.2.2 含铀HNO3介质中Np(Ⅵ)萃取分配比模拟不同隐层神经元数目时,含铀HNO3介质中Np(Ⅵ)
萃取平衡分配比模拟结果的相对误差列入表5。
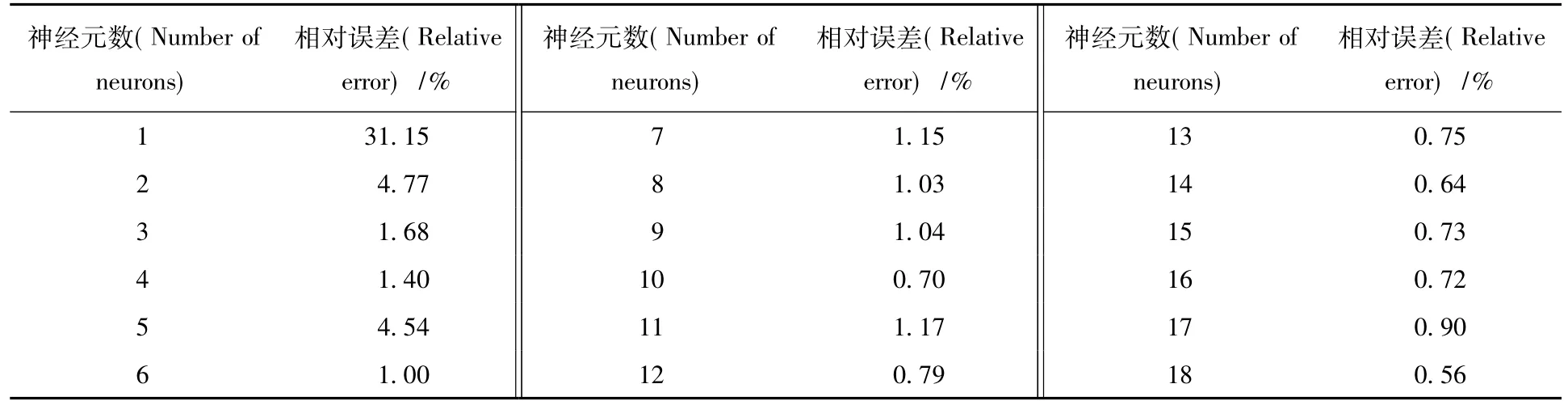
表4 神经元数对HNO3介质中Np(Ⅵ)萃取平衡分配比模拟的影响Table 4Influence on distribution ratio of Np(Ⅵ)in nitric acid medium at variable hidden layer number of ANN
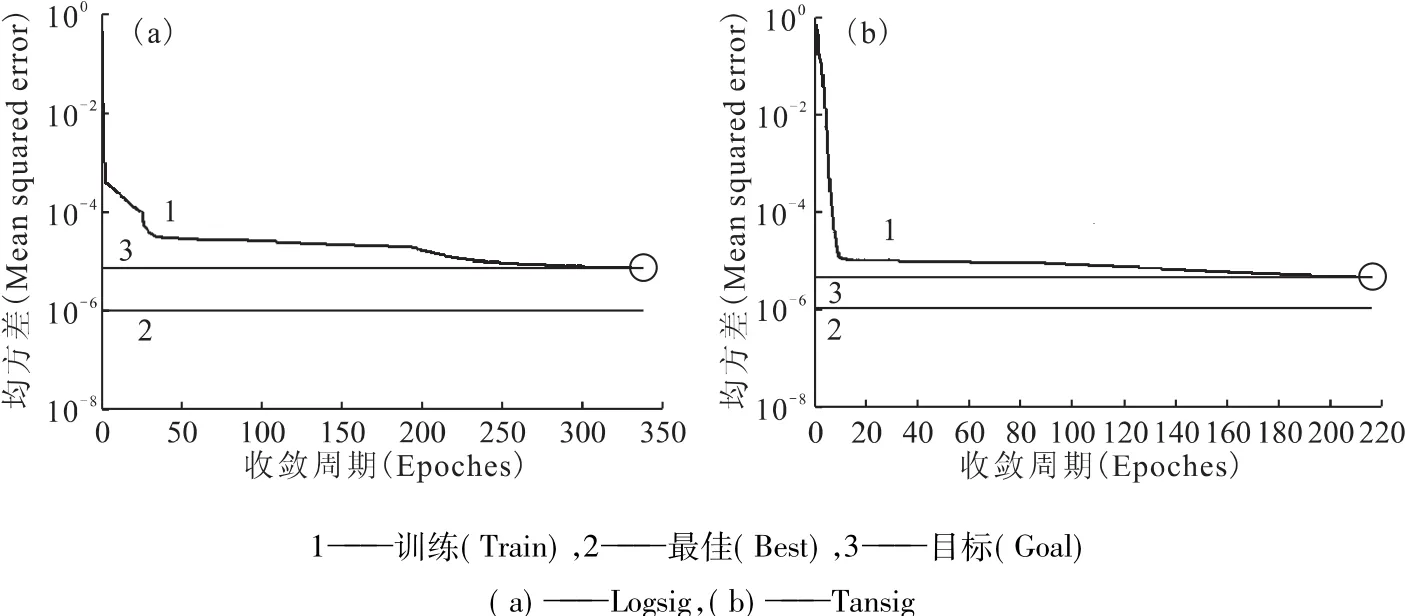
图5 HNO3介质中Np(Ⅵ)不同隐层传递函数的收敛曲线Fig.5Convergence curves at variable transfer functions of hidden layer of Np(Ⅵ)in HNO3medium model
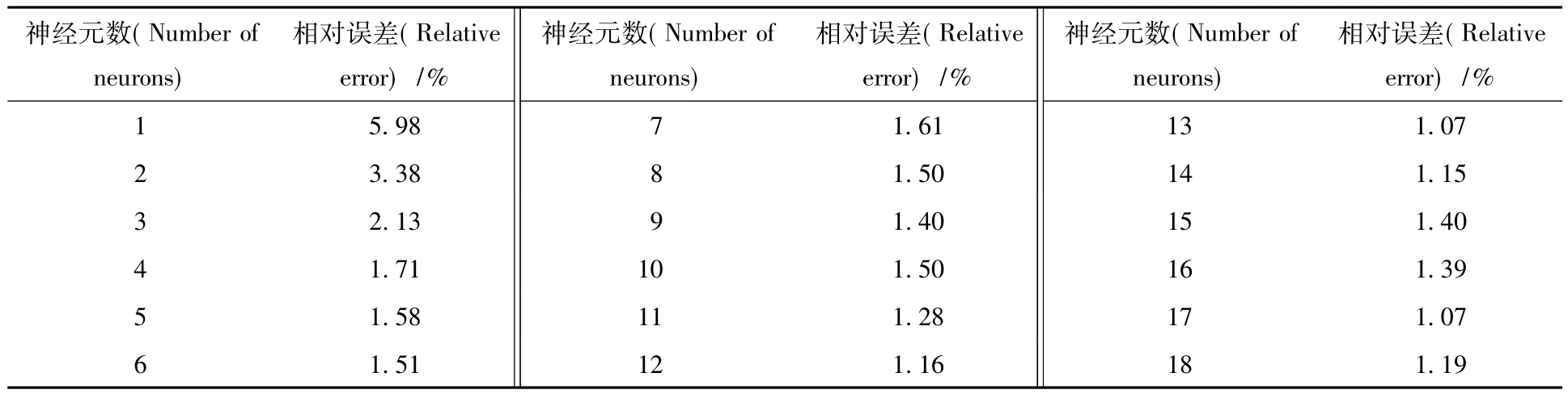
表5 神经元数对含铀HNO3介质中Np(Ⅵ)萃取平衡分配比模拟的影响Table 5Influence on distribution ratio of Np(Ⅵ)in nitric acid and uranium medium at variable hidden layer number of ANN
由表5可知,在隐层神经元数目为13时,对Np(Ⅵ)萃取过程的平衡分配比造成的相对误差最小,为1.07%。不同隐层传递函数的收敛曲线示于图6。由图6可见,二者收敛周期没有较大差别,而Logsig函数的收敛曲线更加平滑。因此,在含铀HNO3介质中Np(Ⅵ)的神经元模型中的隐层传递函数采用Logsig函数。
2.2.3 学习速率优化不同学习速率Np(Ⅵ)神经网络模型收敛周期列入表6。由表6可知: HNO3介质中Np(Ⅵ)模型在学习速率为0.1时收敛最快;含铀HNO3介质中,Np(Ⅵ)模型在学习速率为0.2时收敛最快。

图6 含铀HNO3介质中Np(Ⅵ)不同隐层传递函数的收敛曲线Fig.6Convergence curves at variable transfer functions of hidden layer of Np(Ⅵ)in HNO3and uranium mudium model
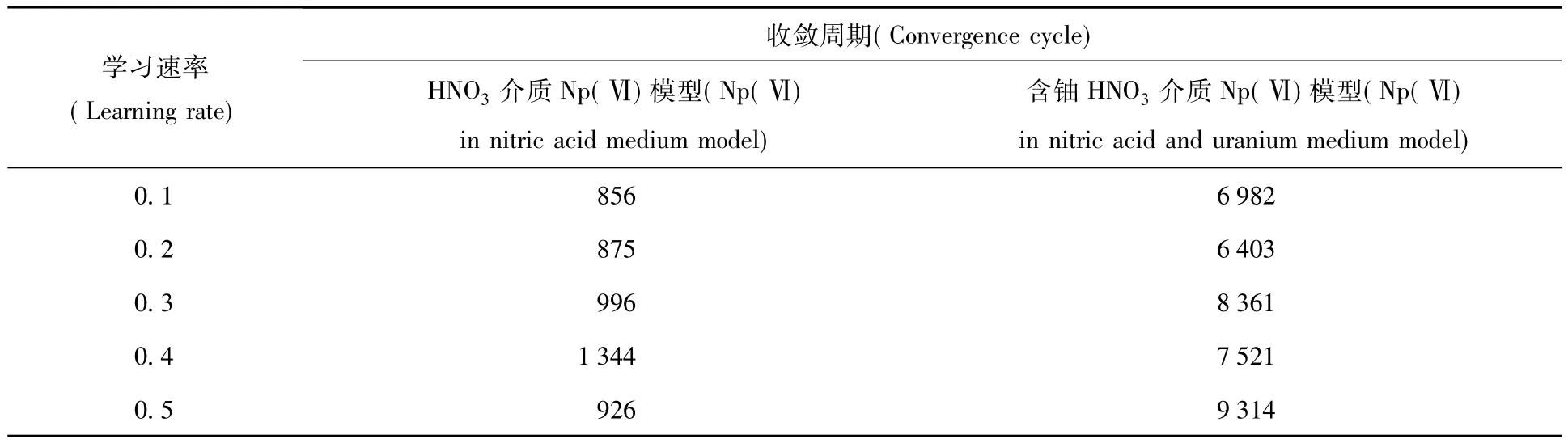
表6 学习速率对Np(Ⅵ)神经网络模型收敛周期的影响Table 6Influence on convergence cycles of Np(Ⅵ)ANN at variable learning rate
2.3 Np(Ⅳ、Ⅵ)人工神经网络模型的检验
检验样本数据来源于文献[12],选取未用于学习样本的数据,并且随机抽取。以检验样本的初始条件作为Np(Ⅳ、Ⅵ)人工神经网络模型的输入条件,进行预测计算。以检验样本的Np(Ⅳ、Ⅵ)各条件下的萃取平衡分配比为检验目标。图7为不同神经网络模型的预测值与检验样本检验目标的检验曲线。在HNO3介质中Np(Ⅳ)和Np(Ⅵ)的人工神经网络模型,分别选取了温度范围从25~60℃、硝酸浓度从0~11 mol/L的检验样本36组和34组。由图7(a,b)可知:HNO3介质中Np(Ⅳ)分配比人工神经网络模型的检验平均误差为1.6%;HNO3介质中Np(Ⅵ)分配比人工神经网络模型的检验平均误差为1.94%。在含铀的HNO3介质中Np(Ⅳ)和Np(Ⅵ)的人工神经网络模型,分别选取了温度范围从25~60℃、HNO3浓度从0~11 mol/L的检验样本60组和61组。由图7(c,d)可知:含铀HNO3介质中Np(Ⅳ)分配比人工神经网络模型的检验平均误差为1.5%;含铀HNO3介质中Np(Ⅵ)分配比人工神经网络模型的检验平均误差为1.4%。因此,Np(Ⅳ、Ⅵ)人工神经网络模型预测值与检验值相差非常小,其检验平均相对误差均在2%以内。
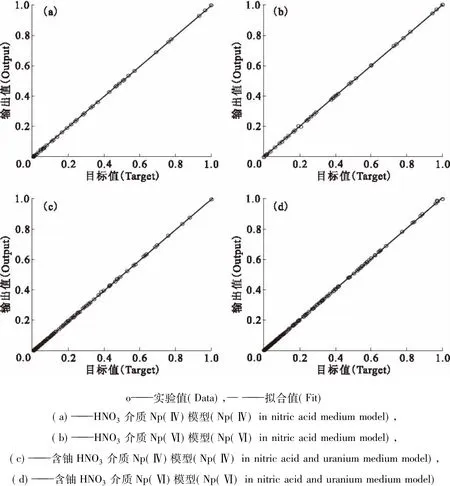
图7 不同神经网络模型检验结果Fig.7Test results at variable Np(Ⅳ,Ⅵ)ANN model
3 结论
(1)应用Matlab人工神经网络工具箱建立和优化了Np(Ⅳ、Ⅵ)分别在磷酸三丁酯/煤油-HNO3体系和磷酸三丁酯/煤油-硝酸铀酰-HNO3体系中的BP人工神经网络模型。
(2)经过文献Np实验分配比数据与计算预测值的检验,在25~60℃、水相c0(HNO3)为0.1~11 mol/L、水相初始铀质量浓度为0~210 g/L时有较好的预测能力,其检验平均相对误差小于2%。
(3)该人工神经网络模型有较高的计算准确度和令人满意的计算速度,可以在实际工艺过程分析中应用。
[1]Lange R,Carroll W.Review of recent advances of radio-isotope power systems[J].Energy Conversion and Management,2008,49(3):393-401.
[2]Wymer R G,Vondra B L.Light water reactor nuclear fuel cycle[M].New York:CRC Prees Inc,1981: 68.
[3]Ochsenfeld W,Petrich G,Schmidt H J,et al.Neptunium decontamination in a uranium purification cycle of a spent fuel reprocessing[J].Sep Sci Technol,1983,18(14&15):1685.
[4]Sengupta A K.Ion exchange and solvent extraction:a series of advances[M].Boca Raton,Florida:CRC Press,2007:4-5.
[5]Baron P,Lorrain B,Boullis B.Progress in partitioning:activities in ATALANTE[C]∥9th ATALANTE Conference.France:OECD/NEA IEM,2006:25-29.
[6]Nuclear Energy Agency,OECD.French R&D on the partitioningandtransmutationoflong-lived radionuclides:NEA No.6210[R].France:NEA/ OECD,2005.
[7]Fox O D,Jones C J,Birkett J E,et al.Advanced PUREX flowsheets for future Np and Pu fuel cycle demands.In Separations for the Nuclear Fuel Cycle in the 21stCentury[G]∥Lumetta G J,et al.Eds.ACS Symposium Series,Washington:American Chemical Society,2006,933:89-102.
[8]Taylor R J,Denniss I S,Wallwork A L.Neptunium control in an advanced Purex process[J].Nucl Energy,1997,36(1):39-46.
[9]Zhang Hu,Ye Guo-an,Li Li,et al.Simulation of the neptunium behavior during the first solvent extraction cycle in the PUREX process[J].J Radioanal Nucl Chem,2013,295(2):883-888.
[10]闫平凡,张长水.人工神经网络与模拟进化计算[M].北京:清华大学出版社,2000:14-32.
[11]管国锋,马晓龙,姚虎卿.磷酸三丁酯络合萃取丁酸的研究[J].南京化工大学学报(自然科学版),2000,21(06):823-827.
[12]Dressler P,Kolarik Z,Karlsruhe K.Purex process related distribution data on neptunium(Ⅳ,Ⅵ):KFK-4667[R].Karlsruhe:Kernforschungszentrum,1990.
Simulation of Complex Extraction of Neptunium(Ⅳ,Ⅵ) With Tributyl Phosphate Based on Artificial Neural Networks
ZHOU Yu1,WEI Gen-hua1,HE Hui2,CHEN Yan-xin2
1.Fundamental Science on Nuclear Safety and Simulation Technology Laboratory,Harbin Engineering University,Harbin 150001,China; 2.China Institute of Atomic Energy,P.O.Box 275(26),Beijing 102413,China
Computer simulation of nuclear fuel reprocessing in recent years becomes an important means of study the nuclear fuel reprocessing process in the world.Tributyl phosphate as the extractant and kerosene as the diluent were selected for the complex extraction of neptunium(Ⅳ,Ⅵ).By using BP artificial neural networks(ANN),the equilibrium distribution ratio was correlated with the extraction operational conditions in the extraction system,such as initial concentration of nitric acid,neptunium(Ⅳ,Ⅵ)and uranium(Ⅵ),as well as temperature.The ANN model of extraction equilibrium ratio was established.Moreover,the effects of different extraction condition on the equilibrium distribution ratio were predicted by using the model.Theresults show that the proposed model can simulate the experimental data and predict the process of extraction well,in the range of experiment conditions,such as 25-60℃,0.1-11 mol/L HNO3and 0-210 g/L U(Ⅵ).After testing by the Np(Ⅳ,Ⅵ)extraction distribution ratio values from the literature,the mean relative error is less than 2%.
artificial neural networks;neptunium;tributyl phosphate;complex extraction
TL241.14;TP391.9
A
0253-9950(2014)03-0149-08
10.7538/hhx.2014.36.03.0149
2013-09-21;
2013-11-16
大厂重大专项资助项目(后处理流程各工艺单元数学模型和计算软件研制)(2010ZX06203-01)
周羽(1983—),男,重庆人,讲师,核燃料循环与材料专业

