基于粒子群-差异进化混合算法的电力系统无功优化

张燕，许伟伟

(河北工业大学控制科学与工程学院，天津300130)

基于粒子群-差异进化混合算法的电力系统无功优化

张燕，许伟伟

(河北工业大学控制科学与工程学院，天津300130)

针对传统粒子群算法中收敛速度快但易于陷入局部最优等特点，将差异进化算法与粒子群算法相结合，提出了一种粒子群-差异进化混合算法。该算法在粒子寻优过程中除跟踪个体极值和全局极值外，还跟踪粒子差异进化产生的第三个值;同时，当粒子在某一维上的速度小于给定值时，将重新初始化该维度粒子速度。建立了无功优化数学模型，并将合算法应用到无功优化中。通过MATLAB编程对IEEE-30节点系统进行优化计算，并与遗传算法和粒子群算法比较，结果表明本文提出的算法应用于无功优化拥有较快的收敛速度和全局寻优能力，具有广阔的发展前景。

粒子群;差异进化算法;无功优化;电压质量

1 引言

无功优化作为电力系统运行管理的一项重要内容，是保证电力系统安全、稳定、经济运行的重要手段。通过各国学者多年的研究和积累，提出了很多无功优化理论和方法，主要有动态规划法、线性规划法、邻域拓扑法、禁忌搜索算法、遗传算法和粒子群算法等［1］。粒子群算法(PSO)是Kennedy和Eberhart于1995年提出的一种多点搜索智能优化算法，该算法实现较容易，需要调节的参数较少，可按经验值设置合理参数，但其存在收敛精度低、容易陷入局部收敛等缺点［2］。本文针对传统粒子群算法所存在的上述缺点，将差异进化算法与粒子群算法相结合，提出了一种粒子群-差异进化混合算法，并将其应用到电力系统无功优化中。对IEEE-30节点系统进行仿真计算，结果表明，本文提出的算法可以有效降低网损，提高电压质量，具有广阔的应用前景。

2 无功优化的数学模型

电力系统无功优化的目标是通过调节控制变量各参数，使系统网损最小，节点电压维持在约束范围内，进一步改善电压质量，最大程度减少电能损耗，从而达到降低运行成本和提高电力系统稳定性的目的［3］。

本文无功优化以有功网损最小为目标函数，以发电机无功出力及负荷节点电压为状态变量，以发电机端电压、无功补偿电容器和有载调压变压器变比为控制变量，数学模型如下:

式中，N为系统节点数;Npv为发电机PV节点数;Gk(i，j)为支路k的电导;Vi、Vj为第i、j节点的运行电压;θij为节点i与节点j之间的电压角度差;λ1、λ2为越限的罚因子;Vimax、Vimin分别为节点电压Vi的上下限;Qimax、Qimin分别为发电机无功出力Qi的上下限;Vilim、Qilim分别为节点i的电压、无功限值，定义如下:

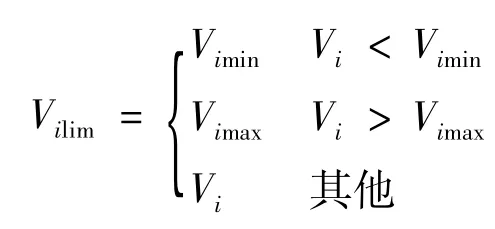
等式约束为:

式中，Gij为节点i和j之间的电导;Bij为节点i和j之间的电纳。

不等式约束为:

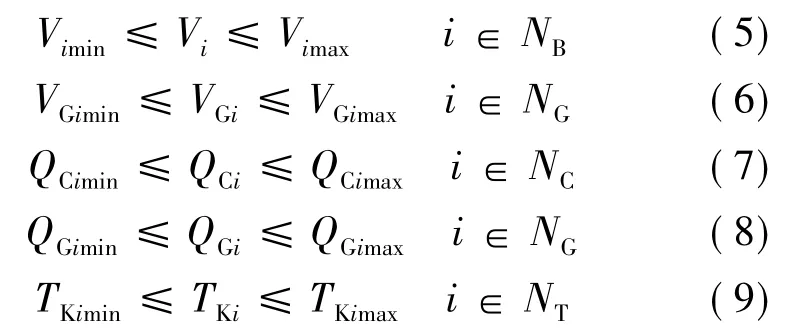
式中，NB、NC、NG、NT分别为总节点、补偿电容器节点、发电机节点和变压器支路集合;Vi为节点电压幅值;Vimin、Vimax分别为节点电压下限和上限;VGi为发电机端电压幅值;VGimin、VGimax分别为发电机端电压下限和上限;QCi为无功补偿容量;QCimin、QCimax分别为无功补偿下限和上限;QGi为发电机无功出力; QGimin、QGimax分别为发电机无功出力的下限和上限; TKi为变压器分接头位置;TKimin、TKimax分别为变压器分接头位置的下限和上限。

3 粒子群-差异进化混合算法

3.1 粒子群优化算法

PSO算法基本思想是首先初始化一群随机粒子，粒子跟踪个体极值和全局极值来更新速度与位置，通过逐步迭代找到最优解。在D维搜索空间当中，形成种群大小为m粒子群。其中，设第i个粒子在第j维位置为Xij，速度为Vij，粒子当前搜索到的个体最优位置即个体极值为Pij，粒子群当前最优位置即全局最优解为Pgj。其更新迭代计算式为:

式中，i=1，2，…，N;j表示粒子的第j维;k为迭代次数;c1、c2为加速因子，一般在0～2间取值，c1和c2是为了调节粒子向自身最好位置和全局最好位置飞行的步长;r1～u(0，1)、r2～u(0，1)为两相互独立的随机函数;w为惯性权重。为了降低粒子在进化过程中离开搜索空间的概率，粒子速度Vij通常限定在一定值域内，即Vij∈［－Vmax，Vmax］，搜索空间限定在［－Xmax，Xmax］内［4］。

3.2 差异进化算法

差异进化算法在处理连续变量优化问题上具有一定的优势，通过变异、交叉和选择对种群中个体进行循环操作，得到下一代种群，按照此法进化最后获得问题的最优解［5］。寻优机构与遗传算法类似，最大不同是差异进化算法主要通过操作染色体的差异向量来进行变异。

3.3 粒子群-差异进化混合算法

(1)粒子群-差异进化算法在粒子迭代过程中，在粒子跟随个体极值Pij和全局极值Pgj的基础上引入第三个值，通过以下方法产生:

式中，rand为0～1之间的随机数;cr为变异概率;k为1～D之间的随机数;D为最大维数;TVij为第i个粒子跟随的第三个值;P1j、P2j、P3j、P4j、P5j为随机从种群中选取的5个个体极值Pij;F取0.4。则粒子速度更新公式变为:

式中，c3为大于0的常数;r3为0～1之间的随机数。

(2)在粒子群每一次迭代过程中，首先给定一个设定值ε，如果粒子的第j维的速度Vij＜ε，则将此粒子第j维的速度在最大速度Vmax，j范围内重新初始化，从而提高粒子的全局搜索能力。若Vij＜ε，则:

式中，Vij为第i个粒子j维的速度;Vmax，j为第j维速度的最大值;rand为0～1之间的随机数。

(3)差异进化算法中粒子在每一次迭代过程中会出现差异信息。本文运用这一特点来提高粒子寻优能力。对满足式(14)条件的粒子进行差异进化变异，如下:

式中，P1j、P2j、P3j和P4j分别为在粒子的个体极值Pij中随机抽取的四个值;F取0.4。

可以看出，粒子群-差异进化混合算法在速度更新过程中不仅跟随粒子个体极值Pij和整体极值Pgj，还跟随第三值TVij和粒子群的差异信息，增加了粒子群的多样性，提高了算法整体搜索能力。由于算法引入了粒子的差异信息，使得算法开始以大步长寻优进行全局搜索;随着迭代的进行，粒子差异变小，每个粒子在自身范围内局部搜索，最终得到最优解。

4 利用粒子群-差异进化混合算法求解无功优化

4.1 控制变量的编码

无功优化的控制变量中，对连续变量采用实数编码，离散变量采用整数编码。其中发电机节点电压采用实数编码，补偿电容器投切组数和变压器分接头位置采用整数编码。混合编码方式如下:

式中，X为混合编码的粒子个体;VGi为第i个发电机的节点电压;Ti为第i个可调变压器的档位;Ci为第i个节点补偿电容器组数。

4.2 离散变量的处理

本文采用四舍五入归整法和映射编码法来处理离散变量。假设变压器的变比在范围内，调节步长为Tstep，对应第j维控制变量Xj，则令Xj的取值范围等于变压器变比范围，通过迭代更新后，进行转化计算:

式中，round对数据进行四舍五入。

对电容器投切组数处理依此法进行。

4.3 状态变量的处理

本文采取罚函数的方法处理状态变量。

4.4 算法流程

(1)输入系统数据及混合算法参数。

(2)计算粒子的适应度。

(3)按式(10)计算粒子的个体极值Pij和整体极值Pgj。

(4)判断是否满足变异条件，若满足，则按式(14)和式(15)进行变异。

(5)根据式(11)和式(13)更新粒子的速度和位置。

(6)判断是否满足终止条件，如果是，算法停止;否则返回步骤(2)。

5 算例分析

IEEE-30节点系统包含6台发电机、4台可调变压器以及2个容性无功补偿负荷节点［6］，接线图如图1所示，系统数据等参见文献［6］。本文采用粒子群-差异进化混合算法进行测试。系统参数均采用标幺值表示，基准功率设为100MVA。

图1 IEEE-30节点系统Fig.1IEEE-30 nodes system

优化前将各发电机节点电压和变压器变比设为1.0pu，各无功补偿容量设为0。发电机节点电压范围为0.9～1.1pu;变压器变比范围为0.9～1.1pu，步长为0.02pu;电容器补偿容量变化范围为0～0.05pu，变比步长为0.005pu;其他节点电压变化范围为0.9～1.1pu。

算法参数设置如下:粒子群规模N为50，粒子位置向量、搜索速度和最终优化解等皆为15维向量，终止优化的最大迭代次数K=100。优化后控制变量如表1所示，优化结果如表2所示。可以看出，粒子群-差异进化混合算法与遗传算法和粒子群优化算法相比，网损更小，网损下降率明显提高，收敛速度更快。

表1 优化后控制变量Tab.1Optimized control variables

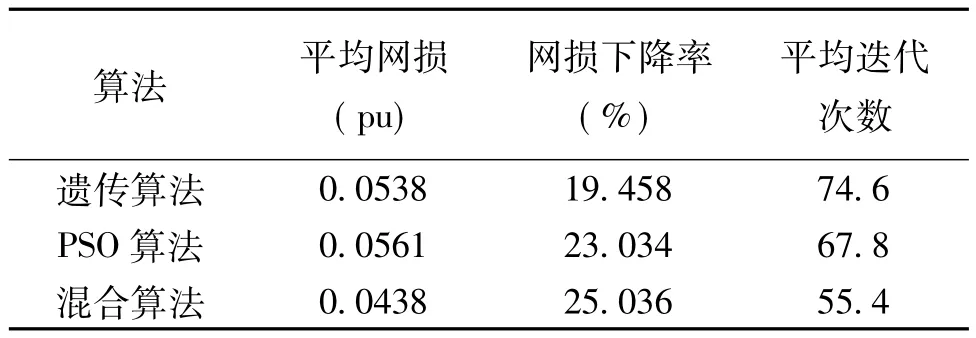
表2 不同算法的计算结果对比Tab.2Comparison of calculation results of different algorithms

优化前后节点电压对比如图2所示。可以看出优化后的节点电压均在约束范围之内，没有出现电压越限的情况，满足了用户需求。因此，本文提出的粒子群-差异进化混合算法应用于电力系统无功优化具有可行性和实用性。

图2 优化前后节点电压对比Fig.2Comparison of node voltage before and after optimization

6 结论

本文针对粒子群算法后期收敛速度慢且易于陷入局部最优等问题，提出了一种粒子群-差异进化算法，并将其应用到电力系统无功优化中。对IEEE-30节点系统进行计算并与遗传算法和粒子群算法比较，结果表明，本文算法寻优能力更好，能进一步降低系统网损，具有广阔的发展前景。

［1］刘宇，覃征，史哲文(Liu Yu，Tan Zheng，Shi Zhewen).简约粒子群优化算法(Contracted particle swarm optimization algorithm)［J］.西安交通大学学报(Journal of Xi’an Jiaotong University)，2009，3(40):184-190.

［2］张粒子，舒隽，林宪枢(Zhang Lizi，Shu Jun，Lin Xianshu).基于遗传算法的无功规划优化(Reactive power optimization based on genetic algorithm)［J］.中国电机工程学报(Proceedings of the CSEE)，2010，20 (6):5-8.

［3］J Kennedy，R Eberhart.Particle swarm optimization［A］.Proceedings of IEEE International Conference on Neural Networks［C］.1995.1942-1948.

［4］Wilson E O.Sociobiology:The news synthesis［M］.Cambridge MA:Belknap Press，2009.

［5］闻朝中，李智(Wen Chaozhong，Li Zhi).粒子群算法在配电网络无功优化中的应用(The application of particle swarm optimization in reactive power optimization in distribution network optimization compensation)［J］.武汉工业学院学报(Journal of Wuhan Polytechnic University)，2010，23(1):18-21.

［6］贾德香，唐国庆，韩净(Jia Dexiang，Tang Guoqing，Han Jing).基于改进模拟退火算法的电网无功优化(Reactive power optimization based on improved simulated annealing algorithm)［J］.继电器(Relay)，2004，32(4):32-35.

Reactive power optimization based on improved particle swarm optimization algorithm

ZHANG Yan，XU Wei-wei
(Control Science and Engineering College of Hebei University of Technology，Tianjin 300130，China)

This paper presents a particle swarm optimization-difference evolutionary algorithm that aims to solve the flaws of easy plunging into local optimum and it is applied for reactive power optimization.In the algorithm each particle keeps track of the third value which is created by the mutation operator of DE algorithm besides the best previous position found so far by itself and the best previous position among all particles.Besides，the velocity is

(，cont.on p.67)

(，cont.from p.51)reinitialized and the dimension of the personal best position is mutated by mutation operator of DE algorithm if the dimension of one particle’s veloeity of PSO algorithm is smaller than the specified value.Through the establishment of reactive power optimization mathematical model，the proposed algorithm optimizes IEEE 30-bus system through the Matlab programming，and compares with particle swarm optimization and genetic algorithm.The optimized results show that the proposed algorithm has better search capability and higher degree of convergence for reactive power optimization，and can control system according to the optimized results and hit the mark of decrease transmission loss and improve the quality of voltage level.

particle swarm optimization algorithm;difference evolutionary algorithm;reactive power optimization; voltage quality

TP29

A

1003-3076(2014)09-0048-04

2012-09-25

张燕(1974-)，女，河北籍，副教授，硕士研究生导师，博士，研究方向为模式识别与智能控制;许伟伟(1985-)，男，河北籍，硕士研究生，研究方向为模式识别与智能控制。