基于ABC-LSSVM的铝热连轧板凸度软测量建模
赵新秋, 刘正亮, 杨景明, 车海军
(1.国家冷轧板带装备及工艺工程技术研究中心,河北秦皇岛 066004;2.燕山大学工业计算机控制工程河北省重点实验室,河北秦皇岛 066004)
基于ABC-LSSVM的铝热连轧板凸度软测量建模
赵新秋1,2, 刘正亮1, 杨景明1,2, 车海军1
(1.国家冷轧板带装备及工艺工程技术研究中心,河北秦皇岛 066004;2.燕山大学工业计算机控制工程河北省重点实验室,河北秦皇岛 066004)
在铝热连轧板形控制中,板凸度是铝板带的重要指标之一。为了准确预测铝热连轧板凸度,提出了一种基于人工蜂群(ABC)和最小二乘支持向量机(LSSVM)的板凸度软测量模型。由于LSSVM的精度和泛化能力取决于模型参数的选择,故引入ABC进行参数优化。根据某厂1+4铝热轧现场采集的数据验证软测量模型的预测性能,并与GA-LSSVM模型和Marquardt模型做比较,仿真结果表明:建立的ABC-LSSVM板凸度软测量模型参数优化速度快、结构简单,并且具有较高精度。
计量学;板凸度;软测量;人工蜂群;最小二乘支持向量
1 引 言
随着铝产品需求的增加,铝加工产业生产规模逐渐扩大,而我国工艺设备水平与国际还有一段距离,改善铝板带质量成为迫切需要。铝热轧是一个非线性、多耦合、多变量的复杂系统,准确预测板凸度大小能够有效改善板形质量。而传统方法在估计板凸度时,存在许多假设条件简化了系统,降低了模型精度。软测量技术能够有效解决难于在线测量的过程质量指标估计问题,并在轧制过程中得到了普遍应用[1,2]。
最小二乘支持向量机算法是在支持向量机算法基础上的改进算法[3]。它基于小样本,实现了结构风险最小化,可以任意精度逼近非线性系统,是非线性系统建模的有力工具[4]。LSSVM模型中,核函数参数与最小二乘支持向量机中的惩罚参数ξ对模型精度有较大影响。目前,对于参数的常用优化方法包括:交叉验证方法、遗传算法和粒子群算法等。这些算法寻优效率低,易陷入局部最优,从而影响了整个模型的精度及泛化性能[5,6]。为此,利用人工蜂群算法对LSSVM参数优化,建立的软测量模型能够对铝热轧板凸度进行较好的估计。
2 板凸度影响因素

对于铝热轧,板凸度大小与很多因素有关,可表示为:式中,Fw为弯辊力,P为轧制力,b为板带宽度,CH为入口凸度,Cw、Cb分别为工作辊与支持辊的凸度,Dw、Db分别为工作辊与支持辊直径,l为辊长。
在传统方法中,根据物理模型分析工艺参数与板凸度之间的关系建立回归模型:
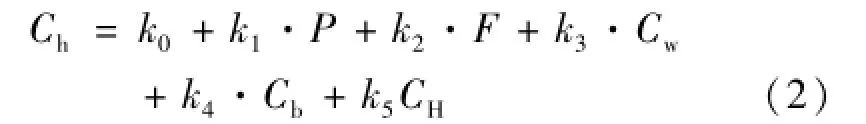
式中,k1~k5为影响系数,k0为常数项。根据新日铁提出的在线板凸度模型公式[7],模型可以写为:

式中,a1~a22为模型影响系数。
上述模型实现容易、速度快,较全面地考虑了轧制过程中的轧制因素,可以采用Marquardt法建立软测量模型。但由于在分析中采用假设简化和线性近似表示等措施,与设备状况、工艺条件复杂的现场情况有一定局限性。
3 最小二乘支持向量机
最小二乘支持向量机采用最小二乘线性系统作为损失函数,将不等式约束改为等式约束,求解过程变成了解一组等式方程,速度相对加快[8]。
优化问题:
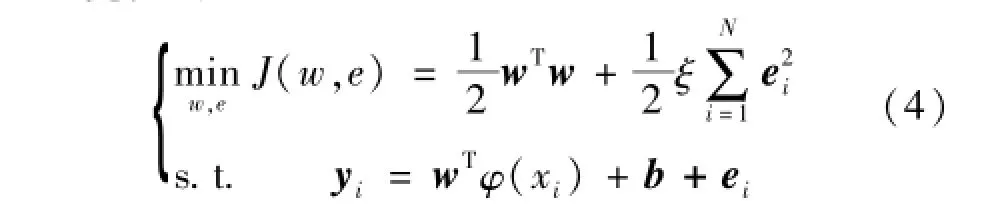

4 ABC优化LSSVM软测量模型
人工蜂群算法是模拟蜂群行为的一种新优化算法[9]。在ABC算法中,蜂群由采蜜蜂、跟随蜂、侦查蜂3种蜂构成。蜂群个体通过分工合作和信息传递获得最优解。食物源位置代表优化问题的可行解,花蜜量的多少代表适应度的大小。当某个食物源被采蜜蜂和跟随蜂舍弃时,这个食物源对应的寻蜜蜂就变为侦查蜂[10-11]。应用蜂群算法优化最小二乘支持向量机核函数参数σ2与惩罚参数ξ,优化步骤如下:

式中,objval为预测模型误差,m为训练样本数,yj为实际值,为模型预测值。
Step 2:采蜜蜂在可行解内搜索
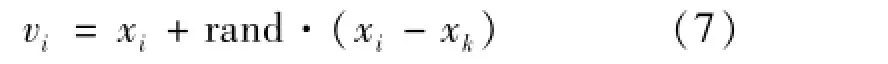
按照式(6)计算新的适应度NewFitness。若NewFitness>Fitness,则更新位置;否则个体失败次数LOST加1。计算每个个体的转换概率:

式中,fi为每个个体的适应度,个体的适应度越大,转换概率越大。
Step 3:采蜜蜂根据Pi转换为跟随蜂。跟随蜂进行一次搜索,若新的适应度值好于原解的适应度,则更新位置,否则失败次数LOST加1。
Step 4:判断个体更新失败次数LOST,若超过范围则抛弃成为侦查蜂,LOST清零,按照式(5)重新初始化。
Step5:若满足适应度允许条件或者达到迭代次数count则终止循环,输出结果。
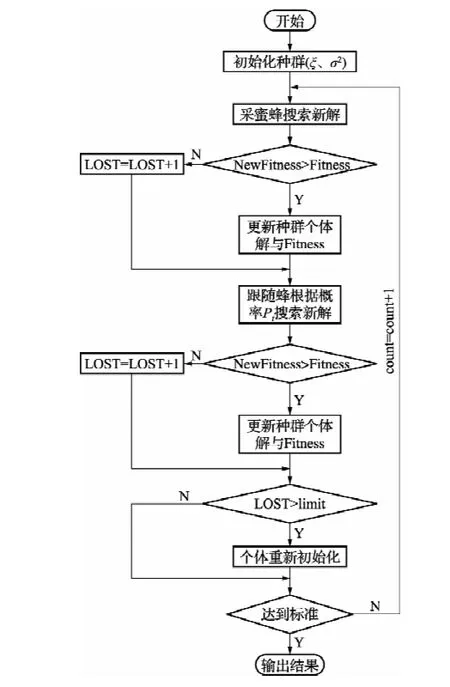
图1 LSSVM参数优化流程图
5 实验仿真与结果
本文研究对象为某铝厂1+4铝热连轧机组,分别抽取1系、3系和5系铝合金的现场数据,选择影响末机架板凸度的因素如材质、工作辊直径、温度、板宽、轧制力、压下量、弯辊力、入口凸度等为输入变量,出口凸度为输出变量,建立ABCLSSVM软测量模型。样本数据(共433组数据,随机抽取347组数据为训练样本,86组数据为测试样本)均进行了预处理,将误差较大的数据从样本集中剔除,并对数据进行归一化,转换为(0,1)范围内的变量。
为了验证模型的有效性,在建立ABC-LSSVM软测量模型的同时又建立了遗传最小二乘支持向量机(GA-LSSVM)和Marquardt软测量模型做实验对比。在matlab 7.6实验平台下,LSSVM参数搜索范围,ξ∈[0.01,1000];σ2∈[0.01,1 000];ABCLSSVM中种群数量20,被舍弃条件50。GA-LSSVM算法中种群大小为20,交叉概率pc=0.6,变异概率pm=0.1。
图2中显示了GA与ABC算法在模型参数寻优中适应度的变化曲线,可以看出,在整个阶段GA下降梯度明显比ABC收敛速度慢,GA迭代50次后达到最小值0.016 4,ABC在迭代10次后达到最小值0.015 62。蜂群算法在开始阶段适应度下降速度快,迭代3次以后逐渐趋于平缓,因此ABC算法的收敛性能优于GA。
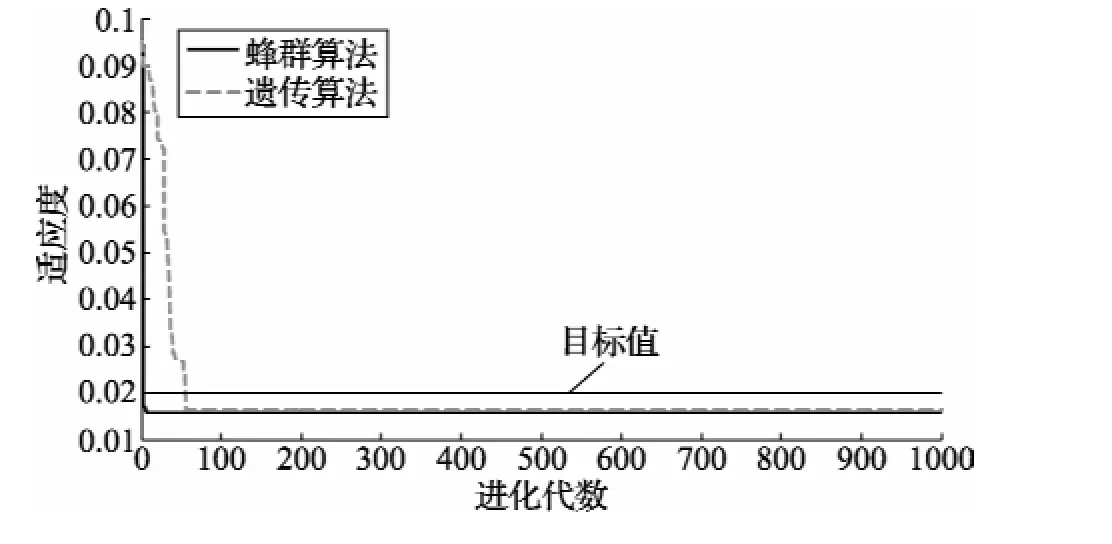
图2 GA与ABC寻优曲线图
ABC算法寻优后,LSSVM模型的最优参数σ2为0.013 7,ξ为246.369 9,代入LSSVM模型中,随机抽取347组数据进行训练和拟合,拟合结果如图3。从图3中可以看出,ABC-LSSVM模型对数据能够很好地拟合。将剩余86组样本数据进行数据预测,预测结果如图4。从图4中可以看出,ABCLSSVM能够较好地预报测试数据。

图3 ABC-LSSVM软测量模型拟合曲线图

图4 ABC-LSSVM模型预测曲线图
为了评价ABC-LSSVM模型的预测性能,表1分别列出了各个模型的均方根误差。在训练样本中可以看出,Marquardt软测量模型均方根误差远远大于GA-LSSVM与ABC-LSSVM软测量模型,ABCLSSVM均方根误差最小。因而,ABC-LSSVM模型的拟合性能较高。在测试样本中可以看出,ABCLSSVM软测量模型的均方根误差小于其他两种模型,泛化能力较好。结合训练样本和测试样本,GALSSVM软测量模型虽然拟合较好,但是泛化能力较弱。

表1 Marquardt、GA-LSSVM和ABC-LSSVM预测结果均方差对比
综上所述,本文建立的ABC-LSSVM铝热轧板凸度软测量模型泛化能力强、预测精度高。
6 结 论
在分析板凸度相关因素基础上,本文提出了一种ABC-LSSVM铝热轧板凸度软测量模型。将ABC与LSSVM相结合实现优势互补,以大量现场数据进行仿真实验,验证软测量模型的有效性。将该模型与PSO-LSSVM、Marquardt进行对比,结果表明,ABC-LSSVM软测量模型能够较好地预测板凸度,为提高板形质量提供了又一种新方法。
[1] 王伟,陈殿生,魏洪兴,等.装载机载重测量的支持向量机软测量建模方法[J].计量学报,2008,29(4):329-333.
[2] 胡伟.基于反馈BP网络的铝热连轧板凸度预报建模[J].计算机与现代化,2011,(11):11-14.
[3] 吴德会.基于最小二乘支持向量机的传感器非线性动态系统辨识[J].计量学报,2008,29(3):226-230.
[4] 顾燕萍,赵文杰,吴占松.最小二乘支持向量机的算法研究[J].清华大学学报(自然科学版),2010,50(7):1063-1066.
[5] 李文莉,李郁侠.基于粒子群最小二乘支持向量机的水文预测[J].计算机应用,2012,32(4):1180-1190.
[6] 周辉仁,郑丕谔.基于GA和Bootstrap的最小二乘支持向量机参数优选[J].系统仿真学报,2008,20(12):3293-3296.
[7] Johan V R,Hedwig V,Rainer M.Accurate profile and flatness control on a modernized hot strip mill[J].Iron and Steel Engineer,1996,73(2):29-33.
[8] Deng S,Tsung-Han Yeh.Applying least squares support vectormachines to the airframe wing-box structural design cost estimation[J].Expert Systems with Applications,2010,37(12):8417-8423.
[9] Karaboga D,Basturk B.A powerful and efficient algorithm for numerical function optimization:artificial bee colony(ABC)algorithm[J].Journal of Global Optimization,2007,39(3):459-471.
[10] 曹文平,李伟华,王利鑫,等.人工蜂群算法在飞轮充电控制系统中的应用研究[J].华东电力,2011,39(9):1500-1504.
[11] 于明,艾月乔.基于人工蜂群算法的支持向量机参数优化及应用[J].光电子·激光,2012,23(2):374-378.
The Alum inum Hot Strip M ill Plate Crown Soft Sensor Modeling Based on the ABC-LSSVM
ZHAO Xin-qiu1,2, LIU Zheng-liang1, YANG Jing-ming1,2, CHE Hai-jun1
(1.National Engineering Research Center for Equipment and Technology of Cold Strip Rolling,Qinhuangdao,Hebei066004,China;
2.Key Lab of Industrial Computer Control Engineering of Hebei Province,Yanshan University,Qinhuangdao,Hebei066004,China)
The plate crown is an important indicator of the aluminum strip in Aluminum hot strip mill flatness control. In order to accurately predict the alum inum hot strip mill plate crown,a soft sensor model was established on the base of artificial bee colony(ABC)and least squares support vectormachine(LSSVM).ABC was applied to the process of the model parameters optimization because prediction accuracy and generalization ability of LSSVM model depends on the choice of the parameters.The prediction performance of the model was tested by sample data collected at the scene of a factory 1+4 aluminum hot rolling.Themodelwas compared with Marquardtand the LSSVM modelwhose parameterswere optimized by Genetic Algorithms(GA).The simulation result shows that the ABC-LSSVM soft sensor model parameters optim ization fast,simple structure and high precision.
Metrology;Plate crown;Soft sensor;Artificial bee colony;Least squares support vectormachine
TB921
A
1000-1158(2014)04-0323-04
10.3969/j.issn.1000-1158.2014.04.04
2012-11-14;
2013-07-23
河北省科技支撑计划项目(10212157);国家冷轧板带及装备工程技术研究中心开放课题;河北省工业计算机控制工程重点实验室开放课题
赵新秋(1969-),女,吉林辽源人,燕山大学副教授,博士,主要从事冶金自动化方面的研究。zxq5460@ysu.edu.cn

