基于FPGA的逐次逼近算法实现激光干涉信号细分
黄晓清, 高思田, 缪 琦, 卢荣胜
(1.合肥工业大学仪器科学与光电工程学院,安徽合肥 230009;
2.中国计量科学研究院,北京 100029)
基于FPGA的逐次逼近算法实现激光干涉信号细分
黄晓清1, 高思田2, 缪 琦1, 卢荣胜1
(1.合肥工业大学仪器科学与光电工程学院,安徽合肥 230009;
2.中国计量科学研究院,北京 100029)
为了实现激光干涉测量中信号的高速度、高精度细分,对正切细分算法中的除法运算进行了改进,采用逐次逼近算法替代使用较多的移位相减算法。实验证明逐次逼近算法比移位相减算法运算速度更快、资源占用较少。更适合FPGA信号细分高速度、高精度要求。
计量学;细分;激光干涉;逐次逼近;移位相减;FPGA
1 引 言
高精度几何尺寸测量仪器常基于激光干涉原理[1,2]。而激光干涉的信号处理流程一般有3步。首先,激光干涉输出的两路或者四路信号经过光电转换[3]。其次,利用A/D对多路信号采集并将模拟信号转换为数字信号。最后,再由微处理器或者逻辑电路对信号进行运算和查表得到位移值。
图1是激光干涉信号处理流程图。目前,提高激光干涉仪分辨率的方法主要有两种:光学倍程法和电子细分法[4,5]。然而光学细分倍数增大使得反射次数和反射面增多,导致光强损失严重,光的偏振态也会产生不应有的变化,对光学元件的镀膜要求很严格[6]。

图1 激光干涉信号处理流程图
根据电子细分采用的算法不同,最常用的细分方法主要有正切量化细分法、三角波细分法、正余弦结合细分法、正弦量化细分法[7]。由于正切量化细分法对光强变化不敏感,利于信号处理,是4种算法最常用的,该算法中除法运算是最关键的,其运算的复杂程度直接影响信号细分处理的速度。现有的细分方法中除法运算无论在微处理器还是逻辑电路中都很复杂,而且耗时较多,影响着整个信号处理过程的速度。本文基于此方法研究了一种逐次逼近算法,原理较简单、步骤较少、耗时较短,对信号处理速度有很大提高。
2 细分算法
2.1 正切量化细分法
正切量化细分法的原理是将相互正交的正余弦信号同时进行A/D转换。转换得到的数字信号进行除法运算求出正切值,然后通过计算反正切或者查表获得相应的相位值,该相位值与一个信号周期内的位移台的位置一一对应。
在正切量化细分中,关键是采用除法运算,可以将干涉光信号sinθ和cosθ直接进行内存的二维地址寻址变为一维的tanθ寻址;其次tanθ的线性度好有利于制作细分表;最后除法运算可以消除信号光强的变化引起的误差[8]。根据激光干涉仪输出的正余弦信号u1=Asinθ、u2=Acosθ,由式(1)和式(2),就能得到|tanθ|和|cotθ|,如图2所示。


图2 正切余切图
根据图2的sinθ和cosθ信号的正负和绝对值大小的比较可以分出8个区间(见表1),这是因为在某些RAM或ROM比较小的现场可编程门阵列(FPGA),如果再加上表格细分倍数较大,数据量多,那么只需要建立一个区间或者两个区间进行查表(如果8个区间非常相似且线性度非常好的话,可以这样做),但是一般情况下,认为误差在一个整周期2π空间内是完整的。
若整个区间要实现2 048次细分,细分数均分到1/8区间是256次细分,故只需要输入8位,就能在0-FF之中实现256细分。对于A/D的精度要求很低,而对于A/D的信号质量以及稳定性很高。若在光路上实现4倍程或者8倍程,又或者在电路上实现硬件细分,就能达到非常高的细分精度。
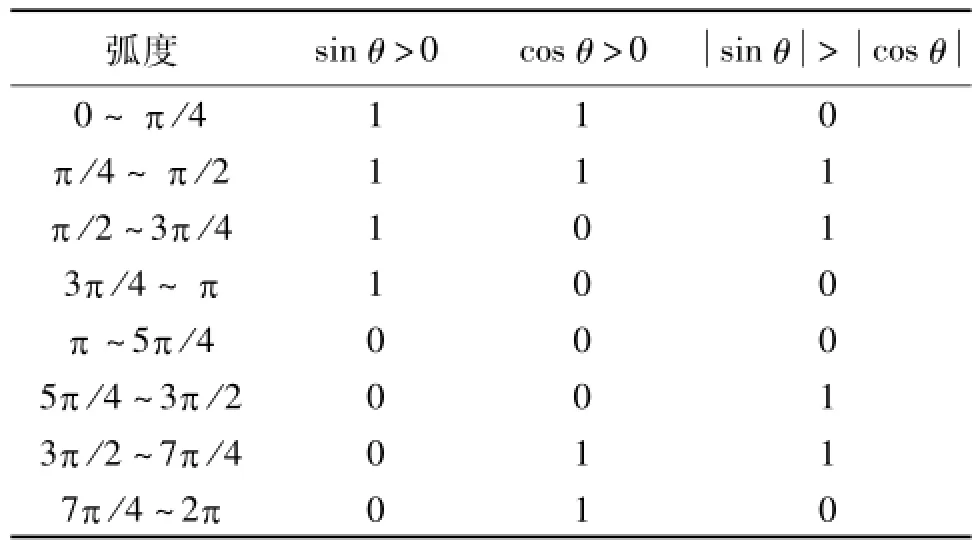
表1 8个区间细分表
基于FPGA的正切量化细分算法的关键是除法,运算一般使用除法IP核或使用移位相减算法,下面将介绍一种逐次逼近算法。
2.2 逐次逼近算法
图3是逐次逼近算法流程图,以A、B两个数相除得到一个10位二进制数的商为实例。

图3 逐次逼近算法流程图
具体步骤如下:首先这种算法主要是针对小数B除以大数A,商在0-1之间,所以结果只有小数部分,对大数A进行除以2、4、8、16、32、…、1 024运算(也就是大数A的二进制数右移1、2、3、…、10位,本次示例采用10 bits精度),然后分别按以下方式比较大小并确定相应位的二进制数。
(1)A/2跟B的大小来确定D[9](D的小数点后最高位)的值,B大则D[9]为1;B小则D[9]为0;若相等,则D[9]为1,D[8∶0]=0。
(2)D[8](D小数点后第二位)的确定由前一步来决定(假设第一步B比A/2大)。这时候应该比较(A/4+A/2)和B的大小,若B小D[8]为0;若B大则D[8]为1;若相等D[8]为1,D[7∶0]=0。
(3)D[7]小数点后的第三位的确定先前两步来决定哪两个数和B比较大小,类似于第二步,直到最后一位D[0],这样计算下来,就得到了D[9∶0]值,也就是B/A,余数是B-C。
这个算法的特点是运算前把需要的数据先准备好(对大数右移),然后就是相加,比较大小,确定每位小数位数。这个左移或者右移操作可以让硬件乘法器来操作,可以充分利用FPGA中内部资源,并且还能增加运算速度。对于一般的信号处理是不错的算法,而且该算法的精度是可调控制的。这个算法只是将两路信号SIN和COS相除,能够对系统误差有效地抑制。图4是算法的仿真情况。
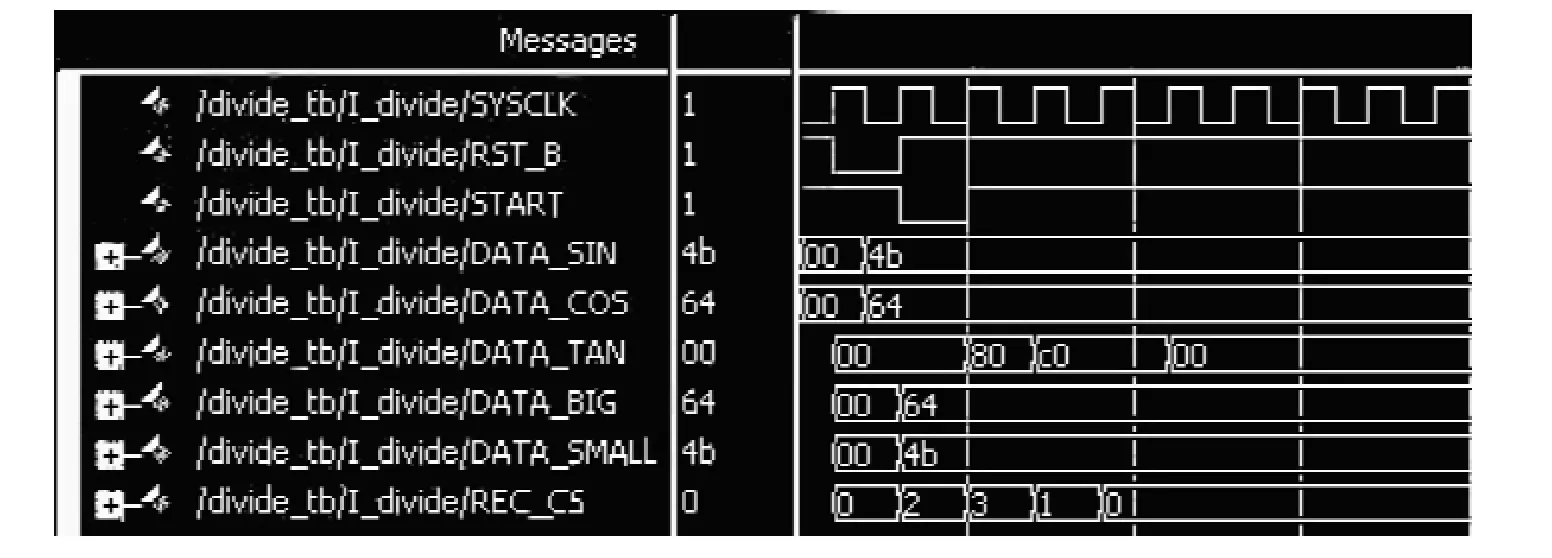
图4 逐次逼近算法模块的modelsim仿真
输入的数据为DATA_SIN=4b(75)和DATA_ COS==64(100),小数除以大数得到的肯定在0到1范围内,DATA_TAN为除法结果(结果只包含小数部分)=0.C0(十六进制)=0.1100_0000(二进制)=0.75(十进制)。从图4看到,在START变为低电平开始,到结果DATA_TAN输出所用时间为2个时钟周期,根据输入的数据的不同,这算法耗时有长有短,但是可以假设各种数据出现的概率一样,那么算法的平均耗时是可以得到的,假设要实现精度为8bits的除法,平均耗费将为4个时钟周期。若精度16bits,平均耗时为8个时钟周期。逐次逼近式算法的资源占用情况如下。
2.3 移位相减算法

图5 移位相减算法流程图
图5是定点型移位相减算法流程图。输入的A与B是假设为16 bit数字信号,保证每次相除时总是A≤B(A为被除数,B为除数),这样保证结果分布在0~1区间。每次A右移一位,A即增大2倍,A与B相减,得到的余数输入到A。如果A≥B,则C对应的位为1,相减的余数就是A-B;如果A<B,则C对应的位为0,相减的余数是A。而相减的余数赋给A,然后A继续右移一位,A和B相减,循环相减loop次[9]。右移相减次数越多,精度越高,并保证右移的次数就是除法的精度位数。
移位相减法modelsin仿真情况见图6,输入的数据为DATA_BIG=4b(75)和DATA_SMALL==64(100),小数除以大数得到的肯定在0到1范围内(结果全只包含小数部分),RESULT为除法结果=0.300(十六进制)=0.11_0000_0000(二进制)=0.75(十进制)。从图6看出,在SHIFT_EN变低以及LATENCH变高开始,到RESULT输出结果耗费了5个时钟周期,假设要实现该算法的精度为8bits,平均耗费7个时钟周期。若精度16 bits,平均耗时也就11个时钟周期。下面是移位相减算法的资源占用情况。
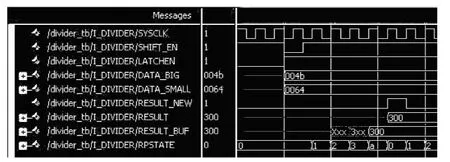
图6 移位相减算法modelsim仿真

3 结 论
根据逐次逼近算法和移位相减算法的资源占用情况、算法速度、算法精度的比较,算法优劣情况如下:
(1)资源占用比较。由于移位相减算法的步骤比逐次逼近算法的步骤要多,而且使用的变量也多很多,所以移位相减算法要占用更多的专用的逻辑寄存器。再从图5和图8对比就可以看出,移位相减算法的使用逻辑寄存器是逐次逼近式算法的4倍还多。LE单元两种算法使用的数量基本一样。这就证明逐次逼近算法要比移位相减算法更节省资源。
(2)算法速度比较。这两种算法的耗时都不是固定的。根据输入的数据不同,得到结果的步骤不一样,使用的时间自然不同,平均使用的时钟就减少了,从而达到提高运算速度的要求。首先从流程图可以看出,移位相减算法的步骤要多一些;其次根据算法原理,逐次逼近算法流程步骤是先将数据准备好之后(这种处理可以充分使用硬件乘法器),再进行比较、相加、再比较。移位相减算法流程步骤却是比较、相减、移位、赋值、再比较,整个流程前后相互依赖,所以相对逐次逼近算法要复杂;最后对比图3和图6,发现移位相减算法用来了5个时钟周期,而逐次逼近式算法只用了3个时钟周期,明显比移位相减算法要快。
(3)算法精度比较。两种算法的精度没有明显的区别,只要循环次数更多,用时更长,精度都能达到很高,故速度和精度的取舍就需要具体情况具体分析。
[1] 郁道银,谈恒英.工程光学[M].北京:机械工业出版社,2006,306-323.
[2] Wang Q,Chen J.Interferometric system used for testing microdisplacement automatically[J].Nanjing Li Gong Daxue Xuebao/Journal of Nanjing University of Science&Technology,1998,22(2):145-148.
[3] 吕立宁.FPGA在相位激光测距信号处理技术中的应用[D].武汉:华中科技大学,2005.
[4] 赵美蓉,曲兴华,陆伯印.光程差倍增的纳米级精度激光干涉仪[J].中国激光,2000,5,27(5):431-434.
[5] 王维东.高精度光栅信号处理方法研究[D].合肥:合肥工业大学,2012.
[6] 孙长库,叶声华.激光测量技术[M].天津:天津大学出版社,2001:37-45.
[7] 陈曦.数字集成的莫尔条纹信号细分原理及应用[D].沈阳:沈阳工业大学,2009.
[8] 来展,邵宏伟,高思田,等.激光干涉仪误差修正系统的设计[J].计量学报,2010,31(z2):135-138.
[9] 来展.激光干涉仪信号处理系统及纳米测量机控制系统的研究[D].北京:中国计量科学研究院,2011.
Successive Approxim ation Division Algorithm in Laser Interference Signal Subdivision Based on FPGA
HUANG Xiao-qing1, GAO Si-tian2, MIAO Qi1, LU Rong-sheng1
(1.Hefei University of Technology,Hefei,Anhui230009,China;
2.National Institute of Metrology,Beijing 100029,China)
In order to achieve the goal of the laser interferencemeasurement signal being in high speed and high precision subdivision,the division of tangent subdivision algorithm is improved.The successive approximation algorithm instead of using shift subtraction algorithm is used more in the past.Experiments prove that successive approximation algorithm is faster than shift subtractionm,resource usage is less,and successive approximation algorithm ismore suitable for FPGA based on high speed and high precision requirements.
Metrology;Subdivision;Laser interference;Successive approximation;Shift subtraction;FPGA
TB92
A
1000-1158(2014)04-0311-04
10.3969/j.issn.1000-1158.2014.04.02
2013-08-07;
2014-02-18
国家自然科学基金(91023021)
黄晓清(1989-),男,江西吉安人,合肥工业大学硕士研究生,研究方向为仪器科学与光电测试技术。huangxq@nim.ac.cn高思田为通讯作者。gaost@nim.ac.cn

