承载围岩渗透率演化模型及数值分析

于永江,张春会,赵全胜,王来贵

(1.辽宁工程技术大学矿业学院,辽宁阜新 123000;2.河北科技大学建筑工程学院,河北石家庄 050018)

承载围岩渗透率演化模型及数值分析

于永江1,张春会2,赵全胜2,王来贵1

(1.辽宁工程技术大学矿业学院,辽宁阜新 123000;2.河北科技大学建筑工程学院,河北石家庄 050018)

为反映承载围岩变形破坏过程中渗透率的变化,将岩石变形破坏过程视作弹-脆-塑过程,分析了岩石全程应力-应变-渗透率关系,建立岩石渗透率演化数学模型。模型中岩石单元的渗透率演化包括如下阶段:①岩石单元破坏前,渗透率为孔隙率的函数;②若岩石单元发生剪切破坏,假设岩石单元剪胀扩容在单元体内引起两条斜交裂隙;③若岩石单元发生拉破坏,体积膨胀在单元体内引起两条正交的裂隙。基于平行板的渗透率立方体定律计算破坏岩石单元的渗透率,进而建立了承载岩石弹性变形、脆性破坏全过程的岩石渗透率演化模型。在FLAC软件下利用Fish函数方法实现了该模型。数值算例研究了不同围压下加载立方体岩样的渗透率演化过程,结果表明:建立的模型可以较合理地反映承载岩石弹性变形和破坏引起的渗透率变化,也可以较合理地反映围压对岩石渗透率的影响。

承载围岩;渗透率;围压;剪胀;拉破坏

Key words:load rock;permeability;confined stress;dilation;tension failure

岩石的渗透率是表征岩石渗透性能的主要参数,通常受应力、温度、孔隙及裂隙空间多少等因素的影响,并随着这些因素的改变而改变。描述渗透率与这些因素之间关系的数学表达式就是渗透率模型[1-5]。岩石渗透率模型一直是煤层瓦斯抽放、核废料处置[6-7]、CO2地下封存[8]等工程设计和计算分析的关键。目前在岩石工程中广泛使用Louis公式、仵彦清公式、赵阳升公式、Klinbenberg公式等来描述应力及孔压对岩石渗透率的影响[1-8],这些公式较好描述了岩石破坏前应力及孔压对渗透率的影响。然而,在岩石工程中围岩局部破坏现象普遍存在,破坏岩石的渗透性与破坏前相比发生了很大变化,并可能引起采动围岩各种灾变如突透水、岩爆等。因此,预测承载岩石变形破坏全过程中渗透率的演化已成为岩石工程计算分析中一个关键。近些年,一些学者已开始关注破坏岩石的渗透性变化[9-11],但总体上岩石变形破坏全过程的渗透率定量预测尚不完善。

本文在已有实验研究基础上,提出了一个渗透率模型,并开发了相应的数值计算程序。

1 岩石应力-变形-渗透率的关系

已有三轴渗流实验研究表明,岩石的渗透率与岩石的变形过程及破坏密切相关。岩石变形通常可简化为4个阶段,即线弹性变形阶段、应变硬化阶段、峰值强度(破坏阶段)及峰后应变软化阶段。在线弹性阶段,随着轴向应力增加,岩石压缩,其内的孔隙和裂隙空间减少,渗透率降低。当荷载达到屈服应力进入应变硬化阶段时,岩石内部出现裂隙扩展,并产生新裂隙,体积应变增长速率趋缓(压缩为正),甚至出现负增长(即体积膨胀),相应的岩样的渗透率减小速率趋缓,甚至渗透率开始增长。当轴向应力达到峰值强度附近时,岩石体积膨胀更加明显,渗透率也更显著增加,具体如图1所示。

图1 全程应力-应变-渗透率曲线Fig.1 Curves for stress-strain-permeability

岩石的屈服应力通常约为峰值应力的1/2～2/ 3,岩石的应变硬化阶段通常并不长,若采用线弹性代替,对力学分析影响不大。在应变硬化阶段,岩样的渗透率有所改变,但在达到峰值强度前,基本上属于过渡阶段。为简化分析用线弹性代替应变硬化阶段。

在峰值强度后,岩石发生破坏,承载能力下降,进入应变软化阶段,同时发生剪胀扩容,渗透率增长。为简化分析,假设岩石峰值强度后应力发生脆性跌落,降至残余强度后保持不变,则岩石的全程应力-应变-渗透率简化为如图2所示。

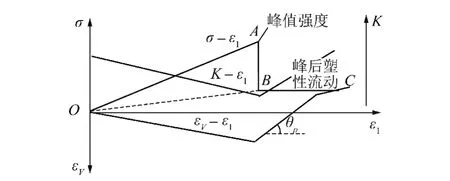
图2 全程应力-应变-渗透率简化曲线Fig.2 Simplied curves for stress-strain-permeability

由图2将岩石视作弹脆塑材料,其变形破坏包括:① 线弹性变形阶段(OA段);② 脆性跌落阶段(AB段);③峰后理想塑性变形阶段(BC段)。

与变形破坏过程相对应岩石的渗透率变化过程包括:①线弹性变形阶段,岩石体积压缩,岩石的渗透率减小;②应力达到峰值后,岩石发生破坏和剪胀扩容,渗透率增加;③ 若岩石承受拉应力,在拉破坏前岩石体积膨胀,岩石渗透率增大,若岩石发生拉破坏,岩石内出现拉裂隙,渗透率显著增加。

2 围岩变形破坏的力学模型

2.1 围岩变形破坏弹脆塑力学模型

将岩石视作弹脆塑材料,其变形破坏过程简化后包括:线弹性阶段、脆性跌落阶段和峰后理想塑性变形阶段,如图2所示。

采用Mohr-Column准则判别岩石单元是否发生破坏:

式中,σ1为最大主应力;σ3为最小主应力;k=(1+ sin φ)/(1-sin φ),φ为内摩擦角;σc0为单轴抗压强度。

岩石脆性跌落后的残余强度和剪胀量都与围压有关。研究表明[12-13],随着围压增加,岩石的塑性增加,脆性减弱,峰后残余强度降减小,剪胀性减弱。当围压达到“脆延转化”围压,岩样变形近似呈现理想塑性,岩样剪胀扩容也基本消失。

围压对岩石残余强度、残余弹性模量和剪胀扩容特性的影响可利用强度退化指数和剪胀扩容指数[14]来表示。

强度退化指数可以表示为

式中,δσp,δEp分别为围压σ3时的强度和弹性模量的退化值;δσ0,δE0分别为单轴条件下强度和弹性模量的退化值。

于是岩石破坏后的残余模量和残余强度可以分别表示为

式中,E0和σc分别为峰前弹性模量和强度。扩容指数可以表示为

其中,θp为图2所示围压为p时的岩石破坏后体积应变与轴向应变的夹角;θ0为围压为0时的岩石破坏后体积应变与轴向应变的夹角;ΔεVp和Δε1p分别为塑性体积应变增量和塑性轴向应变增量。根据试验资料[12-13],对于单轴条件Id=1,当围压较高时,由于围压的约束,基本没有扩容,这时Id=0。

于是剪胀角可以表示为

围压与退化指数和扩容指数的关系可分别表示为

其中,β为拟合常数,大于0;σh为无剪胀时的围压值;md为试验参数。单轴条件下χσ=1,随着围压增大,χσ呈负指数减小。当围压达到“脆延转化”围压,岩样变形近似呈现理想塑性,这时χσ近乎为0。

2.2 力学参数

模型中弹性模量、泊松比、内摩擦角、黏聚力、峰后弹性模量、单轴条件下的强度降、剪胀角、β, σh,md,θ0都可通过岩石三轴实验确定,峰后残余内摩擦角、残余黏聚力则通过Hoek-Brown屈服准则和Mohr-Column屈服准则之间的参数转换关系确定,其表达式为

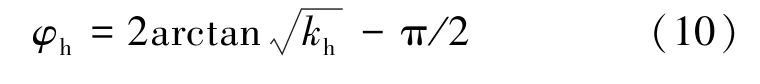
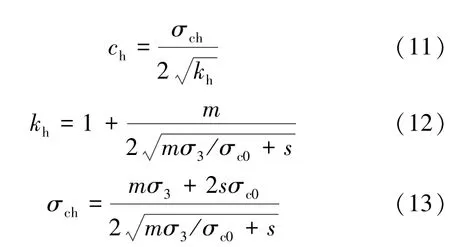
式中,m,s为Hoek-Brown准则参数;σc0为单轴抗压强度;φh和ch分别为用Hoek-Brown参数表达的Mohr-Column等效内摩擦角和黏聚力。

Hoek-Brown准则参数m和s可分别表示为

式中,mi为完整岩石的Hoek-Brown参数m,对于完整岩石,s=1,则

其中,T0为岩石单轴抗拉强度。

利用式(4)计算岩石单元的残余强度,利用式(14),(15)计算峰后的Hoek-Brown准则参数m和s,再利用式(10)～(13)计算岩石单元峰后残余内摩擦角和残余黏聚力。

3 渗透率演化模型

岩石的渗透率本质上是由岩石的孔隙和裂隙空间增减决定的,因此可以利用变形来描述岩石的渗透率变化规律。岩石的变形包括剪切变形和体积胀缩,并可分别用剪切应变和体积应变来描述。剪切应变描述了岩石单元体形状的改变,这种变形不改变岩石单元体的孔隙或裂隙空间大小,但单元体受剪力作用,固体颗粒之间会发生剪切变形甚至错动(破坏),从而改变岩石单元体内部的孔隙连通,这对岩石单元体的渗透性能有一定影响。体积应变描述了岩石单元体的体积变化,由于岩石单元体固体颗粒变形微小,单元体的体积变化主要是孔隙或裂隙空间的改变。为此,可假设岩石单元体渗透率变化主要取决于单元体体积的胀缩及是否发生破坏。

依据前述岩石应力-变形-渗透率之间的关系,可以建立基于体积应变和破坏的岩石单元体渗透率演化模型,并简化成如图3所示。

(1)图3(a)中AB段为三轴压缩岩石线弹性阶段,图3(b)中DE为三轴拉伸岩石线弹性阶段。

在弹性变形阶段(图3(a)中AB和图3(b)中DE段),岩石单元体的渗透率[14]可表示为

图3 岩石单元的渗透率与体积应变之间的关系Fig.3 Relationship between permeability and volumetric strain for rock element

式中,k0为无应力煤岩的渗透率;γ为试验拟合参数; φ0,φ分别为无应力时岩石单元体的孔隙度和某应力下的孔隙度。

结合有效应力原理,体积应变可以写为

式中,K为岩石体积模量;σ-为平均应力;p为孔隙流体压力;α为Biot系数,α=1-K/Ks,Ks为岩石体积压缩系数,MPa-1。

若岩石单元的孔隙体积Vp,固体颗粒体积为Vs,则总体积为V=Vp+Vs。岩石单元体的孔隙度表示为φ=Vp/V。单元体的体积应变和孔隙空间的体积应变可分别表示为

式中,Kp为孔隙的体积模量;β=1-Kp/Ks。

由Betti-Maxwell理论,有

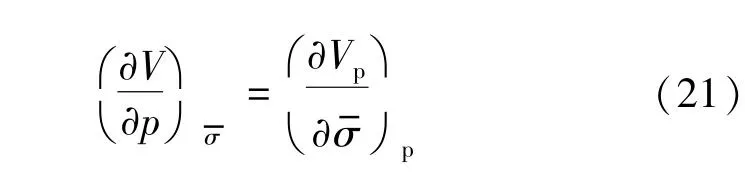
进而可以得到

由孔隙度的定义可以得到

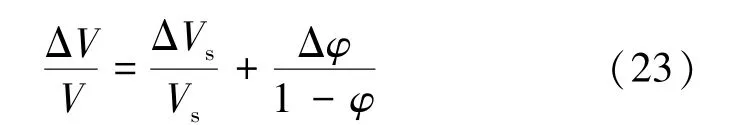
式(29)为岩石单元线弹性变形阶段的渗透率演化方程。

(2)若岩石单元发生剪切破坏,则假设在单元内出现共轭剪切带,剪切带与最大主应力夹角为45°+ φ/2,剪切带宽度为Δe,按照图3若体积膨胀应变为εV(以最大压缩时为基准计算),若单元尺寸为l(按平面应变推导,正方形单元,如图3所示),则

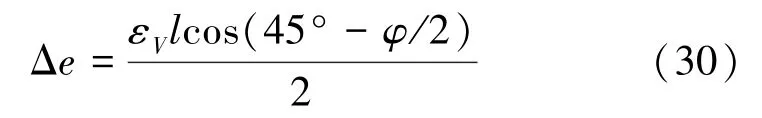
由平行板立方体定律可以得到裂隙形成时的单元渗透率为

式中,Δe为裂隙宽度;μ为流体动力黏度;g为重力加速度。

(3)若单元发生拉破坏(图3(b)),假设在单元体内形成正交的两条裂隙,裂隙宽度可以表示为

式(29),(31)和(33)就是岩石变形破坏全过程的渗透率计算模型。

同样由平板立方体定律得到单元体渗透率为

4 岩石的非均质描述方法

岩石是一种非均质材料,其非均质力学特征可以用Weibull分布模拟,其分布函数[1]为

式中,mw为非均质程度系数;xu为x的下限值;x0为x的统计均值;x为力学参数,如弹性模量、单轴抗压强度、抗拉强度等。

式(34)中Weibull分布参数mw,x0,xu可利用岩样的大量实验数据通过统计拟合方法获得。

5 数值实现

线弹性变形阶段的本构方程可以表示为

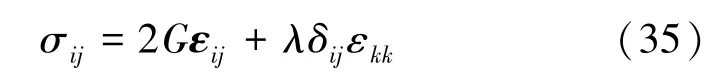
式中,G为剪切模量;λ为拉梅常数;δij为Kronecher符号;εij为应变张量;εkk为第1应变不变量。

脆性跌落发生由Mohr-Column准则用式(1)判断。发生脆性跌落后,岩石可视作由峰后模量、峰后内摩擦角和黏聚力为力学参数的理想弹塑性材料,其应力增量和应变增量之间的关系可以表示为

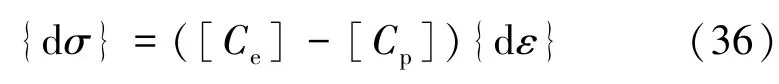
式中,[Cp]为塑性矩阵,可以表示为

式中,F为屈服函数,取式(1)形式;G为塑性势函数,取式(1)形式,但用剪胀角代替摩擦角。

基于以上,利用FLAC软件Fish函数方法实现本文渗透率演化模拟分析的计算过程为:

(1)建立计算分析模型,进行网格剖分。

(2)基于Weibull分布为每一单元赋值力学参数,如弹性模量、单轴抗压强度等,并写成“input.data”。

(3)将岩石视作 Mohr-Column材料,从“input.data”内读入岩石的弹性模量、单轴抗压强度σc0、泊松比、抗拉强度T0、岩体质量参数s、强度和刚度退化指数参数χσ、扩容指数参数md和σh、单轴下强度和刚度的最大退化值、单轴下的岩石剪胀角、Biot系数、峰前渗透率系数、无应力岩石孔隙度和渗透率、流体动力黏滞系数等。

(4)施加初边值条件,计算初始应力状态。

(5)对每一个单元根据其围压计算峰前力学参数,并为其赋值。

(6)施加第1步荷载,先按弹性进行单元应力及应变计算分析,然后对每一个单元利用Mohr-Column准则判断其是否发生破坏。

(7)若单元未发生破坏,仍保持峰前力学参数不变,并按式(29)计算单元的渗透率。

若单元发生破坏,发生脆性跌落,计算峰后力学参数,并赋值该单元,而后材料参数仅随应力水平做调整,渗透率按式(31),(33)计算。

(8)施加下一步荷载,反复重复上述过程,直至计算结束。

基于上述过程,在FLAC中利用Fish函数方法实现了本文模型。

6 数值算例

数值算例研究一立方体岩样不同围压下三轴加载渗透率的演化过程。岩样尺寸为0.05 m×0.05 m× 0.1 m,共划分30×3×60个网格。边界条件为z方向加载,加载速度为0.25 μm/step,侧向施加不同围压,分别为0,5 MPa。岩样的物理力学参数见表1。

设置流体压力为0(即不考虑流体的作用),以集中考虑应变及剪胀扩容对渗透率的影响。

利用所建立的数值模型进行计算,所获得的轴向应力和轴向位移曲线如图4所示。从图4可以看出,随着围压增加,岩样的强度降逐渐减小。

图5是2种围压下岩样的轴向位移和体积应变关系曲线。从图5可以看出,在加载初期,岩样发生弹性压缩,体积应变为压缩,岩样的体积减小,渗透率降低。当应力达到峰值强度时,岩样发生剪切破裂,剪切面上颗粒之间发生相对滑动,岩样的孔隙或裂隙空间增加,出现剪胀扩容现象。对比图5中0和5 MPa的体积应变和轴向应变关系曲线可见,围压对岩样的剪胀扩容有很大影响。随着围压增加,岩样的剪胀扩容速率变缓。

表1 岩样的物理力学参数Table 1 Physical and mechanical parameters for rock sample

图4 不同围压下试样轴向位移-轴向应力曲线Fig.4 Axial displacement and stress curves under varied confining stress

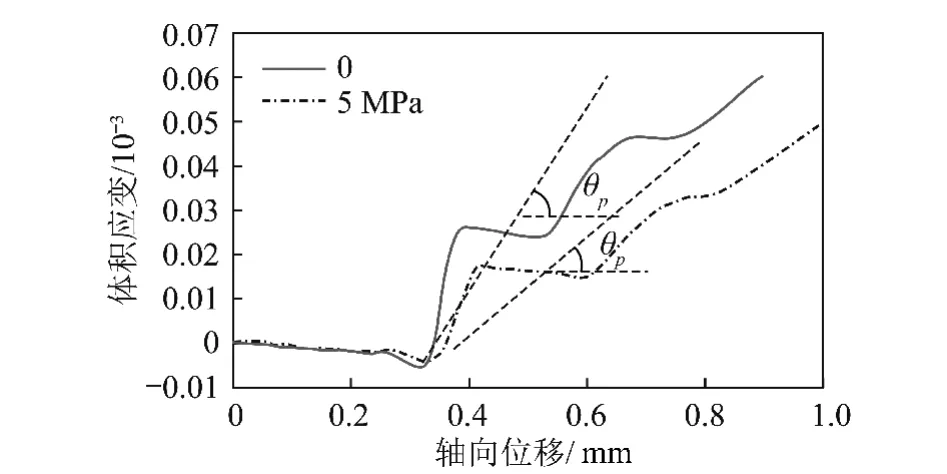
图5 不同围压下试样体积应变-轴向位移曲线Fig.5 Volumetric strain and axial displacement curves under varied confining stress

图6是不同加载阶段岩样的破裂及渗透率情况。图6中(a)～(f)分别对应图4中的不同加载阶段。

在图4中,点A,B,C,D,E为单轴加载条件下不同的加载阶段,点F为围压为5 MPa下加载的应力-轴向位移峰值点。

从图6(a)可以看出,当轴向位移较小时,岩样内部单元没有发生破坏,岩样体积压缩,孔隙率减小,渗透率降低。由于岩样的非均质,各单元压缩程度不同,因此渗透率分布不均匀。

当轴向位移继续增长,但还远未达到岩石的峰值强度时,岩样内的部分单元发生了破坏,这些破坏单元一般先从岩样角部开展,随着轴向位移的继续增加,一些缺陷开始沿轴向长大,当缺陷长大到一定程度时,相邻的平行缺陷(雁列)可能存在显著的相互影响和作用,致使部分长大的缺陷在倾斜的方向上聚结,初步形成了倾斜、断续、狭窄的剪切破裂带。与上述过程相伴随的是,岩样破坏单元的渗透率显著增长。在岩样尚未达到其峰值强度前,部分单元的渗透率已增长了103～105倍,一些未破坏单元的渗透率由于孔隙压缩而呈下降趋势,这与试验获得的规律基本一致[14],如图6(b)～(d)所示。

当倾斜的剪切带初步形成之后,岩样沿剪切带方向的错动越来越明显,致使剪切带方向上的其他未发生破坏的单元都发生了剪切破坏,剪切带看起来更连续、平直、宽阔,岩样也达到了其峰值强度,大量破坏单元的渗透率也都有较大幅度的增长,如图6(d)所示。达到峰值强度后,大量单元破坏,强度和模量退化,进而引起更多单元发生破坏,岩样基本整体发生破坏,绝大多数单元的渗透率都有所增长,渗透率沿剪切带方向呈共轭分布,如图6(e)所示。

图6(f)是围压5 MPa条件下,岩样在峰值强度点的破坏和渗透率情况。对比图6(f)和(d)的破坏形态可以发现,有围压条件下岩样的破坏形态与无围压的破坏形态基本相同,但前者的破坏单元数少。分析岩样的宏观渗透率,当轴向应力达到岩样的峰值强度时,岩样的宏观渗透率增长,单轴情况下渗透率增长了1.21倍,5 MPa围压下渗透率增长了1.03倍,这主要是岩样内部出现了贯通的宏观裂纹,在裂隙带范围内单元渗透率增大所致。

对比图6(f)和(d)的渗透率情况可以发现,围压对岩样的渗透率发展有很大影响。围压的存在大大限制了岩样的剪胀,从而使得单元破坏后的渗透率增长变得缓慢得多。这与试验和理论研究的结论一致。

图6 不同加载阶段渗透率和岩样破坏变化情况Fig.6 Permeability and failure change of rock sample under varied loading stage

另外,从式(31)和(33)可以看出,单元的渗透率与单元尺寸有一定关系,即网格划分可能对岩样局部的渗透率有影响。单元尺寸越小,可能越有利于模拟岩样内部的渗透率变化,但岩样的宏观渗透率是大量单元渗透率的集体效应,试算表明,当网格尺寸小到一定程度时,再细化网格对单元的宏观渗透率影响不大。另外,本文划分的网格已足够小,再细化网格对岩样宏观渗透率已无大的影响。限于篇幅,关于网格尺寸对计算渗透率的影响本文不作详细讨论,这方面的讨论将另文介绍。

7 结 论

(1)在加载初期,岩样发生弹性压缩,体积应变为压缩,岩样的体积减小,渗透率降低。当应力达到峰值强度时,岩样发生剪切破裂,剪切面上颗粒之间发生相对滑动,岩样的孔隙或裂隙空间增加,出现剪胀扩容现象。

(2)该模型可以描述岩石在不同加载阶段及不同围压下,岩样的破裂及渗透率变化情况。同时围压的存在大大限制了岩样的剪胀,从而使得单元破坏后的渗透率增长变得缓慢。

(3)单元的渗透率与单元尺寸有一定关系,即网格划分可能对岩样局部的渗透率有影响。单元尺寸越小,可能越有利于模拟岩样内部的渗透率变化。

参考文献:

[1] 张春会.非均匀、随机裂隙展布岩体渗流应力耦合模型[J].煤炭学报,2009,34(11):1460-1464.

Zhang Chunhui.Seepage-stress coupled model of heterogeneous and random fractured rock mass[J].Journal of China Coal Society, 2009,34(11):1460-1464.

[2] 朱万成,杨天鸿,霍中刚,等.基于数字图像处理技术的煤层瓦斯渗流过程数值模拟[J].煤炭学报,2009,34(1):18-23.

Zhu Wancheng,Yang Tianhong,Huo Zhonggang,et al.Numerical simulation on gas flow through coal seam based on digital imagebased technique[J].Journal of China Coal Society,2009,34(1):18 -23.

[3] 张春会,于永江,岳宏亮,等.考虑Klinbenberg效应的煤中应力-渗流耦合数学模型[J].岩土力学,2010,31(10):3217-3222.

Zhang Chunhui,Yu Yongjiang,Yue Hongliang,et al.Seepage-stress coupled model of coal with Klinbenberg effect[J].Rock and Soil Mechanics,2010,31(10):3217-3222.

[4] 龚 敏,文 斌,王德胜.穿层爆破在南桐矿瓦斯抽放中的应用与数值模拟[J].岩土力学,2012,33(6):1822-1828.

Gong Min,Wen Bin,Wang Desheng.Numerical simulation of blasting through strata for gas drainage in Nantong Coal Mine and its application[J].Rock and Soil Mechanics,2012,33(6):1822-1828.

[5] 周红星,王 亮,程远平,等.低透气性强突出煤层瓦斯抽采导流通道的构建及应用[J].煤炭学报,2012,37(9):1456-1460.

Zhou Hongxing,Wang Liang,Cheng Yuanping,et al.Guide channel construction for gas drainage and its applications in coal seams with low permeability and strong burst-pronenees[J].Journal of China Coal Society,2012,37(9):1456-1460.

[6] 白 冰.核废料储库周边介质热力耦合数值分析[J].岩土力学,2004,25(12):1989-1993.

Bai Bing.Thermo mechanical coupling analysis of nuclear waste repository[J].Rock and Soil Mechanics,2004,25(12):1989-1993.

[7] 张玉军.核废料处置概念库近场热-水-应力耦合模型及数值分析[J].岩土力学,2007,28(1):17-23.

Zhang Yujun.Coupled thermo-hydro-mechanical model and relevant numerical analysis fornear field of conceptual nuclear waste repository[J].Rock and Soil Mechanics,2007,28(1):17-23.

[8] Pan Zhejun,Luke D.Impact of coal seam as interlayer on CO2storage in saline aquifers:A reservoir simulation study[J].International Journal of Greenhouse Gas Control,2011,1:99-114.

[9] 朱珍德,张爱军,徐卫亚.脆性岩石全应力-应变过程渗流特性试验研究[J].岩土力学,2002,23(5):555-559.

Zhu Zhende,Zhang Aijun,Xu Weiya.Experimental research on complete stress-strain process seepage charactenstics of brittle rock[J].Rock and Soil Mechanics,2002,23(5):555-559.

[10] 祝 捷,姜耀东,孟 磊,等.载荷作用下煤体变形与渗透性的相关性研究[J].煤炭学报,2012,37(6):984-988.

Zhu Jie,Jiang Yaodong,Meng Lei,et al.Pertinence study on deformation and permeability of coal containing methane during loading process[J].Journal of China Coal Society,2012,37(6):984-988.

[11] 张东明,胡千庭,袁地镜.成型煤样瓦斯渗流的实验研究[J].煤炭学报,2011,36(2):288-292.

Zhang Dongming,Hu Qianting,Yuan Dijing.An experiment research on gas seepage of stamdard coal briquette specimen[J].Journal of China Coal Society,2011,36(2):288-292.

[12] 蒋长宝,黄 滚,黄启翔.含瓦斯煤多级式卸围压变形破坏及渗透率演化规律实验[J].煤炭学报,2011,36(12):2039-2043.

Jiang Changbao,Huang Gun,Huang Qixiang.Experiment on deformation failure and permeability evolution law of gas-containing coal under multi-stage unloading confining pressure[J].Journal of China Coal Society,2011,36(12):2039-2043.

[13] 王广荣,薛东杰,郜海莲,等.煤岩全应力应变过程中渗透特性的研究[J].煤炭学报,2012,37(1):107-112.

Wang Guangrong,Xue Dongjie,Gao Hailian,et al.Study on permeability characteristics of coal rock in complete stress-strain process [J].Journal of China Coal Society,2012,37(1):107-112.

[14] Fang Z,Harrison J P.A mechanical degradation index for rock[J].International Journal of Rock Mechanics&Mining Sciences,2011, 38:1193-1199.

Permeability evolution model for loaded rock and numerical analysis

YU Yong-jiang1,ZHANG Chun-hui2,ZHAO Quan-sheng2,WANG Lai-gui1
(1.College of Mining Engineering,Liaoning Technical University,Fuxin 123000,China;2.School of Civil Engineering,Hebei University of Science and Technology,Shijiazhuang 050018,China)

To reflect the permeability change of loaded rock,the relationship between the permeability and stress-strain curve of rock was analyzed,and the process the deformation and failure of rock was supposed to be elastic,brittle and plastic.Based on the process the permeability evolution model for rock was presented.In this model the evolution of the permeability for the rock element include:①The permeability can be expressed by porosity during elastic deformation phase.② In the post-peak stage a shear failure rock element may be represented hydraulically as a unit of rock containing two oblique crossing conjugate fractures.③In the post-peak stage a tension failure rock element may be represented hydraulically as a unit of rock containing two orthogonal fractures.Then based on so-called cubic law between smooth parallel plates the permeability evolution model during dilation was presented.In the model the dilation effects of failed element on permeability was considered.Fish function method was adopted to implement the model in FLAC software.The permeability evolution process of a cubic loading rock sample under varied confined stress was simulated.The results show that the model can better reflect the permeability evolution due to elastic deformation or failure.Besides the effect of confined stress on permeability can also be better expressed.

TD313

A

0253-9993(2014)05-0841-08?

于永江,张春会,赵全胜,等.承载围岩渗透率演化模型及数值分析[J].煤炭学报,2014,39(5):841-848.

10.13225/j.cnki.jccs.2014.0028

Yu Yongjiang,Zhang Chunhui,Zhao Quansheng,et al.Permeability evolution model for loaded rock and numerical analysis[J].Journal of China Coal Society,2014,39(5):841-848.doi:10.13225/j.cnki.jccs.2014.0028

2014-01-06 责任编辑:常 琛

国家自然科学基金面上资助项目(51174106,51274079);河北省自然科学基金资助项目(E2013208148)

于永江(1971—),男,内蒙古商都人,讲师,博士后。E-mail:yuyongjiang001@163.com。通讯作者:张春会(1976—),男,教授,博士后。E-mail:zhangchunhui789@126.com