数学：连接有限与无限的金桥——读赵焕光教授等《梦想相遇无穷》有感

季理真，章勤琼（译）

（1．密歇根大学，美国 密歇根 48109；2．温州大学，浙江 温州 325035；3．南京师范大学，江苏 南京 210023）

数学：连接有限与无限的金桥
——读赵焕光教授等《梦想相遇无穷》有感

季理真1，章勤琼（译）2，3

（1．密歇根大学，美国 密歇根 48109；2．温州大学，浙江 温州 325035；3．南京师范大学，江苏 南京 210023）

在数学中，无穷的概念非常重要，处于中心地位．从著作《梦想相遇无穷》出发，讨论无穷以及与之相关的几个概念，如完备、紧致、退化等，进而探讨当代数学中由这些概念导出的主要理论与定理．

无穷；极限；完备；紧致；退化

与初等数学以常量为研究对象，以静止观点研究问题不同，高等数学的研究对象主要为变量，让运动和辩证法进入了数学．微积分是高等数学的基础课程，也是学习许多其它课程的重要工具．微积分以函数为研究对象，通过连续这一桥梁，利用极限为主要方法进行研究．由于微积分有关概念的相对抽象性，不少学生在初学时感到枯燥与困难．因此，为了有助于学生更容易理解微积分相关概念，产生进一步学习与探索的兴趣与欲望，有必要从数学、哲学、历史、人文等更宽广的视野出发，对微积分中的一些重要概念做出阐释．

1 无 穷

自人类文明开始以来，人们就已经开始思考并探索无穷的意义．在有限的生命内，由于空间与能力的限制，人们经常会遇到不易解决的难题，出于各种原因，他们只能将问题转向无穷的上帝或众神．

哲学家们通常也会深入思考这一问题，试着去理解并解释无穷．但究竟什么是无穷？数千年以前，古希腊哲学家已经提出更精确的问题，他们知道如何对有限数字进行加与除．但如何理解无穷过程并处理无限数字呢？

关于无穷的严格系统理论是晚近才由奇特的数学家康托尔创造出来的．与有限对象相比，人们过去会认为存在一个单独的无穷集合或无穷量，独立于所有其余的集合或量，本身并没有什么结构．但康托尔说存在不同形式的无穷集合，而无穷集合的世界非常复杂，甚至比有限集的世界还要丰富，而且直接对其产生影响．

康托尔的理论，或者说他的观点，已经永远改变了数学的全部景观，从数学的基础直至当代数学的最前沿．因此，为了理解并欣赏数学的精妙与美，有必要接触并熟悉无穷．

温州大学赵焕光教授、应裕林副教授等合著的《梦想相遇无穷》，从数学、历史以及哲学的观点对无穷理论作了初步介绍．这是一本真正讨论数学的文化著作，全书不失趣味性与可读性，而且适合高中生与大学生阅读．我多么希望数十年前我在大学一年级开始学习微积分时，能有机会阅读这样的书．

2 极限与连续

如何将无穷的观点与数量应用到有限的函数与空间中？我们知道有无穷小与无穷大的数量与空间，而它们之间的相互作用就像一支永不停歇的探戈，刺激着数学长河川流不息的发展．其中最好的例子可能是微分与积分的对偶理论，以及将两者联系起来的微积分基本定理．

在这两个理论中，极限与连续的概念都非常关键．如何接近才是足够接近？多大才是足够大？前者需要期望有多小就有多小，而后者则是需要期望有多大就有多大．这两种情形都是无限的过程．

在定义这些概念之前，函数存在的空间必须能支持这些无限运算．在有理数集内，对达成上述目的并不完备，需要在有理数之间通过一个无限的过程将无理数添加进去构成一个没有空洞或缺口的实数连续统集．这本著作正是从基本的集合论与实数构造的戴德金分割开始的．

3 完 备 性

从有理数集到实数集的完备可能是最早的完备化．除此之外，还有许多种，甚至可以说有无穷多种相关的完备化和紧致化方式．每个学生都知道无限级数

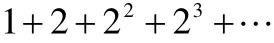
的部分和形成一个发散于实数轴上的无穷有理数列，即

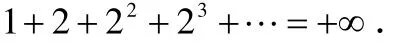
但若我们应用著名的公式

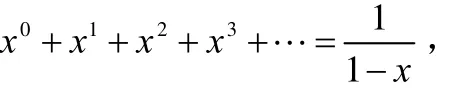
并且无视条件1||＜x，那答案将是

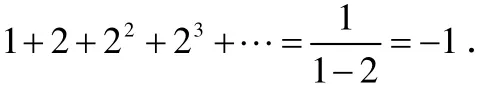
这样，就从无限的运算中得到了有限数-1．但是正数的和怎么能是负数呢？这似乎是不可能的．然而，如果用不同的方式对有理数域进行完备化，这样是可以正确而且可取的．可以声明，当n 充分大时，2n是充分小的．这样一个度量在2进制数域Q2中是成立的，Q2是p进制数域Qp的一个特殊情况，其中p是一个素数．

现代数学或数论的一个基本观点是从Q到R的嵌入的方式，仅仅是无穷多种完备化中的一种．在这些完备化中，每一种都对应一个素数p或无穷∞．

我们需要用无穷的观点来处理有限的有理数．上面的示例还显示出无穷大和无穷小之间的关系可以比人们预想的更有趣．

分析的核心由微分与积分组成．我们都知道，牛顿和莱布尼兹共同发明了微积分．他们之间工作的区别是什么？在他们之前，还有谁作出了重要贡献？在他们的工作之后又发生了什么？这本著作提供了细致且生动的论述来回答这些问题．有哪个学习微积分的学生会不想知道这其中完整的故事呢？

连续函数积分的引入可以看作是另一种形式的完备化的开始，它是一个建立在先前的无限过程之上的无限过程．比如说，给定一个有限区间[0, 1]，我们用积分定义一个在[0, 1]上的连续函数的距离，它像有理数域的情况一样不完备．为了更好地理解这个空间，我们需要通过添加一些理想的函数来使之完备化．这个无穷过程将引导我们离开本书的话题（或者说离开我们所考虑的函数）并进入一个更广阔的泛函分析世界，而这正是本书第一作者赵教授的专长之一．

就像将Q 完备化为R和Qp的情形一样，若往其中添加可测函数，关于这类函数空间（巴拿赫空间和希尔伯特空间）也有无限多种完备化方法．这些概念对于目前还不了解它们的读者而言并不十分重要，然而重要的一点是，需要以无限的过程去理解有限的事情．

4 紧致与退化

在有限与无限的对象之间还有另一个有关联的交互．实直线R是无限的，如果有人沿着实直线的任一方向行走，他永远都到达不了某一个点．但如果在无限中添加一个点，将R无穷的两个方向包起来，就得到了一个圆．这里的关键之处是在无限中添加了一个理想的点．戴德金分割的核心之处就是在有理数之间添加理想点．

紧致化的理论以及走向无限的想法在当代数学中被广泛地运用．有关数学对象退化的探讨同样与之相关，比如流形．佩雷尔曼（G. Perelman，1966—，俄罗斯数学家，2006年第25届数学家大会欲为他颁发菲尔兹奖，但他拒绝领取）在三维拓扑学中著名的庞加莱猜想和莫斯托（G. D. Mostow，1923—， 美国数学家，获2013年沃尔夫奖）强刚性重要结论的证明中都运用了这种方法．

该书常将哲学层面的讨论融入到数学结论中．这种在更广阔的视野从无穷的角度来看待事物的观点，在生活中也非常有用．它能够帮助人们过滤掉无关紧要的事物而突显出什么才是人生中真正重要的，这一方法也常常被人们用到数学证明中．

5 小 结

这一著作是源于对数学的爱的劳动成果．作者试图向读者传递他们对数学的热情以及数学与人文，诸如中国古代文献以及中西方哲学的关联．本书对与无穷、极限以及微积分相关的数学结论与例子给出了全面的描述．她同样涵盖了连续与离散数学的世界．本书可以作为微积分标准教材之外良好的补充读物，因为书中诸多的评论与历史事实可以拓宽读者的视野．而从上面的论述可以看出，本书还能作为了解数学中更高深主题的桥梁．

本书的另一特点是其中引用了近几个世纪以来著名数学家的许多名言．通过阅读本书，读者可以与人类历史上的伟大心灵一起，探索数学核心概念以及它们的分支．

本书仅是赵焕光教授与他的合作者们的系列著作中的一本，这一系列著作试图以一种友好与轻松的方式展现数学的综合面貌．如果人们愿意挑选这一系列著作阅读或浏览，将会有助于他们对数学有更好的理解．作者们承担如此宏大工程所付出的努力及其勇气，必将受到数学爱好者、学习数学的学生和数学研究工作者的钦佩与赞赏．

注：《梦想相遇无穷》为科学出版社《文化数学欣赏丛书》的第3本．该系列丛书共6本，分别为《生活相遇数学》、《人生相遇函数》、《梦想相遇无穷》、《真理相遇统计》、《文明相遇几何》以及《智慧相遇代数》．目前，《生活相遇数学》、《人生相遇函数》与《梦想相遇无穷》已出版．

致谢：本文的主体内容为季理真教授为《梦想相遇无穷》所作的序言，由章勤琼译成中文，文中的第一段及最后的注为译者在与作者讨论后所加．温州大学王玮明教授等对译文提出了宝贵意见，在此一并感谢．

Golden Bridge between Infinite and Finite: Mathematics

JI Li-zhen1, ZHANG Qin-qiong2,3
(1. University of Michigan, Michigan USA, 48109; 2. Wenzhou University, Zhejiang Wenzhou 325035, China; 3. Nanjing Normal University, Jiangsu Nanjing 210023, China)

The notion of infinity is of central importance in mathematics. In this article, we start from the book “When Dreams Encounter Infinity” and discuss how several related concepts such as completion, compactification, degeneration lead to major theories and theorems in contemporary mathematics.

infinite; limit; completion; compactification; degeneration

G40-03

：A

：1004–9894（2014）02–0093–02

[责任编校：周学智]

2014–01–07

季理真（1964—），男，浙江温州人，美国密歇根大学教授，浙江大学光彪特聘教授，主要从事几何、拓扑、数论及数学交叉学科等研究．章勤琼为本文通讯作者．