中法高中数学课标微积分内容比较研究

张玉环，Alаin Lеgеr

（1．河南大学 数学与信息科学学院，河南 开封 475004；2．首都师范大学 数学科学学院，北京 100048；3．法国国家科学研究院 力学与声学研究所，法国 马赛 13402）

中法高中数学课标微积分内容比较研究

张玉环1，2，Alаin Lеgеr3

（1．河南大学 数学与信息科学学院，河南 开封 475004；2．首都师范大学 数学科学学院，北京 100048；3．法国国家科学研究院 力学与声学研究所，法国 马赛 13402）

为追求更高的教学质量，中法两国一直不断地调整高中微积分的教学内容．比较法国2010和2011年公布的高中最新数学大纲中的微积分与中国2003年颁布的《高中数学课程标准》中的微积分内容，建议中国高中微积分教学应缩小知识跨度，加强分层教育，注重微积分与实际以及其它学科的联系，且进一步加强微积分教学与信息技术的整合．

数学课标；微积分；高中；中法比较

1 引 言

在历史上，法国是注重理性思维传统的国家，曾产生过像笛卡尔、费马等著名的大数学家，特别是18世纪末、19世纪初，巴黎几乎成为当时世界数学发展的晴雨表[1]．当前法国在科学研究领域仍扮演着重要角色，特别是数学．2006年在马德里召开的国际数学家大会上，有25%的发言人是法国数学家．在其它科学领域法国也是名列前茅[2]，并且法国精英教育与大众教育能合理并存[3]．由此可知，法国的中小学教育取得了不错的成绩．

如何在高中开设微积分？它的定位如何？一直是国内外教育界研究的焦点问题．2003年国内开始实施新课标[4]，以逾越极限的形式来讲微积分．时至今日高中微积分仍然面临着不少问题．孙晓天教授说：开阔视野，环顾左右，看看别人是怎么做的，想想自己是怎么做的，再思考自己下一步该怎么做，才能把事情做的更好[5]．这里主要探讨法国高中最新数学大纲微积分内容的设置、编排和目标要求，并与中国现行课标中的微积分内容进行对比，以期对中国高中微积分课程改革与教学有所启示．

2 法国高中教育体制

法国小学5年，初中4年，高中分为普通高中、技术高中和职业高中，前两者学制是3年，职业高中是2～4年．普通和技术会考成绩合格者，可直接进入普通综合大学学习，但要进入大学校（即精英学校），还需先考入该类学校的预科班学习两年后再考试，成绩优秀者才被录取．大约一半的学生在职业学校，一半的学生在普通高中和技术高中（后者可能更多一些），大多数的数学系学生或数学家来自普通高中．这里主要介绍普通高中的情况．从高二开始分专业，主要有L（文学、语言、哲学和艺术）、ES（经济和社会科学）、S（自然科学）．各年级3个专业数学课程时间安排：高一（Sесоndе）每周4～5个小时；L、ES、S三个专业，高二（Prеmièrе）学生分别为2～5小时、3～5小时、5小时，高三（Tеrminаl）学生分别为0～3小时、4～6小时、5.5～7.5小时．各个年级和方向都有全国教学大纲，它们是由数学教师、数学工作者和数学专家一起编制的．在实施以前，先在某些学校进行实验．教科书根据教学大纲自由编制，但学校有选择权[6，7]．

3 中法两国高中微积分内容的历史变革

1938年法国就在高中数学内容中增加了微积分，后来为追求更高的教学质量，法国一直不断调整分科制度和课程设置．1969年理科大纲的高中微积分试图建立在逼近思想的分析基础上，需要介绍实数集合的完备性公理和极限的定义；鼓励基本定理的证明，如中值定理，但不需要形式的证明；在高二（自然科学方向）介绍欧拉方法，但因过分强调数学的抽象性、普遍性，忽视数学的实际应用，1981年宣告失败，后来又几经修改，大约每10年变动一次．前几年的微积分内容，涵盖数列极限、函数极限、区间连续、导数、极值、定积分及基本定理等，基本上是大学微积分的缩影．2008年萨克奇公布了中学教育改革计划，要调整教学课时，课程内容以及评价方式．法国高中于2010年开始实施新的教学大纲[6～10]．

1866年中国在高中（当时称为高等学堂）开设了“微积分”课程，一直到1923年．随后在相当长的时间内取消了微积分课程，仅在代数中讲一点极限论初步知识．1960年至1963年编写了“微积分”试用教材．然而，1962年至1965年只讲数列和极限．1977年开始重新编写全国通用的中学数学教材，增加微积分．遗憾的是，受高考指挥棒的影响，微积分教学实际上被取消[11]．2000年3月正式出版的大纲，再次将微积分初步的知识作为选修的课程内容，在理科选修中，微积分部分包括极限、导数和微分、积分；文科则只学习极限和导数部分[12]．现行课程标准微积分内容改革力度比较大，以逾越形式化极限概念来讲微积分[13]，且仍将其列为选修课，高考会略有涉及．文科16学时，只讲导数及应用．理科为24课时，讲导数及其应用、定积分及微积分基本定理．

4 法国大纲中微积分内容介绍

法国普通高中，一年级只有一个数学大纲，从高二开始文学专业和经济社会专业共用的一个数学大纲（简称文科大纲），以及理科专业大纲．学生从高二开始学微积分，一直到高三．这里主要探讨涉及微积分内容的最新教学大纲，即2010年公布的高二理科大纲[14]和高二文科大纲[15]，2011年公布的高三理科大纲[16]和高三文科大纲[17]．表1和表2分别把高二、高三文科大纲中微积分部分内容列了出来．其中第一栏是基本内容，包括基本概念、性质以及定理等；第二栏是要求学生要达到的最低能力，明确指出了教学目标；第三栏是加以注释或补充说明，给教师提供教学建议，学生完成学习任务需要用到的器具，学生之间交流的内容，对数学证明的要求以及其它比较困难的内容．表中还专门标注了一些算法活动．

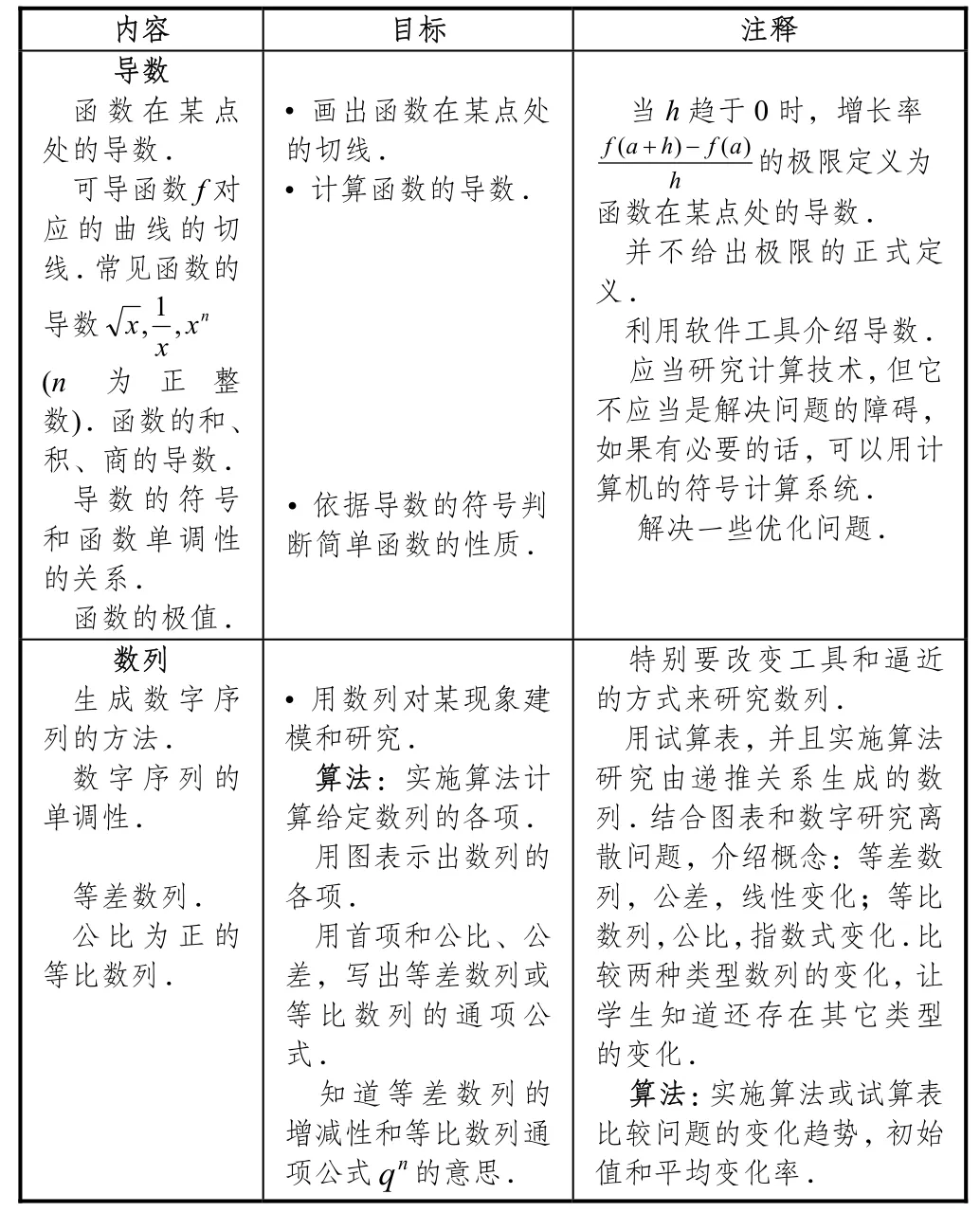
表1 高二文科大纲（微积分部分）

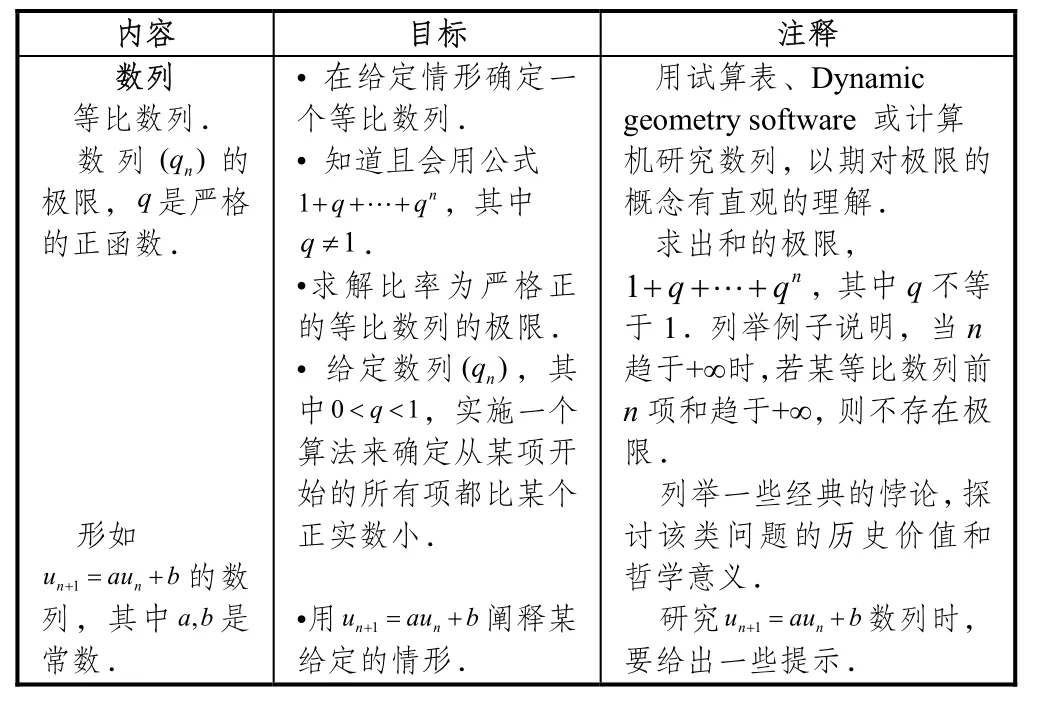
表2 高三文科大纲（微积分部分）

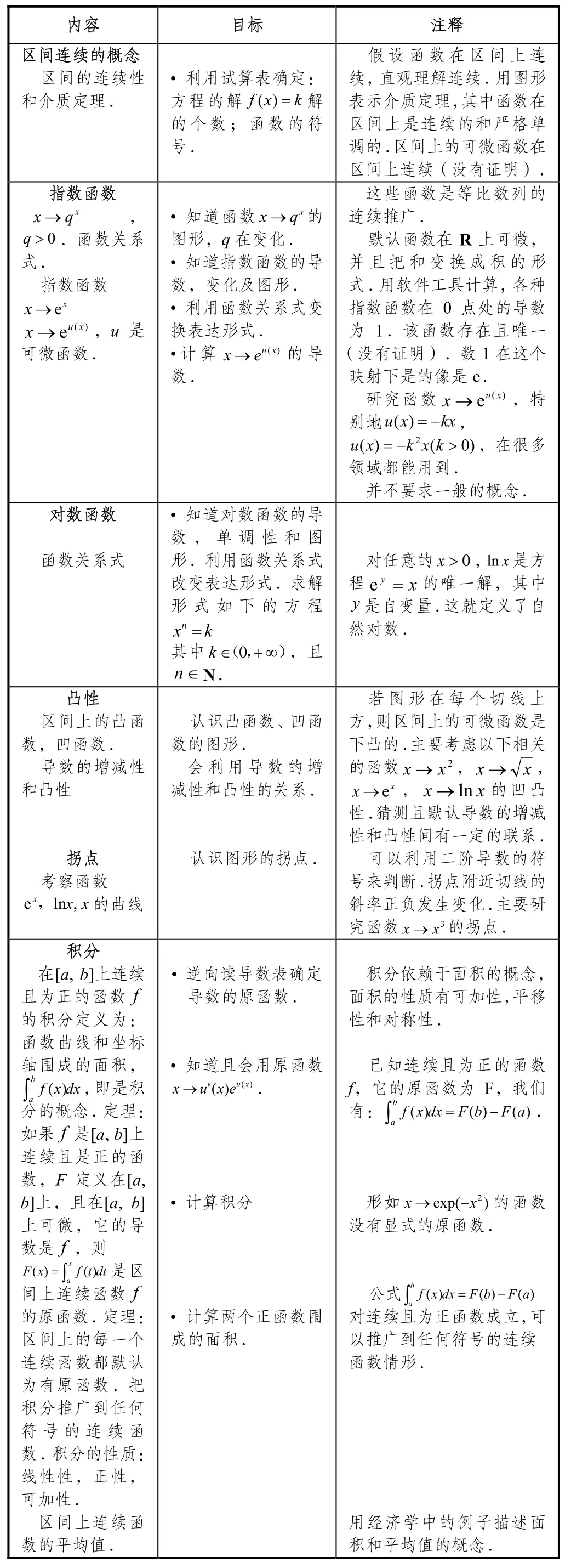
表2 （续） 高三文科大纲（微积分部分）

下面简要介绍文科大纲中微积分内容的设置理念．高二，其动机仍和高一相同，要解决纯数学或其它相关学科的问题．介绍一个新的工具——导数．这一阶段研究的函数都是正则的，能够直观地理解某点处有限极限的概念．研究很多领域的变化现象，包括经济、社会科学，用数列对它们进行模拟．基于不同领域的离散现象介绍数列的概念，并且实施算法或试算表，这样有助于对概念的理解．高三，继续研究等比数列来学习极限的概念．介绍指数函数和自然对数函数及其导数，指数函数是把离散问题转变到连续问题的一个契机．介绍函数的凸凹性、拐点概念，主要用来研究图形，并且在经济学中有着广泛的应用，特别是成本方面的问题．最后学习积分的概念，有保留地讨论和研究，只涉及分析里的基本概念．

以微积分内容方面来说，新大纲改革力度不太大．以理科大纲为例，和前几年理科大纲相比[9]，去掉了一些知识点，如可导函数相应的线性逼近，证明极限的唯一性，不证明地使用数列的商、乘积定理，微分方程等；高三增加了正弦、余弦函数及其导数；把一些知识从高二移到了高三，如数列的夹逼定理、渐近线等．

5 中法课标微积分内容的相同点

5.1 立足于学生

法国大纲中，学习微积分不仅要培养益于学生一生的学习技巧和能力，更好地了解社会，而且要训练学生坚实的数学底子，为日后学习、科研做准备．

中国课标中，让学生体会导数的思想及其丰富内涵，感受导数在解决实际问题中的作用，了解微积分的文化价值，而且为大学的进一步学习打基础．

5.2 有部分相同的知识点

就法国理科大纲和中国理科课标来说，两者都包括的知识点有：导数概念和几何意义，能进行简单函数的导数运算，如y=，y=，y=xn（n≤3且为正整数），导数在研究函数中的应用，如函数单调性与导数符号的关系，函数极值问题，生活中的一些优化问题，定积分与基本定理等．

5.3 很少的证明

法国理科大纲里，要求的证明比较少，如数列（qn）（其中q＞1）的极限是无穷大；如果某一数列递增，且极限为l，那么从某一项开始的所有项都小于或等于l；证明R上满足f′=f，f (0)=1的可微函数是唯一的，存在性不需要证明．数列夹逼定理，单调有界收敛定理，介质定理，区间上的可微函数连续，积分定理等则明确标注不要求证明．定理：区间上连续且为正的函数存在原函数，只要求部分证明，即证明区间为有界闭集的情况．文科大纲的证明更少．

中国课标中几乎没有要求任何有关微积分的证明．

5.4 重视数学文化

法国大纲要求，在大纲实施的过程中揉合数学思想和历史，知道一些著名数学家的名字，他们生活的年代以及他们的贡献是整个数学文化和技术的一部分，了解概念的形成和演变的历史，有助于学生对概念的理解．该部分知识内容较多，很大一部分内容需要学生在课外学习，要考虑到每个学生的特点来设计该部分，特别要和目标相一致．考核形式也要多样化．

中国课标要求，数学文化尽可能有机结合高中课程内容，选择介绍对数学发展起重大作用的历史事件和人物，让学生认识数学发生、发展的必然规律，了解数学真理的相对性，提高学生兴趣．并且对微积分这部分内容提出了具体的建议，介绍微积分创立的时代背景及人物资料，如牛顿、莱布尼茨，以及微积分在文艺复兴后对科学、社会、人类思想进步的推动作用．这部分知识建议采取多样化的教学．

5.5 重视理论与实际相结合

法国大纲一直强调让知识运转起来，且在解决实际问题中学习知识，然后再加以应用．微积分内容的其中一个目标是学生最终能够利用数学工具，如函数、数列、导数以及积分等，处理连续、离散的现实问题．国家教学委员在关于“数学大纲的框架信中”指出，应该为学生提供各种各样的背景（地理、经济、生物、时事等）中的事例，以使学生获得的能力不局限于单纯的“数学课”[18]．

中国课标注重数学知识和实际的联系，发展学生的应用意识和能力．通过丰富的实例引入数学知识，引导学生应用数学知识解决实际问题，经历探索、解决问题的过程，描述数学的应用价值．帮助学生认识到：数学与我有关，与实际生活有关，数学是有用的，我要用数学，我能用数学．

6 中法课标微积分内容的异同点

6.1 教学目标

法国两个大纲的动机都是解决纯数学或其它学科的问题，特别是利用这些数学工具（数列、函数、导数以及积分）解决现实生活中离散、连续问题．理科的学生要求掌握一些简单的证明，一些算法活动，设置了一些开放性的交叉学科题目，而且专门为有特殊需要的学生设置了难度较大的内容．文科要求较少的一些算法活动，特别要学习函数的凸凹性及拐点等概念，便于研究图形，且在经济学中有着广泛的应用．

中国课标要求，理解导数的含义，体会导数的思想和内涵；应用导数在探索函数单调性、极值等性质及在实际中的应用．对理科生多了一个要求，即初步了解定积分的概念．

6.2 知识点的深度和广度

法国大纲中的微积分是必修内容．知识点范围广，包括数列极限、函数极限、函数连续、导数、积分，要求的程度较高；内容选择和设计基本按大学微积分的套路进行，只是没有了详细的推导，证明也比较少．

中国课标把微积分放在选修中，以逾越极限的形式来讲微积分，完全从直观理解出发，整体要求比较浅．

6.3 编排方式

法国大纲中把微积分放在高二、高三两个年级学习，且从高二到高三，知识点逐步加深．某些难度较大的知识点或概念不会一下子呈现给学生，如数列极限、函数极限等概念，让学生见过几次后，才逐步固定下来．

中国课标把微积分基本内容放在了一个模块中．

6.4 层次教育

法国大纲中微积分内容，突出了不同层次学生的要求，对有特殊需要的学生标注了一些较难的知识点供．比如，理科大纲中，讲数列时对р，е黄金分割率进行逼近计算，研究演化现象，列出不连续函数或不连续导数的例子，计算物体的体积，等等．

而中国课标中的微积分内容则没有如此的设计．

6.5 学科之间的交叉与渗透

法国大纲中会有一些交叉性学科的开放性课题，可以让学生自主讨论或咨询其它学科的老师，如理科大纲讲正弦函数、余弦函数时涉及传播的波，讲指数函数时有放射性的题目，讲对数函数时涉及变换器、声音的强度、地震的震别及PH值的范围等内容，讲平均值时有匀加速运动，能量转移知识，等等．

中国课标中，虽然也有优化问题，变力做功等综合方面的实际问题，基本上都以相对简单的例子或习题出现，并不是开放性的探索性题目，学生也一般不会或不习惯于去咨询其它学科的老师．

6.6 算法实施和软件的使用

法国大纲中要求算法和推理并重，且贯穿在整个大纲的始终．强调让学生掌握一定的算法，会用试算表、Dynаmiс Gеоmеtry Sоftwаrе、计算机、计算器或符号计算系统．如理科大纲中要求，用试算表、Dynаmiс Gеоmеtry Sоftwаrе或计算器研究极限，对极限有直观的理解；观察数列的增减速度；编写算法求解方程f(x)=k．文科大纲中的算法要求见表1．两个大纲有好几处都强调：求解问题的过程中，如果问题比较复杂，没必要把时间浪费在计算技巧上，可以借助软件或计算器来计算，让学生专注于逻辑推理、概念理解、知识应用等其它方面．大纲中列出了3种使用软件工具的方式：教师在课堂上集中演示器具；学生在数学的实践中使用；学生课外作业的一部分．

中国课标也注重信息技术与数学课程的整合，提倡利用信息技术来呈现以往教学中难以使用的内容，在保证笔算训练的前提下，尽可能使用科学型计算器、各种数学教育技术平台，加强数学教学与信息技术的整合，鼓励学生运用计算机、计算器等进行探索和发现．

总之，法国大纲对算法实施和软件使用有比较具体的说明，且真正做到了实处；而中国课标在这方面还不够具体，在算法实施和软件使用方面仍不容乐观．

6.7 文理科的差别

法国普通高中3个专业的数学教育各有侧重：文学专业的数学教育注重让学生掌握数字信息和图表信息；经济社会专业的学生需要具备良好的数据信息分析和一定的逻辑推理能力；理科专业注重数学文化功底的同时，更加注重数学的服务功能．于是两个类型数学大纲的微积分内容有明显差别．首先，内容设置方面，文科大纲与理科大纲相比，少了正弦、余弦函数导数，以及渐进线，但增加了百分比和变化之间的联系，函数的凸凹性及拐点，结合学科特点对图形有了更高的要求．其次，教学要求方面，知识点相同的部分，文科比理科要求整体偏低，如文科从等比数列引入指数函数，理科则是通过微分方程引入．并且文科基本上不要求证明，有一些算法活动．而理科大纲中会有一些范例式的证明，其中一些是学习的目标，需要理解和掌握，算法活动比较多，有一些交叉学科的开放性题目，且有一些专门为有特殊需要的学生设置的难度较大的内容．再者，课时安排方面，高三文科专业大纲中要求三分之二的时间学习分析（基本上都是微积分的内容），剩下的时间来讲概率和统计．高三理科大纲要求一半时间学分析，另一半时间学几何和概率统计．并且都强调教师可根据特定的情况做适当的调整．

中国课标中，文科微积分内容总体上来说比理科微积分要求低，比如少了根式函数的求导，不介绍定积分与微积分的基本定理．课时安排方面，文科微积分内容要求16课时，理科要求24课时．

总之，法国数学大纲针对不同学科的特点，在微积分的内容设置、目标要求、课时安排方面都有很大的区分度；而中国文理科之间的差别就没有那么明显．

7 思考及建议

通过中法高中微积分对比，对中国高中微积分课程设置和教学提出一些思考和建议，如微积分教材设置方面，要同时兼顾大众教育和精英教育，缩小高中微积分与大学微积分以及高中微积分知识点之间的知识跨度，注重学科交叉与实际应用；在微积分教学方面，加强现代化信息技术的整合，课堂上尝试自主探究模式，具体如下．

7.1 同时兼顾大众教育和精英教育

中国自义务教育阶段以来，普及化教育和大众化教育被提上日程，似乎把精英教育放到了某个角落．如何能顺应时代潮流，在普及化教育的同时，又能兼顾到精英教育，值得大家深思和关注．根据法国数学教育的特点，有如下两条建议．首先，锐化文理科的差别．文科方面来说，要根据文科生的特点，让微积分概念更加直观、易懂．国内林群[19]、张景中[20]等在微积分初等化方面做出了很多努力．特别是林群的微积分算术，只用几步高中代数就能不失严格地讲微积分．让时间不再浪费在高难度的理论知识上，而是专注于知识的理解和应用，已经有了一些尝试，如文献[21～22]；理科方面，如文献[23]指出：高中阶段如能较为系统地学习微积分知识，可为大学的专业打下良好的基础，再考虑到理科学生逻辑思维能力相对来说比较强，并且以后学习上的需要，可以把理科高中微积分设置得稍微严密些．其次，加强学科内的层次化教学．微积分课程设置要体现时代性、基础性、选择性、多样性的基本理念，兼顾不同层次学生对微积分的求知需求[24]，针对喜欢钻研数学且学习进度比较快的学生，专门设置一些难度较深的知识点和开放性题目．

7.2 缩小知识跨度

无论是中国的高中生还是法国的高中生，在学习微积分时，死记硬背占了很大的比重．在法国马赛大学任教很多年的Elаinе Prаtt教授（私下交流）说：在学习了有很少证明的高中数学教材后，很多大学生甚至不知道什么是证明．她强调：数学课程要特别注意知识点之间的衔接，跨度不能太大．比如，学生学习“点和直线关系”时，碰到“点属于直线或不属于直线”的说法，如果他们不明白什么是“属于”的话，教学应当如何进行下去呢？学生只能生搬硬套，死记硬背了．因此，如何能让学生在高中从常量的、有限的、直观的数学顺利过渡到变化的、无限的、抽象的微积分，并且学过高中微积分后，又如何能无缝衔接到大学微积分？值得每一个课程改革者和教学工作者深思．其中一个基本原则是注重缩小知识跨度，让学生能够吃透，而不是死记硬背来应付考试．

7.3 注重学科交叉与实际应用

微积分教学过程中，一方面要注重学科之间的联系，另一方面要注重理论与实际的联系．法国国家教学大纲委员会在“教学大纲框架信”中指出，现在进入高中的学生越来越多，学科技术小组应该充分考虑到从教育质量和数量两个方面来选定数学教学的内容，要寻找那些可以让学生进行深入数学思考并可以为所有人带来丰富知识的领域，尤其是要通过向当代世界开放而使数学课界限不再那么密不透气，要和其它学科建立联系[18]．中国课标中，注意数学与其它学科及现实世界的联系，特别是导数与现实世界中存在的变化率的联系，通过速度的变化率，体积的膨胀率，以及效率、密度等大量丰富的现实背景引入导数的概念．但在实际教学中，由于高考指挥棒的影响以及时间的限制，这些联系并没有完全走进高中微积分的课堂．因此，需要进一步地关注．

7.4 加强微积分教学与现代化信息技术的整合

随着计算机信息技术的迅猛发展，信息技术与数学教学、数学学习的整合势在必行，且有诸多的益处：对学生来说，一方面，能让学生进行实验、探索的数学发现活动，从多个侧面研究同一个概念或性质，将数字和图形有机地结合在一起，促进学生的理解和掌握．另一方面，计算器或软件可以机械地算比较复杂的问题，让学生专注于逻辑推理等其它方面的学习．对教师来说，合理地使用信息技术能提高他们的教学水平．

国内高中微积分并不讲极限概念．比如，通过实例分析经历由平均变化率过渡到瞬时变化率的过程，学习导数．如果学生能利用软件计算数字，并结合图形直观地感受到，随着时间段的缩小，平均变化率逐渐趋向于一个固定的值，那么对导数的理解就会更上一个台阶．教学与信息整合的原则是利于对数学本质的认识．而国内信息技术和微积分课程内容的整合还有比较大的开发空间．建议政府部门为学校配备齐全的信息技术设备；课程标准要列出具体可行的实施细则；教育部门要加大教师在信息技术方面的培训等．

7.5 课堂上尝试自主探究模式

法国高中比较注重学生个体及小组合作探究活动．由此，想到现阶段国内大多数高中教师反应微积分教学进程比较慢、课时不够用等情况．对此，可以适当调整传统的教学模式，尝试让学生课下分小组自主探究微积分的发现过程以及微积分的实际应用等问题，然后进行交流展示，教师点评．只要教师把握好探究问题的方向、尺度和进程，不仅能提高学生的学习兴趣，而且利于概念的理解和掌握．因为学生必须经过讨论、探索、碰撞的过程，才能把抽象、复杂的微积分内化为自己的知识．

致谢：特别感谢林群院士的指导和帮助．

[1] 张生春，邓明立．十九世纪法国高等教育改革的启示——兼谈法国数学百年兴衰[J]．数学教育学报，2005，14（2）：50-52．

[2] 李亚玲．法国数学家Jеаn-Piеrrе Dеmаilly在华人数学家大会上的报告[J]．数学通报，2008，（2）：21-25．

[3] 杨少琳．双轨制：法国精英教育与大众教育的合理并存[J]．重庆工学院学报（社会科学），2009，23（12）：173-178．

[4] 中华人民共和国教育部．普通高中数学课程标准（实验）[M]．北京：人民教育出版社，2003．

[5] 孙晓天．数学课程发展的国际视野[M]．北京：高等教育出版社，2003．

[6] 米歇尔·阿蒂格．法国高中数学教学[J]．数学通报，2009，（12）：1-4．

[7] 李渺，陈志云．新世纪初的法国数学课程简介[J]．数学通讯，2003，（3）：1-2．

[8] 王媛，苏帆．中法两国中学数学教学内容差异之管窥[J]．中学教研（数学），2004，（5）：1-3．

[9] 法国数学课程标准简介[J]．邓冠铁，高志强译．数学通报，2009，（1）：12-16．

[10] 刘敏．法国高中分科定向及会考制度发展解析[J]．比较教育研究，2009，（10）：56-60．

[11] 匡继昌．如何给中学生讲授微积分[J]．数学通报，2006，（5）：2-4．

[12] 焦彬桥．高中微积分课程内容选择的探索[D]．广西师范大学，2004．

[13] 宋宝和，房元霞．逾越形式化极限概念的微积分课程——《普通高中数学课程标准（实验）》实证研究[J]．数学教育学报，2004，13（4）：55．

[14] Ministèrе dе L′Éduсаtiоn Nаtiоnаlе. Annеxе Mаthémаtiquеs Cyсlе Tеrminаl dе Sériе Sсiеntifiquе Clаss dе Prеmièrе [EB/OL]．httр://mеdiа.еduсаtiоn.gоuv.fr/filе/sресiаl_921/1/mаthsS_155211.рdf, 2010.

[15] Ministèrе dе L′Éduсаtiоn Nаtiоnаlе. Annеxе Mаthémаtiquеs Cyсlе Tеrminаl dе lа Sériе Éсоnоmiquе еt Sосiаlе еt dе lа sériе Litеrаtrе Clаss dе Prеmièrе [EB/OL]. httр://mеdiа.еduсаtiоn.gоuv.fr/filе/sресiаl_9/20/9/mаthsES+L_155209.рdf, 2010.

[16] Ministèrе dе L′Éduсаtiоn Nаtiоnаlе. Annеxе Prоgrаmmе dе L’еnsеignеmеnt Sрéсifiquе еt dе Sрéсiаlité dе Mаthémаtiquеs Clаssе Tеrminаlе dе lа Sériе Sсiеntifiquе [EB/OL]. httр://mеdiа.еduсаtiоn.gоuv.fr/filе/sресiаl__8mеn/ 98/4/mаthеmаtiquеs_S_195984.рdf, 2011.

[17] Ministèrе dе L′Éduсаtiоn Nаtiоnаlе. Annеxе Prоgrаmmе dе L’еnsеignеmеnt Sрéсifiquе еt dе Sрéсiаlité dе Mаthémаtiquеs dе lа Sériе Éсоnоmiquе еt Sосiаlе еt dе L’еnsеignеmеnt dе Sрéсiаlité dе Mаthémаtiquеs dе lа Sériе Littérаirе [EB/OL]. httр://mеdiа.еduсаtiоn. Gоuv.fr/filе/sресiаl_8_mеn/98/2/mаthеmаtiquеs_ES_L_195982.рdf， 2011.

[18] 汪凌．法国普通教育高中的数学教育课程[J]．全球教育展望，2002，31（10）：28-30．

[19] 林群．微积分算术[EB/OL]．科学网博客，2011．

[20] 张景中．微积分学的初等化[J]．华中师范大学学报（自然科学版），2006，（12）：475-484．

[21] Yuhuаn Zhаng. Cаlсulus оf Elеmеntаry Funсtiоns - A Prеfеr Oрtiоn fоr Tеxtbооks оf High Sсhооl [A]. In: Xiаоhui Guо. 2011 Intеrnаtiоnаl Cоnfеrеnсе оn Cоmрutеr Aррliсаtiоn аnd Eduсаtiоn Tесhnоlоgy[C]. HоngKоng: Sсiеnсе Tесhnоlоgy Prеss, 2011．

[22] 李红玲．现有大学文科数学教材中存在不足的思考[J]．数学教育学报，2012，21（1）：92-94．

[23] 马峰．基于实践的高中微积分课程比较研究[J]．数学教育学报，2011，20（6）：59-63．

[24] 胡典顺．新课程中的微积分及其教育价值[J]．数学教育学报，2010，19（1）：13-16．

Comparison on the Standard of Calculus in Mathematics Curriculum of Senior High Schools between China and France

ZHANG Yu-huаn1，2, Alаin Lеgеr3
(1. Sсhооl оf Mаthеmаtiсs аnd Infоrmаtiоn Sсiеnсеs, Hеnаn Univеrsity, Hеnаn Kаifеng 475004, Chinа; 2. Sсhооl оf Mаthеmаtiсаl Sсiеnсеs, Cарitаl Nоrmаl Univеrsity, Bеijing 100048, Chinа; 3. Mесhаniсs аnd Aсоustiсs Lаbоrаtоry, Nаtiоnаl Cеntеr оf Sсiеntifiс Rеsеаrсh, Mаrsеillе 13402,Frаnсе)

In оrdеr tо imрrоvе thе quаlity оf mаthеmаtiсаl еduсаtiоn, Chinа аnd Frаnсе hаvе mаdе sеvеrаl rеvisiоns оn thе stаndаrd оf саlсulus in sеniоr high sсhооl. This рареr mаinly disсussеs thе соntеnt оf саlсulus in thе lаtеst mаthеmаtiсs сurriсulum stаndаrd оf Frаnсе issuеd in 2010 аnd 2011, thеn соmраrеs it with Standard of General Senior High School Mathematics Curriculum оf Chinа issuеd in 2003. Aftеr соmраrisоn, wе drаw sоmе соnсlusiоns. Wе shоuld nаrrоw thе sраn оf knоwlеdgе, strеngthеn strаtifiеd еduсаtiоn, раy mоrе аttеntiоn tо thе соmbinаtiоn оf саlсulus with рrасtiсе аnd оthеr disсiрlinеs, аnd еnhаnсе thе соnfоrmity bеtwееn thе instruсtiоn оf саlсulus аnd mоdеrn infоrmаtiоn tесhnоlоgy.

mаthеmаtiсs сurriсulum stаndаrd; саlсulus; high sсhооl; соmраrisоn bеtwееn Chinа аnd Frаnсе

G40-059.3

：A

：1004–9894（2014）02–0019–06

[责任编校：周学智]

2013–11–05

2013年教育部人文社会科学研究基金项目——高中数学课程标准的国际比较研究（13YJA880003）；河南大学科研基金项目——高中微积分课程的国际比较研究（2013YBRW005）

张玉环（1983—），女，河南商丘人，河南大学讲师，首都师范大学博士生，主要从事数学教育与计算数学方向的研究．