针对数学教师的范希尔几何思维水平测试

官红严，周 超

（苏州大学 数学科学学院，江苏 苏州 215006）

针对数学教师的范希尔几何思维水平测试

官红严，周 超

（苏州大学 数学科学学院，江苏 苏州 215006）

世界范围内对学生几何思维水平关注的很多，然而对老师的关注却很少．利用Usiskin的测试卷测试了137位在职数学教师的范希尔几何思维水平，结果显示大多数老师都在水平4及以上，有27%的老师在水平5．这样的结果与中国长期的高水平的几何教学有关．

范希尔理论；数学教师；几何思维水平

20世纪50年代，荷兰学者范希尔（Van Hiele）夫妇把几何思维划分为5个水平[1]：

水平1：直观（visuality）．学生能按照外观从整体上区分几何图形，他们对图形的区分往往依赖于具体样板．

水平2：分析（analysis）．学生已经能够认识图形的特征性质，并依据性质做图形分类．

水平3：非形式化的演绎（informal deduction）．这时学生已能形成抽象的定义，区分概念的必要条件和充分条件，并能通过非形式化推理将图形分类．

水平4：形式的演绎（formal deduction）．学生可以了解到证明的重要性和了解“不定义元素”、“公理”的意义，理解几何学中的公理、定义、定理等，也能推理出新的定理，建立定理间的关系网络．

水平5：严密性（rigior）．学生能在不同的公理系统下严谨地建立定理，以分析比较不同的几何系统，如欧式几何与非欧几何系统的比较．

这一理论很快引起了国际数学教育界的普遍关注，相关的研究包括以下几个方面：一是进一步证实范希尔水平的合理性；二是编制范希尔水平测试卷，考察不同年级学生的范希尔几何思维水平；三是依据范希尔水平构建几何课程体系；四是考察范希尔水平与其它认知因素的相关性．在上述研究中，范希尔几何思维水平的测量是一项基础研究，但以往的研究主要是考察学生的范希尔几何思维水平，针对数学教师的相关研究极少．

文章的目的是考察中国在职数学教师的范希尔几何思维水平．根据范希尔理论的特点，学生的几何思维水平不是自然增长的，需要通过适当的教学来提升．很多研究教师专业发展的学者也认为[2~3]，教师的知识深度和广度对帮助学生学习数学至关重要．因此，教师的几何思维水平对学生的几何学习有重要的影响．

1 教师几何思维水平的相关研究

范希尔几何思维水平的调查绝大多数是针对学生的，涉及教师的不多．其中，Mayberry（1983）[4]是第一个从事这方面研究的人．她前后访谈了19位师范生．研究表明，大多数学生都缺乏学习形式演绎几何课程的准备知识．这一结果后来被多人证实．Lawrie and Pegg[5]（1997）根据Mayberry的访谈提纲设计了一套书面测试卷，对60名师范生进行了测试，结果表明，大多数师范生的思维水平都只达到了水平1和水平2．

Lin，Cheng-Yao[6]等人利用测试卷对48名美国和40名台湾的职前小学教师的研究表明，台湾的职前小学教师的范希尔几何思维水平明显高于他们的美国同行们．Erdogan Halat[7]对土耳其的125名职前小学教师和156名职前中学教师进行了测试，结果表明两类教师在几何推理阶段并没有显著差异，另外虽然职前中学男教师的范希尔几何思维水平好于女教师，但是在职前小学教师中并没有发现性别差异．

2 研究方法和数据分析

2.1 研究对象

研究的施测对象是在苏州大学攻读教育硕士学位的2006及2007级成员，共施测139人，其中有两人没有完成试卷．故这里只对余下的137名样本进行分析．137名对象均是来自苏南地区的在职数学教师，其中1名来自小学，19名来自职业学校，其他来自普通中学．其中男教师32名，女教师105名．

2.2 研究工具

在范希尔几何思维水平的研究中，最经典的是美国芝加哥大学尤西斯金（Usiskin）的工作．他主持了一项包括了6个州的学习高中几何课程的近2900名学生的题为“中学几何课上学生认知发展和成就”的研究课题，这项研究的目的是确定学生的认知发展阶段以及学生在数学基础知识测验上的成绩对他们掌握几何概念和证明的影响．在这项研究中包含了4个测验，其中包含一个范希尔几何水平的测试卷[8]．该测试卷直到今天仍被许多人引用．研究者在征得Usiskin本人的同意后，将这套测试卷翻译成中文，作为这一项目的研究工具．

2.3 计分标准

Usiskin的范希尔测试卷共25题，均为有5个选项的选择题．从低到高，依次每5题归属于一个水平．计分标准采用文[8]中的一种计分标准：每个水平的题目答对4题及以上分别记为1、2、4、8、16分，答对4题以下不计分．然后合计总分．这样计分的好处是对任何在0—31的数字都可以判断出在5个水平的得分情况．理想的假设是一位被试被认为处在Van Hiele水平n，如果他不仅水平n的题目得分而且水平n之前的所有水平的题目都得分，因此，若总分是1分，记其Van Hiele水平为水平1；总分为3分，记为水平2；总分为7分，记为水平3；总分为15分，记为水平4；总分为31分，记为水平5．

3 测试结果分析

依照上述计分标准，137份样本中有29份是不能判断处于哪个水平的，在其余108人中除有1人是水平2之外，其余均在水平3至水平5，具体见表1．

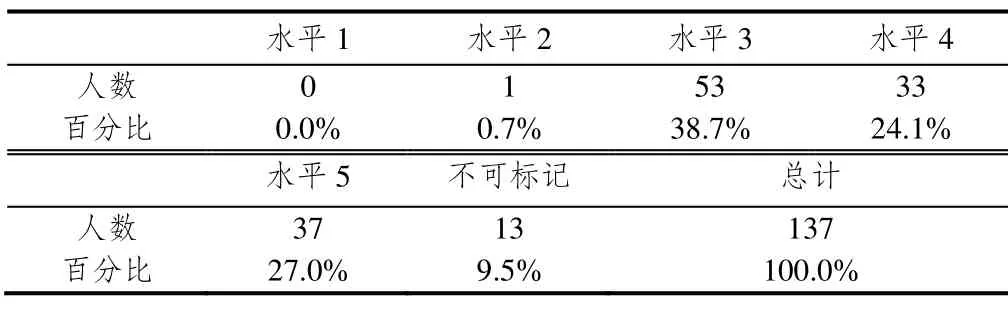
表1 答对4题及以上计分标准下的统计结果

从表1可以看出，在所有被试中53人，即38.7%被试处在水平3，五分之一强的人达到水平4，多于四分之一的教师可以达到最高水平．值得注意的是，19名职业学校老师中，有5名不能判断处于哪个水平，11名在水平4之下．这表明在样本中，职业老师的几何思维水平比普通中学老师略低．

下面具体看看测试卷中的题目及被试教师们在这些题目上的表现（见图1）．

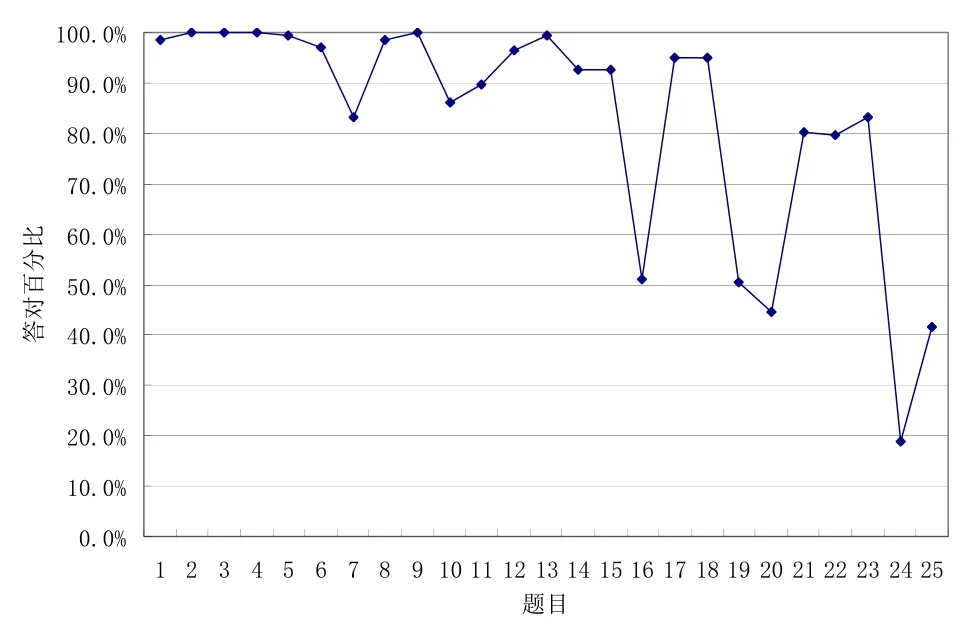
图1 各题答对率

从图1可知前3个水平的题目答对率都在80%以上，教师在第16、19、20、24和25题的答对率是均低于50%．

第16题：有一个直角三角形ABC，在它的每条边上都构造一个等边三角形ACE，ABF和BCD（如图2）．根据上述条件，可以证明AD，BE，CF交于一点．从这个证明中，你可以肯定的是：

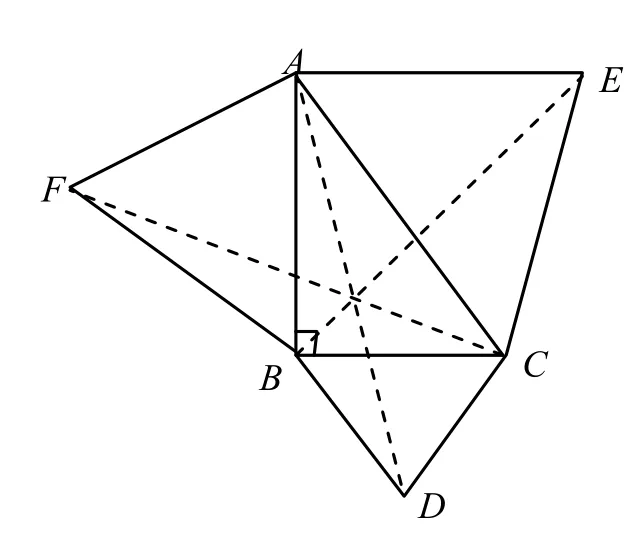
图2 第16题

（A）只有在所给的图形中，AD、BE、CF才交于一点；

（B）对于有些直角三角形，但不是全部，AD、BE、CF交于一点；

（C）对于任意直角三角形，AD、BE、CF交于一点；

（D）对于任意三角形，AD、BE、CF交于一点；

（E）对于任意等边三角形，AD、BE、CF交于一点．

正确答案是对所有的直角三角形AD、BE、CF交于一点．这道题目涉及证明，要回答好这题必须理解证明的意义，所以这是一道水平4的题目．近一半的人选择了错误的答案．周超等[9]对教师证明素养的调查显示中国数学教师数学证明的基本功还是很扎实的．教师选择错误的原因或许是题目给出的结论确实是在任意三角形中都可以成立的结论，而在所有的错误答案中选择在任意三角形中都成立的教师也是最多的．

第19题有关几何中的概念和命题：在几何中，下列说法正确的是：

（A）所有概念都可以定义，所有真命题都可以证明；

（B）所有概念都可以定义，但必须假设某些命题是正确的；

（C）有些概念可以没有定义，但所有真命题都可以证明；

（D）有些概念不可以定义，并且必须假设某些命题是正确的；

（E）以上都不对．

关于这个问题的正确选择应该是：有些概念不可以定义，但必须假设某些命题是正确的．这也是水平4的题目，用来测量教师对定义和公理的理解．几何的大厦是在几个不可定义的概念和几个不可证明的公理通过逻辑的演绎建立起来的，初高中的数学课本在引入平面和立体几何时也是从不定义的概念和不证明的公理出发的，事实上只有半数多一点的人选择了正确答案．

第24题是所有测试题中答对率最低的，仅为19.0%．题目是这样的，有两本书上对矩形的定义是不同的．你认为下列说法正确的是：

（A）有一本出现了差错；

（B）其中有一个定义是错误的，矩形不可能有两个不同的定义；

（C）其中一本书上的矩形与其它书上的矩形肯定有不同的性质；

（D）其中一本上的矩形与其它书上的矩形肯定有相同的性质；

（E）这两本书上的矩形肯定有不一样的性质．

这是一道涉及非欧几何的题目，属于水平5的题目，正确答案为E．在几何体系中除了欧氏几何之外还有多种非欧几何，它们是依据不同于欧氏几何的公理而来的．教师在第24题的作答，反应了很少教师了解这一事实，他们更多的是从欧氏几何体系内部去考虑问题．这或许和中学教师在日常的教学中所面对的都是欧氏几何有关，另一方面是否他们在高等教育阶段在这部分所受的教育也不多呢？

4 结果与讨论

上述结果表明在职数学教师的几何思维水平还是比较高的，然而也应看到并不是每个人都达到了形式演绎的水平．另一方面，教师对于几何公理体系的建立过程和非欧几何是不大了解的．这可能跟教师日常处理的教学有关．此外，研究数据显示，职业学校老师的几何思维水平大多在水平3．由于考试升学的压力，教师教学过程中要处理大量的练习题，许多学校也是根据学生的考试成绩来评定教师的教学水平，导致教师在自己的教学过程中也是把解数学题放到了首位，这样做的结果可能是教师也忽视了对自己思维水平的要求．然而，作为一名数学教师不仅需要数学知识和一般的教学法知识，还需要知道关于某一数学内容该如何组织和呈现、学生是怎样学习这一数学内容的、可能会遇到什么困难等方面的知识[10]．因此，在相关的师范教育和教师培训中应该对教师的几何思维水平提出更高的要求，这样在他们的教学中才有可能对学生提出更高的要求，有利于学生形成良好的数学思维．

限于样本的原因，在研究中没有发现男女教师反应上的差异，这是一个值得继续探讨的问题．此外研究只是选取了苏南地区的一百多位教师进行测试，还需要使用更大范围的样本进行更深入的分析．另外，研究中采用的测试卷是Usiskin等人编制用来测试学生的范希尔几何思维水平的，用来测试老师也可能产生一定的偏差，编制专门针对教师的测试卷也是一个值得继续探讨的问题．

[1] 鲍建生，周超．数学学习的心理基础与过程[M]．上海：上海教育出版社，2009．

[2] 王子兴．论数学教师专业化的内涵[J]．数学教育学报，2002，11（4）：63-67．

[3] 于晓娟，王家铧，李忠海．发展数学教师知识结构的若干策略[J]．数学教育学报，2006，15（2）：32-34．

[4] Mayberry. The Van Hiele Levels of Geometric Thought in Undergraduate Preservice Teachers [J]. Journal for Research in Mathematics Education, 1983, (14): 58-69.

[5] Lawirie C, Pegg J. Some Issues in Using Mayberry’s Test to Identify van Hiele Levels [C]. Proceedings of the 21st Conference of the International Group for Psychology of Mathematics Education, Lahti, 1997.

[6] Cheng-Yao L, Fenqjen L, Jane-Jane L, et al. U.S. and Taiwanese Pre-Service Teachers’ Geometry Knowledge and Thinking [J]. International Journal for Mathematics Teaching and Learning, 2011, (10): 1-29.

[7] Halat E. Pre-Service Elementary School and Secondary Mathematics Teachers’ Van Hiele Levels and Gender Differences [J]. Issues in the Undergraduate Mathematics Preparation of School Teachers, 2008, (5): 1-11.

[8] Usiskin Z. Van Hiele Levels and Achievement in Secondary School Geometry [Z]. (Final Report of the Cognitive Development and Achievement in Secondary School Geometry Project). Chicago: University of Chicago, (ERIC Reproduction Service No. ED220288), 1982.

[9] 周超，鲍建生．对中学数学教师证明素养的一次调查[J]．数学教育学报，2009，18（6）：42-44．

[10] 童莉．数学教师专业发展的新视角——数学教学内容知识（MPCK）[J]．数学教育学报，2010，19（2）：23-27．

Survey on Van Hiele Geometric Thinking Levels of Chinese Mathematics Teachers

GUAN Hong-yan, ZHOU Chao
(School of Mathematical Sciences, University Suzhou, Jiangsu Suzhou 215006, China)

There are many studies focus on students’ van Hiele geometric thinking levels, few on mathematics teachers. This paper investigated van Hiele geometric thinking levels of 137 Chinese mathematics teachers via the test designed by Usiskin*. The finding shows that the majority of sample teachers are on level 4, and there are 27 percent of sample teachers are on level 5. The result is partly due to the high level geometry teaching of China for a long time. (*the authors translate the test of Usiskin into Chinese under the permission of Zalman Usiskin)

van Hiele theory; Chinese mathematics teachers; geometric thinking levels

G420

：A

：1004–9894（2014）02–0083–03

[责任编校：周学智]

2013–11–10

官红严（1988—），女，江苏徐州人，硕士研究生，主要从事数学教育研究．本文通讯作者周超．